|
|
BMe Kutatói pályázat |
|
Pattantyús-Ábrahám Géza Gépészeti Tudományok Doktori Iskola
BME Gépészmérnöki Kar, Műszaki Mechanikai Tanszék
Témavezető: Dr. Dombóvári Zoltán
Általános geometriájú üregelő megmunkálások dinamikus szimulációja
A kutatási téma néhány soros bemutatása
Az üregelést mint az egyik legpontosabb és legrobusztusabb forgácsolási eljárást, előszeretettel alkalmazza számos magas elvárásokat támasztó iparág, mint például a repülőgép- és autógyártók, vagy az energiaszektor. Ez a folyamat kivételesen hatékony bonyolult geometriájú furatok kialakításában, nagy pontosság és kiváló felületi minőség mellett. Bár széles körben alkalmazzák, a forgácsolási folyamat dinamikája nagyon kevéssé ismert. A kutatásom fő célja ezen hiány pótlása és a művelet viselkedésének mélyebb megértése volt, amelyhez egy összetett, részletekbe menő dinamikus szimulációs keretrendszert dolgoztam ki. Az általam fejlesztett algoritmusok segítséget tudnak nyújtani az üregelési folyamatok tervezésében, monitorozásában és optimalizációjában, ami növeli a művelet hatékonyságát és termelékenységét.
A kutatóhely rövid bemutatása
Doktori képzésem során a kutatómunkám egy jelentős részét az MTA-BME Lendület Szerszámgéprezgések Kutatócsoport keretein belül végeztem, a BME-GPK Műszaki Mechanikai Tanszékén. Az üregelési folyamatokat modellező szimulációs környezet fejlesztését elsősorban az InterQ Európai Uniós kutatói konzorciumban való részvételünk motiválta.
A kutatás történetének, tágabb kontextusának bemutatása
Az üregelési folyamatokat modellező szimulációs környezet fejlesztésébe eredetileg az InterQ konzorcium egyik tagja, egyben a repülőgépipar egy jelentős szereplője, az ITP Aero felkeresésére kezdtünk. Mint sokan mások, ők is üregelő megmunkálások segítségével hozzák létre a repülőgép-hajtóművekben található turbinalapátok rögzítésére szolgáló karácsonyfa alakú hornyokat. Ezeknek a bonyolult furatgeometriáknak rendkívül magas méretpontossági és felületi minőségi elvárásoknak kell megfelelniük. A selejtes munkadarabok elkerüléséhez elengedhetetlen a forgácsolási folyamat dinamikájának mélyreható ismerete.
Az esztergáláshoz és a maráshoz hasonlóan, az üregelő megmunkálások során is megjelenhetnek káros, öngerjesztett rezgések, amelyeket a jellegzetes hangjuk után „chatter”-nek szokás nevezni [1,2]. Mindezek ellenére az üregelési műveletek dinamikája rendkívül gyengén kutatott. Ennek egyfelől a modellezési folyamat bonyolultsága, másfelől pedig a szerszámgépgyártók által alkalmazott adatvédelem az oka. A témában született legtöbb tanulmány vagy a forgácsoló erők statikus becslésével foglalkozik a szerszámgép dinamikájának figyelembe vétele nélkül, vagy teljesen empirikus módszerekre alapozva monitorozza a folyamat magasabb szintű jellemzőit, mint például a szerszámkopást vagy a munkadarab felületi minőségét. Ezen felül számos kutatásban használnak végeselemes szimulációkat a művelet bizonyos aspektusainak modellezéséhez. Habár ez a megközelítés lehetőséget nyújt tranziens, dinamikus szimulációk futtatására is, a rendkívül magas számítási kapacitás igény, lehetetlenné teszi a mélyreható dinamikai analízist.
A kutatás célja, a megválaszolandó kérdések
A kutatásom elsődleges célja egy gyors és hatékony, de ugyanakkor pontos és megbízható dinamikus szimulációs környezet fejlesztése volt üregelő megmunkálásokhoz. Az ipari partnereink igényeit végig szem előtt tartva funkciók széles skáláját építettük be a szoftvercsomagba [S2]. Jelenlegi állapotában a szimulációs környezet lehetővé teszi:
- Általános vágóél-geometriák pontos, automatikus és robusztus diszkretizációját.
- A forgácsvastagság dinamikus számítását vágóélkilépések figyelembe vétele mellett. [S1]
- A forgácsolás során várható erők gyors és megbízható becslését ortogonális forgácsolás segítségével illesztett erőkarakterisztikák alapján.
- A szerszámgép-dinamika leírását modális paraméterillesztés nélkül az impulzusválasz-függvények terében (IDS) [3].
- Munkadarab-felületek automatikus generálását a vágóélek pályájának követésén keresztül.
- A szimulációs eredmények sokrétű feldolgozását és vizualizációját, mint például virtuális felületi érdesség mérések elvégzését.
A fejlesztett szimulációs környezet segítségével lehetőségünk nyílt részletes numerikus tanulmányokat folytatni az üregelő megmunkálások dinamikai viselkedéséről. Mivel ezen folyamatok általában rövidek, és a megmunkálást végző fogak száma alacsony, nehéz megfelelő stabilitásdefiníciót találni. Ennek ellenére megéri tranziens dinamikai viselkedéseket elemezni, és definíciót találni a véges idejű stabilitásra a káros “chatter” rezgések azonosítása és elkerülése érdekében.
Módszerek
A legfontosabb újdonság a szimulációs környezetünkben egy újszerű modellezési megközelítés, amely a fellelhető folytonos végeselemes modellek helyett egy koncentrált paraméterű késleltetett differenciálegyenlet segítségével írja le az üregelő megmunkálás dinamikáját. Ha magát az üregelő szerszámot végtelenül merevnek, az üregelést végző szerszámgépet pedig mindhárom transzlációs irányban deformálhatónak tételezzük fel (1.(a) ábra), a folyamat modellezhető egy háromdimenziós mechanikai rendszerként. A szabadsági fokok számát és a rendszert leíró differenciálegyenlet dimenzióját pedig a szerszámgépdinamika leírásához felhasznált módusok száma fogja meghatározni. Ezek előállíthatók impulzuskalapáccsal végzett modális mérések alapján, hagyományos paraméterillesztés [4] vagy IDS-alapú direkt reprezentáció segítségével [3].
Általános vágóél- és furatgeometriákat feltételezve a modellezési folyamat legnehezebb része a forgácsoló erők pontos leírása. Jelen esetben ezt a problémát az élek diszkretizációján keresztül oldottuk meg (1.(b) ábra). A szimulációs környezet minden egyes élszegmens esetében számon tartja a dinamikus forgácsvastagságot, és azt, hogy az elem éppen a munkadarabban található-e. Mért forgácsolási erőkarakterisztikák alapján (1.(c) ábra) minden elem esetében meghatározza a lokális forgácsolási erő komponenseit, majd ezeket összegezve állítja elő a globális forgácsoló erőt. Megengedve a vágóélek kilépését [S2], az aktív forgácsvastagság számításához nyomon kell követni az összes megelőző vágóél munkadarabon hagyott nyomát (1.(d) ábra). A forgácsoló erő ezen múltbéli pályáktól való függése okozza az úgynevezett regeneratív hatást, és ennek következtében – jelen esetben a szerszám szabad axiális elmozdulása és a forgácsolási sebesség megengedett ingadozásai miatt – állapotfüggő késések jelennek meg a rendszert leíró mozgásegyenletben.
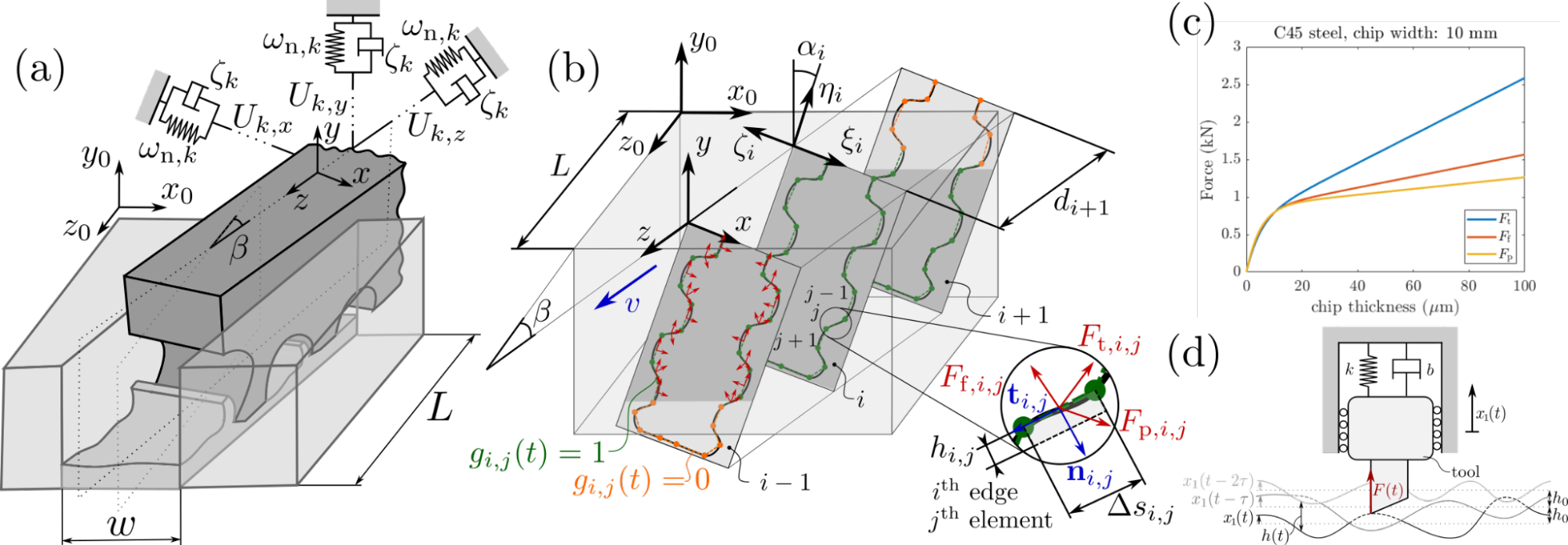
1. ábra Üregelő megmunkálások dinamikus szimulációs modellje.
Egy ilyen rendkívül bonyolult mechanikai rendszer hatékony szimulációja érdekében problémaspecifikus integráló algoritmusokat kellett fejlesztenünk. Ezen felül – az ipari partnereink igényeit kielégítendő – számos adatfeldolgozó és vizualizációs funkciót is meg kellett valósítanunk. Ezek közül csak párat kiemelve: létrehoztunk algoritmusokat statikus és kvázi-statikus forgácsoló erők számításához, munkadarab-felület automatikus generálásához és virtuális felületi érdesség mérések elvégzéséhez.
Eddigi eredmények
Egy mintaszimuláció eredményei láthatók a 2. ábrán. Ahogy azt az (a) panel is demonstrálja, az üregelő szerszám megfelelő diszkrét reprezentációja elengedhetetlen előfeltétele ilyen szimulációk futtatásának. Ez nemcsak az egyes élszegmensek pozíciójának és méretének leírását foglalja magában, hanem az ezekhez tartozó normálvektorok és előírt forgácsvastagság-értékek meghatározását is. Ennek a diszkretizációs folyamatnak a megkönnyítése érdekében automatikus, képfelismerésen alapuló segítő algoritmusokat is fejlesztettünk. Egy ilyen diszkretizált geometria, a szerszámgépdinamika egy modális paraméterillesztés vagy IDS-alapú leírása, és egy a munkadarab anyagához tartozó empirikus forgácsoló erőkarakterisztika alapján a szimulációs környezetünk képes a (b) panelen látható elmozdulás- és erőjelek előállítására. Ez a folyamat a diszkretizáció felbontásától függően általában néhány másodpercig vagy percig tart, ami több nagyságrenddel gyorsabb, mint egy tranziens végeselemes szimuláció futtatása lenne.
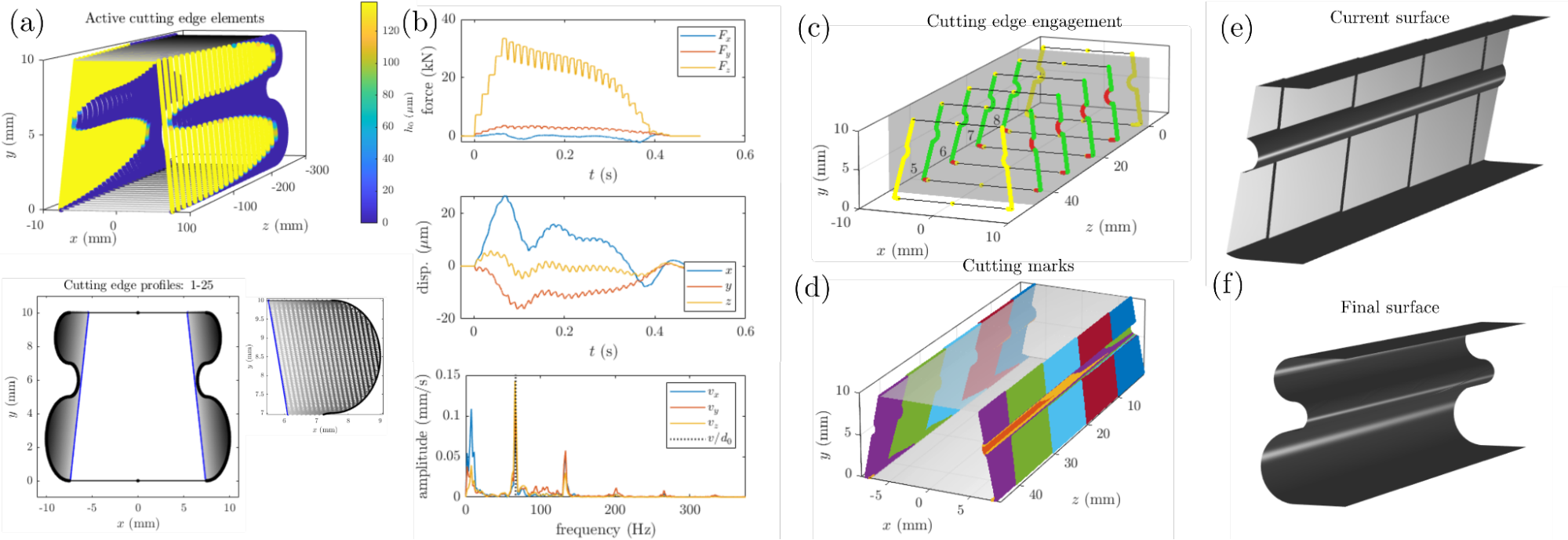
2. ábra Üregelési folyamat dinamikus szimulációjának eredményei.
Ahogy azt a 2. ábra (c-f) paneljei is mutatják, az általunk fejlesztett posztprocesszáló algoritmusok lehetővé teszik a vágóélelemek aktivitásának és a munkadarab-felület alakulásának online nyomon követését. A (c) panelen sárga pontok jelölik a munkadarab befoglaló hasábján kívül eső, piros pontok a munkadarabból kilépett és zöld pontok az aktívan forgácsoló élszegmenseket. A (d) panelen a különböző színek az egyes vágóélek által hagyott nyomokat különböztetik meg.
A szimulációs környezetünk felhasználási lehetőségeit legjobban talán az alábbi bemutató videó tudja szemléltetni:
3. ábra Szimulációs környezet bemutató videója.
A kész szimulációs algoritmusaink segítségével lehetőségünk volt mélyreható numerikus tanulmányokat folytatni az üregelő megmunkálások dinamikai viselkedéséről. A tranziens időjelek hatékony szimulációja lehetővé tette megbízható véges idejű stabilitási mérőszámok meghatározását. Ezeken keresztül optimalizálni tudtuk a forgácsolási folyamat bizonyos aspektusait, például az üregelő szerszám axiális fogkiosztását. A fogközök variálásának pozitív hatásait és az így elérhető robusztusság-növekedést a 4. ábra demonstrálja.
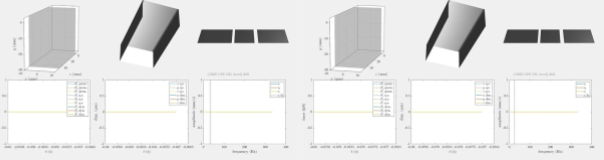
4. ábra Egy instabil egyenletes és egy stabil váltakozó fogkiosztású üregelő folyamat összehasonlítása.
Várható impakt, további kutatás
A szimulációs környezet jelenlegi állapotában jól használható valódi ipari üregelési folyamatok virtuális ikertestvéreként. Nemcsak a forgácsolás során fellépő erőket tudja pontosan előrejelezni, de a munkadarab várható felületi minőségét és pontosságát is képes becsülni. Segítségével részben kiválthatók az időigényes és rendkívül drága forgácsolási tesztek például új szerszámgeometriák vagy munkadarab-alapanyagok kiválasztása során.
A jövőben
szeretnénk kiterjeszteni a szimulációs algoritmusainkat, hogy segítségükkel
modellezhető legyen a vágóélek kopása, a szerszámgépek paraméter- és időfüggő
dinamikája [S3], és egyes aktívan kontrollált aktuátorok hatása [S4]. Mindezen
felül, a felhasználói élmény javítása érdekében aktívan dolgozunk az
automatikus élfelismerő és diszkretizáló algoritmusainkon.
Saját publikációk, hivatkozások, linkgyűjtemény
Kapcsolódó saját publikációk listája
[S1] Iklodi, Z., Gabos, Z., Bártfai, A., & Dombovari, Z. (2023). Time Domain Simulation of Surface Topography in Broaching Considering Tools with General Cutting-Edge Geometries and Three DoF Parametric Dynamics. Advances in Science and Technology, 132, 3–12. DOI
[S2] Iklodi, Z., Barton, D. A., & Dombovari, Z. (2022). Bi stability induced by motion limiting constraints on boring bar-tuned mass dampers. Journal of Sound and Vibration, 517, 116538. DOI
[S3] Iklódi, Z., Beudaert, X., & Dombovari, Z. (2022, August). On the modelling bases of in-motion dynamic characterization of flexible structures subject to friction and position control delay. In International Design Engineering Technical Conferences and Computers and Information in Engineering Conference (Vol. 86311, p. V010T10A024). American Society of Mechanical Engineers. DOI
[S4] Iklódi, Z., Astarloa, A., & Dombovari, Z. (2019). Vibration Attenuation of Boring Bars with Nonlinear Control Force. MM Science Journal, 3086–3092. DOI
Linkgyűjtemény
● ITP Aero - turbine engine case study
Hivatkozások listája
[1] Quintana, G., & Ciurana, J. (2011). Chatter in machining processes: A review. International Journal of Machine Tools and Manufacture, 51(5), 363–376. DOI
[2] Axinte, D. A. (2007). An experimental analysis of damped coupled vibrations in broaching. International Journal of Machine Tools and Manufacture, 47(14), 2182–2188. DOI
[3] Dombovari, Z. (2021). Stability properties of regenerative cutting processes, based on impulse response functions expressed in the impulse dynamic subspace. International Journal of Machine Tools and Manufacture, 162, 103691. DOI
[4] Ewins, D. J. (2009). Modal testing: theory, practice, and application. John Wiley & Sons.
