Géza Pattantyús-Ábrahám Doctoral School of Mechanical Engineering 

BME GPK, Department of Applied Mechanics

Supervisor: Dr. Dombóvári Zoltán

Dynamic simulation of broaching operations considering general cutting-edge geometries

Introducing the research area

Being one of the most accurate and reliable metal-cutting operations, broaching is used extensively by demanding industrial sectors such as the automotive, aeronautics, and energy industries. It is exceptionally potent at manufacturing bores of intricate geometries with high dimensional accuracy and surface integrity. Despite its widespread use, the dynamics of this cutting process is very poorly understood. The main goal of my research was to help bridge this gap through the development of an in-depth dynamic simulation framework, which may aid process planning, monitoring, and optimization, to lower scrap production, and energy consumption and facilitate productivity.

Brief introduction of the research place

During my PhD, I conducted most of my research within the framework of the MTA-BME Lendület Machine Tool Vibration Research Group, at the Department of Applied Mechanics of BME-GPK. The simulation framework we developed for broaching operations was motivated by our participation in the InterQ research consortium of the European Union.

History and context of the research

The need for fast and reliable dynamic simulation of broaching came from ITP Aero, a participant in InterQ, and a major player in the aerospace industry. As with many others, they use broaching to manufacture the complex Christmas-tree-shaped bores of turbine discs that house the turbine blades of aircraft jet engines. Naturally, these intricate bore geometries must meet exceptionally high accuracy and surface quality requirements, and in-depth knowledge of the corresponding manufacturing process dynamics is essential for avoiding scrap parts.

Just like other conventional metal cutting operations, such as milling and turning, broaching is prone to exhibit harmful self-excited vibrations, also known as chatter by the machining community [1,2]. Nevertheless, the dynamic behavior of this cutting process is very scarcely researched. This is on one hand due to the difficulty of process modeling and to the manufacturers’ unwillingness to disclose design specifications on the other. Most studies concerning broaching either focus on the static or quasi-static estimation of cutting forces without taking machine tool dynamics into account or rely solely on empirical methods to monitor more abstract aspects of the process, such as tool wear and/or workpiece surface integrity. There are several studies, that employ finite element techniques to simulate certain aspects of broaching processes, however, due to the extremely high computational costs associated, this approach is inherently unfit for in-depth dynamical analysis.

The research goals, open questions

The primary goal of my research was the development of a fast and computationally efficient, yet accurate and reliable dynamic simulation framework for broaching processes. Keeping the needs of our industrial partners in mind, we developed a wide range of functionalities, which previously have been unavailable. In its current state of development, our simulation framework [S1] allows:

1. Automated, accurate, and robust discrete representation of general, often highly intricate innovative geometries.
2. Automatic calculation of the dynamic chip area accounting for possible cutting-edge contact loss and fly-over events [S2].
3. Fast and reliable estimation of dynamic cutting forces based on widely available orthogonal cutting data.
4. Description of broaching machine dynamics in a data-driven, modal parameter-free framework, using an impulse dynamics subspace (IDS) representation [3].
5. Automatic generation of the workpiece surface, by tracking the path of all cutting edges.
6. A wide range of visualization and post-processing options, e.g., a virtual surface roughness measurement scheme.

With the help of our simulation engine, we also set out to conduct an in-depth numerical study of broaching operations. Since generally it is a very short operation, only a couple of seconds long, it is hard to define an adequate stability measure. Nevertheless, for the identification and prevention of harmful chatter vibrations, it is worthwhile to study transient trajectories and define finite time stability identifiers.

Methods

The main novelty of our dynamic simulation framework is a new approach to modeling broaching operations. Contrary to previous finite element-based continuous representations, here we use a lumped parameter and delay differential equation-based description. Making a few key assumptions, such as considering a completely rigid broaching tool, and a broaching machine, which is compliant in all three translational directions (Figure 1. (a)) the operation can be described by a three-dimensional dynamical system. Meanwhile, the number of degrees of freedom and the actual dimension of the governing equation of motion will depend on the number of vibratory modes considered. The characterization of these modes can be done based on impulse response functions obtained via impact hammer tests, using conventional modal parameter fitting [4] or a novel IDS-based direct representation [3].

Considering general innovative geometries, the most difficult part of modeling broaching operations is the accurate description of the cutting forces. Here we take a discretization-based approach, where we calculate cutting forces in an element-by-element manner (Figure 1.(b)). To do so, the simulation framework keeps track of which elements are currently in contact and determines the dynamic chip thickness of all active elements automatically. Then local force components are evaluated using an empirical cutting force model (Figure 1.(c)) and are summed up over all elements of all cutting edges to arrive at the global cutting force. Considering the possibility of a cutting edge exiting the workpiece due to tool vibrations [S2], the evaluation of the active chip thickness requires keeping track of all the marks left on the workpiece by previous cutting edges (Figure 1. (d)). This dependence of the cutting force on past trajectories introduces a regenerative effect, which due to the allowed axial displacements and consequent deviations of the cutting speed, leads to the emergence of state-dependent delays in the governing equation of motion.

 

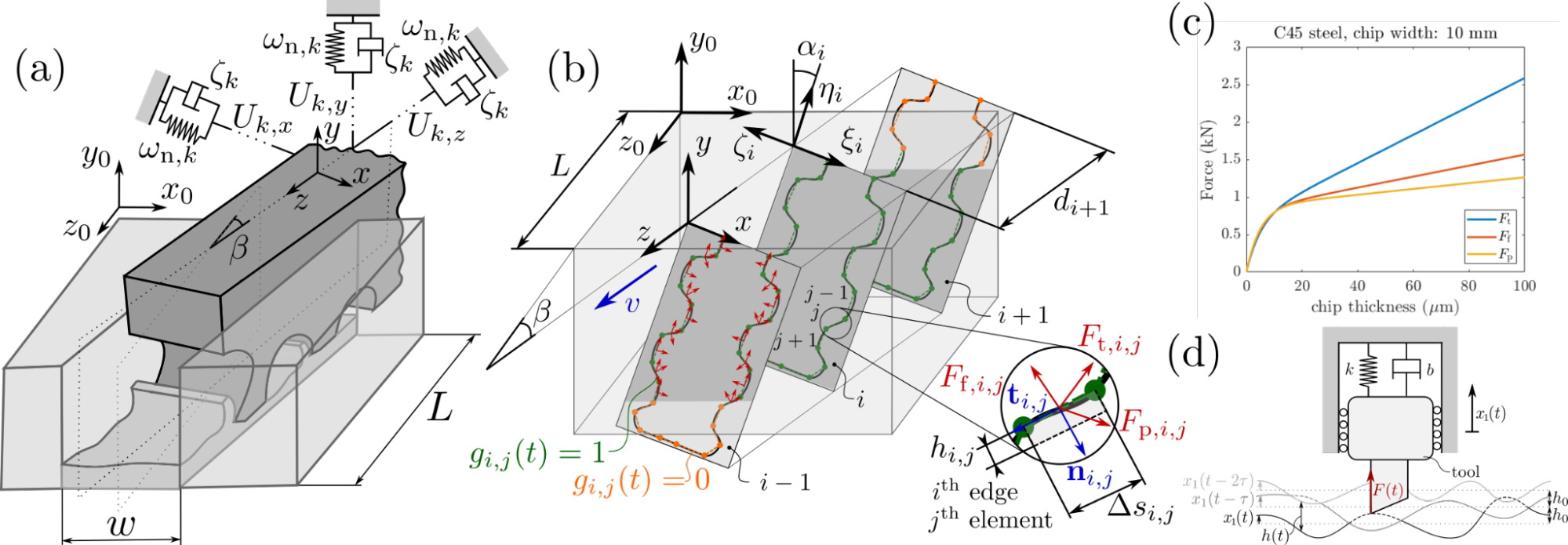
Figure 1. Dynamic simulation model of the broaching process.

 

To efficiently simulate the resulting highly intricate dynamical model of broaching, we had to develop problem-specific integrator algorithms. Furthermore, to meet the needs of our industrial partners, we also developed a wide range of post-processing functionalities. These included the evaluation of static and quasi-static cutting forces, the automatic generation of workpiece surfaces, a tool for conducting virtual surface roughness measurements, and a plethora of visualization options.

Results

Outputs of an example simulation run are presented in Figure 2. As illustrated by the panel (a), the prerequisite for conducting such a simulation is an adequate discrete representation of the broaching tool geometry. This includes identifying not only the length and position of each element but also the corresponding edge normals and prescribed feed values. To help facilitate this discretization process we have also developed automatic image recognition-based tools. Using this discretized geometry, an adequate modal parameter or IDS-based description of the machine dynamics, and cutting force data of the workpiece material, the simulation framework can produce force and displacement signals, such as the ones seen in panel (b). Depending on the resolution of discretization this process is completed in a matter of seconds or minutes. This is several orders of magnitude faster than running full-scale transient finite element simulations would be.

 

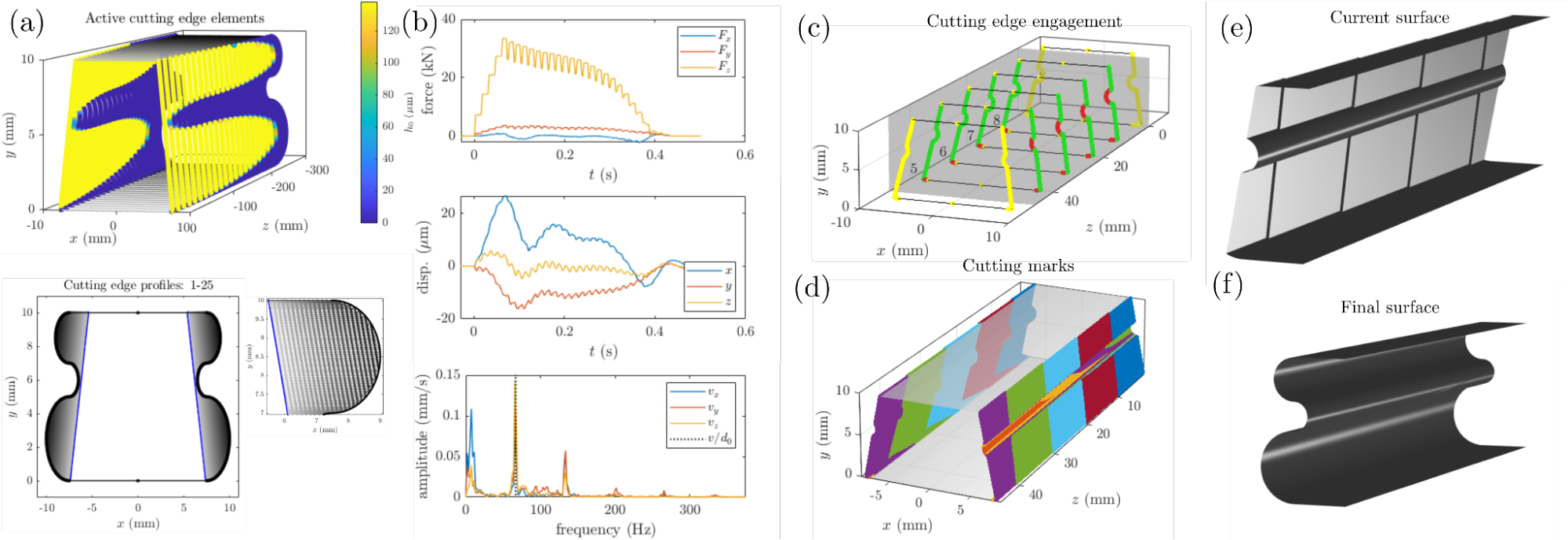
Figure 2. Dynamic broaching simulation results.

 

As illustrated by panels (c) to (f) of Figure 2., the post-processing tools we have developed within our simulation framework, also allow the visualization of online cutting-edge element engagement and workpiece surface evolution. On panel (c) elements marked with yellow are outside the workpiece, elements marked with red are currently exiting, and elements marked with green are actively cutting. On panel (d) different colors are used for marks left by different cutting edges of the broaching tool.

The use of our simulation framework is best demonstrated by the following instructional video we have produced:

 

Figure 3. Demonstration of the simulation framework.

 

With the help of our completed simulation framework, we were able to conduct in-depth numerical studies on the dynamic behavior of broaching processes. Efficient simulation of transient behaviors allowed us to define reliable finite-time stability measures, through which we were able to optimize certain aspects of the operation. One of these avenues was the optimization of the axial, tooth distribution. The beneficial effects of modifying the distances between subsequent cutting edges is demonstrated in Figure 4.

 

Figure 4. Comparison of unstable uniform pitch and stable variable pitch broaching operations.

Expected impact and further research

The simulation framework in its current state works well as a digital twin for actual industrial broaching processes. It can provide reliable predictions for the cutting force loads and it can also estimate workpiece surface integrity and accuracy. It may be used to partially replace expensive and time-consuming cutting tests, with e.g. new materials or broaching tool geometries.

In the future, we aim to expand our simulation model, to account for tool wear, time-varying or operation parameter-dependent machine tool dynamics [S3], and active control intervention [S4]. To make our framework more accessible, we are also actively improving our automatic innovative geometry detection and discretization algorithms.

 

 

Publications, references, links

List of corresponding own publications:

[S1] Iklodi, Z., Gabos, Z., Bártfai, A., & Dombovari, Z. (2023). Time Domain Simulation of Surface Topography in Broaching Considering Tools with General Cutting-Edge Geometries and Three DoF Parametric Dynamics. Advances in Science and Technology, 132, 3–12. DOI

[S2]Iklodi, Z., Barton, D. A., & Dombovari, Z. (2022). Bi-stability induced by motion limiting constraints on boring bar-tuned mass dampers. Journal of Sound and Vibration, 517, 116538. DOI

[S3] Iklódi, Z., Beudaert, X., & Dombovari, Z. (2022, August). On the modelling bases of in-motion dynamic characterization of flexible structures subject to friction and position control delay. In International Design Engineering Technical Conferences and Computers and Information in Engineering Conference (Vol. 86311, p. V010T10A024). American Society of Mechanical Engineers. DOI

[S4] Iklódi, Z., Astarloa, A., & Dombovari, Z. (2019). Vibration Attenuation of Boring Bars with Nonlinear Control Force. MM Science Journal, 3086–3092. DOI

 

Table of links:

●     ITP Aero - turbine engine case study

●     InterQ - BME participation

 

List of references:

[1]    Quintana, G., & Ciurana, J. (2011). Chatter in machining processes: A review. International Journal of Machine Tools and Manufacture, 51(5), 363–376. DOI

[2]    Axinte, D. A. (2007). An experimental analysis of damped coupled vibrations in broaching. International Journal of Machine Tools and Manufacture, 47(14), 2182–2188. DOI

[3]    Dombovari, Z. (2021). Stability properties of regenerative cutting processes, based on impulse response functions expressed in the impulse dynamic subspace. International Journal of Machine Tools and Manufacture, 162, 103691. DOI

[4]    Ewins, D. J. (2009). Modal testing: theory, practice and application. John Wiley & Sons.