|
|
BMe Research Grant |
|
Géza Pattantyús-Ábrahám Doctoral School of Mechanical Engineering
BME GPK, Department of Energy Engineering
Suervisor: Dr. KOVÁCS Róbert Sándor
Beyond Fourier thermal conductivity in complex materials
Introducing the research area
Engineering practice uses a wide range of complex materials – such as various foams and composites – for which there is no reliable thermal modelling background. Still, it is important to determine their thermal properties. This requires the development of a new general methodology that can be applied to any heterogeneous material. My task is to develop this methodology, to put it into practice, and to facilitate its everyday use.
Brief introduction of the research place
The Department of Energy Engineering has a long tradition of research on heat conduction, in which the work of László Kiss, Gyula Gróf, and Tamás Környey has played an outstanding role. At present, the Irreversible Thermodynamics Research Group is involved in heat conduction research at the Department, and I am participating in the activities of this group.
History and context of the research
In all fields of engineering, it is essential to know the physical properties of the materials one is working with, and the required data are not always available and should be determined by laboratory measurements. However, having the experiments done, a suitable model (and adequate knowledge) is required to evaluate raw data. The existing models may have an inadequate range of validity, but in the absence of an alternative, we are content with knowing the error-laden values. In such cases, thermodynamics is of paramount importance in modelling material behaviour, as it can be used to extend the range of validity of existing thermal conductivity models.

Figure 1. Rocks [S11], concrete and metal foam samples [S7].
Thanks to modern manufacturing technologies, engineering applications have introduced materials and material structures that cannot necessarily be described with the classical Fourier law with the desired accuracy, and thus the thermal properties of a given material cannot be properly predicted [2].
In my research, I study samples from completely different areas, whose composition cannot be modelled properly, because there is a lot of heterogeneity in their structure, such as fractures, cracks, and porosities. Such samples include metal foams of different compositions, carbon foams, rocks from drillings, and various refractory insulating materials. The basic motivation for this research is to find answers to the question of how to thermally characterise materials with complex structures, thus helping all engineering disciplines to work with accurate material parameters, thus reducing the number of defects found.
Figure 2. Insulation, printed circuit boards [S14, S9], carbon foam [S6] and graphene oxide samples [S10]
The research goals, open questions
In the course of our work, we receive many requests from the industry to verify the difference between a theoretical estimate and real temperature data, and to prove the accuracy or otherwise of their thermal parameters. This is not a unique case, but in the absence of appropriate descriptive equations, the physical parameters of a material under investigation are not always correct, which can lead to larger temperature deviations compared to calculated or even modelled cases.
In the course of the research, we seek to answer questions such as how the existence of heterogeneities affects thermal conductivity, what effect they have, and how the thermal diffusivity of a material, and hence its thermal parameters, can be estimated in the case where the Fourier equation does not give a suitable solution.
The effective modelling used does not rely on knowledge of the exact material structure, so Fourier's law works, making the model more widely and efficiently applicable. In this research, I examine materials that are relevant to practice. This requires improvements in the methodology of evaluating experiments using models other than Fourier. In addition, the design of another type of experiment is under planning, in which the number of heat pulses and their length can be programmed, thus deepening our understanding and knowledge of the heat conduction phenomenon.
Methods
The heat pulse experiment
The thermal diffusivity can be determined by a simple experiment called the heat pulse experiment [1]. The main devices of the apparatus are a flash lamp, which induces a heat flux, and a thermocouple, which measures temperature. A sample holder to hold the material is placed between the lamp and the thermocouple. The experiment is performed by exciting the inserted sample with a 0.01-second heat pulse, the effect of which is read out by the thermocouple, which provides an electrical signal, and the data is digitized using a PC oscilloscope. Since the experimental setup is closed, the occurrence of a flash is indicated by a photovoltaic sensor located next to the sample holder. Following the processing of the raw data, a unified Fourier and non-Fourier model evaluation methodology is required to process the experimental data [S1].



Figure 3. Heat pulse device and schematic diagram [S4].
Used models, experimental evaluation
The first step in the experimental evaluation is the Fourier equation, followed by two alternative heat conduction models, the Guyer-Krumhansl equation [3] and the Jeffreys equation [S8]. The evaluations are based on an iterative procedure based on a sensitivity analysis. The evaluation of several hundred different measurements allows us to compare the deviation of the heterogeneity of the different types of samples from the temperature curve calculated by the classical Fourier equation, and thus the error that the calculation without using the alternative heat conduction equations can give.

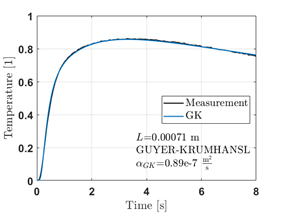
Figure 4. Evaluation of samples with Fourier and alternative heat conduction equations.
By using the Guyer-Krumhansl equation, the extra parameters in the equation can be used to calculate the effective thermal diffusivity of the Fourier equation, which is an average time scale of the parameters obtained, thus predicting the transient behaviour of the samples and materials under investigation.
Results
Analysis of samples
In my research, I have investigated several samples of different compositions and sources, including rocks, metal foams, carbon foams, printed circuit boards, insulations, and reduced graphene oxide composites [S6, S7, S9-12, S14]. These materials have a wide range of practical applications, so the scope of the research's practical use is clearly visible and tangible. Having already performed thousands of measurements on the samples, we have sufficient raw data to properly investigate the thermal behaviour of materials with heterogeneities.
Development of an evaluation methodology
For the experiment, in addition to the Fourier equation, a suitable evaluation methodology has been constructed for the Guyer-Krumhansl and Jeffreys equations, and an iterative procedure based on sensitivity functions has been developed to determine the unknown parameters of the model. Using the Guyer-Krumhansl equation, a relationship can be seen with the Fourier equation, so a simple relationship can be used to link the two models. From these, the thermal diffusivity used in the Fourier equation can be derived from the alternative model. Thus it can be said that the Fourier equation can be applied to non-Fourier materials, but only in a limited way. Hence, thermal modelling of heterogeneous materials does not require accurate modelling of the structure and hence the use of supercomputers and extremely energy-intensive computational capacity.
Expected impact and further research
Based on the research carried out so far, it can be stated that we can offer a tool for engineering practice to more easily and accurately determine the thermal properties of materials with heterogeneous structures. The research and the methodology developed can answer the question of how to model complex structures with intricate material structures and how to incorporate them into a finite element environment by determining thermal parameters, which is expected to have a major impact on all areas of engineering practice.
For further testing and heat pulse experiments, a second lamp is also available, which does not flash once but can be programmed to apply multiple heat pulses to the inserted sample. This allows testing the sensitivity of models and evaluation methodologies to the presence of multiple and different boundary conditions.
Publications, references, links
List of related own publications.
[S1] Fehér A., Lukács N., Somlai L., Fodor T., Szücs M., Fülöp T., Ván P., Kovács R.: Size effects and beyond-Fourier heat conduction in room-temperature experiments, Journal of Non-equilibrium Thermodynamics 46: 4 pp. 403–411., 9 p., 2021
[S2] A. Fehér, R. Kovács.: On the evaluation of non-Fourier effects in heat pulse experiments, International Journal of Engineering Science 169 Paper: 103577, 14 p., 2021
[S3] R. Kovács, A. Fehér, S. Sobolev: On the two-temperature description of heterogeneous materials, International Journal of Heat and Mass Transfer, Volume 194, 123021, ISSN 0017-9310, 2022
[S4] Fehér Anna, Kovács Róbert: Heterogén anyagok hőimpulzus kísérletének kiértékelési eljárása, Magyar Energetika (in Hungarian) [Evaluation procedure for heat pulse experiments on heterogeneous materials] (1216-8599): 29:4 pp 2–10, 2022
[S5] Fehér Anna, Kovács Róbert: Általánosított termodinamikai modellek kísérleti kiértékelési módszertana (in Hungarian) [Experimental evaluation methodology for generalised thermodynamic models], In: Takács, Donát M.; Ván, Péter; Vásárhelyi, Balázs (Ed.) Kőzetmechanika és termodinamika, Budapest, Hungary: Egyesület a Tudomány és Technológia Egységéért, 189 p. pp. 3–16, 14 p., 2023
[S6] Anna Fehér; Róbert Kovács; Ákos Sudár; Gergely Barnaföldi: Challenges in the thermal modeling of highly porous carbon foams, Journal of Thermal Analysis and Calorimetry, (1388-6150 1572-8943): 12 p., 2024
[S7] A. Fehér, J. E. Maróti, D. M. Takács, I. N. Orbulov, R. Kovács: Thermal and Mechanical Properties of AlSi7Mg Matrix Syntactic Foams Reinforced by Al2O3 or SiC Particles in Matrix, International Journal of Heat and Mass Transfer, 2024, Accepted
[S8] A. Fehér, R. Kovács.: On the dynamic thermal conductivity and diffusivity observed in heat pulse experiments, Journal of Non-Equilibrium Thermodynamics, (0340-0204 1437-4358): Early view Paper jnet-2023-0119., 2024
[S9] Dr. Cs. Farkas et al.: Sustainable printed circuit board substrates based on flame-retarded PLA/Flax composites to reduce environmental load of electronics: quality, reliability, degradation and application tests, Sustainable Materials and Technologies 2214-9929 2214-9937: 40 pp e00902-e00917 Paper e00902., 2024
[S10] M. Gál et al.: Thermal diffusivity in copper benzene-1,3,5-tricarboxylate – reduced graphite oxide mechanical composites, Journal of Thermal Analysis and Calorimetry, Accepted, 2024
[S11] Fehér A., Markovics D., Fodor T., Kovács R.: Size effects and non-Fourier thermal behaviour in rocks, In: Li, C.C.; Odegaard, H.; Hoien, A.H.; Macias, J. (Ed.) ISRM International Symposium - EUROCK 2020, Lisboa, Portugal: International Society for Rock Mechanics and Rock Engineering, Paper: ISRM-EUROCK-2020-180, 7 p., 2020
[S12] Anna Fehér, Róbert Kovács: Observing size effects in the thermal behaviour of rocks, 18th Internal Conference of Young Scientists on Energy and Natural Sciences Issues, Conference Paper, 2022
[S13] Anna Fehér, Róbert Kovács: Analytical evaluation of non-Fourier heat pulse experiments on room temperature, 4th IFAC Workshop on Thermodynamics Foundations of Mathematical Systems Theory TFMST, 2022
[S14] Géczy, Attila; Csiszár, András; Xavier, Pascal; Corrao, Nicolas; Rauly, Dominique; Kovács, Róbert; Fehér, Anna Éva; Rozs, Egon; Gál, László: Thermal and RF Characterization of Novel PLA/Flax Based Biodegradable Printed Circuit Boards; IEEE 24th Electronics Packaging Technology Conference (EPTC), 2022
Collection of links
MTMT-profile: https://m2.mtmt.hu/api/author/10068078?&labelLang=eng
List of references.
[1] W. J. Parker, R. J. Jenkins, C. P. Butler, and G. É. Abbott. Flash method of determining thermal diffusivity, heat capacity, and thermal conductivity. Journal of Applied Physics, 32(9):1679–1684, 1961.
[2] S. Both, B. Czél, T. Fülöp, Gy. Gróf, Á. Gyenis, R. Kovács, P. Ván and J. Verhás. Deviation from the Fourier law in room-temperature heat pulse experiments. Journal of Non-Equilibrium Thermodynamics, 41(1):41–48, 2016.
[3] P. Ván, A. Berezovsky, T. Fülöp, Gy. Gróf, R. Kovács, Á. Lovas and J. Verhás. Guyer-Krumhansl-type heat conduction at room temperature. EPL, I118(5):50005, 2017. arXiv: 1704.00341v1.
