Pattantyús-Ábrahám Géza Gépészeti Tudományok Doktori Iskola 

BME Gépészmérnöki Kar, Energetikai Gépek és Rendszerek Tanszék

Témavezető: Dr. Kovács Róbert Sándor

Nem-Fourier hővezetés a mindennapokban

A kutatási téma néhány soros bemutatása

A hőimpulzus-kísérlet egy jól ismert és elterjedt módszer a különféle anyagok hőfokvezetési tényezőjének meghatározására. Az elmúlt években megfigyelték, hogy a heterogén anyagok termikus viselkedése eltérést mutat a klasszikus Fourier-egyenlettől, eltérő hőfokvezetési tényezőt eredményez, és ennek megbízható meghatározásához szükség van további termikus paraméterek ismeretére.

 

A kutatóhely rövid bemutatása

 

Az Energetikai Gépek és Rendszerek Tanszéken már több évtizedes hagyománya van a hővezetéssel kapcsolatos kutatásoknak, amelyben kiemelkedő szerepe volt Kiss László, Gróf Gyula és Környey Tamás munkásságának. A tanszéken jelenleg az Irreverzibilis Termodinamika Kutatócsoport foglalkozik hővezetési kutatásokkal, én ennek a csoportnak a tevékenységében veszek részt.

 

A kutatás történetének, tágabb kontextusának bemutatása

 

A mérnöki tudományok különféle területein (mint például hőtan, szilárdközeg- és folyadékmechanika, diffúziós jelenségek) meglehetősen sokféle anyagi viselkedést leíró modellt használnak, az adott fizikai feladatnak megfelelően. Az utóbbi években az anyagi viselkedés modellezésében a termodinamika kiemelkedő jelentőséggel kezdett bírni, lehetővé téve a meglévő modellek érvényességi tartományának egy fizikailag erős módszertan segítségével történő konzisztens kiterjesztését.

 

A korszerű gyártástechnológiáknak köszönhetően a mérnöki alkalmazásokban olyan anyagok/anyagszerkezetek jelentek meg, amelyek leírása a klasszikus és jól ismert Fourier-törvénnyel már nem feltétlenül végezhető el a kívánt pontossággal.

 

A kutatás során Orbulov Imre kutatócsoportjától kapott fémhabokat vizsgálunk hőtároló szerkezet fejlesztése céljából. Vizsgálunk még szénhabokat, a CERN-ALICE újgenerációs detektor mechanikai és hővezetési rendszereinek részeiként. Ezen felül gáztárolásra használatos fémorganikus térhálós minták is rendelkezésre állnak, melyeket László Krisztina kutatócsoportjával való együttműködés keretében kutatunk.

 

A kutatás alapvető motivációja, hogy választ adjunk arra, hogyan lehet termikusan jellemezni az összetett struktúrájú anyagokat. Ilyen jellemzésre a hőimpulzus-kísérlet egy bevett, standard módszertan. A Fourier-egyenlettel való kiértékelés már régóta ismert a hőimpulzus-kísérlethez, azonban a heterogén anyagok esetében a kísérletből kapott mérési adatokat nem írja le kellő pontossággal, ezért a cél ennek fejlesztése és kiterjesztése. A kutatásunktól függetlenül a NETZSCH is mért hasonló jelenségeket, így a kutatás folytatása még jelentőségteljesebbé válik.

 

A kutatás célja, a megválaszolandó kérdések

 

A kutatás célja és a hangsúly az általánosított hővezetési modellek alkalmazhatóságának, gyakorlatba való átültetésének a vizsgálatán van. Ehhez egyfelől az irodalomból elérhető kísérletek elemzése, másfelől pedig saját kísérletek végzése vezet, amely által megérthetővé és ezáltal tervezhetővé válnak az eddig csupán felületesen ismert fizikai jelenségek, mint például a heterogenitások hővezetésre gyakorolt hatása.

Modellezés szempontjából kétféle típust különböztetünk meg. Az első, amikor az adott anyagot, szerkezeti tulajdonságait pontosan ismerjük és kihasználjuk, azonban ez nem egy általánosan használható módszertant eredményez. A másik, általam használt lehetőség az effektív modellezés, ez nem épít a pontos anyagi struktúra ismeretére, így működik a Fourier-törvény is, ezáltal szélesebb körben és hatékonyabban használható a modell.

A fókusz a kutatásom során a kísérleteken és azok kiértékelésén van. A kiértékelések során a Fourier-egyenleten túl több alternatív hővezetési modellt is tesztelek, illetve azok gyakorlatba való átültethetőségét. A cél a Fourier-egyenlet alkalmazhatósági tartományának megfogalmazása, korlátjainak felismerése.

A kutatás során az előbb említett, a gyakorlat számára fontos anyagokat tervezem vizsgálni. Szükség van még a kísérletek kiértékelési módszertanának fejlesztésére a Fourier-től eltérő modellek miatt. Ezen felül tervezem egy másik jellegű kísérlet felépítését, amelyben a hőimpulzusok száma és azok hossza programozható, ezáltal mélyítve az eddigi megértésünk a jelenségről. Ehhez az eszközök rendelkezésemre állnak.

 

Módszerek

 

A hőimpulzus mérési metódus [1] (1. ábra) segítségével a behelyezett minta hőfokvezetési tényezőjét van lehetőségünk meghatározni szobahőmérsékleten. A behelyezett minta előlapját egy hőimpulzussal gerjesztjük, amit esetünkben egy villanó lámpa ad, melynek impulzushossza rövid, 0.01 másodperc. Az impulzus hatását a minta hátoldalán egy termoelemmel mérjük, mely villamos jelet szolgáltat és egy PC oszcilloszkóppal digitalizáljuk az adatokat. Mivel a kísérleti berendezés zárt, ezért a villanás megtörténtét egy fotovoltaikus érzékelő jelzi, mely a mintatartó mellett helyezkedik el. A mintadarabokat a kísérlet elvégzése előtt elő kell készíteni minden esetben (abszorbció, kontaktok biztosítása). A kísérleti adatok feldolgozásában egy konzisztens, egységes Fourier, és nem-Fourier modelleket is felhasználó kiértékelési módszertanra van szükség [2].

 

 

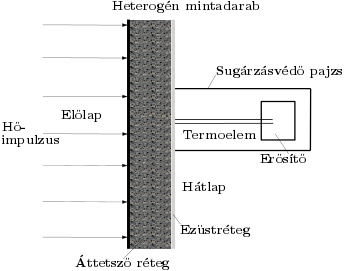
1. ábra: a hőimpulzus kísérlet elrendezése

 

A modellezés során többféle hővezetési modellt vizsgálok. Az első minden esetben a Fourier-egyenlet, azonban emellett három alternatív modellel foglalkozom. Ezen modellek a kéthőmérséklet-modell, a Guyer-Krumhansl-egyenlet [3], valamint a Jeffreys-egyenlet. A korábbi vizsgálatok során azt tapasztaltam, hogy a kéthőmérséklet-modell túl sok illesztendő paramétert tartalmaz, az illesztések paraméterei nem egyértelműek, így ennek alkalmazását és további vizsgálatát kizártam. A kiértékelésekre egy érzékenységi függvényeken alapuló iteratív eljárást dolgoztam ki. A mintákon a Guyer-Krumhansl-egyenletet sikerrel alkalmaztam, a kiértékelési eljárás finomítása és további tesztelése még hátra van. A Jeffreys-egyenlet alkalmazhatóságának vizsgálata pedig folyamatban van, vele együtt ennek tesztelése, valamint kiértékelési metódusának kidolgozása is.

 

A további vizsgálatok és hőimpulzus kísérletek elvégzéséhez egy másik lámpa is rendelkezésre áll, amely nem egyszeri villanásra képes, hanem programozható módon több hőimpulzus is adható a behelyezett mintára. Ezzel tesztelhető, hogy a modellek és a kiértékelési módszertanok mennyire és milyen módon érzékenyek több és másféle peremfeltétel meglétére. Az eszközháttér a kísérletek elvégzéséhez már rendelkezésre áll, mellyel a már eddigi kísérleteket tervezem újból elvégezi más-más beállításokkal, melyet az új lámpa és eszköz megenged.

 

Eddigi eredmények

Az eddigi kutatások során a többféle típusú és szerkezetű anyagok vizsgálata során azt állapítottam meg, hogy a Fourier-egyenlet által adott hőfokvezetési tényező egy nem-Fourier adatsoron nem határozható meg megbízhatóan. Az alternatív modellek vizsgálatával a Guyer-Krumhansl-egyenlethez sikerült felépíteni egy megfelelő és konzisztens kiértékelési metódust, ami további alternatív modellre is átültethető. Kidolgoztam egy érzékenységi függvények vizsgálatán alapuló iteratív eljárást, melyet a modell ismeretlen paramétereinek meghatározására használok fel. Ezen kiértékelések elvégzésével jellemeztem hétféle kőzettípust, kétféle szénhabot, ötféle kompozit fémhabot és kétféle fémorganikus térhálós anyagot.

 

A Guyer-Krumhansl-egyenletet használva összefüggést lehet látni a Fourier-egyenlettel. A Guyer-Krumhansl-egyenlet időskáláinak átlaga megadja a Fourier-egyenlet által adott hőfokvezetési tényezőt, így összeköthető egy egyszerű összefüggéssel a két modell. Ezek alapján az alternatív modellből vissza lehet származtatni a Fourier-egyenletben használható hőfokvezetési tényezőt. Így azt lehet mondani, hogy a Fourier-egyenlet alkalmazható a nem-Fourier anyagokra is, azonban csak korlátozott módon. Ilyen összefüggés a többi alternatív modell szempontjából még ismeretlen. Jelentős eredménynek mondható, hogy a Guyer-Krumhansl-egyenlet egyformán használható volt a különféle anyagokra, így ez egy általános modellt, illetve megközelítést ad az anyagok jellemzésére.

 

 

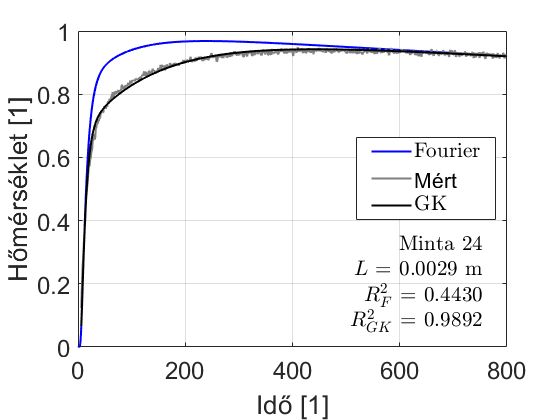
2. ábra: Fémhab minta kiértékelése a Fourier-egyenlettel és a Guyer-Krumhansl-egyenlettel.

 

Általános modell esetén olyan modellt értünk, ami esetében maguk a modellben szereplő paraméterek függenek az anyagi struktúrától, azonban a struktúra pontos ismeretére nincs szükség, hanem ezek effektív módon vehetők figyelembe a modellezés szempontjából. Ebből adódóan a heterogén anyagok termikus modellezéséhez nincs szükség a szerkezet pontos modellezésére és ezáltal szuperszámítógépek használatára, és rendkívül energiaigényes számítási kapacitásra. Hosszútávú cél a kiterjesztett hővezetési egyenlet extra paraméterei és a heterogén struktúra közötti kapcsolat feltérképezése és tervezhetővé tétele.

 

Várható impakt, további kutatás

 

A kutatás folytatásaképpen további kísérleteket fogok elvégezni és a különféle alternatív modellek tesztelése, valamint gyakorlatba való átültetése is folyamatban van. A kutatás és a kidolgozott módszertan választ tud adni arra a kérdésre, hogy hogyan lehet az összetett, bonyolult anyagi struktúrával rendelkező szerkezeteket modellezni, valamint hogyan lehet egy végeselemes környezetbe beépíteni ezeket a termikus paraméterek meghatározásával, ami várhatóan a mérnöki gyakorlat minden területére nagy hatással lesz. A meglevő mintáknak közvetlen gyakorlati hasznosulását látjuk az energetika több területén (gáztárolás, hőtárolás, hatékonyságnövelés), valamint precízebb méréstechnikai eszközök (CERN) fejlesztésében egyaránt.

 

 

 

Saját publikációk, hivatkozások, linkgyűjtemény

Kapcsolódó saját publikációk listája.

 

Fehér A., Lukács N., Somlai L., Fodor T., Szücs M., Fülöp T., Ván P., Kovács R.: Size effects and beyond-fourier heat conduction in room-temperature experiments, JOURNAL OF NON-EQUILIBRIUM THERMODYNAMICS 46: 4 pp. 403–411, 9 p. (2021)

 

A. Fehér, R. Kovács.: On the evaluation of non-Fourier effects in heat pulse experiments, INTERNATIONAL JOURNAL OF ENGINEERING SCIENCE 169 Paper: 103577, 14 p. (2021)

 

R. Kovács, A. Fehér, S. Sobolev: On the two-temperature description of heterogeneous materials, International Journal of Heat and Mass Transfer, Volume 194, 2022, 123021, ISSN 0017-9310

 

Fehér Anna, Kovács Róbert: Heterogén anyagok hőimpulzus kísérletének kiértékelési eljárása, MAGYAR ENERGETIKA (1216-8599): 29:4 pp 2–10 (2022)

 

Anna Fehér; Róbert Kovács; Ákos Sudár; Gergely Barnaföldi: CHALLENGES IN THE THERMAL MODELING OF HIGHLY POROUS CARBON FOAMS, Journal of Thermal Analysis and Calorimetry, 2023, bírálat alatt

 

Fehér Anna, Kovács Róbert: Általánosított termodinamikai modellek kísérleti kiértékelési módszertana, In: Takács, Donát M.; Ván, Péter; Vásárhelyi, Balázs (szerk.) Kőzetmechanika és termodinamika, Budapest, Magyarország: Egyesület a Tudomány és Technológia Egységéért (2023) 189 p. pp. 3–16. , 14 p.

 

Fehér A., Markovics D., Fodor T., Kovács R.: Size effects and non-Fourier thermal behaviour in rocks, In: Li, C.C.; Odegaard, H.; Hoien, A.H.; Macias, J. (szerk.) ISRM International Symposium - EUROCK 2020, Lisboa, Portugália: International Society for Rock Mechanics and Rock Engineering (2020) Paper: ISRM-EUROCK-2020-180 , 7 p.

 

Anna Fehér, Róbert Kovács: Observing size effects in the thermal behaviour of rocks, 18TH INTERNATIONAL CONFERENCE OF YOUNG SCIENTISTS ON ENERGY AND NATURAL SCIENCES ISSUES, 2022

 

Anna Fehér, Róbert Kovács: Analytical evaluation of non-Fourier heat pulse experiments on room temperature, 4th IFAC Workshop on Thermodynamics Foundations of Mathematical Systems Theory TFMST 2022

 

Géczy, Attila; Csiszár, András; Xavier, Pascal; Corrao, Nicolas; Rauly, Dominique; Kovács, Róbert; Fehér, Anna Éva; Rozs, Egon; Gál, László: Thermal and RF Characterization of Novel PLA/Flax Based Biodegradable Printed Circuit Boards; 2022 IEEE 24th Electronics Packaging Technology Conference (EPTC)

 

 

Hivatkozások listája.

 

[1]    W. J. Parker, R. J. Jenkins, C. P. Butler és G. É. Abbott. Flash method of determining thermal diffusivity, heat capacity, and thermal conductivity. Journal of Applied Physics, 32(9):1679–1684, 1961.

 

[2]    S. Both, B. Czél, T. Fülöp, Gy. Gróf, Á. Gyenis, R. Kovács, P. Ván és J. Verhás. Deviation from the Fourier law in room-temperature heat pulse experiments. Journal of Non-Equilibrium Thermodynamics, 41(1):41–48, 2016.

 

[3]    P. Ván, A. Berezovsky, T. Fülöp, Gy. Gróf, R. Kovács, Á. Lovas és J. Verhás. Guyer-Krumhansl-type heat conduction at room temperature. EPL, I118(5):50005, 2017. arXiv: 1704.00341v1.