|
|
BMe Kutatói pályázat |
|
Pattantyús-Ábrahám Géza Gépészeti Tudományok Doktori Iskola
BME Gépészmérnöki Kar, Műszaki Mechanikai Tanszék
Témavezető: Dr. Dombóvári Zoltán
Ipari robotok által megvalósított megmunkálási folyamatok modellezése
A kutatási téma néhány soros bemutatása
Manapság egyre növekvő ipari igény van arra, hogy ipari robotokat fém munkadarabok megmunkálására használják. Ez – főképp simító megmunkálások esetén – a szerszámgépek költséghatékony, illetve sokoldalú alternatívája lehet. A robotok a következő két hátránnyal rendelkeznek ezen a téren. Dinamikai tulajdonságaik messze alul maradnak a szerszámgépekének, illetve szerkezetük hajlamos erős nemlineáris viselkedést mutatni [H1]. Továbbá a marási eljárások regeneratív folyamatok [H2], mivel a dinamikai rendszer múltbeli állapotváltozói fontos szerepet játszanak a rendszer hosszú távú viselkedésében. Ez a regeneratív hatás nagy amplitúdójú, úgynevezett „chatter” rezgéseket okozhat, amelyek szinte mindig behatárolják a megmunkálási folyamat paramétereit. Ha ezekre a problémákra iparban is elfogadható megoldás születik, akkor a robotok jelentős szerepet kaphatnak a jövőben fémek megmunkálása terén.
A kutatóhely rövid bemutatása
Kutatómunkámat a BME GPK Műszaki Mechanikai Tanszékén végzem. Emellett részt veszek az MTA-BME Lendület Szerszámgéprezgések Kutatócsoport munkájában is. A kísérleti vizsgálatok egy részét a Spanyolországban található IDEKO kutató központtal közösen végzem. További kutatási együttműködésben állok a Bristoli egyetemmel (University of Bristol), a Georgiai technológiai intézettel (Georgia Institute of Technology) és a Baszk Alkalmazott Matematika Központtal (Basque Center for Applied Mathematics).
A kutatás történetének, tágabb kontextusának bemutatása
A legelső robotokat leginkább tárgyak mozgatására fejlesztették ki [H3], ahol a kimagasló geometriai pontosság nem volt szükséges. Később már használták ezeket egyes megmunkálási folyamatok esetén is, különösen agyagból készült prototípusok előállítására. Ekkorra a pozícionálás pontossága már egy nagyságrendet fejlődött, amit jobb szenzorok és beépített proporcionális-derivatív visszacsatolású szabályozás segítségével értek el. Ez az elérhető pontosság elegendő volt a korábban említett agyag szoborfelületek esetén, ahol a megmunkálásból származó erők nem különösebben nagyok. A 3D polimer nyomtatási technológiák megjelenésével ugyan a robotokkal való prototípusgyártási formák háttérbe szorultak, de egyes esetekben még manapság is használatosak agyag prototípusok, például autó karosszéria fejlesztésnél, alacsony költségük és tartósságuk miatt.
A fém munkadarabok ipari robotokkal való megmunkálásának lehetősége ígéretesnek tűnik a szerszámgépekhez viszonyított sokoldalúságuk és relatíve alacsony költségük miatt. A legtöbb nyílt kinematikai láncú robot kitűnően használható szoborfelületek megmunkálására, emellett nagy munkatérrel is rendelkeznek. Ennek a sokoldalú konfigurációnak fém alkatrészek esetén komoly hátránya az alacsony dinamikus merevség. Ezen felül a robotok hajtóművei hajlamosak erős nemlineáris tulajdonságokat mutatni, ami bizonyos esetekben kedvezőtlenül hathat a rendszer robusztusságára. Végül a robotok rezgési paraméterei függenek a karok pozíciójától, ezáltal nagymértékben változhatnak a megmunkálás során. Ez mind a kísérleti dinamikai jellemzést, mind a szimulációkat nehézkessé teszi.
A kutatás célja, a megválaszolandó kérdések
A kutatás célja, hogy a fém alkatrészek ipari robotokkal való megmunkálásának akadályaira iparban is felhasználható megoldásokat nyújtsunk. A robotok helyes kísérleti jellemzése ugyanannyira fontos szerepet játszik, mint a helyes matematikai eszköztár megalkotása. A megoldandó nehézségek mind kísérleti, mind elméleti téren jelen vannak.
A kutatás során használt módszerek alkalmasak arra, hogy folyamattervezési irányelveket jelöljenek ki, illetve dinamikai megoldásokat nyújtsanak a megfelelő stabilitás és robusztusság biztosításával. A legfőbb problémák közé tartoznak: a csuklókból és hajtóművekből származó rendszerint erős nemlineáris merevségi karakterisztika, a megmunkálásból (regeneratív hatás) és késleltetett szabályozásokból származó instabilitási problémák, illetve a végeffektor pozíciójától függő időben változó dinamikai tulajdonságok. Egy egyesített tervezési és fejlesztési megközelítés biztosítása érdekében a nehézségek különböző aspektusait érdemes először külön-külön tanulmányozni. A fent említett jelenségek számos eltérő mérnöki problémában előfordulnak, így a kutatás során megalkotott általánosan megfogalmazott matematikai megközelítés értékes lehet más tanulmányok esetén is.
Módszerek
Gyorsulás-visszacsatolású szabályozás használata a dinamikai tulajdonságok javítására
A megfelelő minőség eléréséhez a robotok dinamikai tulajdonságait javítani kell fém munkadarabok megmunkálása esetén. Habár ez viszonylag könnyedén megvalósítható lenne egy online szabályozási körrel a beépített szabályozó sebesség- vagy gyorsulásjeleit felhasználva, a gyártó biztonsági okokból általában nem ad hozzáférést a beépített szabályozókhoz. Ez a relatíve egyszerű, további berendezéseket nem igénylő megoldás tehát ipari megoldásként nem jöhet szóba. Másik megközelítés passzív vagy szemi-aktív rendszerek használatával a végeffektor dinamikus merevségének növelése. A tapasztalat azonban az, hogy az ipari felhasználók ódzkodnak ezektől a szerkezetet megváltoztató módszerektől.
Egy további gyorsulás-visszacsatolású szabályozás használata a már beépített pozicionáló proporcionális-derivatív szabályozó mellett alacsony költségű és egyszerű megoldás lehet a stabilitás és robusztusság javítására. Ebben az esetben a stabil megmunkálás megvalósítás feltétele az új szabályozó paramétereinek gondos megválasztása és az időkésés helyes szinkronizálása a beépített szabályozási kör időkésésével. Elméletileg a meghajtásból származó nemlineáris viselkedéséből származó kedvezőtlen hatások is ellensúlyozhatók nemlineáris karakterisztikájú szabályozó segítségével [F1].
Digitális kontrollerek kvantálásának hatása
A modern digitális kontrollerekben jelenlévő kvantálásnak jelentős hatása lehet a mechanikai rendszer stabilitására, ami a különböző jel periódusok együttes hatásából származik. Ez kifejezetten igaz neutrális és siettetett differenciálegyenletek esetén [H4], ahol az állapotváltozók deriváltja függ múltbéli állapotváltozók deriváltjától vagy második deriváltjától. Az időkésések ezekben a digitális rendszerekben fűrészfogszerű jelekként modellezhetők, amelyek periodikus időkésés függvényeket adnak. Az időkésések periodikussága és a lehetséges megmunkálási folyamatok lehetséges periodikussága határozza meg az úgynevezett főperiódust, amely fontos szerepet játszik a stabilitás számításokban.
Robotok időben változó dinamikai paramétereinek hatása
Ipari robotok rezgési paraméterei általában erősen függenek a robot pozíciójától. A megmunkálás során ezek a paraméterek széles skálán változhatnak az előírt pályától függően. Az ilyen rendszerek matematikai leírása nemautonóm (általánosan nem periodikus) időben folytonosan változó paraméterű dinamikai rendszerekhez vezet. Ilyen esetben a matematikailag viszonylag egyszerűen megfogalmazható aszimptotikus stabilitás biztosítása a folyamat teljes időintervallumán általában nem lehetséges. Elérhető célként megfogalmazható mérnökileg gondosan megválasztott rezgési amplitúdóhatárok betartása, amit az irodalomban véges idejű stabilitásnak neveznek. Ez megfelelő és teljesíthető követelményt biztosíthat az előírt minőség eléréséhez. Habár ezen kritériumok tervezése egyszerű, teljesülésének matematikai meghatározása nehézkes, mivel a rezgési amplitúdók pontos becslése szükséges.
A nemautonóm dinamikai modell vizsgálata közel sem triviális és az elérhető numerikus módszerek még a legegyszerűbb esetekben sem adnak megbízható eredményeket. Emiatt szükséges egy olyan analitikus közelítő módszer megalkotása, amivel a véges idejű stabilitás megbízhatóan számítható, illetve megfelelő alapot nyújt későbbi alkalmas numerikus sémák megalkotásához.
Eddigi eredmények
Hopf-bifurkáció-számítás neutrális késleltetett differenciálegyenletekre
A korábban említett ipari robotok legegyszerűbb ekvivalens modelljeként egy két szabadságfokú nemlineáris robot modell szolgált. Ehhez csatlakozik a nemlineáris késleltetett gyorsulás-visszacsatolású szabályozó, amelynek feladata a stabilitás és robusztusság biztosítása. A leírt rendszer mozgásegyenlete matematikailag neutrális késleltetett differenciálegyenletként modellezhető.
A rendszer lineárisstabilitás-vizsgálatának eredménye az 1.(b) ábrán látható. A kritikus bifurkációs pont közelében jellemző nemlineáris viselkedést a centrálissokaság-redukcióval írható le, amelynek egyenletei új eredmények neutrális egyenletek esetében [F2]. A közelítő analitikus számítás eredményeit érdemes numerikus követő módszer [H5] segítségével ellenőrizni. Ennek az eredményeit mutatja be 1. (c,d) ábra. Elmondható, hogy a megfelelő nemlineáris szabályozó paraméterek megválasztásával a kezdetben instabil határciklusok stabil periodikus pályákká formálhatók, amivel a rendszer perturbációra való érzékenysége csökken.
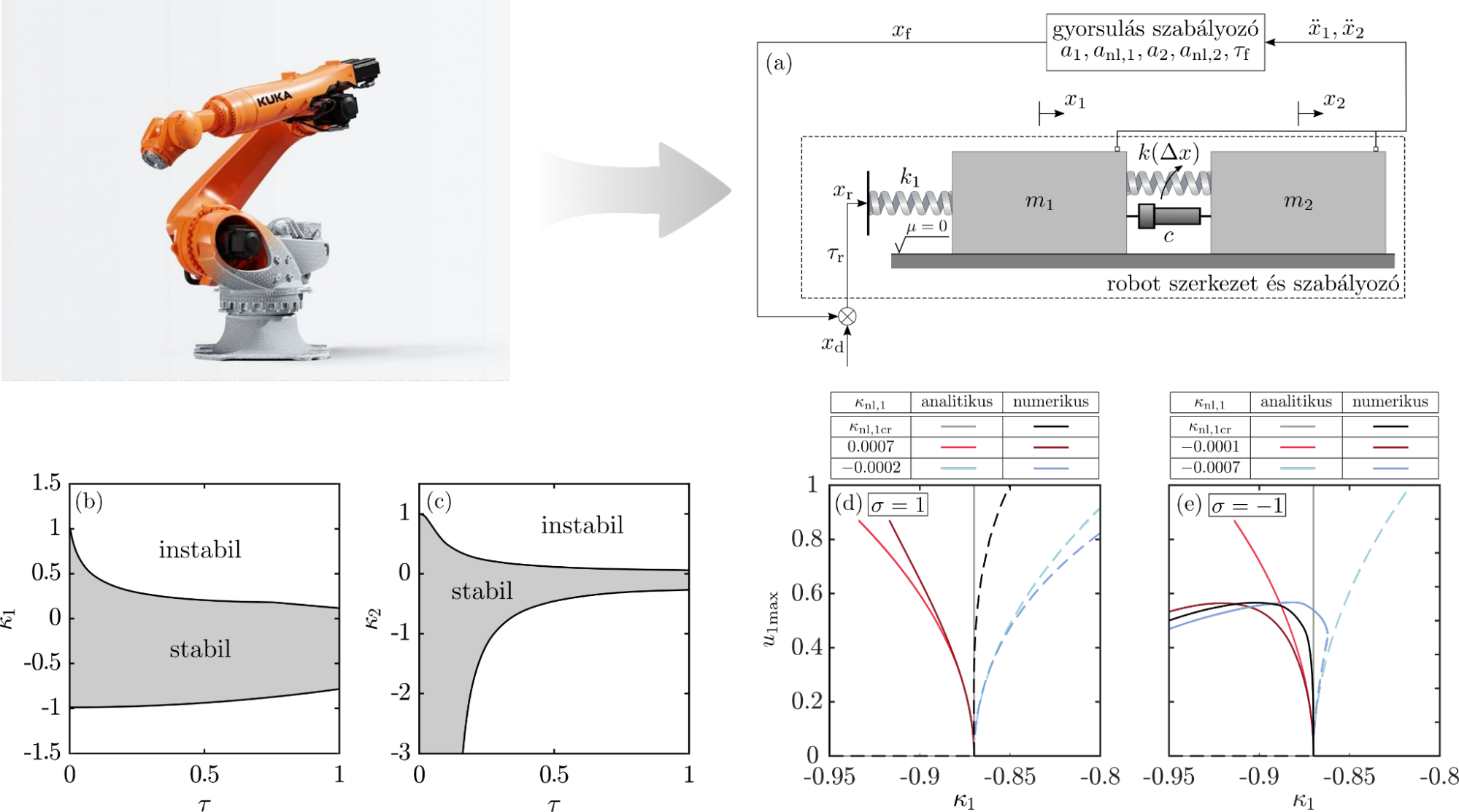
1. ábra: (i) két szabadságfokú robot modell. (a,b) lineáris stabilitás vizsgálat. analitikus és numerikus eredmények bifurkációs eredmények felkeményedő (c) és kilágyuló (d) merevségre.
Robotmegmunkálás stabilitása digitális szabályozókkal
A digitális hatások modellezésére a szemidiszkretizáció módszerét [H6] általánosítottam egy programcsomagban. A főperiódus közelítésére alkalmas módszert biztosít a Farey- hányados használata. A numerikus módszert két mérnöki alkalmazási példán szemléltettem.
Elsőként egy önvezető autó hierarchikus szabályozása stabilitásvizsgálatának meghatározása volt a cél. Az elméleti eredmények kiváló megfelelést mutatnak a kisskálájú futópados méréssekkel [F3]. Másik példaként egy robotkarral való marási megmunkálási folyamat stabilitásának meghatározása szolgált. Az eredeti digitális proporcionális-derivatív szabályozó mellé beépített digitális gyorsulásszabályozó hatását szemlélteti a 3.ábra. A stabilitási térképeken jól látható, hogy a szabályozási paraméter és a visszacsatolás késésének helyes megválasztásával a kritikus forgácsvastagság drasztikusan növelhető [K2, F4].
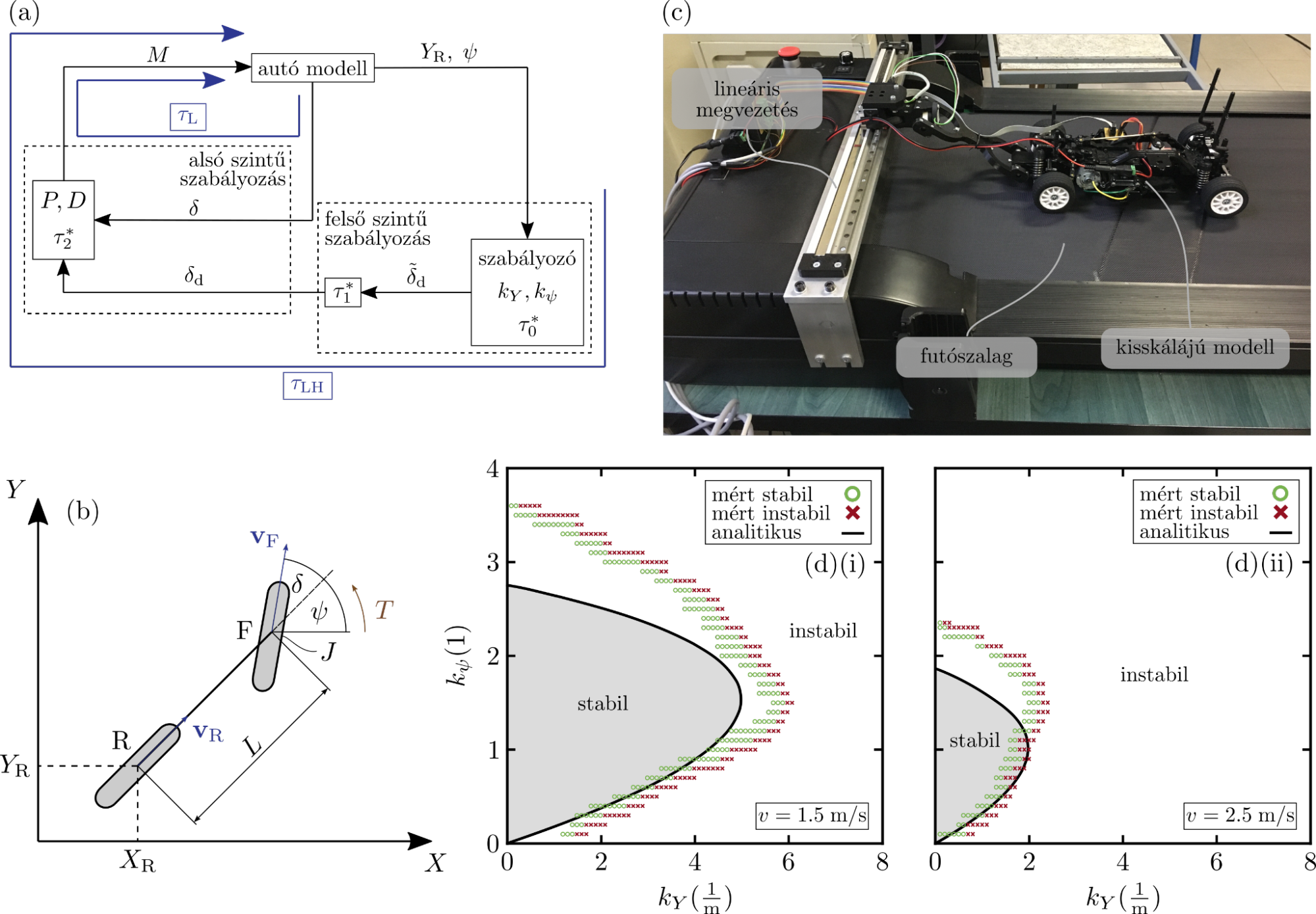
2. ábra: (a) hierarchikus kormányszabályozás. (b) biciklimodell merev kerék-talaj kapcsolattal. (c) mérési összeállítás. (d) elméleti és kísérleti stabilitástérképek különböző jármű sebességek esetén.
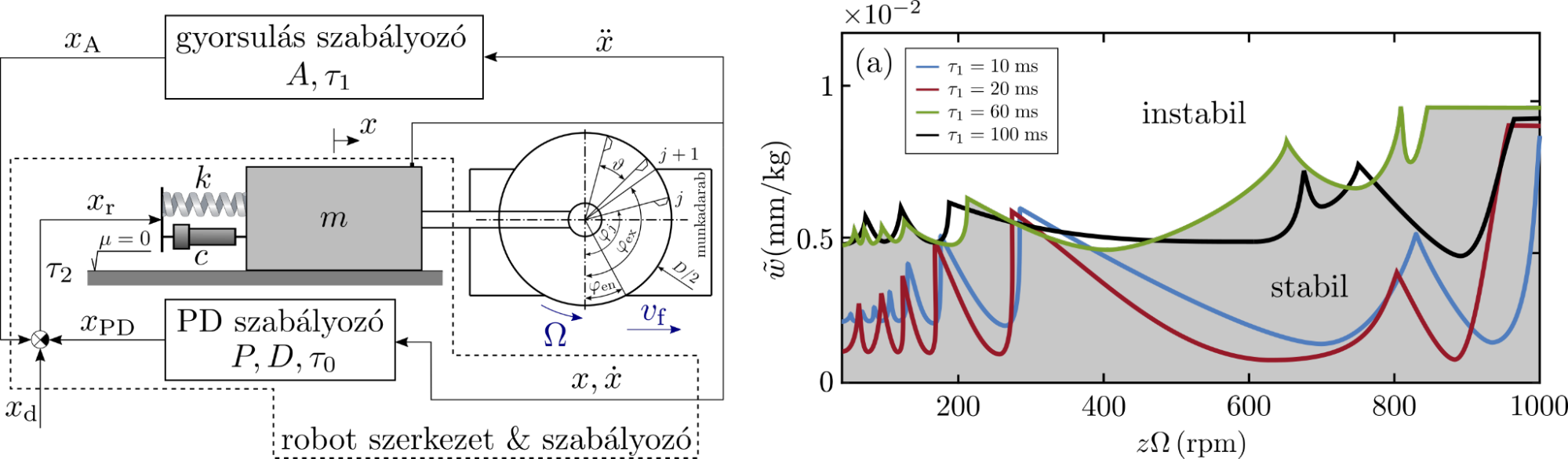
3. ábra: (a) robotszerkezet marás közben, digitális gyorsulás visszacsatolású szabályozással. (b) stabilitás különböző mintavételezési időkésésekre.
Időben változó paraméterű rendszerek véges idejű stabilitásának analitikus közelítése
A korábban említett nemautonóm dinamikai rendszerek véges idejű stabilitási tulajdonságainak megfelelő számításához egy analitikus keretrendszer megalkotása szükséges. A homogén megoldás közelíthető a jól ismert WKB módszer [H7] segítségével. A partikuláris megoldásra megfelelő közelítést ad az új iteratív parciális integráláson alapuló módszer (IIBP) [K1, F5]. A módszer szemléltetéséhez jó példa a mérnökileg is releváns két szabadságfokú modell időben változó paraméterekkel. Az 1.(ii)(a, b) ábra a klasszikus numerikus sémák véges idejű stabilitásának pontatlanságát szemlélteti nagy időintervallumok esetén, míg az 1.(ii)(c, d) ábra az analitikus megoldás kiváló pontosságát mutatja kis időintervallumokra.
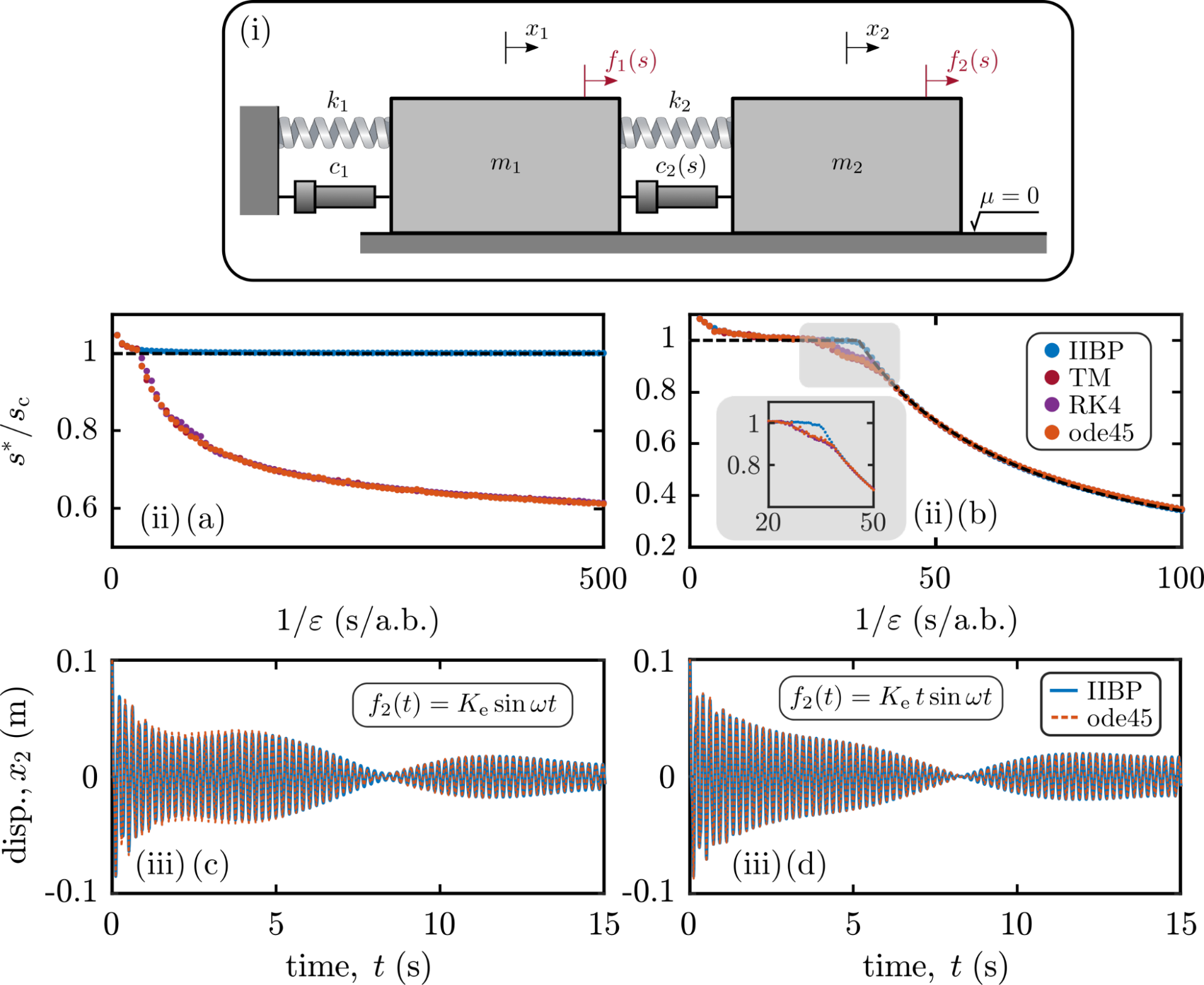
4. ábra: (a) időben változó paraméterű két szabadságfokú modell. (ii) IIBP módszer összehasonlítása klasszikus numerikus sémákkal (ii) időbeli szimulációk.
Várható impakt, további kutatás
Ha megoldás születik a robotokkal való megmunkálások jelen problémáira, akkor számos feladatot átvehetnek a szerszámgépektől, csökkentve ezzel gépidőt és előállítási költséget. Ez az újszerű megoldás nagy hatással lehet a jövőbeli megmunkálási folyamatok tervezésére.
A kutatás eredményei nem csak a robotokkal megvalósított megmunkálás területén fontosak, de általánosan használható módszereket kínálnak számos más mérnöki probléma megoldásához. A jövőbeli kutatás legfontosabb eleme az elméleti ötletek és eredmények kísérleti megvalósítása. Ez egy fontos lépés az ipar számára alkalmas megoldások kifejlesztésében.
Saját publikációk, hivatkozások, linkgyűjtemény.
Kapcsolódó saját publikációk listája.
Folyóiratcikkek.
[F1] Habib G., Bártfai A., Barrios A., Dombóvári Z. Bistability and delayed acceleration feedback control analytical study of collocated and non-collocated cases. Nonlinear Dynamics, 108, 2075–2096, 2022. (IF: 5.741)
[F2] Bartfai A., Dombovari Z., Hopf Bifurcation Calculation in Neutral Delay Differential Equations: Nonlinear Robotic Arms Subject to Delayed Acceleration Feedback Control. International Journal of Non-Linear Mechanics, 147, 2022. (IF: 2.985)
[F3] Bartfai A., Vörös I., Takacs D., Stability analysis of a digital hierarchical steering controller of autonomous vehicles with multiple time delays. Journal of Vibration and Control, OnlineFirst, 2023 (IF: 2.633)
[F4] Bartfai A., Barrios A., Dombovari Z., Stability Analysis of a One Degree-of-Freedom Robot Model with Sampled Digital Acceleration Feedback Controller in Turning and milling. Journal of Computational and Nonlinear Dynamics, 18(8), 2023. (IF: 1.872)
[F5] Bartfai A., Ponce-Vanegas F., Kuske R., Hogan J., Dombovari Z., Framework for the analytical approximation of finite time stability of excited dynamical systems with time-varying parameters. SIAM Journal on Applied Mathematics, 2023. (elbírálás alatt, IF: 2.148)
[F6] Ponce-Vanegas F., Bartfai A., Dombovari Z., Semi-analytical solutions for slowly varying linear equations. (beküldés folyamatban)
Konferenciacikkek / Könyvfejezetek
[K1] Bartfai A., Kuske, R., Dombovari, Z., On the finite-time stability of dynamic stability loss in a single degree of freedom system. In Proceedings of the ISMA2022 International Conference on Noise and Vibration Engineering, Leuven, 2565–2576, 2022.
[K2] Bartfai A., Barrios, A., Dombovari, Z., Stability Analysis of a One Degree-of-Freedom Robot Model with Sampled Digital Acceleration Feedback Controller in Turning. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference (ASME IDETC-CIE2022), St. Louis, 1–8, 2022.
[K3] Bartfai A., Dombovari Z., Demonstration of optimal tuning measurement of the tuneable clamping table with a polymer workpiece. 38th Danubia Adria Symposium on Advances in Experimental Mechanics, 2022, no. 3125.
[K4] Bartfai A., Dombovari Z., Bistability in nonlinear elastic robotic arms subject to delayed feedback control. 10th European Nonlinear Dynamics Conference (ENOC 2022), Lyon, 1113–1114, 2022.
[K5] Bartfai A., Barrios A., Dombovari Z., Robotic Machining Applications: Delayed Acceleration Feedback Control in Milling. Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference (ASME IDETC-CIE2021), online, 2021, no. 73909.
[K6] Bártfai A., Dombóvári Z., A Case Study on the Stabilization of Advanced Delay Differential Equations with Digital Controllers. 15th IFAC Workshop on Time Delay Systems (TDS2021), online, pp. 234–235, 2021.
[K7] Bártfai A., Vörös I., Takács D., Időkésés és mintavételezés hatása egy autó sávtartó szabályozásában. XXIX. Nemzetközi Gépészeti Konferencia, Kolozsvár (OGÉT 2021), 204–207, 2021.
[K8] Iklodi Zs., Gabos Z., Bartfai A., Dombovari Z., Time Domain simulation of surface topography in broaching considering tools with general cutting-edge geometries and three DoF parametric dynamics. Manufacturing Engineering Society International Conference (MESIC 2023), Sevilla, pp. 3–12, 2023
[K9] Bartfai A., Dombovari Z., Demonstration of finite time stability in hardware-in-the-loop turning process with time-varying parameters. 39th Danubia Adria Symposium on Advances in Experimental Mechanics (DAS 39th), Siófok, pp. 72–73, 2023
[K10] Bartfai A., Dombovari Z., Időben változó paraméterű esztergálás véges idejű stabilitás vizsgálatának numerikus szimuláció problémája. XIV. Magyar Mechanikai Konferencia, Miskolc (MAMEK XIV.), 2023
Linkgyűjtemény
MTA-BME Lendület Szerszámgéprezgések Kutatócsoport
Hivatkozások listája
[H1] de Luca A., Farina R., Lucibello P., On the control of robots with visco-elastic joints. In: Proceedings. 2005 IEEE International Conference on Robotics and Automation, 4297–4302, 2005
[H2] Munoa J., Beudaert X., Dombovari Z., Altintas Y., Budak E., Brecher C., Stepan G., Chatter suppression techniques in metal cutting. CIRP Annals 65(2), 785–808, 2016.
[H3] Hazarika S.M., Dixit U.S., Robotics: history, trends, and future directions, chap. 7. Materials Forming, Machining, and Tribology. Springer International Publishing, 213–239, 2018.
[H4] Insperger T., Stepan G., and Turi J., Delayed feedback of sampled higher derivatives. Philosophical Transactions of the Royal Society A 368(1911): 469–482, 2010.
[H5] Barton D.A. Krauskopf B., Wilson R.E., Collocation schemes for periodic solutions of neutral delay differential equations. Journal of Difference Equations and Applications, 12(11), 1087–1101, 2006.
[H6] Insperger T., Semi-Discretization for Time-Delay Systems. Springer-Verlag New York: Stability and Engineering Applications, 2011.
[H7] Baer S.M., Erneux T., Rinzel J., The slow passage through a Hopf bifurcation: Delay, memory effects, and resonance. SIAM Journal on Applied Mathematics, 49(1), 55–71, 1989.
