Pattantyús-Ábrahám Géza Gépészeti Tudományok Doktori Iskola 

BME Gépészmérnöki Kar, Műszaki Mechanikai Tanszék

Témavezető: Dr. Zelei Ambrus Miklós

Nemlineáris dinamikai és izommodellek az emberi helyváltoztatás biomechanikájában

A kutatási téma néhány soros bemutatása

Kutatásom során az emberi futás, ugrálás egyszerű mechanikai modellekkel történő vizsgálatával foglalkozom. Nem csupán az emberi test modellezése jelent kihívást, de az emberi idegrendszer működésének figyelembevétele is. A problémát több irányból is meg lehet közelíteni. Az egyik irány szerint az emberi testet tömegekkel, rugókkal és csillapításokkal, az idegrendszer hatását pedig (időkésleltetett) visszacsatolásos szabályozóval modellezik [1,2]. A másik megközelítés mozgásszervi modelleket használ, mely esetben az emberi test nagy pontossággal van figyelembe véve, az irányítása izommodellekkel történik, melyek aktivációjának megállapítását mért EMG adatokkal való optimalizációval végzik [3]. A kutatásom során a két megközelítést kapcsolom össze, azaz kis szabadságfokú modellt vizsgálok, izommodell bevonásával. Ezáltal a modell egyszerű kezelhetősége megmarad, a paraméterek hatása könnyedén vizsgálható, viszont az izommodell által közelebb kerülhetünk valóságos rendszerhez, azaz az emberhez, mint a tömeg-rugó modellek használata esetében.

A kutatóhely rövid bemutatása

A kutatást a BME Műszaki Mechanikai Tanszékén végzem. Ezenkívül tagja vagyok a 2022 őszén indult MTA-BME Lendület Globális Dinamika Kutatócsoportnak, mely nemlineáris problémákkal foglalkozik. A kutatócsoporton belül fejlesztett, és fejlesztendő módszereket, mint például a stabilitás, robusztusság, illetve a bifurkációk vizsgálatára használható algoritmusok, hasznosítani tudom a doktori kutatásomban.

A kutatás történetének, tágabb kontextusának bemutatása

Az emberi mozgás megértése napjainkban is fontos és kutatott téma. A felhasznált eredményeket szerteágazóan fel lehet használni orvosi diagnosztikától, rehabilitációtól kezdve (humanoid) robotok tervezésén át, a számítógépes játékok karaktereinek mozgástervezéséig. Az embert leíró modell választása nagyban függ attól, hogy milyen eredményeket szeretnénk kinyerni, azokat hol szeretnénk felhasználni.

Az emberi mozgás vizsgálatára különböző bonyolultságú modellek léteznek. Prediktív számításokhoz, az emberi mozgástervezés alapkutatásához az egyszerűbb, tömeg-rugó modelleket használják [1,2]. A modell egyszerűbb felépítéséből adódóan könnyebb az egyes paraméterek hatását vizsgálni ezek segítségével. Előnye, hogy kevesebb a számításigénye a szimulációknak.

A mozgás biomechanikai paramétereinek vizsgálatára minél emberhűbb modelleket szoktak használni, melyek mérések kiértékelésében segítenek [6]. A mozgásszervi modellek esetében Hill-féle izommodellek a legelterjedtebbek, melyek egy-egy izomcsoportot modelleznek. Az izmok mechanikai munkáját az izommodellek abszolút teljesítményének integráljával becsülik [7].

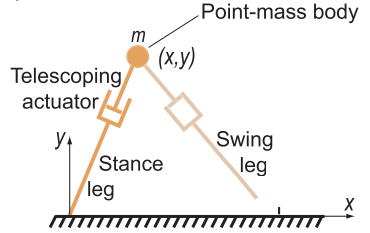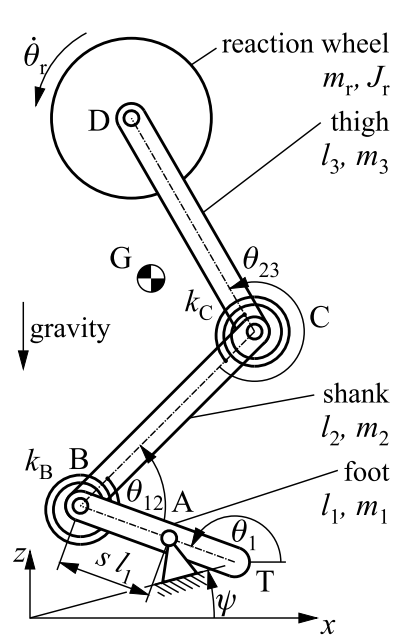a)    b)    c)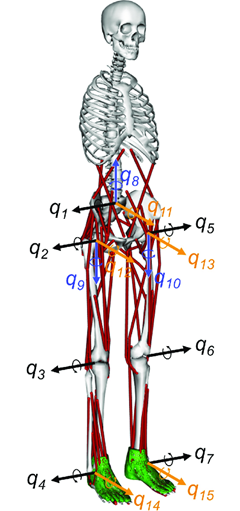

1. ábra: Különböző modellek az emberi test leírására: a) kéttámaszú tömeg-rugó inverz inga [4] b) többszegmensű láb [5] c) mozgásszervi modell [6]

 

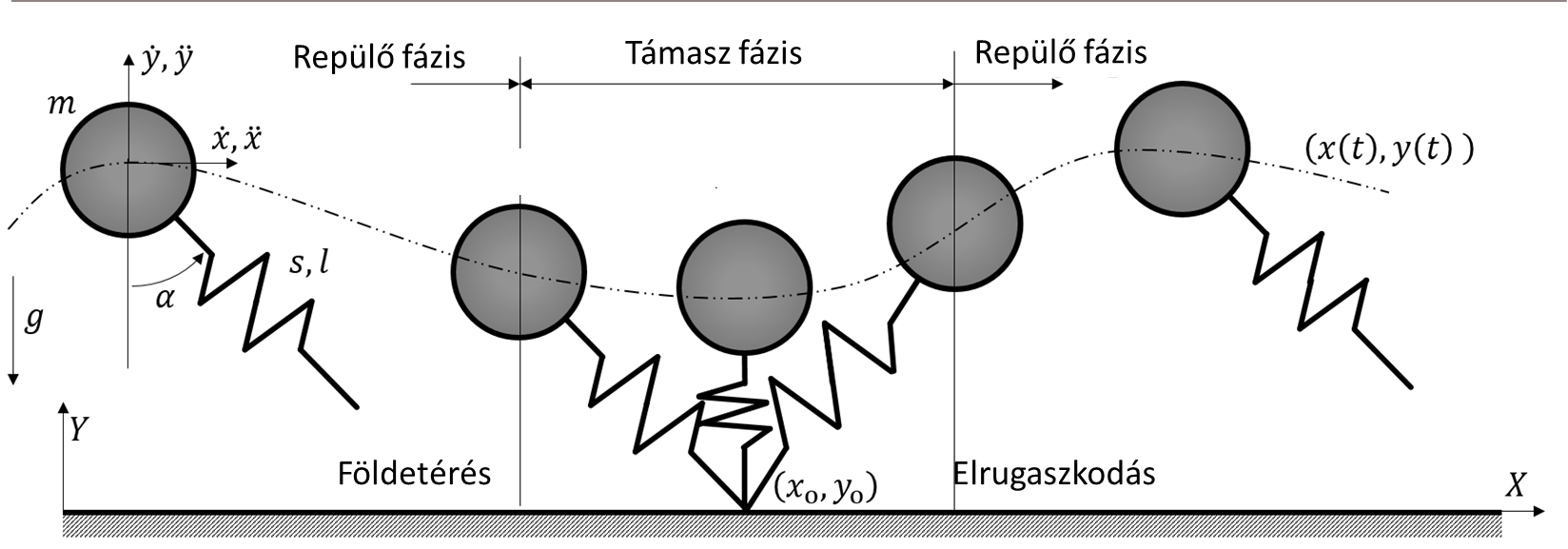
A kutatásom során a két megközelítés hozom össze; egyszerű mechanikai modellt vizsgálok, melyet Hill-izommal látok el. A mechanikai modell a szakirodalomban széles körben használt tömeg-rugó inverz inga modell, mely jól tudja közelíteni az emberi tömegközéppont mozgását ugrálás, szökdelés vagy futás esetén [3,8].

 

 

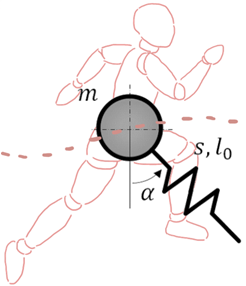
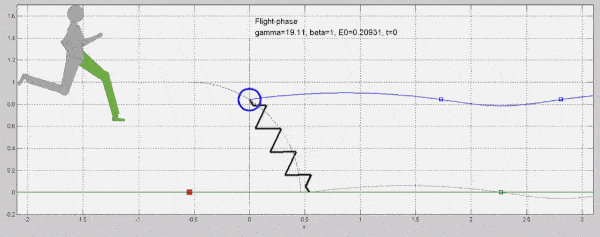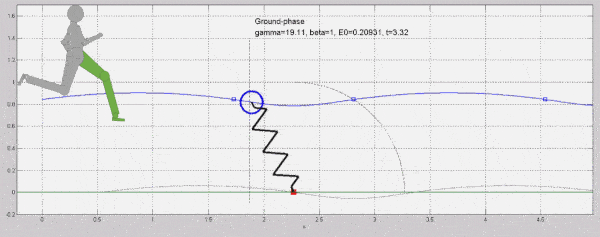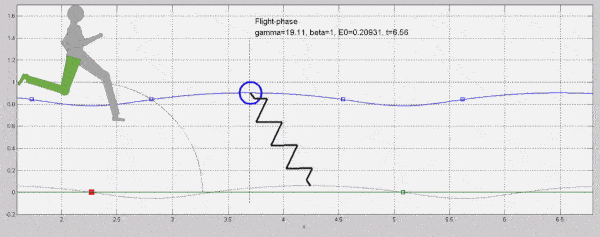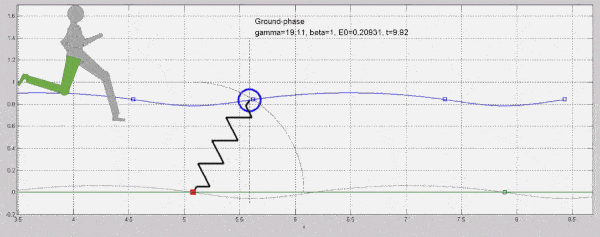
2. ábra: A tömeg-rugó/izom inverz inga modell egyszer az egyik, majd a másik lábat modellezi. Az adott fázisban modellezett láb zölddel jelölt.

A kutatás célja, a megválaszolandó kérdések.

A kutatás alapkutatás, melynek eredményeit az orvosi diagnosztika, illetve robotika területein lehet felhasználni. Azokra a kérdésekre keressük a választ, hogy milyen alapelvek szerint működhet az emberi mozgástervezés, illetve, hogy a különböző paramétereknek milyen hatása van a stabilitásra, dinamikai robusztusságra, valamint az energiafelhasználásra?

Miből ered a rendszer stabilitása? Hogyan lehet növelni a robusztusságot, hogy a rendszer jobban ellenálljon a külső zavarásokkal szemben? Milyen paraméterek választása követeli a legkevesebb befektetett energiát?

Nem célunk az emberi mozgást teljes egészében visszaadni; annak csupán bizonyos jellemzőit közelítjük. Megvizsgáljuk, hogy mik a használt mechanikai modell korlátjai, azaz az emberi futás, ugrálás milyen biomechanikai jellemzőit képes, illetve nem képes a modell visszaadni – például a tömegközéppont oszcillációja, periódusidő, lépésciklus hossza.

Módszerek

A kutatásom során először inverz kinematikával foglalkozom, mely átjárást biztosít a kis és nagy szabadságfokú modellek között abban az értelemben, hogy lehetővé teszi az inverz inga modellel prediktíven előállított pálya lekövetését többszegmensű modell által. Mivel az emberi láb redundáns, azaz a tömegközéppont egy helyzete végtelen sok lábszegmens-kombinációval visszakapható, a feladat nem triviális. A szakirodalomban több inverz kinematikai módszer létezik, melyek segítségével a feladat megoldható [9].

Mérések segítségével összehasonlítjuk, hogy amennyiben kézben tartott rúd végével való pályakövetés a cél, mely inverz kinematikai módszer adja vissza leginkább a megvalósult emberi mozgást. Ezáltal képet kapunk róla, vajon mi alapján szabályoz az emberi agy.

A futás, ugrálás leírására használt mechanikai modellt, mely a 2. ábrán volt látható, különböző módszerekkel vizsgálom. Amennyiben a probléma visszavezethető egy dimenziósra, a stabilitást és dinamikai robusztusságot elegendő Poincaré-féle visszatérési térképen vizsgálni, mely szemléletesen mutatja a rendszer viselkedését.

 

 

3. ábra: Baloldalt: Poincaré-féle visszatérési térkép: azt láthatjuk, milyen magasra ugrik fel a tömegpont a következő repülő fázisban. A különböző színek más mechanikai energiaszintnek felelnek meg, külső beavatkozás nélkül nincs köztük átjárás.

 

Bonyolultabb rendszerek esetén a stabilitást a monodrómia mátrix sajátértékeinek vizsgálatával elemzem, a rendszer robusztusságát pedig a dinamikai integritással becsülöm [10]. A helyi integritás mérőszámának számításához a DynIn Toolboxot használom, melyet az MTA-BME Lendület Globális Dinamika Kutatócsoporton belül fejlesztünk.

A Hill-izommodell esetében csak az összehúzó elemet veszem figyelembe, mely az izommodell aktív eleme, az izom és az ínak passzív rugalmasságát elhanyagolom. A Hill-izom rendelkezik belső nemlineáris erő–hossz és erő–sebesség karakterisztikával. Ez azt jelenti, hogy a modell figyelembe veszi, hogy a maximálisan kifejtendő erő függ az izom aktuális hosszától, és annak összehúzódási gyorsaságától. Ezeket a nemlineáris összefüggéseket lehet lineárisan közelíteni, illetve elhanyagolni, amennyiben konstansnak választjuk. A szabályozást az időtől függő aktivációs szinten keresztül vehetjük figyelembe, mely azt jellemzi, hogy mennyire szeretnénk megfeszíteni az izmunkat.

 

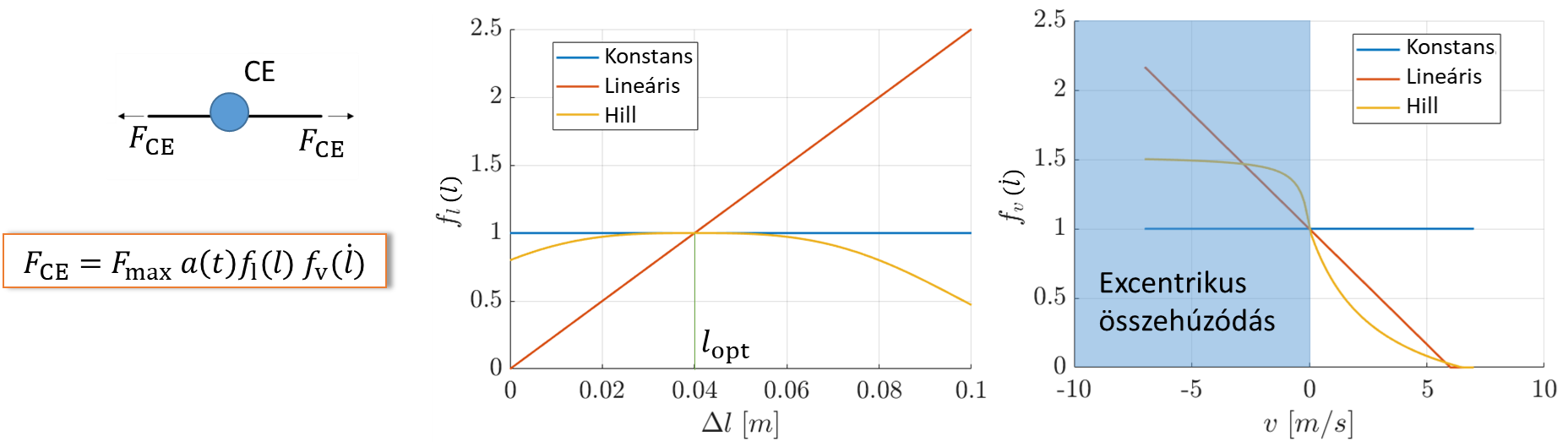
4. ábra: Hill-izom által kifejtett erőt befolyásoló jellemzők

 

Mérések segítségével hangolom az izommal szabályozott inverz inga modellt, és megfigyelem, hogy milyen bonyolultsággal szükséges figyelembe venni az izommodell belső karakterisztikáit, hogy megfelelő módon közelítsük a megvalósult mozgásformát.

Eddigi eredmények

Az emberi pályakövetéssel kapcsolatban azt az eredményt kaptuk, hogy amennyiben elhanyagolható a kézben tartott rúd tömege, az ember a karszegmenseivel a csuklótartományainak közepén igyekszik maradni. Nagyobb tömeg esetén a manipulálhatóságra maximalizál.

 

 

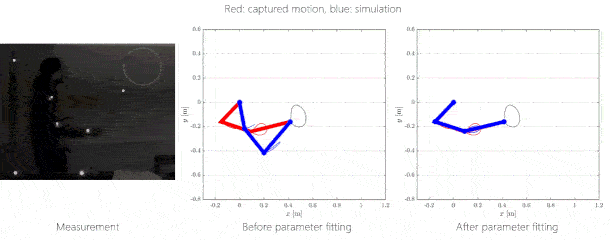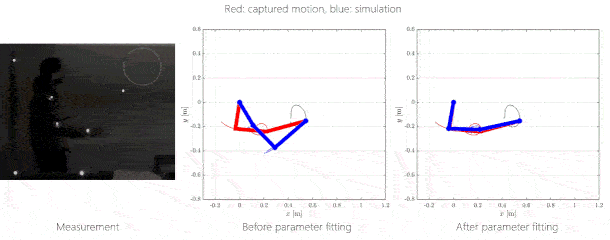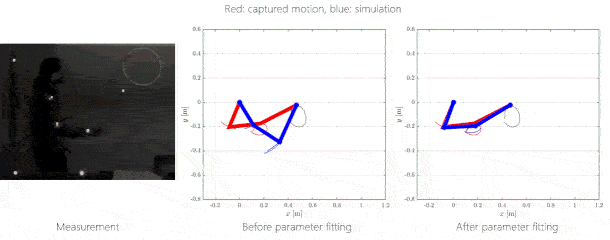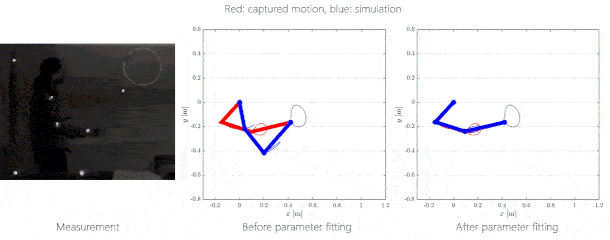
5. ábra: Pályakövetés inverz kinematikai feladat megoldásával. Jobboldalt: piros: mért emberi mozgás, kék: szimulált mozgás optimalizálás nélkül és optimalizálással.

 

Habár a tömeg-rugó inverz inga modell széles körben vizsgált rendszer, a teljes stabil paramétertartományát nem találtuk meg a szakirodalomban. Készítettünk MatLab környezetben egy demonstrációs eszközt, mely megmutatja, hogy tetszőleges dimenziótlan paraméterek választása esetén hol helyezkedünk el a paramétertérben a stabil tartományhoz képest.

Az egyhelyben való ugrálás esetében feedforward vezérlést használtam, melynek fiziológiai háttere a központi mintagenerátor, melynek központja a gerincben található, és periodikus jeleket küld az izmok felé. Azért éltem ezzel a megközelítéssel, mivel monoton ugrálás esetén nincs különösebb szükség a mozgásba való tudatos beavatkozásba. A mechanikai modellemnek hat különböző bonyolultságú rendszerét vizsgáltam, az izommodell erő-hossz és erő-sebesség karakterisztikáinak különböző módon való figyelembevételével. Az aktivációs szintet úgy választottam meg, hogy az erőlefutás időben szimmetrikus legyen. Az eredményeimet összehasonlítottam a szakirodalomban megtalálható hasonló modellel, melynek aktivációs szintjét genetikus algoritmussal határozták meg [11]. Mindegyik rendszer képes volt aszimptotikusan stabil periodikus mozgásra. A szimmetrikus erőlefutás esetében az izom úgy viselkedett, mint egy rugó a periodikus pályán való mozgás során, így jobb energiafelhasználással rendelkezett, mint a [11]-ben található rendszerek. Másrészről alacsonyabbra tudott ugrani, illetve kevésbé ellenálló a külső zavarásoknak. A hatféle rendszer közül a legrosszabbul a lineáris-lineáris erő-hossz és erő-sebesség összefüggéssel rendelkező rendszer teljesített.

Várható impakt, további kutatás

A kutatás során levont következtetések robotok tervezésénél hasznosak, mind aktuátorok választásánál, mind azok szabályozásának tervezésénél. Orvosi diagnosztikában is használhatók az eredmények, hiszen a modell egyszerűségéből adódóan kevés mérési ponttal hangolható, így bizonyos biomechanikai jellemzők gyorsabban kiszámíthatók. A robusztusság vizsgálatára kidolgozott módszerek általánosabban is hasznosíthatóak lehetnek más nemlineáris rendszer vizsgálatára akár iparban dolgozó mérnökök, akár kutatók számára. További kutatás keretein belül a modell kiegészíthető több izommodellel, vagy szegmenssel, a pontosabb eredmények elérése érdekében.

Saját publikációk, hivatkozások, linkgyűjtemény

Kapcsolódó saját publikációk listája:

[S1] Dóra Patkó, Ambrus Zelei: Kinematic Redundancy Resolution in Robotics and in Human Motion - An Experimental Case Study. The Fourth Joint International Conference on Multibody System Dynamics - IMSD 2016, Montreal, Kanada, május 29–június 2.

[S2] Patkó Dóra, Zelei Ambrus: A poszturális egyensúlyozás és a futás stabilizációjához felhasznált energiamennyiség viszonyának becslése. XXVII. Nemzetközi Gépészeti Konferencia – OGÉT, Nagyvárad, Románia, 2019. április 25–28., ISSN 2068-1267

[S3] Ambrus Zelei, Dóra Patkó: Alternative inverse kinematic calculation methods in velocity and acceleration level. In: Theoretical Approaches in Non-Linear Dynamical Systems, (2019) pp. 405–418, ISBN 978-83-66287-29-7

[S4] Dóra Patkó, Ambrus Zelei: Velocity and acceleration level inverse kinematic calculation alternatives for redundant manipulators. In: Meccanica - An International Journal of Theoretical and Applied Mechanics AIMETA, (2021), 56(4), pp. 887–900

[S5] Dóra Patkó, Ambrus Zelei: Egyszerűsített Hill-izommodell használata tömeg-rugó modellel - lehetséges az aszimptotikus stabilitás? 8. Magyar Biomechanikai Konferencia, Online, 2021. április 09. In: Biomechanica Hungarica Különkiadás, (2021) 14(1) pp. 22–23

[S6] Ábel Mihály Nagy, Dóra Patkó, Ambrus Zelei: Discovery and Online Interactive Representation of the Dimensionless Parameter-Space of the Spring-Loaded Inverted Pendulum Model of Legged Locomotion Using Surface Interpolation. 16th International Conference on Dynamical Systems, Theory and Applications (DSTA 2021), 2021. december 6–9., Online. doi.org/10.34658/9788366741201

[S7] Dóra Patkó, Ambrus Zelei: Numerical stability analysis of the conservative SLIP model with a Hill-type muscle. ECCOMAS Thematic Conference on Multibody Dynamics December 12–15, 2021, Online

[S8] Patkó Dóra, Nagy Ábel Mihály, Zelei Ambrus: A futás és szökdelés tömeg-rugó modell dinamikai viselkedésének globális feltérképezése és paraméterhangolása. In: Biomechanica Hungarica, (2022) 15(1) pp. 39–50

[S9] Dóra Patkó, Ambrus Zelei: Symmetry, benefit or disadvantage? Energy consumption of simple hopping model with intrinsic muscle properties. 6th International Conference of Dynamic, Vibration and Control (ICDVC 2022+1) 2023. április 7–9.

[S10] Dóra Patkó, Ambrus Zelei, Giuseppe Habib: Comparison of feed-forward control strategies for hopping model with intrinsic muscle properties of different complexities. Third International Nonlinear Dynamics Conference (NODYCON 2023) Róma, Olaszország, 2023. június 18–22.

[S11] Ábel Mihály Nagy, Dóra Patkó, Ambrus Zelei: Discovery and Interactive Representation of the Dimensionless Parameter-Space of the Spring-Loaded Inverted Pendulum Model of Legged Locomotion Using Surface Interpolation. In: Springer Proceedings in Mathematics & Statistics (2023) (elfogadott)

 

Linkgyűjtemény:

Tömeg-rugó inverz inga interaktív dimenziótlan stabilitási térképe

Műszaki Mechanikai Tanszék

MTA-BME Lendület Globális Dinamika Kutató Csoport

Tanszéki honlapom

MTMT

Google Scholar

ResearchGate

 

Hivatkozások listája:

[1] Csenge A Molnar, Tamas Balogh, Islam Boussaada, Tamas Insperger: Calculation of the critical delay for the double inverted pendulum. Journal of Vibration and Control (2021) 27(3–4) pp 356–364.

[2] Nikooyan AA, Zadpoor AA.: Mass-spring-damper modelling of the human body to study running and hopping--an overview. Proceedings of the Institution of Mechanical Engineers, Part H: Journal of Engineering in Medicine (2011) 225(12) pp. 1121–35.

[3] H. Geyer, A. Seyfarth: Neuromuscular Control Models of Human Locomotion. Humanoid Robotics: A Reference (2017)

[4] M. Srinivasan, A. Ruina: Computer optimization of a minimal biped model discovers walking and running. (2006) Nature 439(7072) pp. 72–75

[5] A. Zelei, B. Krauskopf, P.T. Piiroinen, T. Insperger: Stable periodic motion of a controlled segmented leg model of pedal locomotion with inelastic ground-foot collision. (2019) Nonlinear Dynamics 97(3) pp. 1945–1958.

[6] Kaminishi K, Jiang P, Chiba R, Takakusaki K, Ota J: Postural control of a musculoskeletal model against multidirectional support surface translations. (2019) PLoS ONE 14(3)

[7] K. Sasaki, R.R. Neptune, S.A. Kautz: The relationships between muscle, external, internal and joint mechanical work during normal walking. (2009) Journal of Experimental Biology 212(5) pp. 738–744

[8] M. Hutter, D.C. Remy, M.A. Hopflinger, R. Siegwart: SLIP running with an articulated robotic leg. International Conference on Intelligent Robots and Systems, Taipei, TAIWAN, 2010. október 18–22.

[9] J. Hollerbach, K. Suh: Redundancy resolution of manipulators through torque optimization. In: IEEE Journal on Robotics and Automation, (1987) 3(4), pp. 308–316.

[10] G. Habib: Dynamical integrity assessment of stable equilibria: a new rapid iterative procedure. (2021) Nonlinear Dynamics 106(3) pp. 2073–2096.

[11] Haeufle, D. F.B., Grimmer, S., Seyfarth, A.: The role of intrinsic muscle properties for stable hopping - Stability is achieved by the force-velocity relation. (2010) Bioinspiration and Biomimetics 5(1)