Géza Pattantyús-Ábrahám Doctoral School of Mechanical Engineering 

BME Faculty of Mechanical Engineering, Department of Applied Mechanics

Supervisor: Dr. Zelei Ambrus Miklós

Nonlinear dynamical and muscle models in the human locomotion

Introducing the research area

In my research, I study human running and jumping using simple mechanical models. The challenge is not only to model the human body but also to consider the functioning of the human nervous system. The problem can be approached from several directions. One approach is to model the human body with masses, springs, and dampers, and the action of the nervous system with a (time-delayed) feedback controller [1,2]. The other approach uses musculoskeletal models, in which the human body is considered with high accuracy, controlled by muscle models, whose activation level is determined by optimizing measured EMG data [3]. In my research, I combine the two approaches, i.e., I investigate a low degree of freedom model with a muscle model. In this way, the ease of use of the model is preserved, and the effect of the parameters can be easily investigated, but the muscle model allows us to get closer to a real system, namely a human, than when using mass-spring-damper models.

Brief introduction of the research place

The research is carried out at the BME, Department of Applied Mechanics. In addition, I am a member of the MTA-BME Lendület Global Dynamics Research Group, which was started in autumn 2022 and is working on nonlinear problems. Methods developed and to be developed within the research group can be used in my PhD research, such as algorithms for stability, robustness, and bifurcations.

History and context of the research

Understanding human motion is still an important and researched topic. The results can be used in various fields, ranging from medical diagnostics and rehabilitation to the design of (humanoid) robots and the motion design of characters in computer games. The choice of the model to describe a human depends largely on the results we want to obtain and where we want to use them.

There are models of varying complexity for studying human movement. For predictive calculations, for basic research on human motion planning, simpler, mass-spring-damper models are used [1,2]. Because of the simpler model structure, it is easier to investigate the effects of certain parameters using these models. This has the advantage that simulations have less computational demand.

To investigate the biomechanical parameters of the motion, it is common to use models that are as human-like as possible to help in the evaluation of the measurements [6]. In the case of musculoskeletal models, Hill's muscle models are the most common, which model a single muscle group. The mechanical work of the muscles is estimated by integrating the absolute power of the muscle models [7].

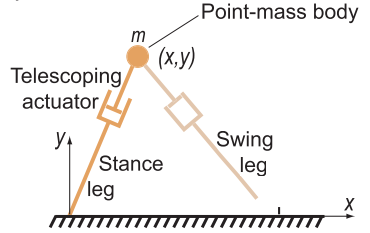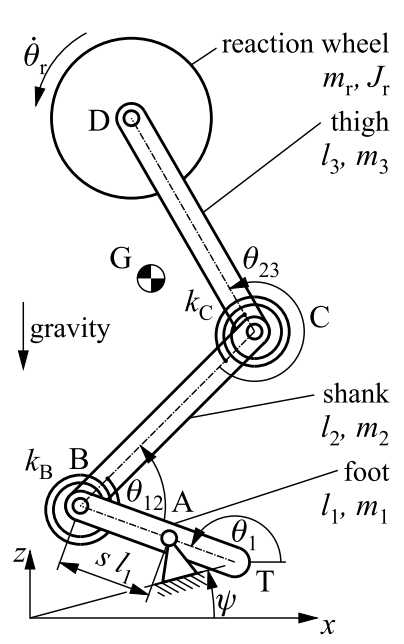a)    b)    c)

1. figure: Different models for describing the human body: a) double-supported spring-loaded inverted pendulum [4] b) multi-segmented leg [5] c) musculoskeletal model [6].

 

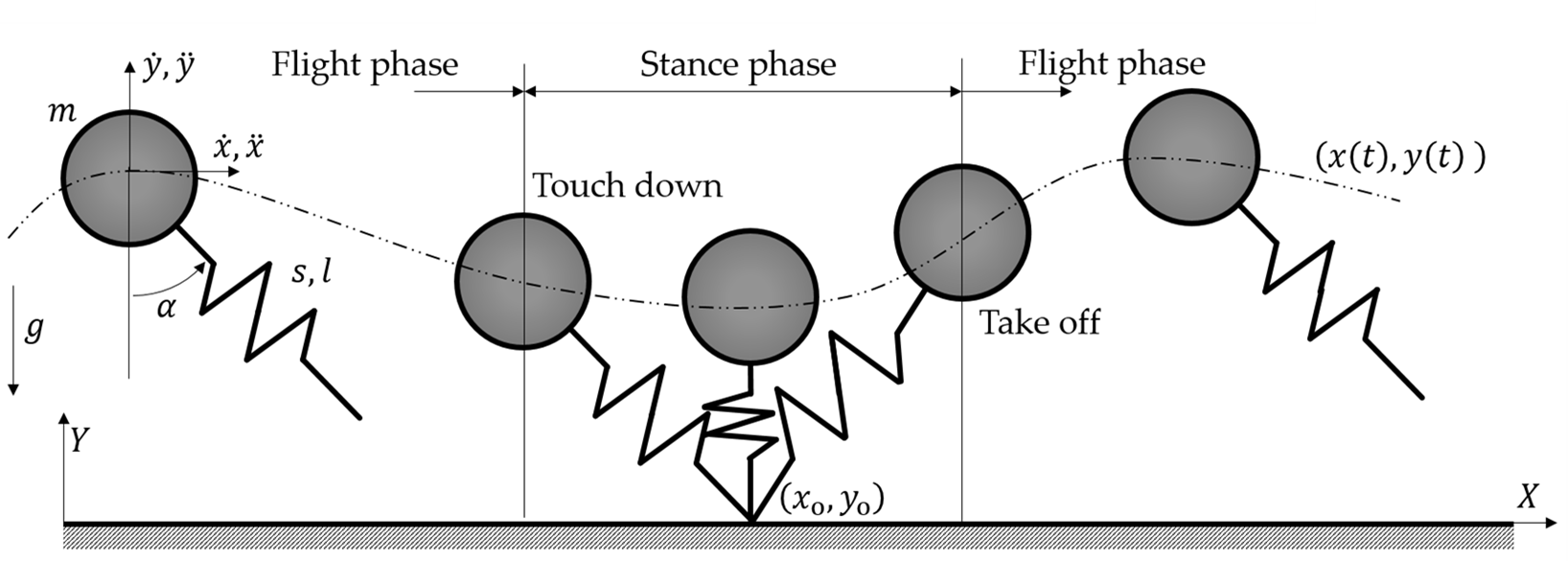
In my research I combine the two approaches; I investigate a simple mechanical model with a Hill muscle. The mechanical model is the spring-loaded inverted pendulum (SLIP) model, widely used in the literature, which can accurately approximate the motion of the human center of mass when jumping, hopping, or running [3,8].

 

 

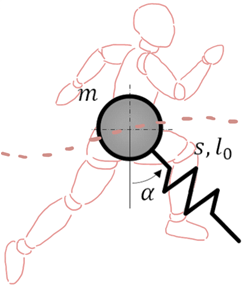
2. figure: The SLIP model; the spring/muscle represents one leg alternately. The leg modeled in a given phase is marked by green.

The research goals, open questions

The work is basic research, the results of which can be used in the fields of medical diagnostics and robotics. The questions to be answered are the principles of human motion planning and the impact of different parameters on stability, dynamic robustness, and energy consumption.

Where does the stability of a system come from? How can robustness be increased to make the system more resistant to external disturbances? Which parameter choices require the least energy investment?

We do not aim to reproduce human motion in its entirety, merely to approximate certain aspects of it. We will investigate the limitations of the mechanical model used, i.e., what biomechanical characteristics of human running and jumping can or cannot be reproduced, for example, oscillation of the center of mass, period time, and step cycle length.

Methods

First, my research deals with inverse kinematics, which provides a transition between low and high degrees of freedom models. In other words, it allows the trajectory that was predictively generated by the inverted pendulum model to be tracked by a multi-segment model. Since the human leg is redundant, i.e., a position of the center of mass can be retrieved by an infinite number of leg segment combinations, the task is non-trivial. Several inverse kinematics methods exist in the literature to solve the problem [9].

Measurements are used to compare which inverse kinematics method reproduces the realized human motion best when tracking with the end of a hand-held rod. This will give us an idea of the basis on which the human brain controls.

The mechanical model used to describe running and jumping, shown in Figure 2, is investigated using different methods. If the problem can be reduced to one dimension, stability, then dynamic robustness can be investigated using a Poincaré return map, which gives a visual representation of the system behavior.

 

 

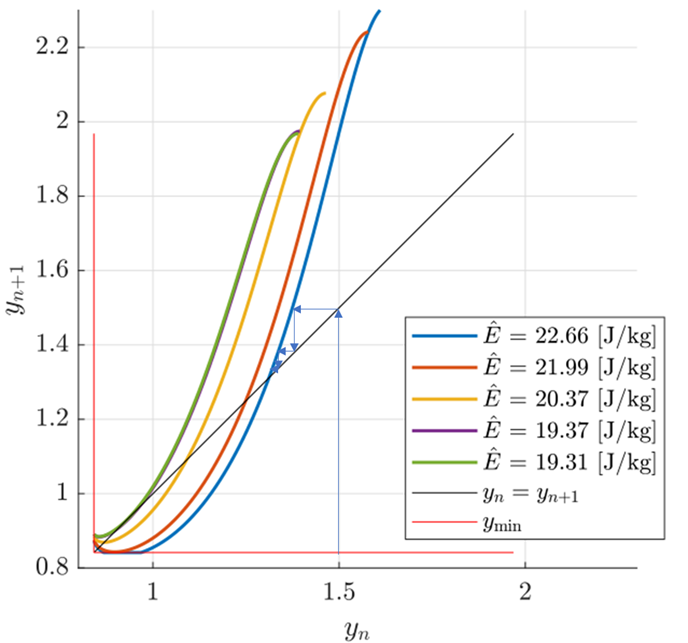
3. figure: Left: Poincaré return map: showing how high the center of mass will jump in the next flight phase.
The different colors correspond to different mechanical energy levels. Without any external excitation, there is no transition between them.

 

In the case of more complex systems, the stability investigation is carried out by examining the eigenvalues of the monodromy matrix, while the robustness of the system is estimated by the dynamical integrity. To calculate the local integrity measure I use the DynIn Toolbox, which is currently under development by the MTA-BME Lendület Global Dynamics Research Group.

For the Hill muscle model, I only consider the contractile element, which is the active element of the muscle model, and neglect the passive elasticity of the muscle and tendons. The Hill muscle has intrinsic nonlinear force-length and force-velocity characteristics. This means that the model considers that the maximum force that can be exerted depends on the actual length of the muscle and its contraction velocity. These nonlinear relationships can be approximated linearly or neglected if chosen as constants. The control can be considered through the time-dependent activation level, which characterizes how much we want to tighten our muscles.

 

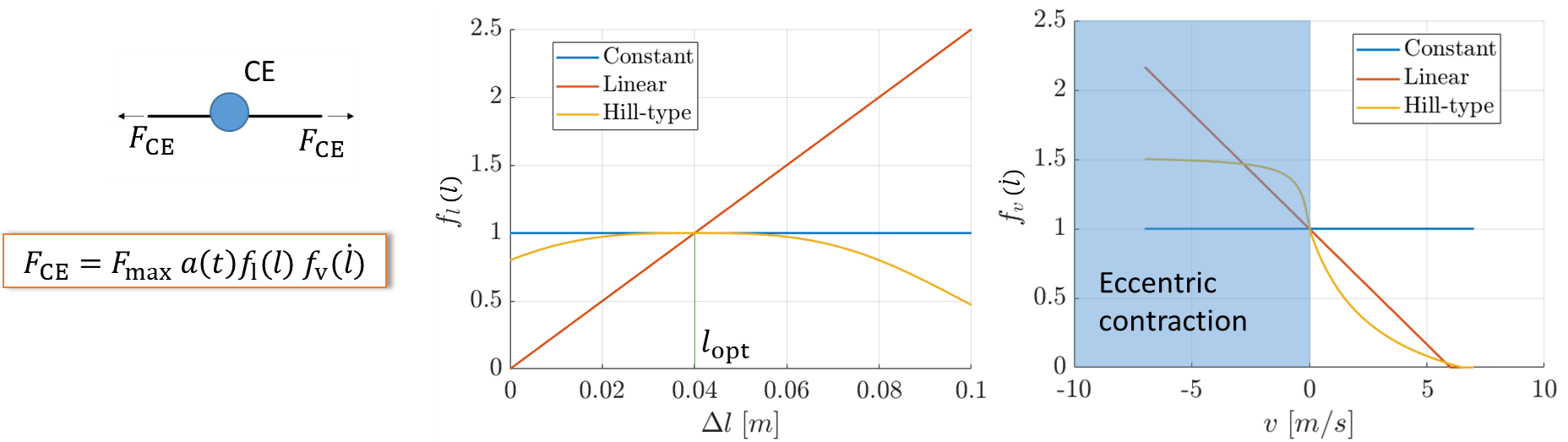
4. figure: Characteristics affecting the force exerted by the Hill-type muscle.

 

I use measurements to tune the muscle-controlled inverted pendulum model and observe the complexity required to account for the intrinsic properties of the muscle model to adequately approximate the realized motion.

Results

For human path tracking, the result is that, if the mass of the rod in the hand is negligible, humans tend to keep the joints of the arm in the middle of their joint spans. For higher mass, manipulability is maximized.

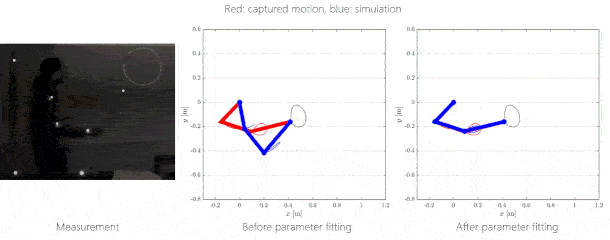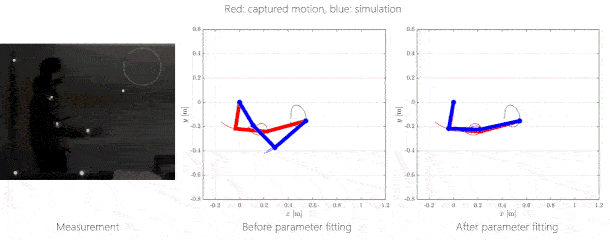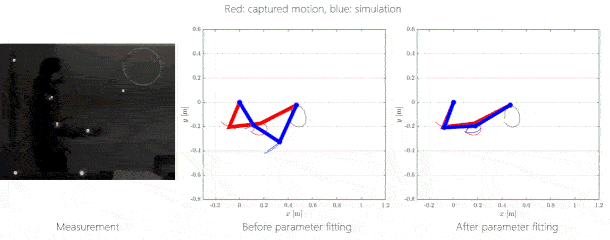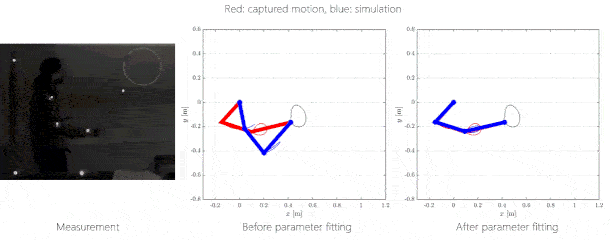
5. figure: Trajectory tracking by solving the inverse kinematics problem.
Right: red: measured human motion, blue: simulated motion without and with optimization.

 

Although the SLIP model is a widely studied system, its complete stable parameter map has not been found in the literature. We have created a demonstration tool in the MatLab environment to show where we are in the parameter space relative to the stable range for an arbitrary choice of dimensionless parameters.

For modeling hopping motion, feedforward control is used. Its physiological background is the central pattern generator found in the spinal cord, which sends periodic signals to the muscles. I used this approach because, in the case of monotonic hopping, there is no particular need for conscious intervention in the movement. I have investigated six systems of different complexity of the mechanical model, with different considerations of the force-length and force-velocity characteristics of the muscle model. The activation level was chosen such that the force-time history is symmetric in the stance phase during periodic motion. I compared my results with similar models in the literature, whose activation levels were determined by a genetic algorithm [11]. All systems were capable of asymptotically stable periodic motion. For the systems with symmetric force-time history, the muscle behaved like a spring during periodic motion and thus had better energy consumption properties than the systems in [11]. On the other hand, they could jump lower and were less resistant to external perturbations. Of the six systems, the ones with the linear-linear force-length and force-velocity relations performed the worst.

Expected impact and further research

The conclusions drawn from this research are useful for the design of robots, both in the choice of actuators and in the design of their control. The results can also be used in medical diagnostics, since due to the simplicity of the model, a few measurement points are needed to tune it, allowing certain biomechanical properties to be calculated more quickly. The methods developed for robustness testing are general and can be used on nonlinear systems, either by engineers working in industry or by researchers. In the context of further research, the model can be extended to include more muscle models or segments in order to achieve more accurate results.

Publications, references, links

List of corresponding own publications:

[S1] Dóra Patkó, Ambrus Zelei: Kinematic Redundancy Resolution in Robotics and in Human Motion - An Experimental Case Study. The Fourth Joint International Conference on Multibody System Dynamics - IMSD 2016, Montréal, Canada, May 29–June 2.

[S2] Patkó Dóra, Zelei Ambrus: A poszturális egyensúlyozás és a futás stabilizációjához felhasznált energiamennyiség viszonyának becslése. XXVII. Nemzetközi Gépészeti Konferencia - OGÉT, Oradea, Romania, April 25–28, 2019, ISSN 2068-1267

[S3] Ambrus Zelei, Dóra Patkó: Alternative inverse kinematic calculation methods in velocity and acceleration level. In: Theoretical Approaches in Non-Linear Dynamical Systems, (2019) pp. 405–418, ISBN 978-83-66287-29-7

[S4] Dóra Patkó, Ambrus Zelei: Velocity and acceleration level inverse kinematic calculation alternatives for redundant manipulators. In: Meccanica - An International Journal of Theoretical and Applied Mechanics AIMETA, (2021), 56(4), pp. 887-900

[S5] Dóra Patkó, Ambrus Zelei: Egyszerűsített Hill-izommodell használata tömeg-rugó modellel - lehetséges az aszimptotikus stabilitás? 8. Magyar Biomechanikai Konferencia, Online, April a9, 2021. In: Biomechanica Hungarica Special issue, (2021) 14(1) pp. 22–23

[S6] Ábel Mihály Nagy, Dóra Patkó, Ambrus Zelei: Discovery and Online Interactive Representation of the Dimensionless Parameter-Space of the Spring-Loaded Inverted Pendulum Model of Legged Locomotion Using Surface Interpolation. 16th International Conference on Dynamical Systems, Theory and Applications (DSTA 2021), December 6-9, 2021, Online. doi.org/10.34658/9788366741201

[S7] Dóra Patkó, Ambrus Zelei: Numerical stability analysis of the conservative SLIP model with a Hill-type muscle. ECCOMAS Thematic Conference on Multibody Dynamics December 12-15, 2021, Online

[S8] Patkó Dóra, Nagy Ábel Mihály, Zelei Ambrus: A futás és szökdelés tömeg-rugó modell dinamikai viselkedésének globális feltérképezése és paraméterhangolása. In: Biomechanica Hungarica, (2022) 15(1) pp. 39–50

[S9] Dóra Patkó, Ambrus Zelei: Symmetry, benefit, or disadvantage? Energy consumption of simple hopping model with intrinsic muscle properties. 6th International Conference of Dynamic, Vibration and Control (ICDVC 2022+1) April 7–9, 2023.

[S10] Dóra Patkó, Ambrus Zelei, Giuseppe Habib: Comparison of feed-forward control strategies for hopping model with intrinsic muscle properties of different complexities. Third International Nonlinear Dynamics Conference (NODYCON 2023) Rome, ITALY, 2023. June 18–22.

[S11] Ábel Mihály Nagy, Dóra Patkó, Ambrus Zelei: Discovery and Interactive Representation of the Dimensionless Parameter-Space of the Spring-Loaded Inverted Pendulum Model of Legged Locomotion Using Surface Interpolation. In: Springer Proceedings in Mathematics & Statistics (2023) (accepted)

 

Table of links:

Interactive dimensionless parameter map for the SLIP model

Department of Applied Mechanics

Global Dynamics Research Group

Professional website

MTMT

Google Scholar

ResearchGate

 

List of references:

[1] Csenge A Molnar, Tamas Balogh, Islam Boussaada, Tamas Insperger: Calculation of the critical delay for the double inverted pendulum. Journal of Vibration and Control (2021) 27(3-4) pp 356–364.

[2] Nikooyan AA, Zadpoor AA.: Mass-spring-damper modelling of the human body to study running and hopping--an overview. Proceedings of the Institution of Mechanical Engineers, Part H: Journal of Engineering in Medicine (2011) 225(12) pp. 1121–35.

[3] H. Geyer, A. Seyfarth: Neuromuscular Control Models of Human Locomotion. Humanoid Robotics: A Reference (2017)

[4] M. Srinivasan, A. Ruina: Computer optimization of a minimal biped model discovers walking and running. (2006) Nature 439(7072) pp. 72–75

[5] A. Zelei, B. Krauskopf, P.T. Piiroinen, T. Insperger: Stable periodic motion of a controlled segmented leg model of pedal locomotion with inelastic ground-foot collision. (2019) Nonlinear Dynamics 97(3) pp. 1945–1958.

[6] Kaminishi K, Jiang P, Chiba R, Takakusaki K, Ota J: Postural control of a musculoskeletal model against multidirectional support surface translations. (2019) PLoS ONE 14(3)

[7] K. Sasaki, R.R. Neptune, S.A. Kautz: The relationships between muscle, external, internal, and joint mechanical work during normal walking. (2009) Journal of Experimental Biology 212(5) pp. 738–744

[8] M. Hutter, D.C. Remy, M.A. Hopflinger, R. Siegwart: SLIP running with an articulated robotic leg. International Conference on Intelligent Robots and Systems, Taipei, TAIWAN, 2010. October 18–22.

[9] J. Hollerbach, K. Suh: Redundancy resolution of manipulators through torque optimization. In: IEEE Journal on Robotics and Automation, (1987) 3(4), pp. 308–316.

[10] G. Habib: Dynamical integrity assessment of stable equilibria: a new rapid iterative procedure. (2021) Nonlinear Dynamics 106(3) pp. 2073–2096.

[11] Haeufle, D. F.B., Grimmer, S., Seyfarth, A.: The role of intrinsic muscle properties for stable hopping - Stability is achieved by the force-velocity relation. (2010) Bioinspiration and Biomimetics 5(1)