|
|
BMe Kutatói pályázat |
|
Oláh György Doktori Iskola
Kémiai és Környezeti Folyamatmérnöki Tanszék
Témavezető: Dr. Szilágyi Botond
Digitális eszközök fejlesztése műszaki kristályosítási folyamatok tervezéséhez és szintéziséhez
A kutatási téma néhány soros bemutatása
Kutatásom fő iránya egy vegyiparban nagy jelentőséggel bíró technológiai folyamathoz, a kristályosításhoz kötődő matematikai modellezési módszerek fejlesztése. Ezen módszerek olyan irányú fejlesztését tűztem ki célul, melyek közvetlenül alkalmazhatók az iparban felmerülő gyakorlati kérdések megválaszolására. Munkám a gyógyszerhatóanyagok, élelmiszeripari termékek, műtrágyák mellett még sok más termék előállítását teheti biztonságosabbá, gyorsabbá és olcsóbbá.
A kutatóhely rövid bemutatása
Kutatásomat a Műegyetemen frissen megalakult Kristályosítási és Folyamatmérnöki Kutatócsoportban végzem. Csoportunk kristályosítási és más vegyipari technológiai folyamatok szabályozásával, mélyebb megértésével és optimalizálásával foglalkozik a számítástechnika legkorszerűbb eszközeinek felhasználásával. Ebben a matematika, kémia és informatika tudományágait átfogó nagyon izgalmas multidiszciplináris működési formában keressük az ipari gyakorlatban hasznosítható megoldásokat.
A kutatás történetének, tágabb kontextusának bemutatása
A kristályosítás az egyik legszélesebb körben alkalmazott vegyipari technológia, melyet elválasztásra és tisztításra rutinszerűen alkalmaznak a gyógyszeripartól az élelmiszeriparon át a robbanószergyártásig. Ennek a nagy múltú technológiának azonban különösen nagy jelentősége van például a gyógyszeriparban, ahol a folyamat precíz megtervezésével a végtermék feldolgozhatósága és biohasznosulása akár nagyságrendekkel javítható.[1] Ezen folyamatok pontos, számítógépes modellezés segítségével optimalizált megtervezésében sokat segíthetnek az utóbbi években, évtizedekben megjelent módszerek (populációmérleg-alapú modellek (PB), numerikus áramlástani (CFD), mesterséges intelligencia- (MI-) és adatelemzés-alapú módszerek stb.), melyekkel a kristályosítás gyorsabban, hatékonyabban, ezáltal olcsóbban történhet. [2,3] Az előbbiekben felsorolt módszerekkel szimulált kísérletekkel kiváltható a fizikai kísérletezés, az optimális gyártási körülmények gyorsabban megkereshetők, és a folyamatokra ható változókból megbízhatóbban következtethetünk a folyamataink javításához szükséges lépésekre. A fentiekből kiinduló PhD témámban a számítástechnikai eszközök olyan innovatív alkalmazásmódjait keresem, melyek gyorsabban, szabályozottabban és olcsóbban juttatják el a felhasználókhoz a számukra szükséges termékeket. Ezen keresztül az Ipar 4.0 és Quality by Design (QbD) alapelvek gyakorlatban történő megvalósításához is közelebb segíthetem az ipari szereplőket.
A kutatás célja, a megválaszolandó kérdések.
A kutatásomban alapvetően gyakorlati problémák megválaszolására szeretném alkalmazni azokat a korszerű matematikai modellezési módszereket, melyek más műszaki területen már kiállták az alkalmazhatóság próbáját. Ezen felül olyan új alkalmazási módokat keresek, melyek gyorsabbá és olcsóbbá tehetik az ipari gyártási folyamatok tervezési, optimalizálási vagy folyamatszabályozási fázisait. Harmadrészt pedig olyan eszközök fejlesztésén dolgozom, melyeket az iparban könnyen, gyakorlatiasan lehet használni, hogy minél kisebbre csökkenjen a tudományos újítások ipari felhasználását gyakorta gátló belépési küszöb. Kutatásaimban arra keresem a választ, hogy a PB-modellek felállítását, majd pedig gyakorlati alkalmazását, hogyan lehet hatékonyabban megoldani: szoftveresen vagy hagyományos módszerekkel? Mit tehetünk, ha kevés kiindulási adatunk van a modell felállításához? Végül, hogy a keverési viszonyok tulajdonságai milyen kapcsolatba hozhatók a léptéknövelés kristályméretre gyakorolt hatásával?
Módszerek
A kristályosítási folyamatok legelterjedtebb modellezési módszere a populációmérleg-alapú modellezés (PB), melynek segítségével szimulálhatjuk a rendszerünkben keletkező termék méretét, tisztaságát és egyéb tulajdonságait, és így gyorsabban és olcsóbban tudjuk a folyamatainkat tervezni, szabályozni és optimalizálni. A modellezési módszer kivitelezhető szoftveresen (kereskedelmi forgalomban lévő programok) vagy hagyományos matematikai modellezés (pl. Matlab© vagy Python©) útján. A PB-modellek felépítéséhez a kristályos termék méretén és a kristályosodó vegyület oldhatóságán kívül a folyamat alatti további adatra van szükség, amely vagy a koncentráció vagy pedig a kristályok számának és méretének változása. Adott valós gyártási folyamatban azonban ezek az adatok nem mindig érhetők el a szükséges számban, illetve minőségben, ami komoly gátja a módszer alkalmazásának. Ennek feloldására három kutatási témám épül a PB-modellezés köré: (1) ugyanazon kristályosítási folyamat modellezését szoftveresen (CrySiV) és hagyományosan is elvégzem, majd a két modellel in-silico kísérlettervet generálva és azokat kiértékelve mélységében hasonlítom össze a két modellezési megközelítés képességeit; (2) egy ipari léptékű kristályosítási folyamathoz többségében előre meglévő adatok segítségével PB-modellt építek (így maradva közel a gyakorlatiasság kritériumához), és a matematikai modellel ipari léptékű és laboros méretben is robusztus hőmérsékletprofil-optimalizációt hajtok végre. A harmadik, egyben utolsó témám a (3) keverési viszonyok és a kristályosítási folyamatok léptéknövelése közötti kapcsolat feltárása a gépészmérnöki tudományokban alkalmazott CFD-szimulációk és PLSR- (partial least squares regression) módszerek segítségével.
Eddigi eredmények
(1) Az első kutatási témám kidolgozása során sikerült bemutatnom a pregabalin hűtéses kristályosításának modellezésén keresztül, hogy a CrySiV folyamatszimulációs szoftverrel a hagyományos matematikai modellezési megközelítéshez [4] hasonlóan jó előrejelzésű modell építhető, és hogy a két modellből generált in-silico kísérlettervvel kapott eredmények egymással megegyező trendeket mutatnak.
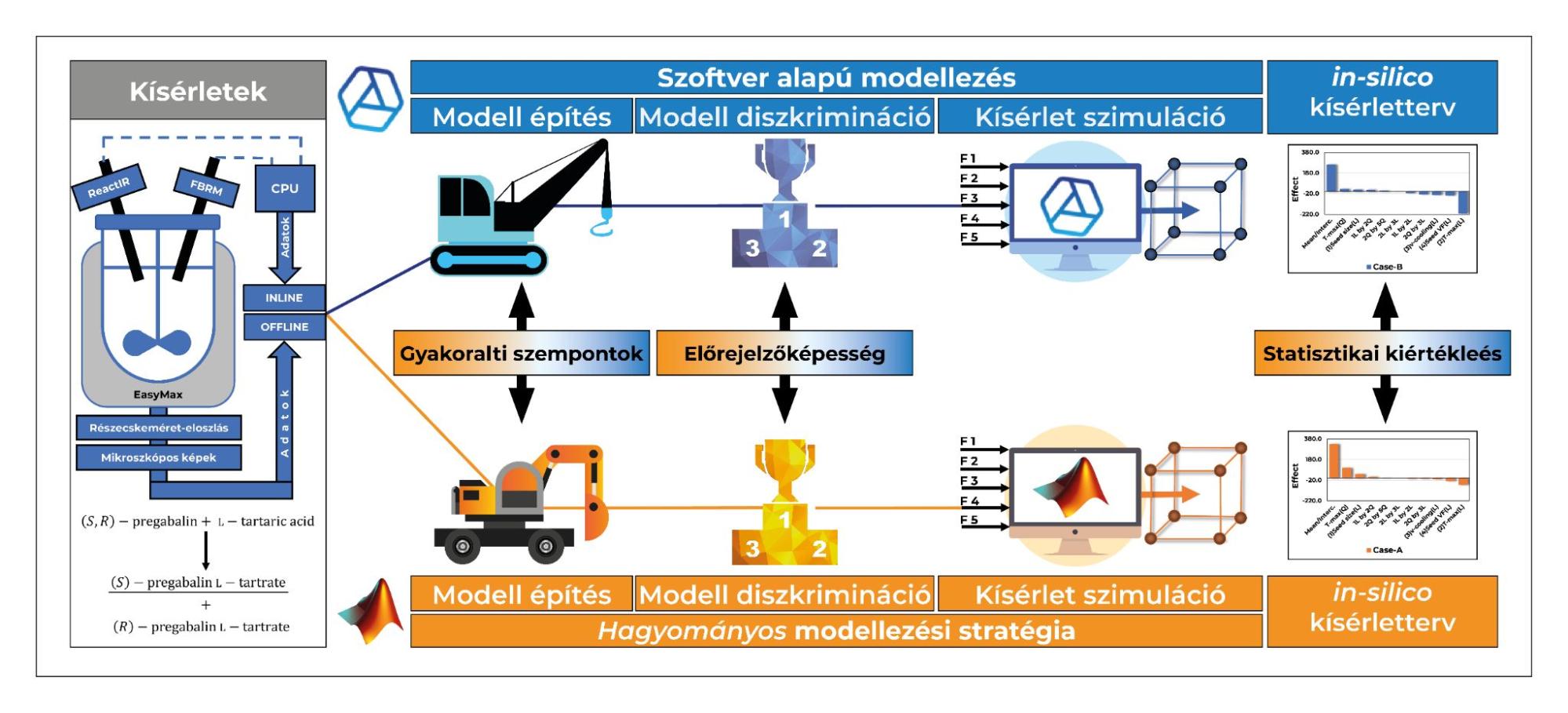
- ábra: A különböző PB modellezési megközelítéseket összehasonlító publikáció grafikus absztraktja [5]
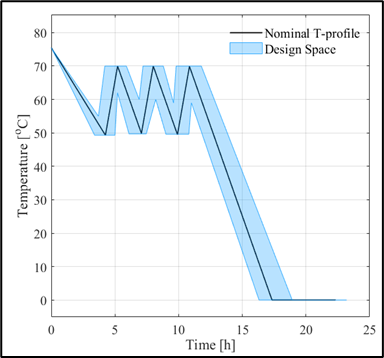
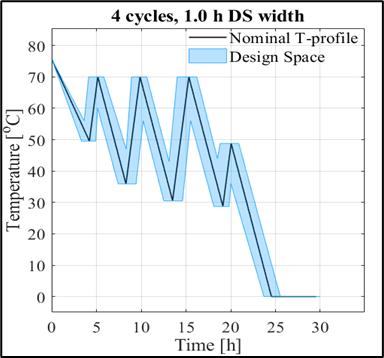
A munka további eredménye a módszerek magasabb szintű összehasonlítása volt: a hagyományos módszer bár lassabb, és több szaktudást igényel, de személyre szabható és rugalmasabb; a gyorsabb és kevesebb programozási ismeretet igénylő szoftveralapú modellezési módszernek viszont limitáltak a képességei. (2) A második témámban egy gyógyszerhatóanyag hűtéses kristályosításának modellezését, és a folyamat modellalapú optimalizációját végeztem el. A munka különlegessége, hogy többségében előre meglévő adatokból dolgoztam; kifejezetten ezekhez az eredményekhez kevés kísérlet elvégzésére volt szükség. A munka egyik eredményeként olyan modell született, mely egyszerre kezelhet kis- és nagyléptékű folyamatokat, így a laboros és üzemi folyamatoptimalizációt is. A folyamat optimalizálásakor a fő szempont a gyártási idő csökkentése és az energiaigény együttes minimalizálása volt. Az optimumot pedig nem egy nominális megoldásként fogalmaztuk meg, hanem egy tervezési térként (Design Space), melyen belül a megoldásunk érvényes marad.
|
|
|
|
|
|
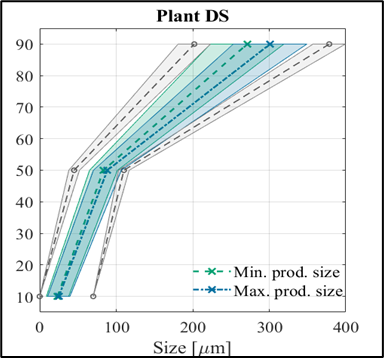
- ábra: A laboros (felül) és üzemi (alul) optimumok képei
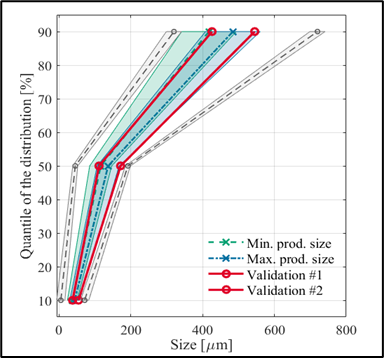
Az optimumok közül a laboros eredményeket validáló kísérletekkel teszteltük, és mint látható, a kapott kísérleti eredmények visszaigazolják a modell előrejelző képességét. Az üzemi hőmérsékletprofil-optimum külön érdekessége, hogy az általunk meghatározott sarzsidő hossza fele az üzemben jelenleg alkalmazottnak. (3) Harmadik témámban megvizsgáltam, hogy a keverési viszonyok hogyan képesek kézzelfogható módon előrejelezni a kristályosodás végtermékének jellemzőit. Ehhez 4 kisebb léptékű (0,5 L) hűtéses kristályosítási kísérletet végeztem el, az ezekhez kapcsolódó CFD-szimulációkat pedig a BME Hidrodinamikai rendszerek Tanszékének kutatói végezték el számunkra. Ezekből a szimulációkból megkaphattuk a keverési mezőt leíró fizikai jellemzők eloszlását. Azt vizsgáltam, hogy van-e kvantifikálható kapcsolat ezek és a termékméretek között. A modell illesztéséhez a PLSR-módszert használtam, majd egy nagyobb, 5 L léptékű külső validációs kísérletet végeztem, amellyel adekvát módon tesztelhettem a modell helyességét.
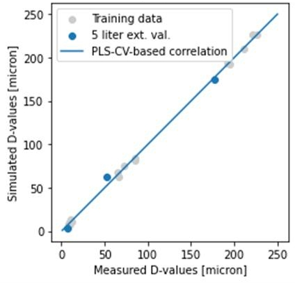
- ábra: Az illesztett modell és a validációs kísérlet egyezésének bemutatása
A 3. ábra mutatja a modell előrejelző képességét, és azt, hogy a keverési viszonyok megbízhatóan jelzik előre a várható termékméretet.
Várható impakt, további kutatás
A kutatásaim [4,5,6] várható impaktja a modellezési módszerek gyakorlati alkalmazásának növekedése, ezáltal kiszámíthatóbb, biztonságosabb folyamatok tervezése és működtetése a vegyiparban. További kutatásaimban a PB-módszerek fejlesztésére, adatelemzési módszerek alkalmazására kristályosítások előrejelzésében és modellezésében, valamint a keverési mezőből való pedikciós módszer más területeken (pl. szintézisek) való kipróbálására fogok koncentrálni.
Saját publikációk, hivatkozások, linkgyűjtemény
1. Chen J. et al. Cryst Growth Des. (2011), 887–895, 11(4)
2. Chung S.H. et al. Chemometrics and Intelligent Laboratory Systems. (2000), 83–90, 50
3. Nagy Z.K. et al. Chemical Engineering Research and Design. (2013),1903–1922, 91(10)
4. Bosits M.H., Orosz Á., et al. Cryst Growth Des. (2022),
5. Orosz Á. et al. Chemical Engineering Journal (2022), (submitted)
6. Orosz Á. et al. Front Chem. (2022), 10