George A. Olah Doctoral School of Chemistry and Chemical Technology 

Department of Chemical and Environmental Process Engineering

Supervisor: Dr. SZILÁGYI Botond

Development of digital tools for the design and synthesis of technological crystallization processes

Introducing the research area

The development of mathematical modeling methods related to crystallization, a technological process of great importance in the chemical industry, is the main focus of my research. I aim to develop these methods in a direction that can be immediately linked to answer practical questions in industry. My work can help to make pharmaceuticals, food products, fertilizers, and many other products safer, faster, and cheaper.

Brief introduction of the research place

My research is carried out in the newly established Crystallization and Process Engineering Research Group at the Budapest University of Technology and Economics. Our group is working on the control, deeper understanding, and optimization of crystallization and other chemical engineering processes using state-of-the-art computational tools. In this way, we are trying to bring together the disciplines of mathematics, chemistry, and computer science in an extremely exciting fusion, a multidisciplinary way of working that will bear practical fruit for industry.

History and context of the research

Crystallization is one of the most widely used chemical technologies, routinely used for separation and purification in industries ranging from pharmaceuticals to food and explosives. However, this long-established technology is of particular importance in the pharmaceutical industry, for example, where the process can improve the processability and bioavailability of the final product by orders of magnitude through precise process design. [1] The methods that have emerged in recent years and decades (population balance (PB) models, computational fluid dynamics (CFD), artificial intelligence (AI), and data analysis-based methods, etc.) can be of great help in the accurate and optimized design of these processes, making crystallization faster, more efficient and thus cheaper. [2,3] The above methods can be used to simulate experiments to replace physical experimentation, to find optimal production conditions more quickly, and to infer more reliably from process variables to take steps to improve our processes. In my Ph.D. topic, which is based on the above, I am looking for innovative applications of computing tools to deliver the products users need faster, in a more controlled way, and at lower cost. Through these, I can also help the industry get closer to the practical implementation of Industry 4.0 and Quality by Design (QbD) principles.

The research goals, open questions

In my research, I would like to apply modern mathematical modeling methods, which have already proven their applicability in other technical fields, to solve practical problems. I am also looking for new applications that can make the design, optimizations, or control processes of industrial manufacturing processes faster and cheaper. Thirdly, I am working on the development of tools that can be used in industry in an easy and practical way, thus minimizing the entry barrier that often hinders the industrial application of scientific innovations. In my research, I am looking for answers to the question: how can PB models be set up and then applied in practice more efficiently: using software or traditional methods? What can be done if we have little baseline data to set up the model? Beyond that, how can the properties of the mixing conditions be related to the effect of scale-up on crystal size?

Methods

The most widely used modeling method for crystallization processes is population balance (PB) modeling, which allows us to simulate the size, purity, and other properties of the product generated in our system, enabling us to plan, control, and optimize our processes faster and cheaper. The modeling method can be implemented in software (commercially available programs) or by traditional mathematical modeling (e.g., Matlab© or Python©). To build PB models, in addition to the size of the crystalline product and the solubility of the crystallizing compound, additional in-process data are needed, either on the concentration or on the number and size of crystals. In a real production process, however, these data are not always available in sufficient quantity or quality, which is a serious obstacle to the application of the method. To solve these problems, I have built three research topics in the PB modeling bundle: (1) modeling the same crystallization process in two separate ways: I perform a software (CrySiV) and a conventional one, and then compare the capabilities of the two modeling approaches in depth by generating in-silico experimental data with the two models and evaluating them; (2) I build a PB model for an industrial-scale crystallization process using mostly pre-existing data (thus staying close to the criterion of practicality) and perform a robust temperature-profile optimization with the mathematical model at industrial scale and laboratory scale. My third and last topic is to explore the relationship between (3) mixing conditions and the scale-up of crystallization processes using CFD simulations and PLSR (partial least squares regression) methods applied in mechanical engineering.

Results

(1) In the development of my first research topic, I was able to demonstrate, through modeling the cooling crystallization of pregabalin, that the CrySiV process simulation software can be used to build a good predictive model similar to the traditional mathematical modeling approach [4], and that the results obtained from the in-silico experimental design generated from the two models show consistent trends.

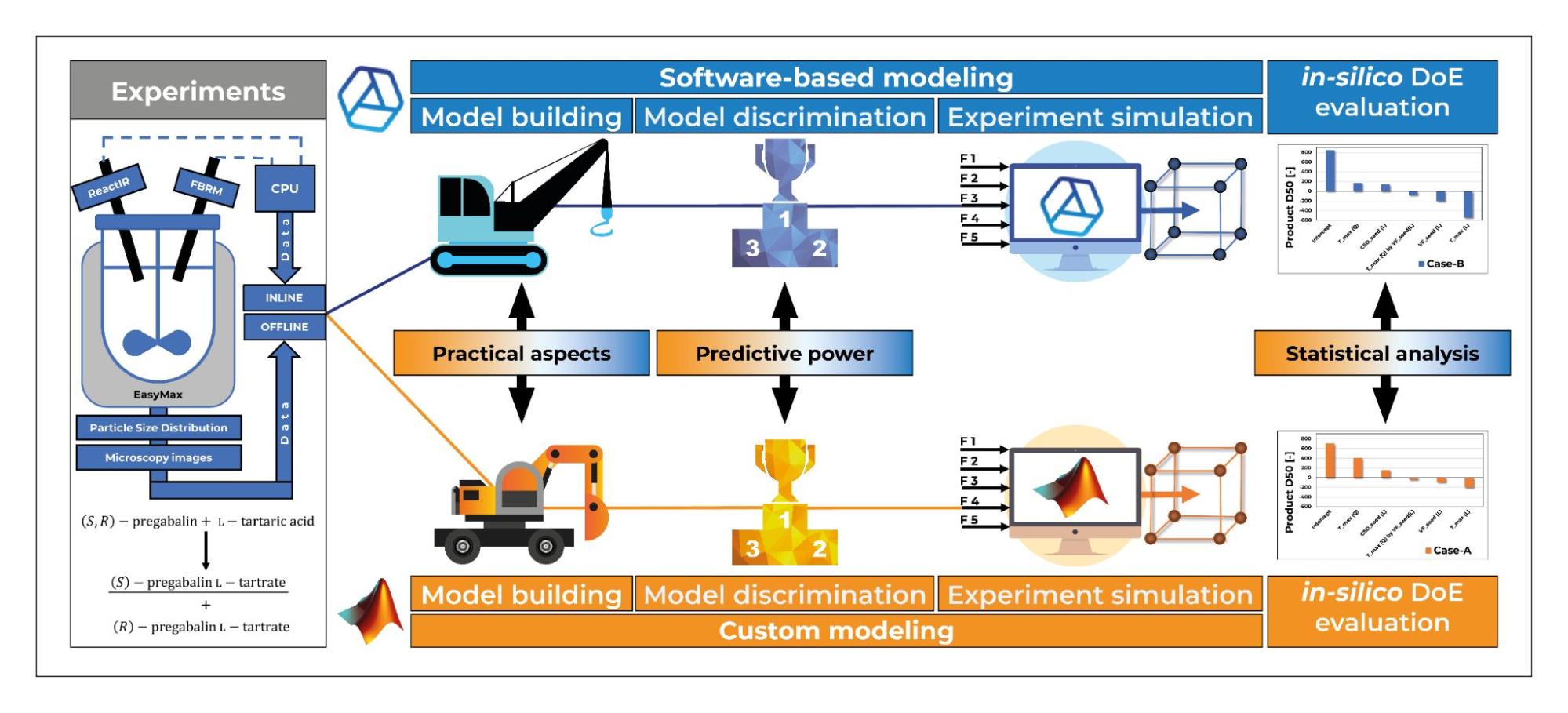
Figure 1: Graphical abstract of a publication comparing different PB modeling approaches [5].

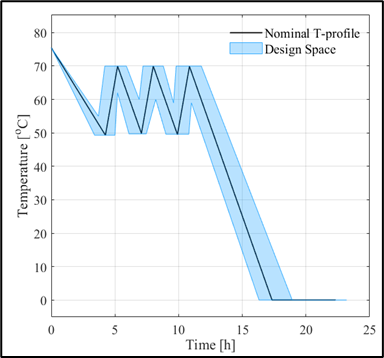
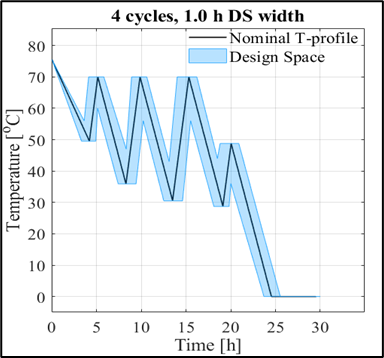
The work also resulted in a higher-level comparison of the methods: the traditional method, although slower and requiring more expertise, is more customizable and more flexible; whereas software-based modeling, which is faster and requires less programming knowledge, has limited capabilities (2). In my second topic, I carried out the modeling of the cooling crystallization of a drug substance and the model-based optimization of the process. The peculiarity of this work is that I worked mostly from pre-existing data, with only a few dedicated experiments to present to obtain results. One of the results of the work is a model that can handle both small- and large-scale processes so that both laboratory and shop floor process optimization can be performed with the model. The main focus of the process optimization was to reduce the production time and minimize the energy demand. The optimum was not formulated as a nominal solution, but as a Design Space within which our solution remains valid.

 

Figure 2: Images of the laboratory (top) and operational (bottom) optimum.

 

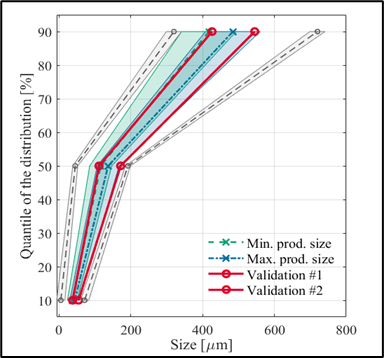
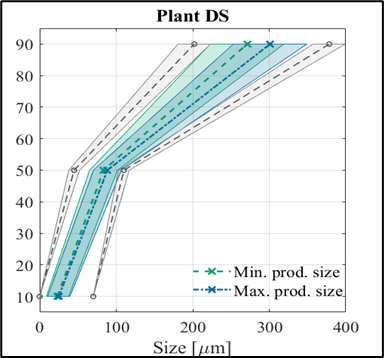
Among the optima, the laboratory results have been evaluated by validation experiments, and as can be seen, the experimental results obtained confirm the predictive capabilities of the model. A particularly interesting feature of the plant temperature profile optimum is that the length of the operating time we have identified is half of that currently used in the plant. (3) And in my third topic, I investigated how mixing conditions can predict the characteristics of the final crystallization product in a tangible way. For this purpose, I performed 4 small-scale (0.5 L) cooling crystallization experiments, and the associated CFD simulations were performed for us by researchers from the Department of Hydrodynamic Systems at BUTE. From these simulations, we obtained the distribution of the physical properties of the mixing field. I tried to find out if there is a quantifiable relationship between these and the product sizes. To fit the model, I used the PLSR method and validated it with an external validation experiment, a larger 5 L scale experiment to adequately assess the correctness of the model.

 

 

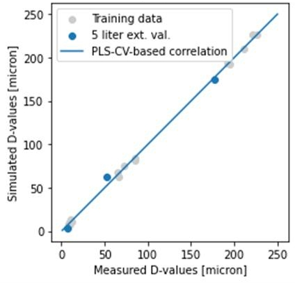
Figure 3: Illustration of the match between the fitted model and the validation experiment.

 

Figure 3 shows the predictive ability of the model and whether or not the mixing conditions reliably predict the expected product size.

Expected impact and further research

The expected impact of my research [4,5,6] is an increase in the practical application of modeling methods, leading to more predictable, safer process design and operation in the chemical industry. My future research will focus on the development of PB methods, the application of data analysis methods in the prediction and modeling of crystallization, and the testing of the prediction method from the mixing field in other fields (e.g., syntheses).

Publications, references, links

1.         Chen J. et al. Cryst Growth Des. (2011), 887-895,11(4)

2.         Chung S.H. et al. Chemometrics and Intelligent Laboratory Systems. (2000), 83–90,50

3.         Nagy Z.K. et al. Chemical Engineering Research and Design. (2013),1903–1922, 91(10)

4.         Bosits M.H., Orosz Á., et al. Cryst Growth Des. (2022),

5.         Orosz Á. et al. Chemical Engineering Journal (2022), (submitted)

6.         Orosz Á. et al. Front Chem. (2022), 10