Géza Pattantyús-Ábrahám Doctoral School of Mechanical Engineering 

BME GPK, Department of Energy Engineering

Suervisor: Dr. KOVÁCS Róbert Sándor

Non-Fourier heat conduction in everyday life

Introducing the research area

The heat pulse experiment is a well-known and widely used method for determining the thermal diffusivity of various materials. In recent years, it has been observed that the thermal behaviour of heterogeneous materials can deviate from the classical Fourier equation, resulting in different thermal diffusivity, and therefore additional thermal parameters are required for reliable evaluation.

 

Brief introduction of the research place

The Department of Energy Engineering has a long tradition of research on heat conduction, in which the work of László Kiss, Gyula Gróf and Tamás Környey has played an outstanding role. At present, the Irreversible Thermodynamics Research Group is involved in heat conduction research at the Department, and I am participating in the activities of this group.

 

History and context of the research

In various fields of engineering (such as thermodynamics, solid and fluid mechanics, and diffusion phenomena), a wide variety of models describing material behaviour are used, depending on the physical task at hand. In recent years, thermodynamics has started to play a prominent role in modelling material behaviour, allowing the range of existing models to be extended in a consistent way by means of a physically robust methodology.

 

In engineering applications, modern manufacturing technologies have led to the emergence of material structures that can no longer be described with the classical and well-known Fourier law with the desired accuracy.

 

In this research, metal foams obtained in collaboration with Imre Orbulov's research group are investigated and used for the development of a heat storage structure. Carbon foams are also investigated as part of the mechanical and thermal conduction systems of the CERN-ALICE next-generation detector. In addition, metal-organic framework samples for gas storage are available and are being investigated in collaboration with Krisztina László's research group.

 

The fundamental motivation for this research is to answer the question of how to thermally characterise materials with complex structures. For such characterisation, the heat pulse experiment is an established standard methodology. Fourier equation evaluation has long been known for the heat pulse experiment, but for heterogeneous materials, it does not describe the experimental data with sufficient accuracy, and the aim is to develop and extend it. Similar phenomena have been measured by NETZSCH independently of our research, making the continuation of this research even more meaningful.

 

The research goals, open questions

The aim and focus of the research are to investigate the applicability of generalised heat conduction models and their practical implementation. This will be achieved by analysing experiments available from the literature and by conducting experiments of our own, which will allow us to understand and thus design physical phenomena, such as the effect of heterogeneities on thermal conductivity, which are so far only superficially known.

 

In terms of modelling, two types of models can be distinguished. The first is where the material and its structural properties are known and exploited precisely, but this does not result in a universally applicable methodology. The other, which I use, is effective modelling and does not rely on knowing the exact material structure, so Fourier's law works, making the model more widely and effectively applicable.

 

The focus of my research is on the experiments and their evaluation. In addition to the Fourier equation, the evaluations also test several alternative heat conduction models and their practical feasibility. The aim is to formulate the range of applicability of the Fourier equation and to identify its limitations.

 

In the course of the research, I plan to investigate the aforementioned materials of practical relevance. There is also a need to improve the evaluation methodology of experiments with models other than Fourier. In addition, I plan to build another type of experiment in which the number of heat pulses and their length can be programmed, thus deepening our understanding of the phenomenon. The tools are at my disposal.

 

Methods

Using the heat pulse measurement method [1] (Figure 1), it is possible to determine the thermal diffusivity of the inserted sample at room temperature. The front surface of the inserted sample is excited by a heat pulse, in our case a flash lamp with a short pulse duration of 0.01 seconds. The effect of the pulse is measured on the rear side of the sample by a thermocouple which provides an electrical signal, and the data is digitised using a PC oscilloscope. Since the experimental setup is closed, the occurrence of a flash is indicated by a photovoltaic sensor located next to the sample holder. In all cases, the samples must be prepared before the experiment is performed (absorption, ensuring contacts). A consistent, uniform evaluation methodology using both Fourier and non-Fourier models is required for processing the experimental data [2].

 

 

Figure 1: Layout of the heat pulse experiment.

 

In the modelling, I consider several different heat conduction models. The first one in each case is the Fourier equation, but I also consider three alternative models. These models are the two-temperature model, the Guyer-Krumhansl equation [3] and the Jeffreys equation. In previous studies, I found that the two-temperature model has too many parameters to fit, the parameters of the fits are not straightforward, and so its use and further investigation were excluded. An iterative procedure based on sensitivity functions was developed for the evaluations. The Guyer-Krumhansl equation has been successfully applied to the samples, and the evaluation procedure still needs refinement and further testing. The applicability of the Jeffreys equation, together with its testing and evaluation methodology is being investigated.

 

For further testing and heat pulse experiments, a second lamp is also available, which is not capable of a single flash but can be programmed to deliver multiple heat pulses to the inserted sample. This allows testing the sensitivity of models and evaluation methodologies to the presence of multiple and different boundary conditions. The instrumentation background is already available to perform the experiments, with which I plan to re-run the experiments already performed with different settings allowed by the new lamp and instruments.

 

Results

In previous research on materials of various types and structures, I have found that the thermal diffusivity given by the Fourier equation cannot be reliably determined on a non-Fourier data set. By investigating alternative models for the Guyer-Krumhansl equation, a suitable and consistent evaluation method has been constructed, which can be applied to additional alternative models. I have developed an iterative procedure based on sensitivity function analysis, which is used to determine the unknown parameters of the model. By carrying out these evaluations, I have characterised seven types of rock, two types of carbon foams, five types of composite metal foams and two types of reduced graphene oxide materials.

 

Using the Guyer-Krumhansl equation, a relationship with the Fourier equation can be seen. The average of the time scales in the Guyer-Krumhansl equation provides the thermal conductivity given by the Fourier equation so that a simple relationship can be used to link the two models. From there, the heat conduction coefficient used in the Fourier equation can be derived from the alternative model. Thus, it can be said that the Fourier equation can be applied to non-Fourier materials, but only in a limited way. Such a relation is still unknown for the other alternative models. A significant result is that the Guyer-Krumhansl equation was equally applicable to different materials, thus providing a general model and approach to characterize materials.

 

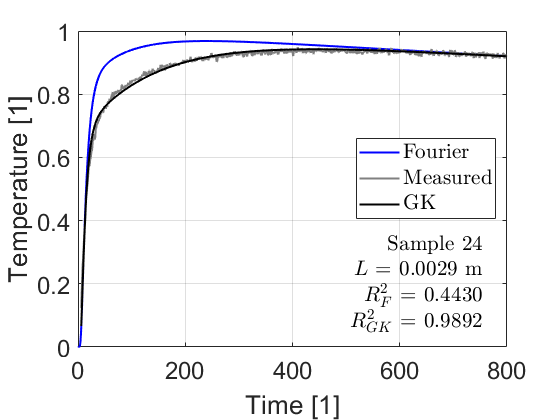
Figure 2: Evaluation of a metal foam sample using the Fourier equation and the Guyer-Krumhansl equation.

 

By general model we mean a model where the parameters in the model depend on the material structure, but where precise knowledge of the structure is not required but can be effectively taken into account for modelling purposes. Hence, thermal modelling of heterogeneous materials does not require accurate modelling of the structure and hence the use of supercomputers and extremely energy-intensive computational capacity. The long-term goal is to explore and design the relationship between the extra parameters of the extended heat conduction equation and the heterogeneous structure.

 

Expected impact and further research

As the research continues, further experiments will be conducted, and testing and putting into practice various alternative models are in process. The research and the methodology developed can answer the question of how to model complex structures with intricate material structures and how to incorporate them into a finite element environment by determining thermal parameters, which is expected to have a major impact on all areas of engineering practice. We foresee direct practical use of the existing designs in several areas of energy engineering (gas storage, thermal storage, efficiency improvement) as well as in the development of more precise measurement tools (CERN).

 

Publications, references, links

List of corresponding own publications:

 

Fehér A., Lukács N., Somlai L., Fodor T., Szücs M., Fülöp T., Ván P., Kovács R.: Size effects and beyond-fourier heat conduction in room-temperature experiments, JOURNAL OF NON-EQUILIBRIUM THERMODYNAMICS 46: 4 pp. 403–411, 9 p. (2021)

 

A. Fehér, R. Kovács.: On the evaluation of non-Fourier effects in heat pulse experiments, INTERNATIONAL JOURNAL OF ENGINEERING SCIENCE 169 Paper: 103577, 14 p. (2021)

 

R. Kovács, A. Fehér, S. Sobolev: On the two-temperature description of heterogeneous materials, International Journal of Heat and Mass Transfer, Volume 194, 2022, 123021, ISSN 0017-9310

 

Fehér Anna, Kovács Róbert: Heterogén anyagok hőimpulzus kísérletének kiértékelési eljárása, MAGYAR ENERGETIKA (1216-8599): 29:4 pp 2–10 (2022)

 

Anna Fehér; Róbert Kovács; Ákos Sudár; Gergely Barnaföldi: CHALLENGES IN THE THERMAL MODELING OF HIGHLY POROUS CARBON FOAMS, Journal of Thermal Analysis and Calorimetry, 2023, under review

 

Fehér Anna, Kovács Róbert: Általánosított termodinamikai modellek kísérleti kiértékelési módszertana, In: Takács, Donát M.; Ván, Péter; Vásárhelyi, Balázs (szerk.) Kőzetmechanika és termodinamika, Budapest, Hungary: Egyesület a Tudomány és Technológia Egységéért (2023) 189 p. pp. 3–16, 14 p.

 

Fehér A., Markovics D., Fodor T., Kovács R.: Size effects and non-Fourier thermal behaviour in rocks, In: Li, C.C.; Odegaard, H.; Hoien, A.H.; Macias, J. (Ed.) ISRM International Symposium - EUROCK 2020, Lisboa, Portugal: International Society for Rock Mechanics and Rock Engineering (2020) Paper: ISRM-EUROCK-2020-180, 7 p.

 

Anna Fehér, Róbert Kovács: Observing size effects in the thermal behaviour of rocks, 18TH INTERNATIONAL CONFERENCE OF YOUNG SCIENTISTS ON ENERGY AND NATURAL SCIENCES ISSUES, 2022

 

Anna Fehér, Róbert Kovács: Analytical evaluation of non-Fourier heat pulse experiments on room temperature, 4th IFAC Workshop on Thermodynamics Foundations of Mathematical Systems Theory TFMST 2022

 

Géczy, Attila; Csiszár, András; Xavier, Pascal; Corrao, Nicolas; Rauly, Dominique; Kovács, Róbert; Fehér, Anna Éva; Rozs, Egon; Gál, László: Thermal and RF Characterization of Novel PLA/Flax Based Biodegradable Printed Circuit Boards; 2022 IEEE 24th Electronics Packaging Technology Conference (EPTC)

 

 

List of references:

 

[1]    W. J. Parker, R. J. Jenkins, C. P. Butler, and G. É. Abbott. Flash method of determining thermal diffusivity, heat capacity, and thermal conductivity. Journal of Applied Physics, 32(9):1679-1684, 1961.

 

[2]    S. Both, B. Czél, T. Fülöp, Gy. Gróf, Á. Gyenis, R. Kovács, P. Ván and J. Verhás. Deviation from the Fourier law in room-temperature heat pulse experiments. Journal of Non-Equilibrium Thermodynamics, 41(1):41–48, 2016.

 

[3]        P. Ván, A. Berezovsky, T. Fülöp, Gy. Gróf, R. Kovács, Á. Lovas and J. Verhás. Guyer-Krumhansl-type heat conduction at room temperature. EPL, I118(5):50005, 2017. arXiv: 1704.00341v1.