Pattantyús-Ábrahám Géza Gépészeti Tudományok Doktori Iskola 

BME Gépészmérnöki Kar, Gép- és Terméktervezés Tanszék

Témavezető: Dr. Tamás Kornél, Dr. Bagi Katalin

Zúzottkő-halmazok numerikus modellezése

A kutatási téma néhány soros bemutatása

A szemcsés anyagok mechanikájának megértése, így a vasúti ágyazatoké is sok kihívást rejt. A teljes halmaz mechanikai viselkedését az azt felépítő alkotóelemek tulajdonságai (pl. anyag, méret, alak) és az elemek közti kapcsolatok jellemzői határozzák meg. Kutatásom fókuszában a vasúti ágyazatban található zúzottkő-szemcsék alakja áll, ami alapvetően befolyásolja az ágyazat teherbírását. Kísérleti úton laboratóriumi mérésekkel, és ezen mérések alapján kalibrált numerikus modellel keresem az optimális szemalakeloszlást. A létrehozott numerikus modell kiterjeszthető bármilyen, zúzottkövekből álló halmaz vizsgálatára, és alkalmas a zúzottkövekkel érintkező gépek virtuális tesztelésére is.

 

A kutatóhely rövid bemutatása

Az interdiszciplináris kutatást, amely gépész- és építőmérnöki tudományokat is érint, kettős témavezetés alatt végzem, és ipari partner is támogat. A téma befogadó intézménye a Gép- és Terméktervezés Tanszék, mely részéről Dr. Tamás Kornél egyetemi docens mentorál, építőmérnöki kérdésekben pedig Dr. Bagi Katalin egyetemi tanár, a Tartószerkezetek Mechanikája Tanszékről segíti a munkám. A két tanszék kapcsolata ezen a téren évtizedes múltra tekint vissza, jelenleg az NKFI OTKA K-138642 pályázat keretében működünk együtt.

A kutatás szoftveres hátterét az Itasca Consulting Group és az Itasca Consultants SAS támogatja az IEP Research Program keretében, melyben a mentorom Dr. Fabian Dedecker főmérnök. A laboratóriumi vizsgálatok a Széchenyi István Egyetem Szerkezetvizsgáló Laboratóriumában zajlottak.

 

A kutatás történetének, tágabb kontextusának bemutatása

A vasút jelentős szerepe a teher- és személyszállításban vitathatatlan. Bár a sínek alátámasztására több megoldás is létezik, a mai napig a legelterjedtebb és leggazdaságosabb a hagyományos megoldás, ahol a sínek és az őket tartó keresztaljak zúzottkő-ágyazaton fekszenek. A vasúti ágyazatra vonatkozó EN 13450 [1] szabvány részletesen szabályozza a kövek méretének eloszlását, azonban kisebb hangsúlyt fektet azok alakjára. A lapos alakú lemezes szemcsék jelenléte a halmazban növeli annak nyírószilárdságát a kiékelődés miatt [2, S4, S8], azonban ezek könnyeben is törnek, mint a gömbhöz közelebb álló zömök kövek [3]. Ez arra enged következtetni, hogy létezik a lemezes és zömök köveknek egy optimális aránya.

Az iparban általános törekvés, hogy a költséges és időigényes kísérleti vizsgálatokat minél nagyobb mértékben szimulációkkal váltsuk ki. A jól kalibrált és validált numerikus modellekkel sok esetben olyan információkhoz juthatunk, amelyeket kísérletileg nem tudnánk feltárni. A kontinuumként modellezhető anyagok szimulációja az ipari gyakorlatban mindennaposnak számít, a szemcsés anyagok modellezése azonban sokkal összetettebb, és kontinuumként való modellezésük gyakran nem is lehetséges. Ilyen problémát jelent például, ha a szemcsék elmozdulása nagy, vagy ha a halmaz átrendeződésének mechanikai hatása van, illetve, ha a szemcsék különböző tulajdonságainak a teljes halmaz mechanikai viselkedésre gyakorolt hatásaira vagyunk kíváncsiak. Ez esetben a szemcséket egymástól különálló testekként kell kezelnünk, és részecskealapú szimulációs módszereket kell alkalmaznunk.

 

A kutatás célja, a megválaszolandó kérdések

A kutatás első, építőmérnöki vonatkozású célja, hogy megtalálja a vasúti zúzottkő-halmazokban a lemezes és zömök szemcsék azon optimális arányát, mellyel a halmaz a statikus nyírásnak legjobban ellenáll. A második cél egy olyan numerikus modell létrehozása, amely segítséget nyújt a gépészmérnököknek zúzottköveket kezelő gépek optimalizálásában.

 

Módszerek

Szemcsés anyagok szimulációjára kiváló a diszkrételemes módszer (DEM) [4], ezért ezt alkalmaztam [S3, S12, S14]. A zúzottköveket poliéder alakú elemekkel reprezentáltam. A szemalak számszerűsítésére számos mutatószám létezik, de egyetértés nincs abban, melyik(ek) a legjobb(ak). A hagyományos mutatószámokon túlmenően speciális súlyozott váztenzorokat [5] is alkalmaztam, amelyek közvetlenül a digitalizált geometria felületi (3D szkennelés), vagy térfogati (CT) reprezentációjára építenek. A digitalizált geometriából kiszámolt tenzorok – felületirányítottsági [S6] és térfogateloszlási tenzor – sajátértékeiből kalkulálható a szemcse zömökségi, lemezességi és hosszúkássági mértéke, míg a tenzor sajátvektorai a szemcse karakterisztikus irányait adják meg. A mutatószámok kiszámolásához a SHAPE [6] nevű, Matlab-alapú könyvtárat használtam.

100 darab zúzottkövet (50 zömök, 50 lemezes) szkenneltem DAVID SLS-3 strukturált fényszkennerrel. A szkennelés eredményeként kapott adathalmazt további műveleteknek kellett alávetnem a szimulálhatósághoz, pl. a virtuális köveket egyszerűsítettem (1. ábra). A célra saját Matlab- és Python-alapú algoritmusokat dolgoztam ki, a PyMeshLab [7] és SHAPE könyvtárakra építve.

 

1. ábra. A kődigitalizálás és egyszerűsítés folyamata

 

Kiválasztottam a lehetséges kapcsolati modelleket (és szoftvereket, amelyek ezeket tartalmazzák): Eliáš-modell [8] (Yade [9]), GJK+EPA (PFC [10]) és sub-contact (3DEC [11]), amelyeket különböző alapvető mechanikai problémák modellezésével hasonlítottam össze.

A DEM modell mikromechanikai és a halmaz kísérletekben mérhető makromechanikai paraméterei között nem létezik analitikus összefüggés, így a DEM-modellt valós mérésekhez kell kalibrálni [S11]. A csúszási súrlódási paraméterek becsléséhez egyszerű direkt méréseket hajtottam végre, a halmaz makromechanikai tulajdonságainak mérésére pedig nagyméretű nyíródobozos berendezést (2. ábra) alkalmaztam. Háromféle halmazt mértem: egy zömök, egy lemezes szemcséket tartalmazót, és egy vegyes halmazt. A mérési eredmények már önmagukban is szolgáltattak eredményeket, de lemezes és zömök szemcsék optimális arányát a szimulációk fogják pontosan megadni.

 

2. ábra. Nagyméretű nyíródobozos berendezés (balra) és numerikus modellje (jobbra)

 

A szemcsék törését is modellezem: amikor az adott szemcsében ébredő átlagos feszültség meghaladja a törési feltételt, a szemcsét egy vagy két sík darabolja fel. Többféle már meglévő törésmodellt beprogramoztam a PFC-be, és újakat is definiáltam.

A gépekben ébredő feszültségek számolására a végeselemes módszer (VEM) gyakran alkalmazott. A szemcsékkel érintkező szerszámok felületén ébredő erők megoszlása összetett, így a modell pontatlanabb lesz, ha ezeket egy homogén megoszló erővel helyettesítjük. A felületi erők eloszlásának meghatározása viszont elvégezhető a DEM módszerrel. Ezért egyirányú kapcsolatot hoztam létre a Yade és ANSYS [S10, S13], valamint PFC és ANSYS közt.

 

Eddigi eredmények

Bebizonyítottam, hogy a szemalak számszerűsítésére és a szemcsék karakterisztikus irányainak meghatározására a felületirányítottsági és a térfogateloszlási tenzor több tekintetben előnyösebb a legkisebb körülírható téglatest alapú módszereknél [S1]: a geometria egyszerűsítésére kevésbé érzékenyek, és az éles, kiálló sarkok sincsenek nagy hatással az alakot leíró mérőszámokra. A 100 szkennelt szemcse elemzésével feltártam a szabványos, manuális (EN 933-3 [12], EN 933-4 [13]), és a digitális képalkotásra épülő leggyakoribb szemalak-meghatározó módszerek közti összefüggéseket.

A nagyméretű nyíródobozos mérések összesített eredménye igazolta a sejtést, ami szerint a nyírással szemben a vegyes halmaz a legellenállóbb, mivel a vegyes halmaz tönkremeneteli egyenesének a legnagyobb a meredeksége (3. ábra, bal oldal).

Bebizonyítottam, hogy a Yade, PFC és 3DEC szoftverekben található poliéderes modellek közül a PFC-be beépített GJK+EPA modell a legjobban alkalmazható szemcsés anyagok szimulációjára, így más kutatóknak már nem kell a többi szoftvert tesztelnie.

Létrehoztam a mérés diszkrételemes modelljét. A 3. ábra jobb oldala egy tipikus feszültség-elmozdulás diagramot mutat egy mérés és a hozzá tartozó numerikus modell esetén. A modell a nyírás kezdeti szakaszában nagyon jól közelíti a kísérleteket, de a tönkremenetel után a nyíróerő a modellben visszaesik, így a modell további kalibrálásra szorul. Fontos azonban megjegyezni, hogy a bemutatott eredmények még csak a második paraméterkombinációval futottak le, amit figyelembe véve a modell eredményei biztatóak.

 

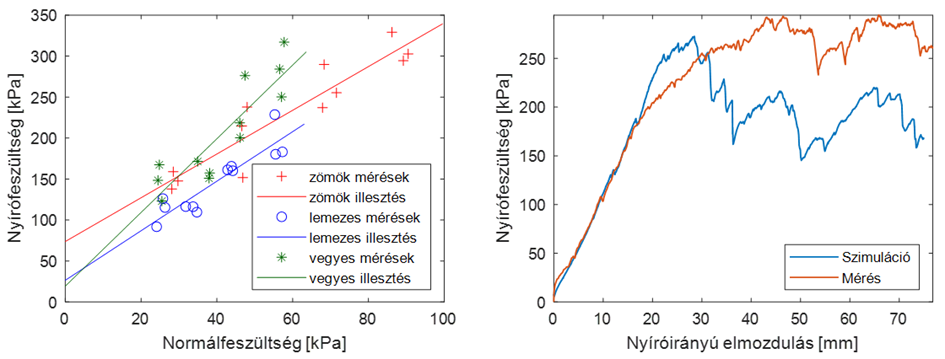
3. ábra, bal oldal: különböző halmazok tönkremeneteli diagramjai, jobb oldal: szimuláció és mérés eredményeinek összevetése nyírófeszültség [kPa] – nyíróirányú elmozdulás [mm] diagramon egy tipikus esetben (zömök halmaz, 80 kPa névleges normálfeszültség)

 

Az irodalomban megtalálható, illetve az általam létrehozott törésmodelleket egy darab szemcse alapvető terhelési eseteit (egytengelyű nyomás, nyírás, hárompontos hajlítás, hasítás) modellező szimulációkkal vizsgáltam. A 4. ábra bal oldala mutatja az Eliáš-féle modellt [8], míg a jobb oldala egy új jelöltet, egytengelyű nyomás által okozott törés esetén. Mindegyik modell jól teljesített bizonyos terhelési esetekben, de valamennyit egyik se tudta egyszerre lemodellezni. Ennek az az oka, hogy az alkalmazott kapcsolatkezelési modell túl egyszerű, és nem tartalmaz minden információt, pl. csak egy átlagolt feszültséget számol a szemcsékre. A jövőben ezért megvizsgálom, melyik terhelés a leggyakoribb a halmazokban, és a törésmodellek azon kombinációját alkalmazom, amelyek a legjobban tudják a tönkremenetelt ebben a terheléstípusban modellezni.

A létrehozott egyirányú kapcsolatot diszkrételemes szoftverek (Yade és PFC), valamint a végeselemes ANSYS közt több alkalmazási feladatban [S7, S9] sikerrel teszteltem.

 

4. ábra. Egyedi szemcsék törése szimulációkban egytengelyű nyomás hatására. Bal oldal: Eliáš-modell, jobb oldal: egy új, lehetséges modell

 

Várható impakt, további kutatás

A szemalak-elemzés terén jelen kutatás így egy teljesen új, meglévő módszerekhez képest előnyökkel bíró módszercsoportot ad a kutatók kezébe. Feltártam különböző szemalak-leíró módszerek közti összefüggéseket is, így a különböző eljárásmódokat alkalmazó kutatások is összehasonlíthatóak lesznek.

Már az eddigi kísérletek is bebizonyították, hogy a lemezes és zömök szemcséket is tartalmazó halmazok a legerősebbek, amit érdemes minden zúzottkő-halmaz készítésénél, és szabványok létrehozásánál is figyelembe venni. A továbbiakban a létrehozott szimulációs modellt kalibrálom, majd megállapítom vele az optimális szemalak-arányt, illetve a törés hatását is vizsgálni fogom.

A kidolgozott egyirányú véges-diszkrételemes kapcsolt szimuláció eszközt ad a mérnökök kezébe a zúzottkövekkel érintkező gépek virtuális teszteléshez.

A megfelelő alakú szemcsék kiválogatása a kísérletekhez igen hosszadalmas folyamat, ezért megvizsgáltuk, hogyan lehet hasonló mechanikai viselkedésű szemcséket gyártani [S2]. A jövőben ezekkel végzünk majd további kísérleteket.

 

Saját publikációk, hivatkozások, linkgyűjtemény

Kapcsolódó saját publikációk listája.

[S1] Orosz Á, Angelidakis V, Bagi K. Surface orientation tensor to predict preferred contact orientation and characterise the form of individual particles, Powder Technol. 394 2021, p. 312–325. https://doi.org/10.1016/j.powtec.2021.08.054. (IF 5,134)

[S2] Szabó B, Pásthy L, Orosz Á, Tamás K. The investigation of additive manufacturing and moldable materials to produce railway ballast grain analogs, Frat. Ed Integrità Strutt. 16 2022, p. 213–228. https://doi.org/10.3221/IGF-ESIS.60.15. (Q2)

[S3] Orosz Á, Tamás K, Rádics J.P. The feasibility of modelling rocks in engineering applications with the use of discrete element method, Hung. Agric. Eng. 2017, p. 51–55. https://doi.org/10.17676/HAE.2017.32.51.

[S4] Gálos M, Orosz Á. Ágyazati kőanyagok viselkedésének vizsgálata ismételt terhelés hatására. Sínek Világa 61 2019, p. 10–15.

[S5] Gálos M, Orosz Á, Rádics JP, Tamas K. Diszkrét elemes számítógépes módszer a vasúti zúzottkő ágyazat viselkedésének modellezésére. Sínek Világa 59, 2017, p.22–28.

[S6] Bagi K, Orosz A. A New Variable for Characterising Irregular Element Geometries In Experiments And DEM Simulations. ECMS 2020 Proc. Ed. Mike Steglich Christ. Mueller Gaby Neumann Mathias Walther, ECMS; 2020, p. 256–260. https://doi.org/10.7148/2020-0256.

[S7] Orosz A, Zwierczyk PT. Analysis of the Stress State of a Railway Sleeper Using Coupled FEM-DEM Simulation. ECMS 2020 Proc. Ed. Mike Steglich Christ. Mueller Gaby Neumann Mathias Walther, ECMS; 2020, p. 261–265. https://doi.org/10.7148/2020-0261.

[S8] Orosz A, Tamas K, Radics JP, Galos M. Studying the Behaviour of Crushed Stone Railway Ballast Subjected to Periodic Load. ECMS 2019 Proc. Ed. Mauro Iacono Francesco Palmieri Marco Gribaudo Massimo Ficco, ECMS; 2019, p. 384–388. https://doi.org/10.7148/2019-0384.

[S9] Vajda M.Zs, Olah Z, Orosz A. Evaluating the Stress Field on Sweep During Tillage Process Applying Coupled Finite-Discrete Element Method. ECMS 2019 Proc. Ed. Mauro Iacono Francesco Palmieri Marco Gribaudo Massimo Ficco, ECMS; 2019, p. 358–363. https://doi.org/10.7148/2019-0358.

[S10]           Orosz A, Tamas K, Radics JP, Zwierczyk PT. Coupling Finite and Discrete Element Methods Using an Open Source and a Commercial Software. ECMS 2018 Proc. Ed. Lars Nolle Alexandra Burger Christoph Tholen Jens Werner Jens Wellhausen, ECMS; 2018, p. 399–404. https://doi.org/10.7148/2018-0399.

[S11]           Orosz A, Radics JP, Tamas K. Calibration of railway ballast DEM model. Proc. 31st Eur. Conf. Model. Simul., Budapest: European Council for Modeling and Simulation; 2017, p. 523–528. https://doi.org/10.7148/2017-0523.

[S12]           Gálos M, Orosz Á, Rádics JP, Tamás K. Modelling the behaviour of concrete additives via discrete element numerical simulation. Innov. Mater. Technol. Concr. Struct. Proc. Fib Congr., Tokaj: Hungarian Group of fib; 2017, p. 607–614.

[S13]           Orosz Á, Zwierczyk PT, Rádics JP, Tamas K. A véges és a diszkrét elemes szimulációk kapcsolásának jelentősége a géptervezésben, Marosvásárhely, Románia: Erdélyi Magyar Műszaki Tudományos Társaság (EMT); 2018, p. 333-336.

[S14]           Orosz Á, Rádics JP, Tamás K. Zúzottkő diszkrét elemes modelljének létrehozása vasúti pályakarbantartó gépek fejlesztéséhez. OGÉT 2017 XXV Nk. Gép. Konf. 25th Int. Conf. Mech. Eng., Kolozsvár: Erdélyi Magyar Műszaki Tudományos Társaság (EMT); 2017, p. 291–294.

 

 

Linkgyűjtemény.

Gép- és Terméktervezés Tanszék honlapja

Tartószerkezetek Mechanikája Tanszék honlapja

Itasca Consulting Group honlapja

Itasca Consultants SAS (Itasca France) honlapja

Itasca Educational Partnership Research Program

 

Hivatkozások listája.

[1]    EN 13450, Aggregates for railway ballast 2002.

[2]    Liu Y, Gao R, Chen J. Exploring the influence of sphericity on the mechanical behaviors of ballast particles subjected to direct shear. Granul Matter 21 2019, 94. https://doi.org/10.1007/s10035-019-0943-1.

[3]    Zhang T, Zhang C, Zou J, Wang B, Song F, Yang W. DEM exploration of the effect of particle shape on particle breakage in granular assemblies. Comput Geotech 122 2020. 103542. https://doi.org/10.1016/j.compgeo.2020.103542.

[4]    Cundall PA, Strack ODL. A discrete numerical model for granular assemblies. Géotechnique 29 1979. p. 47–65. https://doi.org/10.1680/geot.1979.29.1.47.

[5]    Satake M. Fabric tensor in granular materials. In: Luger VA, editor. Deform. Fail. Granul. Mater., Delft, Netherlands: A. A. Balkema, Rotterdam, Ne; 1982. p. 63–68.

[6]    Angelidakis V, Nadimi S, Utili S. Shape Analyser for Particle Engineering (SHAPE): Seamless characterisation and simplification of particle morphology from imaging data. Comput Phys Commun 265 2021. 107983. https://doi.org/10.1016/j.cpc.2021.107983.

[7]    Cignoni P, Callieri M, Corsini M, Dellepiane M, Ganovelli F, Ranzuglia G. MeshLab: an Open-Source Mesh Processing Tool. In: Scarano V, Chiara RD, Erra U, editors. Eurographics Ital. Chapter Conf., The Eurographics Association; 2008. https://doi.org/10.2312/LocalChapterEvents/ItalChap/ItalianChapConf2008/129–136.

[8]    Eliáš J. Simulation of railway ballast using crushable polyhedral particles. Powder Technol 264 2014. p. 458–465. https://doi.org/10.1016/j.powtec.2014.05.052.

[9]    Šmilauer V, Catalano E, Chareyre B, Sergei D, Duriez J, Gladky A, et al. Yade Documentation. 2nd ed. The Yade Project; 2016.

[10]  PFC - Itasca’s Particle Flow Code Documentation. Minneapolis, USA: Itasca Consulting Group, Inc.; 2018.

[11]  3DEC - 3-Dimensional Distinct Element Code, Online Manual. Minneapolis, USA: Itasca Consulting Group, Inc.; 2016.

[12]  EN 933-3:2012, Tests for geometrical properties of aggregates. Part 3: Determination of particle shape. Flakiness index, Standard 2012.

[13]  EN 933-4:2008, Tests for geometrical properties of aggregates. Part 4: Determination of particle shape. Shape index, Standard 2008.