Pattantyús Ábrahám Géza Doctoral School of Mechanical Engineering 

BME Faculty of Mechanical Engineering, Department of Machine and Product Design

Supervisors: Dr. Tamás Kornél, Dr. Bagi Katalin

Numerical modeling of crushed rock aggregates

Introducing the research area

Understanding the mechanical behavior of granular materials such as railway ballast poses many challenges. The mechanical behavior of the entire assembly is governed by the properties (e.g. material, size, shape) of the particles that make it up and the properties of their contacts. The research focuses on the shape of crushed rock railway ballast grains which has a great impact on the strength of the railway ballast. The optimal shape distribution is sought with laboratory experiments and numerical models which have been calibrated based on these experiments. The established numerical model can be applied to model any crushed rock aggregate and is suitable to test machines that interact with crushed rock aggregates.

 

Brief introduction of the research place

This interdisciplinary research, related to both mechanical and civil engineering sciences is, carried out under dual supervision and is also supported by an industrial partner. The host institute for the topic is the Department of Machine and Product Design, where my mentor is Dr. Kornél Tamás, I am supported by Dr. Katalin Bagi from the Department of Structural Mechanics in civil engineering matters. The relationship between the two institutions dates back more than a decade. Currently, we are working together in the framework of the NKFI OTKA K-138642 grant.

The software background of the research is supported by Itasca Consulting Group and Itasca Consultants SAS within the framework of the IEP Research Program, where my mentor is Dr. Fabian Dedecker principal engineer. The laboratory tests were conducted at the Structure Investigation Laboratory of Széchenyi István University.

 

History and context of the research

The significant role of railways in cargo and passenger transport is unarguable. Although there are multiple solutions to support the rails, the most widespread and economical solution is the traditional one, when the rails and the sleepers are laid on crushed rock aggregate. The EN 13450 [1] railway ballast standard specifies the size distribution of the stones but does not give so much attention to their shape. The existence of flat grains in the aggregate increases its shear strength due to interlocking [2, S4, S8], but on the other hand, these stones are more prone to breakage [3] than the compact ones, whose shape is closer to a sphere. This leads to the conclusion that there is an optimal ratio of flat and compact grains.

Nowadays, the general trend in the industry is to replace the cost and time-demanding experimental investigations with simulations as much as possible. Properly calibrated and validated numerical models often provide us extra with additional information, which is impossible to obtain through experiments. The simulation of materials that can be modeled as a continuum has become an industrial practice, however, the modeling of granular materials is much more complex. Particulate materials cannot be modeled as a continuum in many cases, e.g. where the displacements of the grains are large, the realignment of the assembly has a mechanical effect, or when the effect of the grain properties on the mechanical behavior of the assembly is investigated. In these cases, the grains have to be modeled as discrete bodies, which poses the need for particle-based simulation methods.

 

The research goals, open questions

The first, civil engineering-related aim of the research is to find the optimal ratio of flat and compact grains, which gives the assembly the highest shear strength. The second aim is to create a numerical model that helps mechanical engineers optimize machines that interact with rock aggregates.

 

Methods

The discrete element method (DEM) [4] is excellent to model granular materials, therefore this technique was applied [S3, S12, S14]. Crushed stones were represented by polyhedral elements. There are several shape indices to quantify shape, but there is no consensus as to which is/are the most suitable. Besides traditional indices, special weighted fabric tensors [5] were applied, which are based directly on digitized geometry, which can be a surface (3D scanning) or a volumetric (CT) representation. From the eigenvalues of computed tensors – the surface orientation and the volume distribution tensor – the compactness, flakiness, and elongation of the grain can be calculated, while its eigenvectors define the characteristic orientations. The open-source, Matlab-based software SHAPE [6] was used to compute the shape indices.

100 grains (50 compact, 50 flat) have been scanned with a DAVID SLS-3 structured light scanner. The resulting data had to be processed for use in simulations, e.g. the virtual grains had to be simplified (Figure 1). New Matlab and Python algorithms were written for this purpose, relying on PyMeshlab [7] and SHAPE libraries.

 

Figure 1. The steps of stone digitization and simplification

 

Three candidate models (and software into which they are implemented) were chosen: Eliáš-model [8] (Yade [9]), GJK+EPA (PFC [10]), and sub-contact (3DEC [11]). They were compared based on their performance in modeling fundamental mechanical problems.

There is no analytical expression between the micromechanical properties of the DEM model and the experimental macromechanical parameters of the assembly, therefore the DEM model has to be calibrated based on experiments [S11]. Direct measurements were carried out to estimate the friction parameters, and large-scale direct shear box tests (Figure 2.) were conducted to measure the macromechanical properties of the assembly. Three types of aggregates were tested: compact, flat, and mixed. The experiments have already provided valuable results, but the exact optimal ratio of flat and compacted grains will be determined based on the simulations.

 

Figure 2. Large-scale direct shear box apparatus (left) and its numerical model (right).

 

The breakage of the grains was modeled as well: when the averaged stress exceeds the failure criterion, the grain is cut by one or two planes. Multiple existing models were implemented into PFC and new ones were defined as well.

The finite element method (FEM) is often used to calculate the stresses arising in machines. The force distribution on the surface of the tools that are in interaction with granular materials is complex, therefore the model is less accurate if it is substituted with a homogeneously distributed force. However, the force distribution can be computed with DEM simulations. Therefore, a one-way coupling was established between Yade and ANSYS [S10, S13] as well as between PFC and ANSYS.

 

Results

It was proved that the surface orientation and the volume distribution tensors perform better in quantifying shape and computing the characteristic orientations than traditional oriented bounding box-based methods [S1]: they are less sensitive to the simplification of the geometry, and the sharp corners have no significant effect on the shape indices. The relationships between the standard manual methods (EN 933-3 [12], EN 933-4 [13]) and the most frequent digital imaging-based approaches were also revealed in studying the 100 scanned grains.

The large-scale shear box experiments confirmed the expectation that the mixed assembly has the highest shear resistance because this type of aggregate had the biggest internal friction angle (Figure 3, left).

It has been proven that of the polyhedral models implemented into Yade, PFC, and 3DEC, the GJK+EPA model built in PFC is the most suitable to simulate bulk materials, so other researchers do not have to investigate other software.

The discrete element models of the experiments were created. The right side of Figure 3 shows a typical stress-displacement diagram of an experiment and its corresponding simulation. The model matches the experiment well at the initial phase of the shear process; however, the shear force drops after the failure of the assembly, therefore the model requires further calibration. However, it is important to note that the presented results are only for the second iteration of parameter values. Taking this into consideration, the results of the model are promising.

 

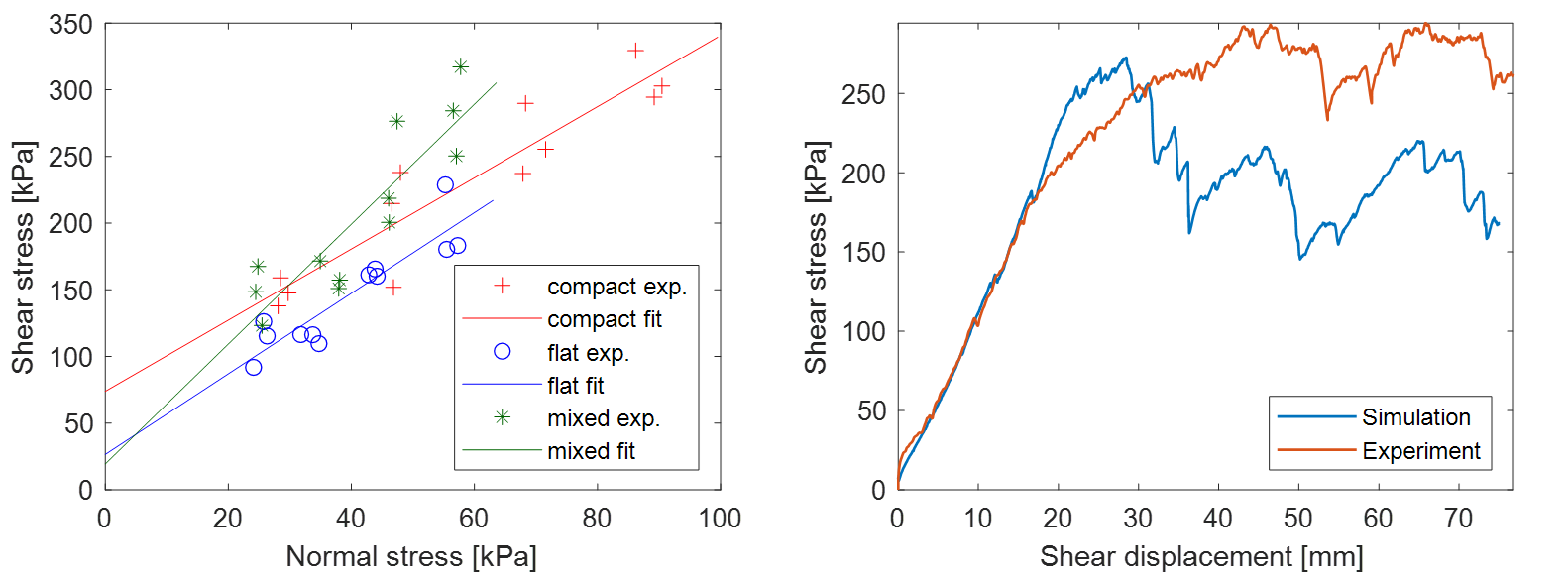
Figure 3. Left: the yield lines of the different aggregates, right: comparison of numerical and experimental results on the shear stress [kPa] – shear displacement [mm] diagram in a typical case (compact aggregate, 80 kPa nominal normal stress).

 

Breakage models from the literature and new candidates were compared based on their performance in modeling fundamental load cases (uniaxial compression, shear, three-point bending, splitting). The left side of Figure 4 shows the Eliáš breakage model [8], while the right side shows a new candidate in the case of a failure caused by uniaxial compression. All models performed well in certain load cases, but none could simulate all of them. The reason is that the applied contact treatment method is too simple and does not contain all the necessary information, e.g. only an averaged stress is computed for the grains. It will be investigated which load case is the most frequent and a combination of breakage models will be applied that best models that load case.

The created one-way connection between the discrete element software (Yade and PFC), and finite element ANSYS was successfully tested in multiple applications [S7, S9].

Figure 4. Breakage of single grains due to uniaxial compression. Left side: Eliáš-model, right side: a new candidate model.

 

Expected impact and further research

The results of the research on shape characterization offer researchers novel methods that have advantages over the existing methods. The relationships between different shape characterization methods were also revealed, therefore investigations using different approaches will be comparable.

The experimental results revealed that those aggregates have the highest shear strength which consists of both flat and compact grains. This is advised to be considered during the manufacturing of assemblies and the creation of standards. In the further steps of the research, the simulation model will be properly calibrated and used to determine the optimal flat-to-compact ratio and to study the effect of breakage.

The established one-way discrete-finite element coupled simulation offers engineers a tool for virtual testing of the machines that interact with crushed rock aggregates.

Selecting suitable ballast grains for experiments is a tedious process, therefore possible methods for producing grain analogs were investigated [S2]. Further experimental investigations will be carried out with these artificial grains in the future.

Publications, references, links

List of corresponding own publications.

[S1] Orosz Á, Angelidakis V, Bagi K. Surface orientation tensor to predict preferred contact orientation and characterize the form of individual particles, Powder Technol. 394 2021, p. 312–325. https://doi.org/10.1016/j.powtec.2021.08.054. (IF 5.134)

[S2] Szabó B, Pásthy L, Orosz Á, Tamás K. The investigation of additive manufacturing and moldable materials to produce railway ballast grain analogs, Frat. Ed Integrità Strutt. 16 2022, p. 213–228. https://doi.org/10.3221/IGF-ESIS.60.15. (Q2)

[S3] Orosz Á, Tamás K, Rádics J.P. The feasibility of modeling rocks in engineering applications with the use of discrete element method, Hung. Agric. Eng. 2017, p. 51–55. https://doi.org/10.17676/HAE.2017.32.51.

[S4] Gálos M, Orosz Á. Ágyazati kőanyagok viselkedésének vizsgálata ismételt terhelés hatására. Sínek Világa 61 2019, p. 10–15.

[S5] Gálos M, Orosz Á, Rádics JP, Tamas K. Diszkrét elemes számítógépes módszer a vasúti zúzottkő ágyazat viselkedésének modellezésére. Sínek Világa 59, 2017, p.22–28.

[S6] Bagi K, Orosz A. A New Variable for Characterising Irregular Element Geometries in Experiments and DEM Simulations. ECMS 2020 Proc. Ed. Mike Steglich Christ. Mueller Gaby Neumann Mathias Walther, ECMS; 2020, p. 256–260. https://doi.org/10.7148/2020-0256.

[S7] Orosz A, Zwierczyk PT. Analysis of The Stress State of a Railway Sleeper Using Coupled FEM-DEM Simulation. ECMS 2020 Proc. Ed. Mike Steglich Christ. Mueller Gaby Neumann Mathias Walther, ECMS; 2020, p. 261–265. https://doi.org/10.7148/2020-0261.

[S8] Orosz A, Tamas K, Radics JP, Galos M. Studying the Behaviour of Crushed Stone Railway Ballast Subjected to Periodic Load. ECMS 2019 Proc. Ed. Mauro Iacono Francesco Palmieri Marco Gribaudo Massimo Ficco, ECMS; 2019, p. 384–388. https://doi.org/10.7148/2019-0384.

[S9] Vajda M.Zs, Olah Z, Orosz A. Evaluating the Stress Field on Sweep During Tillage Process Applying Coupled Finite-Discrete Element Method. ECMS 2019 Proc. Ed. Mauro Iacono Francesco Palmieri Marco Gribaudo Massimo Ficco, ECMS; 2019, p. 358–363. https://doi.org/10.7148/2019-0358.

[S10]           Orosz A, Tamas K, Radics JP, Zwierczyk PT. Coupling Finite and Discrete Element Methods Using an Open Source and a Commercial Software. ECMS 2018 Proc. Ed. Lars Nolle Alexandra Burger Christoph Tholen Jens Werner Jens Wellhausen, ECMS; 2018, p. 399–404. https://doi.org/10.7148/2018-0399.

[S11]           Orosz A, Radics JP, Tamas K. Calibration of railway ballast DEM model. Proc. 31st Eur. Conf. Model. Simul., Budapest, Hungary: European Council for Modeling and Simulation; 2017, p. 523–528. https://doi.org/10.7148/2017-0523.

[S12]           Gálos M, Orosz Á, Rádics JP, Tamás K. Modelling the behaviour of concrete additives via discrete element numerical simulation. Innov. Mater. Technol. Concr. Struct. Proc. Fib Congr., Tokaj, Hungary: Hungarian Group of fib; 2017, p. 607–614.

[S13]           Orosz Á, Zwierczyk PT, Rádics JP, Tamas K. A véges és a diszkrét elemes szimulációk kapcsolásának jelentősége a géptervezésben, Târgu Mureș, Romania: Erdélyi Magyar Műszaki Tudományos Társaság (EMT); 2018, pp. 333–336.

[S14]           Orosz Á, Rádics JP, Tamás K. Zúzottkő diszkrét elemes modelljének létrehozása vasúti pályakarbantartó gépek fejlesztéséhez. OGÉT 2017 XXV Nk. Gép. Konf. 25th Int. Conf. Mech. Eng., Cluj-Napoca: Erdélyi Magyar Műszaki Tudományos Társaság (EMT); 2017, p. 291–294.

 

 

Table of links.

Website of the Department of Machine and Product Design

Website of the Department of Structural Mechanics

Website of Itasca Consulting Group

Website of Itasca Consultants SAS (Itasca France)

Itasca Educational Partnership Research Program

 

List of references.

[1]    EN 13450, Aggregates for railway ballast 2002.

[2]    Liu Y, Gao R, Chen J. Exploring the influence of sphericity on the mechanical behaviors of ballast particles subjected to direct shear. Granul Matter 21 2019, 94. https://doi.org/10.1007/s10035-019-0943-1.

[3]    Zhang T, Zhang C, Zou J, Wang B, Song F, Yang W. DEM exploration of the effect of particle shape on particle breakage in granular assemblies. Comput Geotech 122 2020. 103542. https://doi.org/10.1016/j.compgeo.2020.103542.

[4]    Cundall PA, Strack ODL. A discrete numerical model for granular assemblies. Géotechnique 29 1979. p. 47–65. https://doi.org/10.1680/geot.1979.29.1.47.

[5]    Satake M. Fabric tensor in granular materials. In: Luger VA, editor. Deform. Fail. Granul. Mater., Delft, Netherlands: A. A. Balkema, Rotterdam, Ne; 1982. p. 63–68.

[6]    Angelidakis V, Nadimi S, Utili S. SHape Analyser for Particle Engineering (SHAPE): Seamless characterisation and simplification of particle morphology from imaging data. Comput Phys Commun 265 2021. 107983. https://doi.org/10.1016/j.cpc.2021.107983.

[7]    Cignoni P, Callieri M, Corsini M, Dellepiane M, Ganovelli F, Ranzuglia G. MeshLab: an Open-Source Mesh Processing Tool. In: Scarano V, Chiara RD, Erra U, editors. Eurographics Ital. Chapter Conf., The Eurographics Association; 2008. https://doi.org/10.2312/LocalChapterEvents/ItalChap/ItalianChapConf2008/129-136.

[8]    Eliáš J. Simulation of railway ballast using crushable polyhedral particles. Powder Technol 264 2014. p. 458–465. https://doi.org/10.1016/j.powtec.2014.05.052.

[9]    Šmilauer V, Catalano E, Chareyre B, Sergei D, Duriez J, Gladky A, et al. Yade Documentation. 2nd ed. The Yade Project; 2016.

[10]  PFC - Itasca’s Particle Flow Code Documentation. Minneapolis, USA: Itasca Consulting Group, Inc.; 2018.

[11]  3DEC - 3-Dimensional Distinct Element Code, Online Manual. Minneapolis, USA: Itasca Consulting Group, Inc.; 2016.

[12]  EN 933-3:2012, Tests for geometrical properties of aggregates. Part 3: Determination of particle shape. Flakiness index, Standard 2012.

[13]  EN 933-4:2008, Tests for geometrical properties of aggregates. Part 4: Determination of particle shape. Shape index, Standard 2008.