Vásárhelyi Pál Építőmérnöki és Földtudományok Doktori Iskola 

BME Építőmérnöki Kar, Vízépítési és Vízgazdálkodási Tanszék

Témavezető: Dr. Torma Péter

Tavi légkör–víz határfelület cserefolyamatai

A kutatási téma néhány soros bemutatása

A tavi hidro- és termodinamikai változásokat a lokális meteorológiai folyamatok alakítják a légkör–tó határfelület cserefolyamatain keresztül. Ezen összetett cserefolyamatok a tavi és meteorológiai modellek fontos peremfeltételei, azonban mind a mérésük, mind az elméleti meghatározásuk rendkívül bonyolult, jelentős kihívásokat okoz, ezért a téma nemzetközi szinten is a mikrometeorológiai- és limnológiai kutatások előterébe került.

A kutatóhely rövid bemutatása

Az ELKH-BME Vízgazdálkodási Kutatócsoportja és BME Vízépítési és Vízgazdálkodási Tanszéke (VVT) több évtizede foglalkozik hazai nagy tavaink fizikai és ökológiai folyamatainak feltárásával, mérésével és modellezésével. Ennek keretei között a Balatonon 20 éve üzemeltetnek egy vízminőségi monitoring állomást a part közelében, 2018 óta pedig egy nyíltvízi hidrometeorológiai állomást is.

A kutatás történetének, tágabb kontextusának bemutatása

Tavaink ökoszisztémája, fizikai- kémiai állapota rendkívül érzékenyen reagál a klimatikus változásokra, valamint az egyre jelentősebb antropogén hatásokra. A változások kimenetele bizonytalan, ezek feltárása tudományos vizsgálatot igényel. A klímaváltozás miatt átalakuló meteorológiai folyamatok következtében megváltozik például a tó vízjárása, illetve keveredési és hőmérsékleti viszonyai. Az egyes folyamatok szoros interakcióban vannak, amelynek komplexitását a pozitív és negatív visszacsatolások eredményezik. A tavak hidrometeorológiai állapotát alakító fizikai folyamatok részletes feltárását nagyban segítik a teljes víztestre kiterjedő, mérésekkel igazolt numerikus modellek. Az áramlási és hőmérsékleti dinamikát pontosan szimuláló tavi modell segítségével többek közt a különböző transzportfolyamatok, például az üledékmozgás is számíthatók. illetve eredményei alapján becsülhető, hogy a tó mely részei válhatnak oxigénszegénnyé és lehetnek ezáltal kitéve algavirágzásnak. A különböző modellek azonban csak akkor tudnak megbízható eredménnyel szolgálni, ha a meghajtásukhoz szükséges peremfeltételeket (vagyis meteorológiai meghajtó folyamatokat) kellő pontosággal meg tudjuk határozni.

A kutatás célja, a megválaszolandó kérdések

Doktori kutatásomban a tavi légkör–víz határfelületen történő turbulens impulzuscsere, érzékelhető és párolgási hőcsere vizsgálatával foglalkozom. A cserefolyamatok részletes elemzéséhez ún. örvény-kovariancia (EC) -mérések alapján vezettem le új összefüggéseket. Az impulzusáram meghatározására korábban az oceanográfiai irodalomból ismert összefüggéseket alkalmaztak, melyek azonban tavi körülményekre nem érvényesek. Ennek oka, hogy tavi környezetre jellemző rövid meghajtási hosszak, kis vízmélységek és a kialakuló még fejletlen, fiatal hullámok miatt várhatóan növekszik a vízfelszín ellenállása. Emellett a tavak modellezésekor, a hőcsere-folyamatokat leíró összefüggések paramétereinek becslése során elengedhetetlen a különböző mérési módszerek megközelítésekből eredő hibák számszerűsítése. Ehhez jó támpontot nyújt a tó energiamérlege (EB) és annak zárási hibája. Tavi vízoszlop esetén a teljes elérhető energia a sugárzásból, a víztestben tárolt hőből, valamint a mederhőáramból tevődik össze. Ezek együttesen egyensúlyban vannak a vízfelszínen történő hőcserékkel az EB zárása esetén (1. ábra). Az eddigi legpontosabb hőcseremérés az EC eljárás, amelynek azonban ismert problémája, hogy a légkörben kifejlődő nagyobb léptékű örvényeket nem tudja kimérni, ennek következtében a légkör-víz hőcserét alulbecsüli, mely jelentős zárási hibát eredményez [1]. Az EC-mérés módszertanából adódó EB zárását tavi környezetben még nem vizsgálták a szakirodalomban, ugyanakkor tavi hőmérsékletek modellezéséhez elengedhetetlen.

 

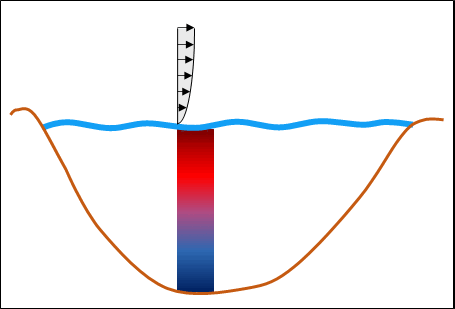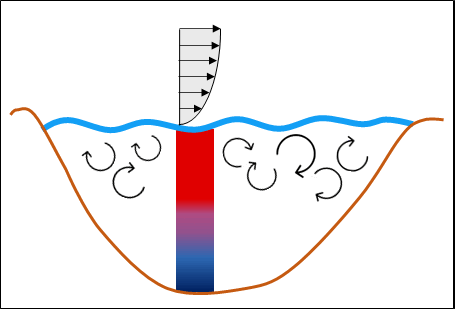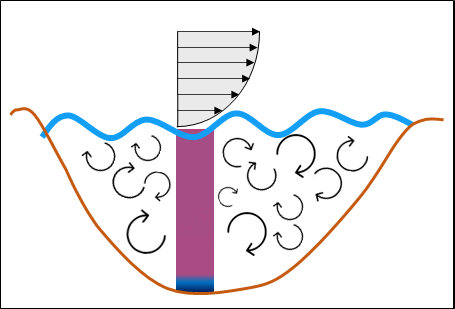
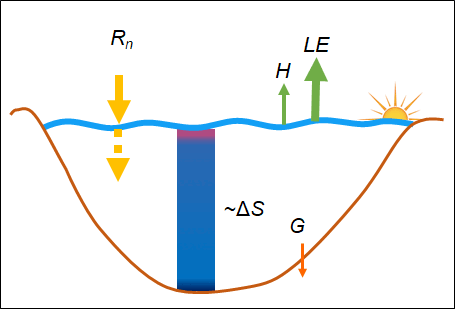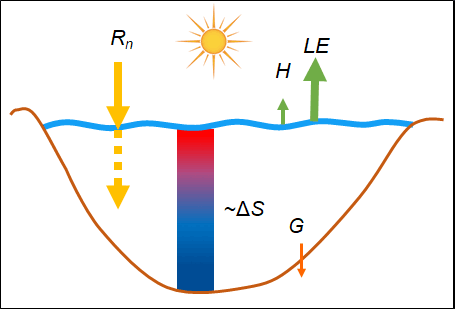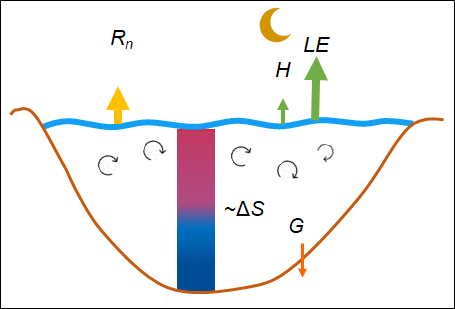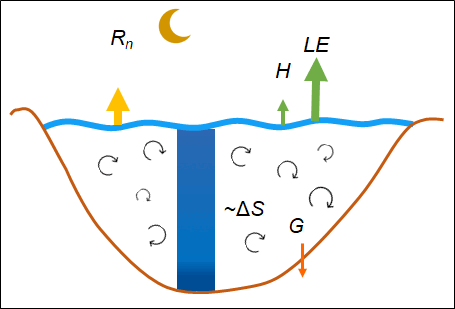
1. ábra: Tavi vízhőmérsékletek és energiamérleg komponensek alakulása egy szeles időszakban (balra) és egy tipikus nyári napon (jobbra)

Módszerek

A szakirodalomban számos elméleti módszer került kidolgozásra a víz–levegő határfelületen zajló turbulens hő- és impulzuscsere számítására, többek között i) a profil alapú fluxus-gradiens módszer, amely a Monin-Obukhov hasonlósági elméleten (MOST) alapszik, ii) az energiaháztartási mérlegen alapuló eljárás, valamint iii) a vízháztartási mérleg alapján történő párolgási hő becslés [2–4]. Kutatásaim során, a mérési adatok alapján fluxus számító paraméterezéseket vezettem le vagy finomítottam tavi környezetre az említett módszerekkel. Ennek érdekében hidrometeorológiai és hullámzásméréseket végeztünk 2019-ben öt hónapon keresztül a Balaton Keszthelyi-medencéjének közepén (2. ábra).

2. ábra: Hidrometeorológiai állomás elhelyezkedése, fotója és műszerezettsége

 

Az örvény-kovariancia műszer nagy frekvencián, közvetlenül mérte a szelet, hőmérsékletet és nedvességtartalmat, amelyből a vizsgálatok középpontjában álló érzékelhető- (H) és párolgási hőáramok (LE), illetve az impulzusáram közvetlenül számíthatók. Ezeken kívül az energiamérleg vizsgálatához mértük továbbá a hosszú- és rövidhullámú sugárzásból adódó nettó sugárzási hőt (R_n), a mélységmenti vízhőmérsékleteket a vízben tárolt hő (ΔS) számításához, valamint a mederhőáramot (G). Az energiamegmaradás szerint az elérhető energiának (R_n+ΔS+G) egyensúlyban kell lennie a vízfelszínen történő cserefolyamatokkal (H+LE). Az energiamérleg zárását a két oldal arányával, azaz az Energy Balance Ratio (EBR) mutatóval fejezhetjük ki:

 

 

Az EB egyenlőtlensége esetén maradéktagot definiálunk, amelyet a zárás eléréséhez szétosztjuk az ún. Bowen-arány (Bo=H/LE) szerint, és így kapjuk meg a EB-korrigált hőcseréket. A hőcserebecslés másik módszeréhez szükséges a Balaton vízmérlegének (WB) ismerete, melynek mérését a Vízügyi Igazgatóság végzi havi léptékben évtizedek óta. A vízmérleg-egyenlet felírásával, a rögzített adatok alapján a tó párolgása számítható:

 

 

 

a víztérfogat-megváltozás (ΔV), csapadék (P), hozzáfolyás (I) és vízkivétel (W), a szabályozott kifolyás (O) segítségével.

Az EC-, az EB- és WB-vel mért és számított cserefolyamatok felhasználásával a fluxus-gradiens eljárás szerint ún. ellenállási (C_D) és átviteli tényezőket (C_H, C_q) határozhatunk meg oly módon, hogy azok közvetlenül becsülhetők legyenek egyszerű rutin időjárási adatok (szélsebesség, hőmérséklet, nedvességtartalom) ismeretében. A tényezők magukba foglalják a vízfelszín aerodinamikai érdességét jellemző érdességi magasságait (z₀, z_0H, z_0q) is, és a légköri rétegzettségtől függő stabilitási függvényeket a MOST szerint.

Eddigi eredmények

Az örvény-kovariancia mérések és hullámzásadatok segítségével vizsgáltam a Monin-Obukhov hasonlósági elmélet szerinti turbulens cserefolyamatok paraméterezését a légkör–víz határfelületen. Az adatokat szigorú minőség-ellenőrzési szűrés alá vetettem, hogy a mérés és a MOST elmélet alapfeltevéseinek eleget tegyenek. A szűrt adatok segítségével impulzuscsere-becslő összefüggéseket vezettem le. A EC-mérések igazolták a hipotézist, miszerint a szakirodalomban fellelhető paraméterezések nem megfelelők balatoni környezetben, ahol a kialakuló hullámok nagyon fiatalok [S1, S2, S4]. Míg az ellenállási tényezők a szélsebesség függvényében növekedtek, addig a hullámkor függvényében csökkentek az irodalmi görbékhez képest (3a-b. ábra). Az aerodinamikai érdességi magasság és a hullámkor között erős kapcsolatot találtam (3c. ábra). A Keszthelyi-medence eltérő részein végzett mérések alapján igazoltuk, hogy az új összefüggéssel az impulzusáram térbeli változékonysága is figyelembe vehető [S1]. Az újonnan levezetett különböző részletességű összefüggésekkel elvégeztem az impulzuscsere becslését, amelyek pontosságát magas determinációs együtthatók jellemezték akár egyszerű becsült hullámzással is.

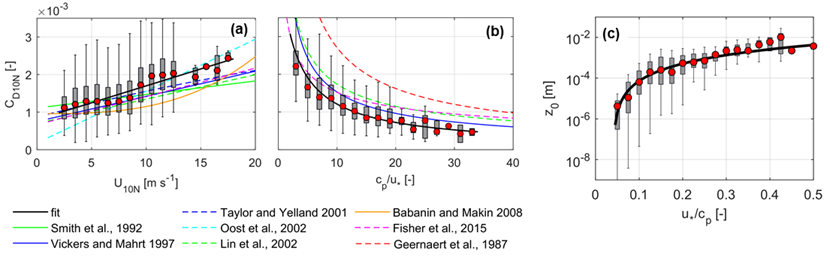
3. ábra: Az ellenállási tényező a szélsebesség (a) és a hullámkor (b) függvényében az irodalmi összefüggésekkel [5-12], az érdességi magasság az inverz hullámkor függvényében (c)

 

Az EB-komponensek és a turbulens hőáramok együttes mérése alátámasztotta a feltételezett számottevő EB-zárási hibát sekély tavi környezetre. Az EB-t különböző időléptékekben vizsgáltam, néhány órástól egészen havi léptékig. Azt tapasztaltuk, hogy nagyobb időléptékben valamelyest javítható az EB zárása, és legalább napi léptékben javasolt az alkalmazása; azonban még havi léptékben is akár 25%-kal alulbecsültek az EC-mérésen alapuló turbulens áramok az elérhető energiamennyiséghez képest [S3, S4]. Emellett a zárási hiba szezonálisan változik, nyáron a legnagyobb. A hőcserékre vonatkozóan is levezettem az átviteli tényezőket az EC-mérések alapján, azonban nagy szórást tapasztaltam, és a különböző meteorológiai változók függvényében is legfeljebb konstans értékkel tudtam jellemezni azokat. A meghatározott konstansok magasabbak, és az arányuk is jelentősen eltér más tavakon mért értékekhez képest. A hőcserék átviteli tényezőinek irodalomban is tapasztalt nagy szórása és az energiamérleg-zárás szezonalitása miatt megvizsgáltam a hőcserékre vonatkozó érdességi magassásokat, amelyek a MOST kulcsparaméterei. Míg az érzékelhető hőcserénél közel állandó (z_0H ~10^‑3 m), addig a párolgáshőnél jelentős szezonális változékonyságot tapasztaltam, amelyek akár két nagyságrendet is változnak (z_0q ~10^-6–10^-4 m) a vizsgált öt hónapos időszak során (4a. ábra) [S4]. Ebből kifolyólag a párolgási hőáramot jellemző átviteli tényező hasonló szezonalitást mutatott. Havi léptékben a párolgáshő becsülhető volt az előbbi módszerektől teljesen független vízmérleg számítás segítségével. Az elérhető tíz év hosszú vízmérlegadatok alátámasztották a teljes éven belüli változékonyságot, ahol akár két és félszerese is lehet a nyári a téli átviteli tényezőnek (5. ábra) [S3].

 

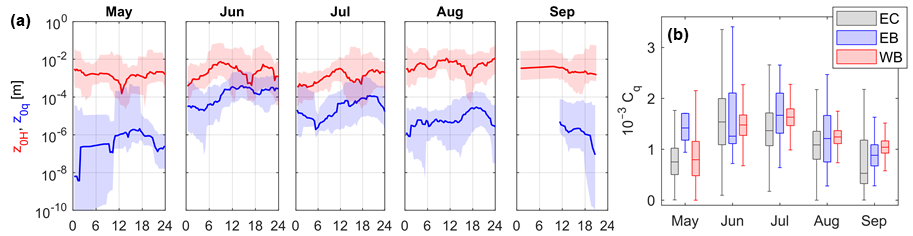
4. ábra: A hőcserék érdességi magasságainak havi és napi menetgörbéi (a) és a párolgáshő átviteli tényezőjének szezonális változékonysága (b)

 

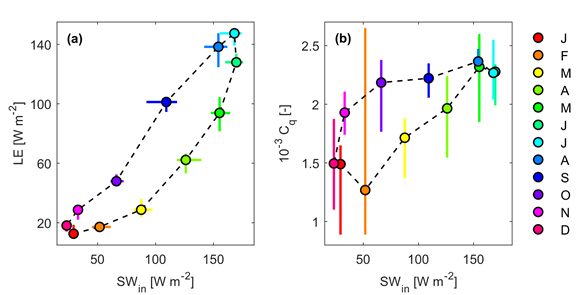
5. ábra: A párolgáshő (a) és átviteli tényezőjének (b) kapcsolata a rövidhullámú sugárzással

 

Más tavakon jellemzően konstansként veszik figyelembe a tényezőket és a szezonális viselkedésüket nem vizsgálják. Ahogy vártuk, a hőcsere EC-alapú meghatározása alulbecsüli azt, így az EB-zárás esetén magasabb átviteli tényezőket kaptunk. A vízmérlegből kapott párolgási átviteli tényezők az EC- és EB-eredmények között helyezkedtek el. Az elvégzett korrelációanalízis azt mutatta, hogy a sugárzási hő a fő meghajtó folyamata a párolgási hő átviteli tényező szezonális változásainak nagyobb (heti és havi) időskálákon. A párolgási hőcserének és tényezőjének a rövidhullámú sugárzással való összevetése során jól kirajzolódó, az éves ciklusra jellemző hiszterézis jellegű kapcsolatot találtunk a tízéves időszakra (5. ábra). A változó átviteli tényezővel történő párolgási hőcserebecslésnél jelentős pontosságnövekedést tapasztaltunk a konstans érték alkalmazásához képest [S3].

Várható impakt, további kutatás

Az új összefüggésekkel egyszerű rutin időjárási adatok alapján pontosabban becsülhető az impulzus- és hőcsere meghajtási hossz-limitált tavi környezetben, így hazai nagy tavainkon is. Összefüggéseink figyelembe veszik a hullámzást, az energiamérleg zárását és a párolgás szezonalitását. Alkalmazásukkal mind a meteorológiai, mind a tavi hidrodinamikai modellek pontosíthatók, hiszen ezáltal pontosabb peremfeltételeket biztosíthatunk számukra. Mindezen eredmények elengedhetetlennek egy megbízható balatoni tavi előrejelző-rendszerhez, amely segítségével a tó hidro- és termodinamikai folyamatai előrejelezhetők, ezáltal többek között az algaprodukcióhoz szükséges állapotok kialakulásának esélye, vagy a már bekövetkezett algásodás térbeli és időbeli alakulása is becsülhető. Egy ilyen modellel egyúttal a klímaváltozás hatása is vizsgálható.

Saját publikációk, hivatkozások, linkgyűjtemény

Kapcsolódó saját publikációk listája.

[S1] Lükő, G., Torma, P., Krámer, T., Weidinger, T., Vecenaj, Z., Grisogono, B. (2020), Observation of wave-driven air-water turbulent momentum exchange in a large but fetch-limited shallow lake, Advances in Science and Research 17, 175–182

[S2] Lükő, G., Torma, P., Krámer, T., Weidinger, T (2021). Hullámzás módosította turbulens impulzusáram mérése és becslése a Balaton légkör-víz határfelületén, Hidrológiai Közlöny 101, 52–60

[S3] Lükő, G., Torma, P., Weidinger, T (2022). Intra-seasonal and intra-annual variation of the latent heat flux transfer coefficient for a freshwater lake, Atmosphere 13, 352

[S4] Lükő, G., Torma, P., Krámer, T., Weidinger, T. (2022), Air-lake momentum and heat exchange in very young waves using energy and water budget closure, Journal of Geophysical Research: Atmospheres 127, e2021JD036099

 

Linkgyűjtemény.

●     BME Vízépítési és Vízgazdálkodási Tanszéke (VVT)

●     Vízminőségi monitoring állomás

●     Visszacsatolások

●     Tavi modell

●     Algavirágzás

●     Örvény-kovariancia

●     Meghajtási hossz

●     Hullámok

●     Monin-Obukhov hasonlósági elmélet

●     Hosszú- és rövidhullámú sugárzás

●     Balaton vízmérleg

 

Hivatkozások listája.

[1] Foken, T. (2008), The Energy Balance Closure Problem: On Overview, Ecological Applications 18(6), 1351–1367

[2] Li, Z., Lyu, S., Zhao, L., Wen, L., Ao, Y., & Wang, S. (2016), Turbulent Transfer Coefficient and Roughness Length in a High-Altitude Lake, Tibetan Plateau, Theoretical and Applied Climatology 124(3–4):723–35

[3] Xiao, W., Liu, S., Wang, W., Yang, D., Xu, J., Cao, C., Li, H., & Lee, H. (2013), Transfer Coefficients of Momentum, Heat and Water Vapour in the Atmospheric Surface Layer of a Large Freshwater Lake, Boundary-Layer Meteorology 148(3):479–94

[4] Xing, Z., Fong, D. A., Tan, K. M., Lo E.Y.-M., & Monismith, S. G. (2012), Water and heat budgets of a shallow tropical reservoir, Water Resources Research 48, W06532

[5] Smith, S. D., Anderson, R. J., Oost, W. A., Kraan, C., Maat, N., De Cosmo, J., Katsaros, K. B., Davidson, K. L., Bumke, K., Hasse, L., & Chadwick, H. M. (1992), Wind Stress and Drag Coefficients, Boundary-Layer Meteorology 60, 109–142

[6] Vickers, D., & Mahrt, L. (1997), Fetch Limited Drag Coefficients, Boundary-Layer Meteorology 85(1), 53–79

[7] Taylor, P. K., & Yelland, M. J. (2001), The dependence of sea surface roughness on the height and steepness of the waves, Journal of Physical Oceanography 31(2), 572–590

[8] Oost, W. A., Komen, G. J., Jacobs, C. M. J., and & Van Oort, C. (2002), New evidence for a relation between wind stress and wave age from measurements during ASGAMAGE, Boundary-Layer Meteorology 103(3)

[9] Lin, W., Sanford, L. P., Suttles, S. E., & Valigura, R., (2002), Drag coefficients with fetch-limited wind waves, Journal of Physical Oceanography, 32(11), 3058–3074

[10] Babanin, A.V., & Makin, V. K. (2008), Effects of wind trend and gustiness on the sea drag: Lake George study, Journal of Geophysical Research 113, C02015

[11] Geernaert, G. L., Larsen, S. E., & Hansen, F. (1987), Measurements of the Wind Stress, Heat Flux, and Turbulence Intensity during Storm Conditions over the North Sea, Journal of Geophysical Research, 92(C12), 127–139

[12] Fisher, A. W., Sanford, L. P., & Suttles, S. E. (2015), Wind Stress Dynamics in Chesapeake Bay: Spatiotemporal Variability and Wave Dependence in a Fetch-Limited Environment, Journal of Physical Oceanography 45(10)