Pál Vásárhelyi Doctoral School of Civil Engineering and Earth Sciences 

Faculty of Civil Engineering, Department of Hydraulic and Water Resources Engineering

Supervisor: Dr. Torma Péter

Exchange processes at the air-water interface of lakes

Introducing the research area

The hydro- and thermodynamics of lakes are driven by the local meteorological characteristics through the exchange processes at the air-lake interface. These processes are important boundary conditions of the lake and meteorological models; however, their measurements and theoretical determination are extremely complicated and challenging; thus, the topic has high research interest internationally in micrometeorology and limnology.

Brief introduction of the research place

The ELKH-BME Water Management Research Group and the BME Department of Hydraulic and Water Resources focus on discovering the physical and ecological processes of large lakes in Hungary using measurements and modeling. In the past 20 years, they have been operating a water quality monitoring station in Lake Balaton close to the shore and since 2018, an offshore hydrometeorological station as well.

History and context of the research

The ecosystem and physical, and chemical conditions of lakes react sensitively to climate change and the increasing anthropogenic effects. The outcome of the changes is uncertain, and they need scientific investigations. The individual processes are in close interaction with each other, and their complexity results in positive and negative feedback loops. Numerical models of the whole water body, verified by measurements, support the analysis of the physical processes that shape the hydrometeorological conditions of lakes. Different transport processes can be calculated using a lake model that simulates the dynamics of currents and temperatures accurately, such as sediment transport. Or, based on model results, it can be estimated which parts of the lake may become anoxic and thus exposed to algal blooms. However, the different models can only provide reliable results if the necessary boundary conditions (the meteorological driving processes) can be accurately determined.

The research goals, open questions

In my doctoral research, I analyze the turbulent momentum, sensible and evaporative (or latent) heat fluxes of the air-water interface of lakes. I derived new formulas for these exchange processes based on the so-called eddy-covariance (EC) measurements. Momentum flux estimation formulas arise from oceanographic literature, which does not apply to lake conditions. Lakes are characterized by short fetches, small depths, and not developed, young waves. These characteristics suggest that the drag of the water surface is increased. Furthermore, in modeling, it is essential to quantify the errors of the different measurement methods when parameterizing the heat flux formulations. The energy balance (EB) and its closing failure are good tools. The available energy for a lake water column mainly consists of radiations, the heat stored in the water body, and the bed heat flux. These are balanced by turbulent heat fluxes at the water surface, and the EB should close (Figure 1). The EC is the most accurate heat flux measurement technique; however, it is known that it cannot measure the developing large-scale eddies in the atmosphere. It mainly underestimates the air-water fluxes resulting in significant closing failures [1]. The EB closure arising from the methodology of the EC measurements has not been analyzed in the literature for lake environment, although it is essential for lake modeling.

 

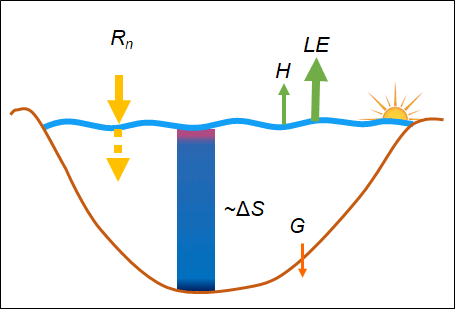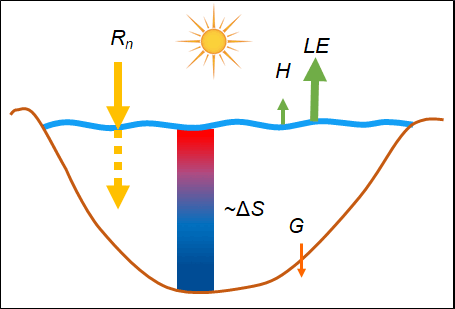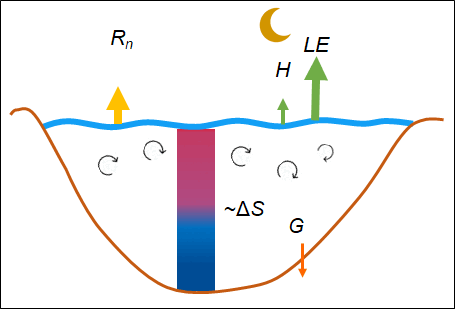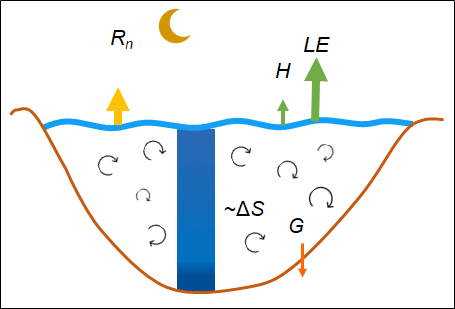
Figure 1. Characteristic lake water temperatures and energy budget components during a wind event (left) and a typical summer day (right).

Methods

There are several theoretical methods for the calculation of the turbulent momentum and heat fluxes at the air-water interface, for example, i) the profile-based flux-gradient method, which is based on the Monin-Obukhov similarity theory (MOST), ii) the energy balance-based method, and iii) the water balance-based evaporative heat estimations [2-4]. In my research, I derived flux calculation parameterizations or refined existing ones to lake environments based on measurement data. We carried out hydrometeorological and wave measurements in 2019 for five months in the middle of the Keszthely basin of Lake Balaton (Figure 2).

Figure 2. The location, photo, and instrumentation of the hydrometeorological station.

 

The eddy-covariance instrument measured the wind speed, temperature, and humidity at very high temporal frequency, from which the momentum flux and the sensible (H) and evaporative heat fluxes (LE) can be directly calculated. Besides these, for the energy balance analysis, the net radiative heat (R_n) from the longwave and shortwave radiation, the water temperatures along the depth to calculate the heat stored in the water (ΔS), and the bed heat flux (G) were measured. According to energy conservation, the available energy (R_n+ΔS+G) must be in balance with the exchange processes (H+LE) at the water surface. The closure of the energy balance can be shown by the ratio of the two sides using the Energy Balance Ratio (EBR):

 

 

In case of energy imbalance, a residual term is defined, which is distributed by the Bowen ratio (Bo=H/LE), resulting in EB-corrected heat fluxes. For the other heat flux estimation method, the knowledge of the water balance (WB) of Lake Balaton is necessary, which has been measured on a monthly scale by the Water Directorate for decades. From the water balance equation and the recorded data, the lake evaporation can be calculated:

 

 

using the change in water volume (ΔV), precipitation (P), inflow (I), water usage (W), and regulated outflow (O).

Using the EC, EB, and WB measured/calculated exchange processes, so-called drag (C_D) and transfer coefficients (C_H, C_q) can be derived according to the flux-gradient method; so, fluxes can directly be estimated later using them, and simple routine weather data (wind speed, temperature, humidity). Based on the MOST, these coefficients can be expressed using roughness lengths (z₀, z_0H, z_0q) characterizing the resistance of the air-water interface and stability functions describing the atmospheric stratification.

Results

Using the eddy-covariance and wave measurements, I analyzed the MOST-based parameterization of the turbulent exchange processes of the air-water interface. The data have been strictly quality-filtered to meet the basic assumptions of the MOST theory. I derived momentum flux estimating formulas using the filtered data. The EC measurements confirmed the hypothesis that the literature parameterizations do not apply to Lake Balaton, where the waves are very young [S1, S2, S4]. While the drag coefficients increased as a function of wind speed, they decreased as a function of wave age compared to literature functions (Figure 3a-b). I found a robust relationship between the aerodynamic roughness length and the wave age (Figure 3c). This new formula can take into account the spatial variability of the momentum flux as was verified by measurements at different locations in the Keszthely basin [S1]. I estimated the momentum fluxes with these differently complex formulas, which resulted in high determination coefficients even in the case of simple wave estimation.

 

 

Figure 3. The drag coefficient as a function of wind speed (a) and wave age (b) with literature functions [5-12], and the aerodynamic roughness length as a function of inverse wave age (c).

 

The synchronized measurement of energy budget components and the turbulent heat fluxes supported the assumed significant EB closure error in the case of a shallow lake. I analyzed the EB on different time scales, from a few hours to one month. I found that the EB closure can be somewhat higher for larger time resolution, and at least a daily scale analysis is suggested. However, even on a monthly scale, the EC-measured heat fluxes are as much as 25% underestimated compared to the available energy [S3, S4]. Besides, the EB closure showed seasonal variability, and the error was most prominent in the summer. I derived the transfer coefficients in the case of the heat fluxes based on the EC measurements. I found a large scatter, and as a result, they could be characterized by constant values as functions of meteorological variables. The derived constants are higher, and their ratio differs from measurements at other lakes. Because of the large scatter expected according to the literature, and the seasonality of the EB closure, I analyzed the roughness lengths for both heat and humidity, the key parameters of the MOST. While the roughness lengths for the sensible heat flux are nearly constant (z_0H ~10^-3 m), in the case of the evaporative heat flux, I found significant intra-seasonal variability of even two magnitudes (z_0q ~10^-6-10^-4 m) during the analyzed five months (Figure 4a). Because of that, the evaporative heat transfer coefficient showed similar seasonality (Figure 4b) [S4]. On a monthly scale, the latent heat flux could be estimated using the WB calculation that is entirely independent of the other methods. The available ten-year-long WB data supported the complete intra-annual variability, where the summer transfer coefficient can be two and a half times higher than the winter one (Figure 5) [S3].

 

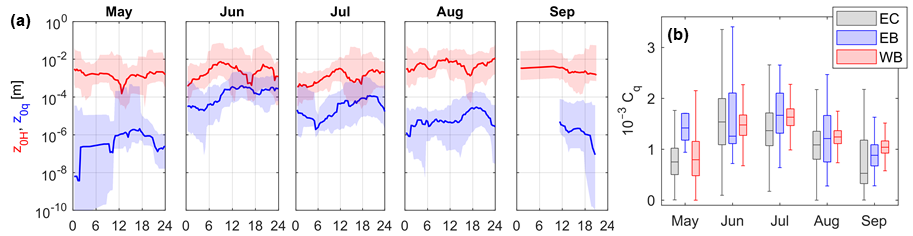
Figure 4. The monthly and daily cycle of heat flux roughness lengths (a) and the seasonal variability of the evaporative heat flux transfer coefficient (b).

 

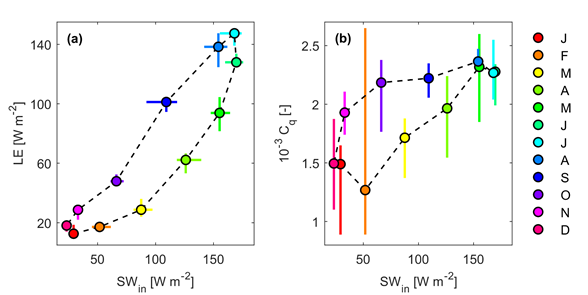
Figure 5. The latent heat flux (a) and its transfer coefficient (b) as a function of shortwave radiation.

 

In the case of other lakes, the coefficients are generally considered constants, and their intra-seasonal variability is not analyzed. As expected, the coefficients were underestimated with the EC-based heat fluxes; thus, they were higher in the case of EB closure (Figure 4b). The coefficients from the WB method were located between the results of the EC and EB methods. The correlation analysis showed that the radiative heat is the primary driver of the evaporative transfer coefficient on larger (weekly and monthly) time scales. The latent heat flux and its transfer coefficient were correlated with the shortwave radiation, and we found well-defined hysteresis characteristics and annual cycles (Figure 5). When applying varying transfer coefficients, the accuracy of the heat flux estimation increased significantly compared to the use of a constant value [S3].

Expected impact and further research

With the new formulas, the momentum and heat fluxes can be estimated accurately by employing simple routine weather data in a fetch-limited lake environment, thus in the large lakes of Hungary. These formulas can account for the effect of waves, the energy balance closure, and the seasonality of evaporation. Implementing them makes both meteorological and lake models more accurate, as more precise boundary conditions can be provided. All these results are essential for a reliable forecasting system for Lake Balaton, which can be used to forecast the lake's hydro- and thermodynamic processes. Such a model can also predict the chance that the conditions necessary for algae production will be reached or the spatial and temporal development of algal growth that has already occurred can also be estimated. With this model, the effect of climate change can also be analyzed.

Publications, references, links

List of corresponding own publications.

[S1] Lükő, G., Torma, P., Krámer, T., Weidinger, T., Vecenaj, Z., Grisogono, B. (2020), Observation of wave-driven air-water turbulent momentum exchange in a large but fetch-limited shallow lake, Advances in Science and Research 17, 175–182

[S2] Lükő, G., Torma, P., Krámer, T., Weidinger, T (2021). Hullámzás módosította turbulens impulzusáram mérése és becslése a Balaton légkör-víz határfelületén, Hidrológiai Közlöny 101, 52–60

[S3] Lükő, G., Torma, P., Weidinger, T (2022). Intra-seasonal and intra-annual variation of the latent heat flux transfer coefficient for a freshwater lake, Atmosphere 13, 352

[S4] Lükő, G., Torma, P., Krámer, T., Weidinger, T. (2022), Air-lake momentum and heat exchange in very young waves using energy and water budget closure, Journal of Geophysical Research: Atmospheres 127, e2021JD036099

 

Table of links.

●       BME Department of Hydraulic and Water Resources

●       Water quality monitoring station

●       Feedback loops

●       Lake model

●       Algal blooms

●       Eddy-covariance

●       Fetch

●       Waves

●       Monin-Obukhov similarity theory

●       Longwave and shortwave radiation

●       Water balance (WB) of Lake Balaton

●       Wave age

 

List of references.

[1] Foken, T. (2008), The Energy Balance Closure Problem: On Overview, Ecological Applications 18(6), 1351–1367

[2] Li, Z., Lyu, S., Zhao, L., Wen, L., Ao, Y., & Wang, S. (2016), Turbulent Transfer Coefficient and Roughness Length in a High-Altitude Lake, Tibetan Plateau, Theoretical and Applied Climatology 124(3–4):723–35

[3] Xiao, W., Liu, S., Wang, W., Yang, D., Xu, J., Cao, C., Li, H., & Lee, H. (2013), Transfer Coefficients of Momentum, Heat and Water Vapour in the Atmospheric Surface Layer of a Large Freshwater Lake, Boundary-Layer Meteorology 148(3):479–94

[4] Xing, Z., Fong, D. A., Tan, K. M., Lo E.Y.-M., & Monismith, S. G. (2012), Water and heat budgets of a shallow tropical reservoir, Water Resources Research 48, W06532

[5] Smith, S. D., Anderson, R. J., Oost, W. A., Kraan, C., Maat, N., De Cosmo, J., Katsaros, K. B., Davidson, K. L., Bumke, K., Hasse, L., & Chadwick, H. M. (1992), Wind Stress and Drag Coefficients, Boundary-Layer Meteorology 60, 109–142

[6] Vickers, D., & Mahrt, L. (1997), Fetch Limited Drag Coefficients, Boundary-Layer Meteorology 85(1), 53–79

[7] Taylor, P. K., & Yelland, M. J. (2001), The dependence of sea surface roughness on the height and steepness of the waves, Journal of Physical Oceanography 31(2), 572–590

[8] Oost, W. A., Komen, G. J., Jacobs, C. M. J., and & Van Oort, C. (2002), New evidence for a relation between wind stress and wave age from measurements during ASGAMAGE, Boundary-Layer Meteorology 103(3)

[9] Lin, W., Sanford, L. P., Suttles, S. E., & Valigura, R., (2002), Drag coefficients with fetch-limited wind waves, Journal of Physical Oceanography, 32(11), 3058–3074

[10] Babanin, A.V., & Makin, V. K. (2008), Effects of wind trend and gustiness on the sea drag: Lake George study, Journal of Geophysical Research 113, C02015

[11] Geernaert, G. L., Larsen, S. E., & Hansen, F. (1987), Measurements of the Wind Stress, Heat Flux, and Turbulence Intensity during Storm Conditions over the North Sea, Journal of Geophysical Research, 92(C12), 127–139

[12] Fisher, A. W., Sanford, L. P., & Suttles, S. E. (2015), Wind Stress Dynamics in Chesapeake Bay: Spatiotemporal Variability and Wave Dependence in a Fetch-Limited Environment, Journal of Physical Oceanography 45(10)