Pattantyús-Ábrahám Géza Gépészeti Tudományok Doktori Iskola 

BME Gépészmérnöki Kar, Műszaki Mechanikai Tanszék

Témavezető: Dr. Insperger Tamás

Gördülő egyensúlyozó deszkán való emberi egyensúlyozás modellezése

A kutatási téma néhány soros bemutatása

Idősödő társadalmunkban egyre gyakoribbak az egyensúlyvesztésből adódó halálos kimenetelű balesetek, amelyeknek hátterében a megnövekedett reakcióidő, az érzékszervek érzékelési pontatlansága, vagy az izomzat gyengülése áll [1]. A balesetek megelőzésében, előrejelzésében kulcsfontosságú az egyensúlyozás mechanizmusának megértése.

A kutatóhely rövid bemutatása

Kutatómunkámat Insperger Tamás témavezetésével végzem a Műszaki Mechanikai Tanszéken az MTA-BME Lendület Emberi Egyensúlyozás Kutatócsoportban. Célunk a központi idegrendszer szabályozási mechanizmusának megértése és modellezése a baleseteket kiváltó tényezők figyelembevételével. Kis szabadsági fokú modellel leírható egyensúlyozási feladatokat vizsgálunk mind elméleti, mint kísérleti módszerekkel és az eredmények alapján egyensúlyfejlesztő eszközöket tervezünk.

A kutatás történetének, tágabb kontextusának bemutatása

Az egyensúlyozás, vagyis a stabilizálás a központi idegrendszer feladata. A vizuális, a vesztibuláris és a szomatoszenzoros rendszerek szemben, fülben, illetve bőrben található receptorai érzékelik, “mérik” az emberi test vagy az egyensúlyozandó tárgy környezethez viszonyított helyzetét, sebességét, gyorsulását. A beérkező információk alapján az agy meghatározza az izomzat egyensúly megtartásához szükséges működését, „utasítást ad” az izomzatnak, amelynek eredménye a korrigáló mozgás. Az információk beérkezése és a szükséges beavatkozás végrehajtása között idő telik el. Ez azt jelenti, hogy a központi idegrendszer a beavatkozást nem az aktuális, hanem múltbeli értékek alapján határozza meg, ezért alul-, vagy túlkompenzál.

Sok hasonlóság figyelhető meg az emberi egyensúlyozás és az iparban alkalmazott szabályozási rendszerek között. Az ipari szabályozók szintén mérést végeznek a stabilizálandó rendszeren, és egy szabályozási elv alapján meghatározzák a szükséges beavatkozást a mérési eredményeket felhasználva. Az egyensúlyozással kapcsolatban a legfőbb, máig megválaszolatlan kérdés az, hogy az agy milyen elv alapján állapítja meg a szükséges beavatkozást, mely iparban is használatos szabályozóval modellezhető. A biomechanika több évtizede foglalkozik ezzel a problémával [2, 3].

A szabályozási mechanizmust általában az egy szabadsági fokkal leírható egy helyben állás példáján keresztül vizsgálják [4-6], azonban egyre több tanulmányban foglalkoznak a mozgó talajon állással. Leggyakrabban egy vezérelhető, a padlóhoz csuklóval kapcsolódó egyensúlyozó deszkával hozzák létre a mozgó felületet, amely természetesen nehezíti az egy helyben állás feladatát [7-9]. Kutatócsoportunk tervezett egy gördülő egyensúlyozó deszkát, amelynek két paramétere változtatható, ezzel költséghatékonyan, vezérlés nélkül befolyásolható az egyensúlyozás nehézsége.

A kutatás célja, a megválaszolandó kérdések

Kutatásom elsődleges célja modellezni és megérteni a központi idegrendszer szabályozási elvét, ezzel feltárni az időskori balesetek pontos okát. A problémát a feladat nehézségének változtatására alkalmas eszközzel, a gördülő egyensúlyozó deszkával vizsgálom. A felállított modell tartalmazza a receptorok által biztosított információk beérkezésének és feldolgozásának időigényét, vagyis a reakcióidőt, valamint az egyes érzékszervek érzékelési bizonytalanságát. Ezen tényezők értéke az egyensúlyozási feladattól és az alanytól függően változhat, becslésükre felépítek egy mérések és számítások összehasonlításán alapuló módszert. Ha sikerül azonosítani, hogy egy adott személynél a reakcióidő vagy az érzékelési pontatlanság növekedése okozza az egyensúlyzavart, akkor célirányosan, a kritikus elemre fókuszáló terápiát, segédeszközt lehet alkalmazni. Kutatásom végső célja egy stratégia kidolgozása az egyensúlyozási mechanizmus kritikus elemének azonosítására.

Az alkalmazott gördülő egyensúlyozó deszka az 1. ábrán látható. Az egyik változtatható paraméter a kerekek sugara (R), a másik az egyensúlyozó deszka lapjának talajtól mért magassága (h). A kialakítás lehetővé teszi mind a sagittalis, mind a frontális síkban való egyensúlyozás vizsgálatát (2. ábra). Önkéntes személyek tapasztalatai szerint csökkentve a kerekek sugarát vagy növelve a lapmagasságot, a feladat egyre nagyobb kihívást jelent. Habár ez a tendencia mindkét síkra igaz, a jelenlegi kutatás eredményei a sagittalis síkra vonatkoznak.

 

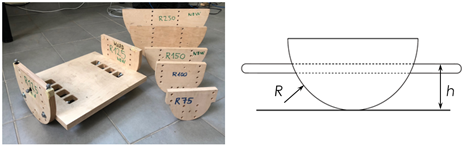
1.      ábra: A kutatásban alkalmazott, változtatható paraméterekkel rendelkező egyensúlyozó deszka.

 

 

2.      ábra: a) Egyensúlyozás a sagittalis síkban. b) Egyensúlyozás a frontális síkban.

Módszerek

A sagittalis síkban való egyensúlyozás két szabadsági fokú mechanikai modelljét (3. ábra) a vizsgálati alanyok tapasztalatai alapján építettem fel. A résztvevők az egyensúlyozáshoz a boka körüli izmokat használták, ezért az agy által meghatározott szabályozó nyomaték, vagyis a beavatkozás a bokánál jelenik meg. Az emberi test mechanikai modellje egy egytagú inverz inga. Különösen nehéz feladat (kis keréksugár, nagy lapmagasság) esetén a törzs döntése is szükséges a stabilizáláshoz, ebben az esetben a vizsgált modell érvényét veszti, tehát egy további szabadsági fokot kellene bevezetni. Az egyensúlyozó deszka súlypontja, tömege, tehetetlenségi nyomatéka kifejezhető zárt alakban a keréksugár és a lapmagasság függvényében. A résztvevők talpa nem emelkedett el egyensúlyozás közben a laptól, következésképpen a két merev test közötti csukló a bokánál található, melynek pozícióját a 3. ábrán az e és az f paraméter jelöli.

 

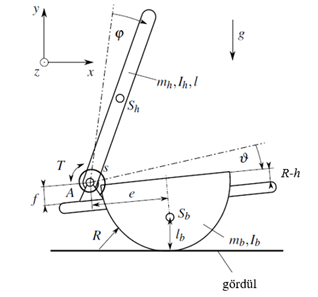
3.      ábra: A sagittalis síkban történő egyensúlyozás két szabadsági fokú mechanikai modellje.

 

A beavatkozó nyomatékot késleltetett arányos-deriváló (PD-) szabályozással modelleztem. A visszacsatolt változók az emberi test és az egyensúlyozó deszka környezethez viszonyított szöge, illetve szögsebessége, ennek megfelelően a szabályozó nyomaték négy konstans, hangolható szabályozó paramétert tartalmaz. A lehető legegyszerűbb modell érdekében a különböző érzékszervek által biztosított információkat ugyanazon konstans, egyenértékű időkéséssel vettem figyelembe.

A rendszer mozgásegyenlete felírható a másodfajú Lagrange-egyenlettel. A felső, instabil egyensúlyi helyzet körüli linearizálás után egy lineáris másodrendű késleltetett differenciálegyenlet-rendszert kapunk. A 3. ábrán szaggatott vonallal jelölt, felső egyensúlyi helyzet stabilitásának feltétele, hogy a karakterisztikus egyenlet összes gyöke a komplex sík bal oldalán helyezkedjen el. A késleltetés miatt a karakterisztikus gyökök száma végtelen, ezért a stabilitásvizsgálat csak összetett módszerekkel, például szemidiszkretizációval, D-szétválasztással, vagy Walton–Marshall-módszerrel lehetséges [10-12].

Ha egy adott egyensúlyozó személyt és adott egyensúlyozó deszkát tekintünk, akkor a karakterisztikus egyenletben a négy szabályozó paraméter és az időkésés szerepelnek mint ismeretlen, hangolható paraméterek. Rögzített időkésés mellett létezik egy véges, négydimenziós tartománya a szabályozó paramétereknek, amelyre a triviális megoldás stabil. Az időkésés növelésével a stabil tartomány mérete csökken, és az ún. kritikus időkésést elérve egy ponttá zsugorodik a négydimenziós térben, majd eltűnik. Az egyensúlyozási kísérleteket tekintve kapcsolat van a kritikus időkésés és a reakcióidő között: ha az egyensúlyozó személy reakcióideje nagyobb, mint az adott egyensúlyozó deszkához tartozó időkésés, akkor stabilizáló paraméterek hiányában a személy biztosan nem képes megállni az egyensúlyozó deszkán.

Eddigi eredmények

Figyelembe véve az érzékszervek érzékelési pontatlanságát, egy új megközelítést vezettem be a kritikus időkésésre (): az a legnagyobb késés, amelyre létezik legalább egy pont a szabályozó paraméterek négydimenziós terében, amelynek tetszőleges tagjait 5%-kal megzavarva stabil marad a rendszer. Az így definiált kritikus időkésés számítására kidolgoztam egy szemidiszkretizáción alapuló algoritmust. A szabályozó paraméterekből, illetve időkésésből álló ötdimenziós paramétertér miatt az algoritmus számításigénye rendkívül nagy, ezért kiemelt figyelmet fordítottam a számítási idő csökkentésére.

Egy adott egyensúlyozó személytömeget és -magasságot, valamint bokapozíciót választva meghatároztam a kritikus időkésést az egyensúlyozó deszka beállítható paramétereire. Az algoritmus eredménye az ún. stabilizálhatósági diagram (4. ábra). A színskála a kritikus időkésés változását mutatja az egyensúlyozó deszka keréksugarának és lapmagasságának függvényében. Ha egy személy egyenértékű reakcióideje 200 ms, akkor a modell szerint csak a kékkel jelölt szintvonal jobb oldalára eső egyensúlyozó deszkákon képes egyensúlyozni, amelyekhez 200 ms-nál nagyobb kritikus időkésés tartozik. Ezt megfordítva, amennyiben ismertek azok a keréksugár–lapmagasság párok, amelyeken egy adott személy képes megállni, becsülhető az egyenértékű reakcióidő.

 

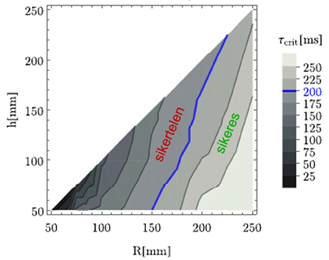
4.      ábra: A stabilizálhatósági diagram segítségével becsülhető a reakcióidő.

 

A becslésre 15 egészséges fiatal felnőtt bevonásával méréseket végeztünk. Először egy pedálos teszt segítségével mértük a vizuális rendszer időkésését fényjel hatására (5. ábra). Ezután meghatároztuk azokat a keréksugarakat a legalsó és legfelső lapbeállítás mellett, amelyeken a vizsgálati alanyok képesek voltak egyensúlyozni. A mechanikai modellnek megfelelően azt a kísérletet tekintettem sikeresnek, amikor a személy képes volt legalább 60 s-ig egyensúlyozni nyitott szemmel, hátratett kézzel, egyenes törzzsel és nyújtott lábbal (2.a) ábra). A sikeres kísérletek azonosításához az emberi testre (vállra, csípőre, térdre) helyezett markereket, OptiTrack mozgáskövető rendszert és egy saját fejlesztésű Matlab-kódot használtam.

 

5.      ábra: Pedálos reakcióteszt.

 

A 6. ábrán látható néhány résztvevő mérési eredménye a stabilizálhatósági diagrammal összevetve. A sikeres próbálkozásokat zöld, a sikerteleneket piros szín jelöli. A sikeres és sikertelen próbálkozások kék határvonala párhuzamos a stabilizálhatósági diagram kontúrvonalaival, az egyenértékű reakcióidő megegyezik a kék vonalhoz tartozó kritikus időkéséssel. A résztvevők becsült reakcióideje 130–170 ms, amely jó egyezést mutat az egy helyben állás szakirodalmi adataival [13-15]. Ebből következik, hogy az időkésleltetett PD-szabályozás egyenértékű reakcióidővel és az 5%-os érzékelési bizonytalansággal megfelelően modellezi a szabályozási mechanizmust.

 

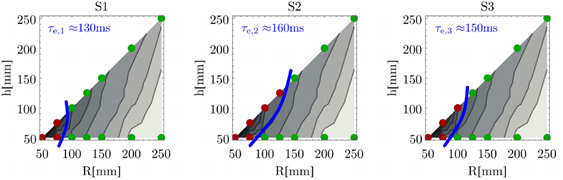
6.      ábra: Három alany mérési eredményei, amelyekből becsülhető az egyenértékű reakcióidő.

 

A legtöbb alany pedálos teszten mért vizuális reakcióideje közelítőleg az egyenértékű reakcióidő kétszerese (7. ábra). Ez azzal magyarázható, hogy az egyensúlyozó deszkán való egyensúlyozás közben a vizuális mellett a vesztibuláris és a szomatoszenzoros rendszerek is támogatják a központi idegrendszert, csökkentve az egyenértékű reakcióidőt. A vizuális és az egyenértékű reakcióidő korrelál, a korrelációs együttható 0,85. Tehát az átlagosnál kisebb vizuális reakcióidővel rendelkező személyek jobb teljesítményt nyújtanak egyensúlyozás közben, amely tapasztalat alapja lehet egy egyensúlyzavar okát azonosító stratégiának. Ha egy egyensúlyzavarral küzdő személy vizuális reakcióideje az átlagosnál kisebb, ennek ellenére gyengén teljesít az egyensúlyozási kísérleteken, feltehetőleg a megnövekedett érzékelési bizonytalanság áll a probléma hátterében.

 

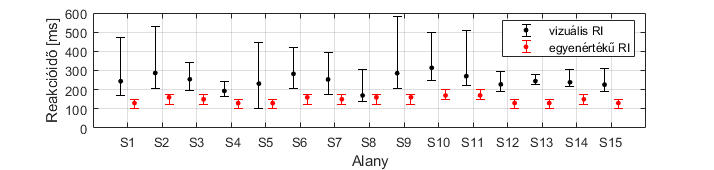
7. ábra: A 15 alany vizuális és egyenértékű reakcióideje a legkisebb és legnagyobb értékekkel.

Várható impakt, további kutatás

A következő cél a frontális síkban való egyensúlyozás modellezése a terpesz nagyság figyelembevételével. Az emberi test legegyszerűbb mechanikai modellje ebben az esetben egy négycsuklós mechanizmus. Jelentősen kevesebb cikkben vizsgálják a frontális síkban történő egyensúlyozást, ezért az egy helyben állás mechanikai modellje is pontosításra vár, amely az ízületek passzív merevségére és csillapítására is kiterjed. A terpesz nagysága feltehetőleg az egyensúlyozó deszkán való egyensúlyozás nehézségét is befolyásolja, az új paraméter tovább növeli a számításigényt, ezért a kritikus időkésést számító algoritmus is további optimalizálást igényel. Megismétlem az egyensúlyozási kísérleteket és reakcióteszteket egyensúlyzavarral küzdő személyek bevonásával, és tovább fejlesztem a stratégiát az egyensúlyvesztést okozó elem azonosítására, ezzel hozzájárulva a balesetek megelőzéséhez.

Saját publikációk, hivatkozások, linkgyűjtemény

Kapcsolódó saját publikációk listája

 

S1.  Molnar CA, Balog T, Boussaada I, Insperger T. Calculation of the critical delay for the double inverted pendulum. Journal of Vibration and Control 2020; 107754632092690, megjelent online.

S2.  Molnar CA, Insperger T. Parametric study of changes in human balancing skill by repeated balancing trials on rolling balance board, Periodica Polytechnica Mechanical Engineering 2020; elfogadva.

S3.  Wang Z, Liang S, Molnar CA, Insperger T, Stepan G. Parametric continuation algorithm for time-delay systems and bifurcation caused by multiple characteristic roots. Nonlinear Dynamics 2020; megjelent online.

S4.  Molnar CA, Insperger T. Estimation of reaction time during human balancing on rolling balance board based on mechanical models. Accepted for the International Design Engineering Technical Conferences & Computers and Information in Engineering Conference 2020; p 8, virtuális konferencia.

S5.  Molnar CA, Insperger T. Egyensúlyozási képességek fejlődésének vizsgálata egyensúlyozó deszkán. in: XIII. Magyar Mechanikai Konferencia 2019; p 4, Miskolc.

S6.  Molnar CA, Varszegi B, Insperger T. Identification of sensory dead zones in human balancing on balance board. in: Proceedings of the European Control Conference (ECC) 2019; 2904–2909., Nápoly.

S7.  Molnar CA, Zelei A, Insperger T. Human balancing on rolling balance board in the frontal plane. in: IFAC-PapersOnLine 2018; 51(14):300–305., Budapest.

S8.  Molnar CA, Zelei A, Insperger T. Mechanical model for human balancing on rolling balance board. Acta Polytechnica CTU Proceedings 2018; 18:32–37.

S9.  Zelei A, Molnar CA, Insperger T. Four-bar mechanism substitution for balance board experiments: A parametric study. in: Proceeding of the Dynamical Systems in Applications 2018; 473–484., Lódz.

S10. Molnar CA, Zelei A, Insperger T. Egyensúlyozó deszkán való egyensúlyozási képességek modellezése a sagittalis síkban. in: OGÉT 2017: 25th International Conference on Mechanical Engineering 2017; 283–286. Kolozsvár.

 

Linkgyűjtemény

 

Műszaki Mechanikai Tanszék honlapja

MTA-BME Lendület Emberi Egyensúlyozás Kutatócsoport honlapja

 

Hivatkozások listája

 

[1]    Robinovitch SN, Feldman F, Yang Y, Schonnop R, Leung PM, Sarraf T, Sims-Gould J, Loughin M. Video capture of the circumstances of falls in elderly people residing in long-term care: an observational study. The Lancet 2013; 381(9860):47–54.

[2]    Woollacott MH, von Hosten C, Rösblad B. Relation between muscle response onset and body segmental movements during postural perturbations in humans. Experimental Brain Research 1988; 72:593–604.

[3]    Kawato M, Furukawa K, Suzuki. A hierarchical neural-network model for control and learning of voluntary movement. Biological Cybernetics 1987; 57:169–185.

[4]    Maurer C, Peterka JP. A new interpretation of spontaneous sway measures based on simple model of human postural control. Journal of Neurophysiology 2005; 93:189–200.

[5]    Insperger T, Milton J, Sépán G. Acceleration feedback improves balancing against reflex delay. Journal of the Royal Society Interface 2013; 10:20120763.

[6]    Asai Y, Tateyama S, Nomura T. Learning an intermittent control strategy for postural balancing using an EMG-based human-computer interface. PLoS ONE 2013; 8(5):e62956.

[7]    Chagdes JR, Rietdyk S, Haddad JM, Zelaznik HN, Raman A. Dynamic stability of a human standing on a balance board. Journal of Biomechanics 2013; 46(15):2593–2602.

[8]    Cruise DR, Chagdes JR, Liddy JJ, Rietdyk S, Haddad JM, Zelaznik HN, Raman A. An active balance board system with real-time control of stiffness and time delay to assess mechanisms of postural stability. Journal of Biomechanics 2017; 60:48–56.

[9]    Chumacero-Polanco E, Yang J. Basin of Attraction and Limit Cycle Oscillation Amplitude of an Ankle-Hip Model of Balance on a Balance Board. Journal of Biomechanical Engineering 2019; 141(11):111007.

[10]  Insperger T, Stepan G. Semi-discretization for time-delay systems, Springer 2011; New York.

[11]  Walton K, Marshall JE. Direct method for tds stability analysis. IEE Proceedings D - Control Theory and Applications 1987; 134(2):101–107.

[12]  Bachrathy D, Stepan G. Bisection method in higher dimensions and the efficiency number, Periodica Polytechnica Mechanical Engineering 2012; 56(2):81–86.

[13]  Beamish D, Bhatti S, Chubbs CS, MacKenzie IS, Wu J, Jing Z. Estimation of psychomotor delay from the Fitts' law coefficients. Biological Cybernetics 2009, 101:279–296.

[14] Goodworth AD, R.J. Peterka RJ. Influence of stance width on frontal plane postural dynamics and coordination in human balance control, Journal of Neurophysiology 2010; 104:1103–1118.

[15] Kiemel T, Zhang Y, Jeka IJ. Identification of neural feedback for upright stance in humans: stabilization rather than sway minimization. Journal of Neuroscience 2011; 31:15144–15153.