Géza Pattantyús-Ábrahám Doctoral School of Mechanical Engineering 

BME GPK, Department of Applied Mechanics

Supervisor: Dr. Insperger Tamás

Modelling of human balancing on rolling balance board

Introducing the research area

In our aging society, the number of fatal falls as a consequence of balance loss is growing significantly. The main causes of falling are the increased reaction time, uncertainty of perception, or weakness of the musculature [1]. Understanding the mechanism of human balancing plays a crucial role in fall prediction and prevention.

Brief introduction of the research place

The current research was carried out at the Department of Applied Mechanics and MTA-BME Lendület Human Balancing Research Group supervised by Tamás Insperger. The main goal of the research group is to understand and model the feedback mechanism of the central nervous system (CNS) considering the factors associated with balance loss. Low-degree-of-freedom balancing tasks are analyzed by theoretical and experimental approach and devices are developed to improve balancing skills.

History and context of the research

The stabilization process of the CNS is as follows. Sensory organs of the visual (eyes), vestibular (ears) and somatosensory (skin) systems measure the position, velocity or acceleration of the body. The brain determines the necessary interaction to maintain balance based on the incoming information, and sends an instruction to the musculature resulting in a corrective movement. The process requires a certain amount of time, the so-called reaction time. Consequently, the necessary interaction is determined based on previously measured values, instead of the actual ones leading to under- or overcompensation. One of the most commonly encountered questions regarding human balancing is how the CNS determines the necessary interaction and which industrial controller is the most appropriate to model its behaviour. Biomechanics has been dealing with this problem for decades [2,3].

The control mechanism is mostly investigated through standing still which can be described by a single-degree-of-freedom mechanical model [4-6]. However, more and more publications focus on balancing on a controllable, pinned balance board [7-9], thus the difficulty of balancing can be influenced arbitrarily by tuning the control of the balance board. For the same purpose, our research team designed a rolling balance board of adjustable geometry. Two parameters of the balance board can be varied; therefore balancing can be analyzed under different conditions cost-effectively, without the need of active control.

The research goals, open questions

The primary goal of my research is to model and understand the control principle of the CNS, thereby diagnosing the critical factor. To realize balancing conditions of different difficulty, the rolling balance board is used. The task-dependent feedback delay and sensory uncertainty are included in the model. To estimate them, a method is constructed using both theoretical and experimental results. The final goal is to create a strategy in order to identify whether the increase of reaction time or sensory uncertainty causes the balance loss. Thus, therapies and devices focusing on the critical element can be applied in a targeted manner.

The rolling balance board is shown in Fig. 1. The adjustable parameters are the radius R of the wheels, and the elevation h of the board measured from the ground. Balancing can be analyzed in the sagittal and frontal planes (Fig. 2.), however, the current results apply to the first one. Experience of preliminary balancing trials performed by volunteers has shown that changing the two parameters has a significant influence on the difficulty of the task. The smaller the radius of the wheels and the greater the distance between the ground and the board, the more difficult the task.

 

Fig. 1: Rolling balance board.

 

Fig. 2: a) Balancing in the sagittal plane. b) Balancing in the frontal plane.

Methods

The two-degrees-of-freedom mechanical model (Fig. 3) is constructed based on the experience of preliminary measurements. Now, we are focusing on easy tasks (large wheel radius, small elevation) when the subjects use the muscles only at the ankle to maintain balance. Consequently, the control torque determined by the brain acts at the ankle and the mechanical model of the human body corresponds to a single inverted pendulum. The center of gravity, mass and moment of inertia of the balance board are expressed in closed form as a function of the wheel radius and the elevation. Participants did not raise their feet from the board during balancing; therefore, the joint between the two rigid bodies corresponds to the ankle, whose position is characterized by parameters e and f (see Fig. 3).

 

 

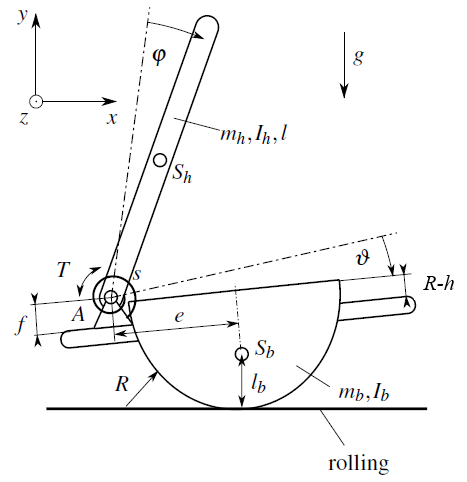
Fig. 3: Two-degrees-of-freedom mechanical model of the analyzed task.

 

The control torque is modeled as a delayed proportional-derivative (PD) controller. The angle and angular velocity of the human body and the balance board are involved in the control torque implying four constant control gains. For the sake of simplicity, the information provided by the different sensory organs is taken into account with the same constant, so-called equivalent time delay.

The equation of motion was written with the help of Lagrange’s equation of the second kind. Linearization around the upper equilibrium results in a system of linear delay differential equations. If all characteristic roots are located on the left half of the complex plane, then the upper equilibrium (denoted by dashed line in Fig. 3) is stable. The number of characteristic roots is infinite due to the presence of delay, therefore the stability analysis requires more advanced methods, such as semi-discretization, D-separation, or Walton-Marshall method [10-12], than that of delay-free systems.

If we consider a certain subject and balance board, the four control gains and the time delay are included in the characteristic equation as unknown parameters. For a fixed time delay, there exists a finite, four-dimensional range of control gains associated with stable trivial solution. As the time delay increases, the size of the stable region shrinks and disappears at the so-called critical feedback delay. In terms of balance trials, the critical delay and the reaction time are related to each other. If the reaction time of a balancing subject is larger than the critical delay associated with a certain balance board, then the subject is unable to stand on that balance board due the absence of stabilizing control gains.

Results

To take into account the sensory uncertainties, a more practical approach of the critical delay was introduced. Namely, the critical delay  is the largest delay associated with a stable system for 5% perturbation of any control gain. To compute the critical time delay for each wheel radius-elevation pair, an algorithm was developed using semi-discretization. Due to the five-dimensional parameter space involving the control gains and the time delay, the computational cost of the algorithm was extremely high.

The critical delays were determined for a fixed human weight, height, and ankle position resulting in the so-called stabilizability diagram (Fig. 4). Gray scale represents the critical delay by varying wheel radius and elevation. If a subject has an equivalent reaction time of 200 ms, then the subject is able to balance on balance boards associated with only the right side of the blue line according to the mechanical model. Thus, the equivalent reaction time can be estimated by comparing the stabilizability diagram and balancing trials.

 

 

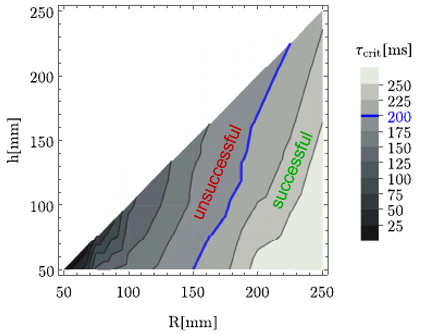
Fig. 4: Stabilizability diagram, and estimation of the reaction time.

 

To validate the model, experiments were performed involving fifteen young healthy adults. First, visual reaction time was measured using a complex reaction time tester (Fig. 5). Then, wheel radii associated with successful balancing were determined both for the bottom and top elevation. Balancing trials were considered successful when the subject was able to stand for at least one minute with open eyes and straight-held body (Fig. 2a). The successful trials were selected using OptiTrack motion capture system and Matlab.

 

 

Fig. 5: Reaction time test.

 

Figure 6 shows the successful trials by green, the unsuccessful ones by red in the stabilizability diagram. The blue boundary between the green and red markers fits the tendency of the stabilizability diagram; therefore the reaction time can be estimated by the critical delay associated with the corresponding contour line. The estimated reaction time of the participants is 130-170 ms. Similar values were obtained for standing still [13-15], therefore time-delayed PD control of 5% uncertainty is a good candidate to model the CNS.

 

 

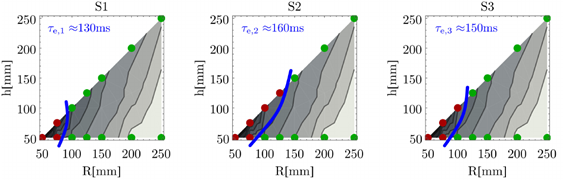
Fig. 6: Estimation of the equivalent reaction time of three subjects.

 

The visual reaction time of all subjects is approximately twice the equivalent reaction time (Fig. 7). This can be explained by the additional support of the vestibular and somatosensory systems while standing on the board. The correlation coefficient is 0.85 which implies that individuals with lower-than-average visual reaction time perform better during balancing. This conclusion can be the basis of a strategy to identify the critical element of the control mechanism. If a subject with balance disorder has a lower-than-average visual reaction time, yet performs weakly during the balancing trials, presumably the increased sensory uncertainty is accountable for the balance loss.

 

 

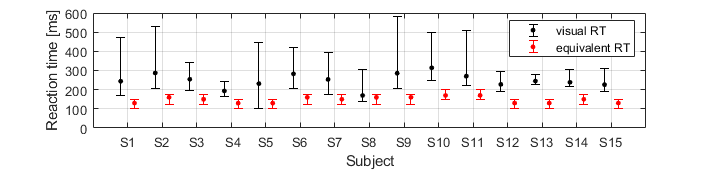
Fig. 7: Visual and equivalent reaction time of the subjects with the maximum and minimum values.

Expected impact and further research

The next stage is the modelling of balancing on balance board in the frontal plane considering the stance width. In this case, the simplest model of the human body is a four bar linkage mechanism. Although the passive stiffness and damping of the hip and ankle joints have also to be determined, the main question remains the effect of stance width. Which helps to stand on challenging balance board configurations, wide or narrow stance? The additional variable involves increasing computational cost; therefore further optimization of the algorithm is required. The measurements will be repeated in the sagittal as well as in the frontal plane. Subjects with balance disorders will also be tested. Based on the results, a strategy will be constructed to identify the critical element, thereby contributing to accident prevention.

Publications, references, links

List of corresponding own publications

 

S1.  Molnar CA, Balog T, Boussaada I, Insperger T. Calculation of the critical delay for the double inverted pendulum. Journal of Vibration and Control 2020; 107754632092690, published online.

S2.  Molnar CA, Insperger T. Parametric study of changes in human balancing skill by repeated balancing trials on rolling balance board, Periodica Polytechnica Mechanical Engineering 2020; accepted.

S3.  Wang Z, Liang S, Molnar CA, Insperger T, Stepan G. Parametric continuation algorithm for time-delay systems and bifurcation caused by multiple characteristic roots. Nonlinear Dynamics 2020; published online.

S4.  Molnar CA, Insperger T. Estimation of reaction time during human balancing on rolling balance board based on mechanical models. Accepted for the International Design Engineering Technical Conferences & Computers and Information in Engineering Conference 2020; p 8, virtual conference.

S5.  Molnar CA, Insperger T. Egyensúlyozási képességek fejlődésének vizsgálata egyensúlyozó deszkán. in: XIII. Magyar Mechanikai Konferencia 2019; p 4, Miskolc, Hungary

S6.  Molnar CA, Varszegi B, Insperger T. Identification of sensory dead zones in human balancing on balance board. in: Proceedings of the European Control Conference (ECC) 2019; 2904-2909., Naples. Italy.

S7.  Molnar CA, Zelei A, Insperger T. Human balancing on rolling balance board in the frontal plane. in: IFAC-PapersOnLine 2018; 51(14):300-305., Budapest, Hungary.

S8.  Molnar CA, Zelei A, Insperger T. Mechanical model for human balancing on rolling balance board. Acta Polytechnica CTU Proceedings 2018; 18:32–37.

S9.  Zelei A, Molnar CA, Insperger T. Four-bar mechanism substitution for balance board experiments: A parametric study. in: Proceeding of the Dynamical Systems in Applications 2018; 473–484., Lodz, Poland.

S10. Molnar CA, Zelei A, Insperger T. Egyensúlyozó deszkán való egyensúlyozási képességek modellezése a sagittalis síkban. in: OGÉT 2017: 25th International Conference on Mechanical Engineering 2017; 283–286. Cluj, Romania.

 

Table of links

 

Department of Applied Mechanics

MTA-BME Lendület Human Balancing Research Group

 

List of references

 

[1]    Robinovitch SN, Feldman F, Yang Y, Schonnop R, Leung PM, Sarraf T, Sims-Gould J, Loughin M. Video capture of the circumstances of falls in elderly people residing in long-term care: an observational study. The Lancet 2013; 381(9860):47–54.

[2]    Woollacott MH, von Hosten C, Rösblad B. Relation between muscle response onset and body segmental movements during postural perturbations in humans. Experimental Brain Research 1988; 72:593–604.

[3]    Kawato M, Furukawa K, Suzuki. A hierarchical neural-network model for control and learning of voluntary movement. Biological Cybernetics 1987; 57:169–185.

[4]    Maurer C, Peterka JP. A new interpretation of spontaneous sway measures based on simple model of human postural control. Journal of Neurophysiology 2005; 93:189–200.

[5]    Insperger T, Milton J, Sépán G. Acceleration feedback improves balancing against reflex delay. Journal of the Royal Society Interface 2013; 10:20120763.

[6]    Asai Y, Tateyama S, Nomura T. Learning an intermittent control strategy for postural balancing using an EMG-based human-computer interface. PLoS ONE 2013; 8(5):e62956.

[7]    Chagdes JR, Rietdyk S, Haddad JM, Zelaznik HN, Raman A. Dynamic stability of a human standing on a balance board. Journal of Biomechanics 2013; 46(15):2593–2602.

[8]    Cruise DR, Chagdes JR, Liddy JJ, Rietdyk S, Haddad JM, Zelaznik HN, Raman A. An active balance board system with real-time control of stiffness and time delay to assess mechanisms of postural stability. Journal of Biomechanics 2017; 60:48–56.

[9]    Chumacero-Polanco E, Yang J. Basin of Attraction and Limit Cycle Oscillation Amplitude of an Ankle-Hip Model of Balance on a Balance Board. Journal of Biomechanical Engineering 2019; 141(11):111007.

[10]  Insperger T, Stepan G. Semi-discretization for time-delay systems, Springer 2011; New York.

[11]  Walton K, Marshall JE. Direct method for tds stability analysis. IEE Proceedings D - Control Theory and Applications 1987; 134(2):101–107.

[12]  Bachrathy D, Stepan G. Bisection method in higher dimensions and the efficiency number, Periodica Polytechnica Mechanical Engineering 2012; 56(2):81-86.

[13]  Beamish D, Bhatti S, Chubbs CS, MacKenzie IS, Wu J, Jing Z. Estimation of psychomotor delay from the Fitts' law coefficients. Biologycal Cybernetics 2009, 101:279–296.

[14]  Goodworth AD, R.J. Peterka RJ. Influence of stance width on frontal plane postural dynamics and coordination in human balance control, Journal of Neurophysiology 2010; 104:1103–1118.

[15]      Kiemel T, Zhang Y, Jeka IJ. Identification of neural feedback for upright stance in humans: stabilization rather than sway minimization. Journal of Neuroscience 2011; 31:15144–15153.