Géza Pattantyús-Ábrahám Doctoral School of Mechanical Engineering 

BME GPK, Department of Applied Mechanics

Supervisor: Dr. Bachrathy Dániel

Stability identification of milling processes by measurement

Introducing the research area

Harmful vibrations in the manufacturing industry can be a barrier to maximizing production. Therefore, the optimal tuning of machining parameters is an extremely important task for professional manufacturers, not only to increase productivity, but also to reduce financial costs [R1]. The biggest challenge of the research is thus the possible prediction of undesirable vibrations before their appearance. This requires the completion of the literature on the identification of machine tool vibrations by measurements.

 

Brief introduction of the research place

The presented research has been carried out at the Department of Applied Mechanics in the MTA-BME Lendület Machine Tool Vibration Research Group under the supervision of Daniel Bachrathy, PhD. The research group is most deeply involved in the development of an appropriate dynamic description technique for machine tool structures, the analysis of vibrations during milling operations and the implementation of possible methods to avoid these vibrations in order to achieve breakthrough in cutting efficiency.

 

History and context of the research

In the manufacturing industry, productivity is a key factor besides quality, efficiency and sustainability. However, productivity cannot be increased arbitrarily due to undesired vibration that may arise during the cutting process. The most critical form of vibrations, chatter can lead to unacceptable surface quality or even damage in the machine–tool structure [R2]. Over the past six decades, numerous studies have addressed productivity and chatter; still many important questions have not yet been answered to date. Therefore, it is essential for mechanical engineers to predict the dynamic behaviour of machining process in order to achieve high material removal rate, thus increase the production rate while avoiding chatter.

From an engineering point of view, the goal is to identify the preferable machining parameters, where chatter does not occur, in the so-called stability chart (see Fig. 1). From this, one can select optimal technological parameters in order to achieve the highest attainable material removal rate – a measure of productivity –, still at acceptable surface quality [R3, J1]. These stability charts are usually illustrated in the plane of the spindle speed and the depth of cut, which parameters are proportional to the material removal rate and thus, to the productivity.

Although the most advanced numerical methods can create the stability charts within seconds [J2], the practical applications still face many problems due to the discrepancies between the predictions and measurements. This is because the mathematical representation of a real dynamical system involves a number of uncertainties, including measurement uncertainties, simplifications on the used models or various other assumptions. The end result is often an unreliable and inaccurate prediction.

 

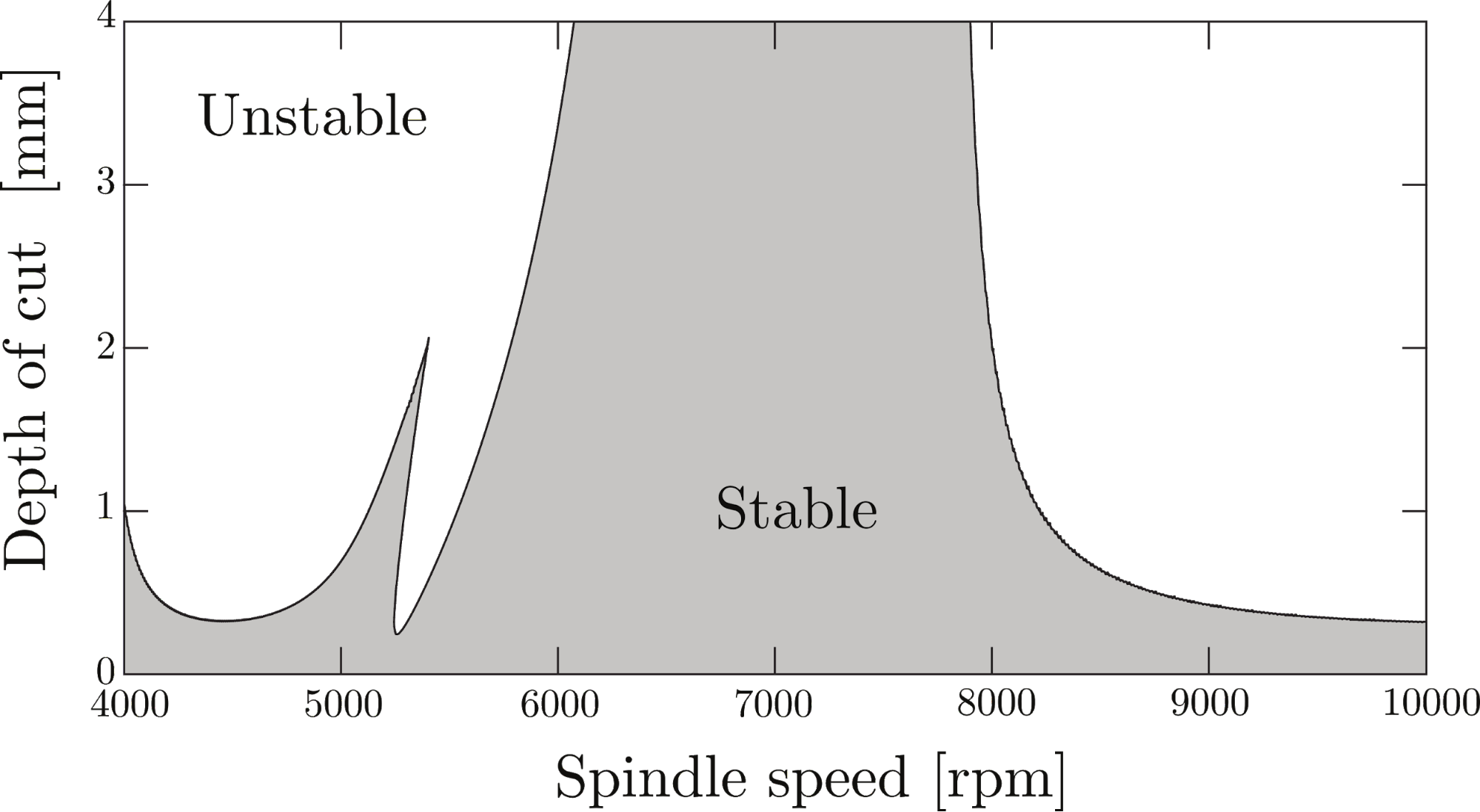
Figure 1 Stability chart: stable and unstable conditions in milling operations

 

The research goals, open questions

The main goal of this research is to characterize the dynamic behaviour of delayed periodic systems (such as the equations modelling the milling operation [R5]) without essential knowledge on the parameters of the underlying mechanical model. In this way, there is no need for modal parameter fitting, which is required for the traditional stability chart calculation methods, and is a major source of inaccurate predictions and model uncertainties. The main idea is to capture the so-called dominant spectral properties – which characterize the behavior – of the system from its impulse response directly [J3, C1].

The results of this main research goal can be used for example, in the operational stability prediction in milling processes [C2]. The new method introduced during the research is able to quantitatively measure the stability of milling operations based on measured resulting vibrations. In the prediction, the stability of the machining process can be characterized through the dominant spectral properties. Because the new method is capable of monitoring how the dominant spectral properties change as a result of technology parameter changes, a precise stability limit can be extrapolated while the manufacturing parameters remain in the safe region, thereby supporting the development of effective milling strategies.

 

Methods

The main research goals described above are therefore:

(i) to characterize dynamical systems without prior knowledge of the model and

(ii) to apply this method for predicting the stability conditions of machining operation.

For the above, two numerical methods have been developed and tested. First, the so-called Impulse Dynamic Subspace (IDS) description [R6] and, second, the Dynamic Mode Decomposition (DMD) [R7] methods.

IDS is an efficient mathematical description for the automatic parameter fitting of mechanical systems. Originally, the method was developed for the investigation of linear time-invariant systems, which is based on the evaluation of frequency response functions by using Green function representation of the homogeneous dynamics. However, in this work, the original ideas of the method had to be slightly modified for use for periodic systems, like milling.

The DMD method is a model reduction and fitting technique based on measurement data. It was originally developed to decompose fluid flows, and then it proved useful in various fields, like studying large-scale neural networks, investigating cyclic behavior of the stock market and pattern recognition in infectious diseases [R7]. The method is capable of approximating the so-called solution operator of periodic systems, which makes it possible to characterize the stability of milling processes.

The methods and their applicability were first tested on an artificial example before applying them in a real measurement environment. In the artificial test case, a time-periodic delay-differential equation (DDE), the so-called delayed Mathieu equation was examined by using time signals generated by numerical integration, as shown in Fig. 2a. Then the efficiency of the methods was demonstrated through a real case study.

 

Results

First, the IDS and DMD methods were tested using the so-called delayed Mathieu equation [C3]. The methods were applied to numerically simulated time signals in order to identify the dominant spectral properties we were looking for. Then they were directly compared to the theoretical ones. As illustrated in Fig. 2, for a sufficient number of discretization, the relevant dominant spectral properties were well approximated by both methods. In the figure, black dots indicate the fitted results, while red ones indicate the theoretical exact values. The correlation between the fitted and the exact theoretical results shows good agreement. Numeric methods could not properly identify low-magnitude spectral properties, which although a disadvantage, from practical point of view, is usually irrelevant in engineering applications.

 

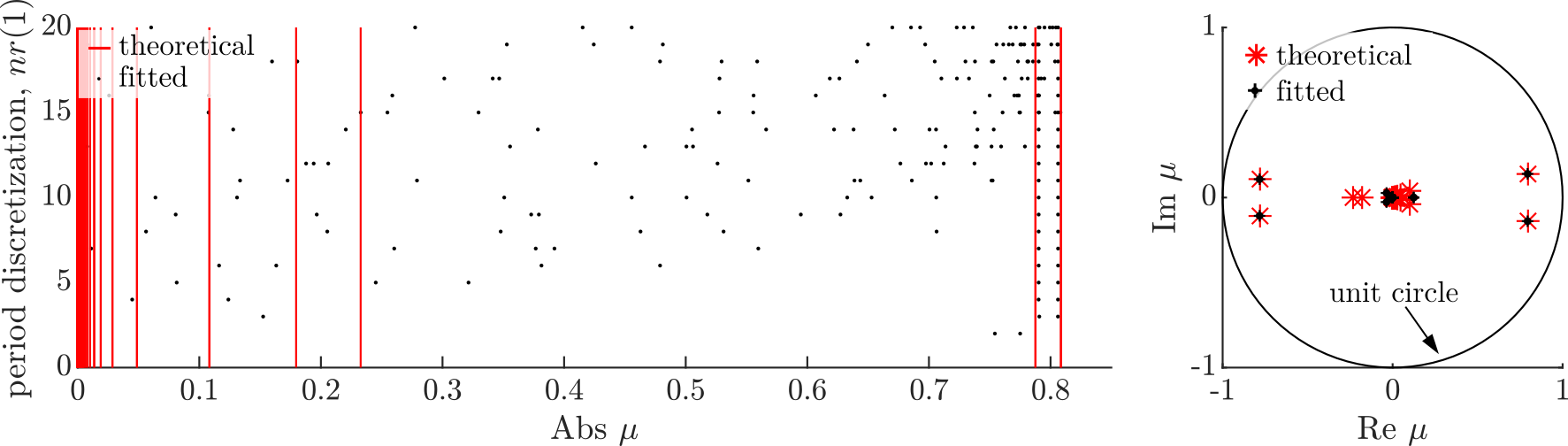
Figure 2 The effect of discretization on the fitted spectral properties for both methods in absolute value and in the complex plane [C3].

 

Then, the above described methods were applied for milling operation in an experimental procedure [J3, C1, C2]. The schematic and the photo of the experimental setup are presented in Fig. 3a. The spectral properties were identified from the transient vibrations of the milling (see Fig. 3b) [J4], which gives a good approximation for the dynamical behaviour of the system. The obtained spectral properties were then compared to the theoretical ones for a set of different cutting speeds, and showed a good correlation, as illustrated in Fig. 3c. Finally, the stability boundary could be precisely determined by means of extrapolation from stable measurement points (see in Fig. 3d).

 

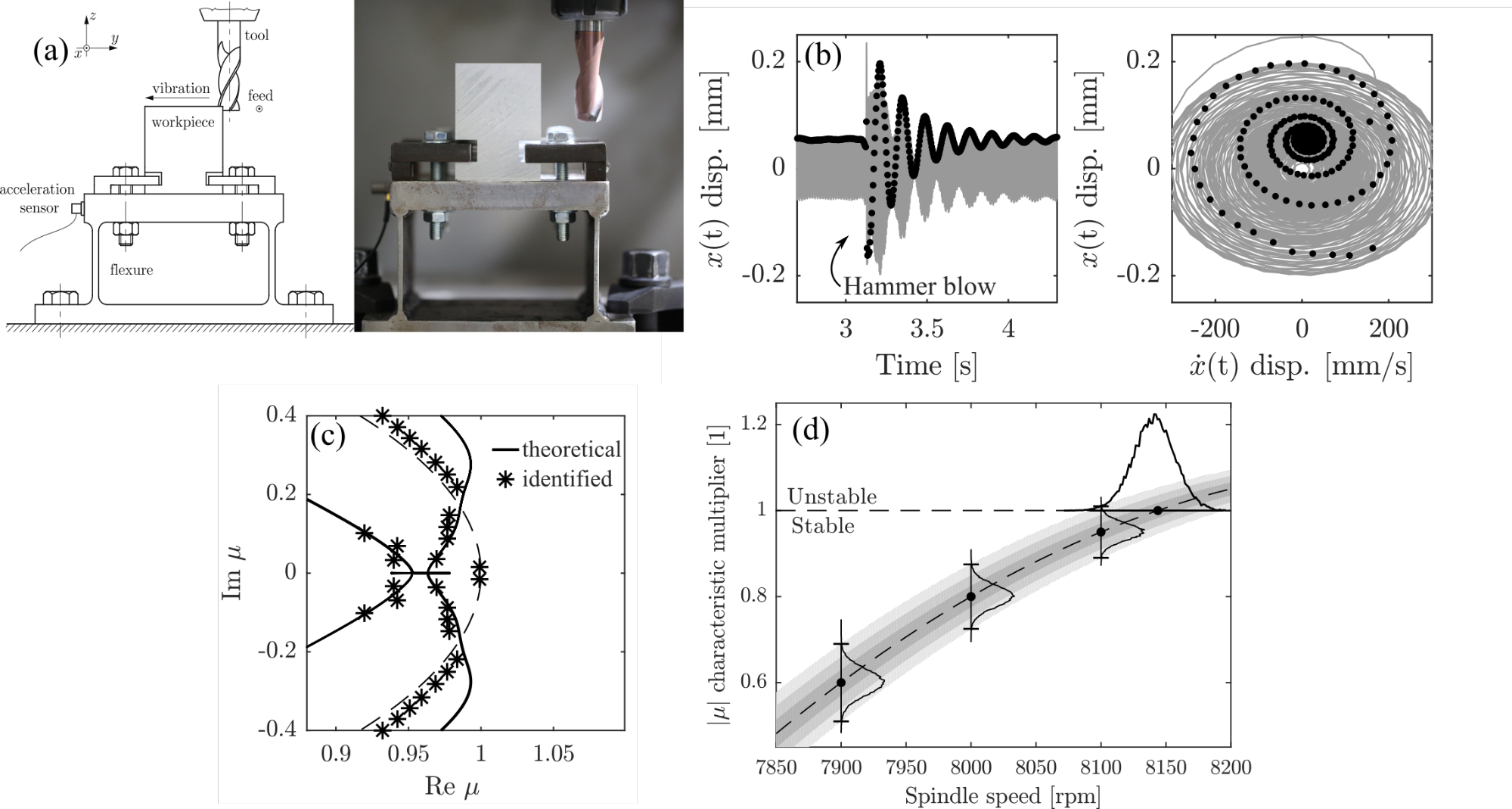
Figure 3 a: The experimental setup; b: time domain of the measured signal; c: identified dominant spectral properties in the complex plane; d: schematic figure representing the extrapolation method of the stability boundary [C2].

 

Expected impact and further research

As the measurement-based indicator currently available in literature distinguishes vibration-free (stable) and harmful (unstable) machining processes in several different ways, it is difficult to compare measurement results with theoretical models. Using the proposed spectral properties as an indicator, the established complex theoretical models can be linked to other measurement methods available for identifying the chatter. In this way, the method is not based on a single experimentally tuned indicator but on the mathematical theory of milling process. Thus, the measurement results can be more accurately compared with the theoretically predicted stability diagrams which is a precondition of testing the practical applicability of the theoretical models.

A future research goal is to automate the proposed procedure, paving the way before possible industrial applications, for example in the automotive, aerospace, manufacturing and energy sectors.

 

Publications, references, links

 

Journal papers:

[J1] A.K. Kiss, D. Bachrathy, G. Stepan, Effects of varying dynamics of flexible workpieces in milling operations, J. Manuf. Sci. Eng., 2020, 142(1): 011005

[J2] G. Stepan, A.K. Kiss, B. Ghalamchi, J. Sopanen, D. Bachrathy, Chatter avoidance in cutting highly flexible workpieces, CIRP Annals – Manufacturing Technology 66(1):377–380, 2017

[J3] A.K. Kiss, D. Hajdu, D. Bachrathy, G. Stepan, Operational stability prediction in milling based on impact tests, Mechanical Systems and Signal Processing 103:327-339, 2017

[J4] D. Bachrathy, A. K. Kiss, A. Kossa, S. Berezvai, D. Hajdu, G. Stepan, In-Process Monitoring of Changing Dynamics of a Thin-Walled Component During Milling Operation by Ball Shooter Excitation, J. Manuf. Mater. Process, 4, 78, 2020

 

Conference papers:

[C1] A.K. Kiss, D. Bachrathy, G. Stepan, Experimental Determination of Dominant Multipliers in Milling Process by means of Homogeneous Coordinate Transformation, Proceedings of ASME 2017, 29th Conference on Mechanical Vibration and Noise, August 6–9, 2017, Cleveland, Ohio, USA, DETC2017-67827

[C2] A.K. Kiss, D. Bachrathy, G. Stepan, Quantitative identification of chatter based on Floquet multipliers in milling operation, 8th International Conference on Virtual Machining Process Technology (VMPT), Vancouver, 23–25 April 2019

[C3] A.K. Kiss, D. Bachrathy, Z. Dombovari, Parameter identification of periodic systems by impulse dynamic subspace description, 10th European Nonlinear Dynamics Conference (ENOC 2020), Lyon, France

 

 

Collection of links

Department of Applied Mechanics

MTA-BME Lendület Machine Tool Vibration Research Group

Daniel Bachrathy, PhD

 

References

[R1] Tobias SA. Machine-Tool Vibration, Blackie & Sons Ltd., London; 1965

[R2] Tlusty J, Spacek L. Self-excited vibrations on machine tools, Prague, Czech: Nakl. CSAV; 1954

[R3] Altintas Y. Manufacturing Automation Metal Cutting Mechanics, Machine Tool Vibrations and CNC Design, 2nd ed. Cambridge, UK; 2012

[R4] Munoa J, Beudaert X, Dombovari Z, Altintas Y, Budak E, Brecher C, Stepan G. Chatter suppression techniques in metal cutting. CIRP Annals, Manufacturing Technology, 62(2):785-808, 2016

[R5] T. Insperger, G. Stepan, Semi-discretization for Time-delay Systems, 178, Springer, New York, 2011.

[R6] Z. Dombovari Dominant modal decomposition method, Journal of Sound and Vibration, 392, 56–69, 2017

[R7] P. J. Schmid, Dynamic mode decomposition of numerical and experimental data. Journal of fluid mechanics, 656, 5–28, 2010