Pattantyús-Ábrahám Géza Gépészeti Tudományok Doktori Iskola 

BME Gépészmérnöki Kar, Műszaki Mechanikai Tanszék

Témavezető: Dr. Bachrathy Dániel

Marási folyamatok stabilitásának méréssel történő azonosítása

A kutatási téma néhány soros bemutatása

A forgácsolási folyamatoknál fellépő nem kívánatos rezgések gátjai lehetnek a termelés maximalizálásának. Emiatt a megmunkálási paraméterek optimális hangolása rendkívül fontos feladat a professzionális gyártók számára, nemcsak a termelékenység növelése, hanem a pénzügyi költségek csökkentése miatt is [H1]. A kutatás legnagyobb kihívása így a nem kívánatos lehetséges rezgések előrejelzése még azok megjelenése előtt, és ehhez szükséges a szerszámgéprezgések méréssel történő azonosításához kapcsolódó szakirodalom bővítése is.

 

A kutatóhely rövid bemutatása

Kutatómunkámat a BME Műszaki Mechanikai Tanszékén belül az MTA-BME Lendület Szerszámgéprezgések Kutatócsoportban végeztem, Dr. Bachrathy Dániel témavezetésével. A kutatócsoport marási folyamatok során fellépő szerszámgéprezgések megfelelő dinamikai leírásával és lehetséges elkerülésük megvalósításával foglalkozik.

 

A kutatás történetének, tágabb kontextusának bemutatása

A tömeggyártásban a minőség, a hatékonyság és a fenntarthatóság mellett a termelékenység is kulcsfontosságú tényező. A termelékenység azonban nem növelhető az egyik legszélesebb körben használt gyártási és termelési eljárásnál, a forgácsolásnál önkényesen az esetlegesen előforduló nem kívánt rezgések miatt [H2]. Ezen káros rezgések legkritikusabb formáját „chatter”-nek nevezzük, amely ronthatja a kialakított felület minőségét, de akár a szerszámgép szerkezetének károsodásához is vezethet. Az elmúlt hat évtizedben számos tanulmány foglalkozott a termelékenység és a szerszámgéprezgések kapcsolatával, mégis számos kérdésre keresi a tudomány a választ napjainkban is. A kialakuló szerszámgéprezgések megbízható előrejelzése fontos feladat a termelékenység növelésének, valamint a felmerülő járulékos költségek és a veszteségek minimalizálásának szempontjából egyaránt.

Mérnöki szempontból a cél azon megmunkálási paramétertartományok kiválasztása, amelyeknél nem lép fel káros rezgés. Ezeket a tartományokat általában az úgynevezett stabilitási térképen szemléltetjük (lásd 1. ábra), ahonnan kiválaszthatók az optimális technológiai paraméterek. Ezeknél érhető el a lehető legnagyobb anyagleválasztási hányad, vagyis a legnagyobb termelékenység, továbbá elfogadható a felületi minőség is [H3, F1]. Ezen stabilitási térképeket rendszerint a fordulatszám és a leválasztott forgácsvastagság függvényében ábrázoljuk, amely paraméterek az anyagleválasztási hányaddal arányosak.

Bár a legfejlettebb módszerek másodperceken belül elkészítik a stabilitási térképeket [F2], a gyakorlati alkalmazásoknál még mindig sok probléma merül fel az előrejelzések és a mérések közötti eltérések miatt [H4]. Az eltérések oka az, hogy a valós dinamikai rendszer matematikai reprezentációja számos bizonytalanságot tartalmaz, kezdve a mérések bizonytalanságaitól az alkalmazott modellek egyszerűsítésein át az egyéb feltételezésekig. Ezek együttes hatása megbízhatatlan és pontatlan előrejelzéseket eredményez.

 

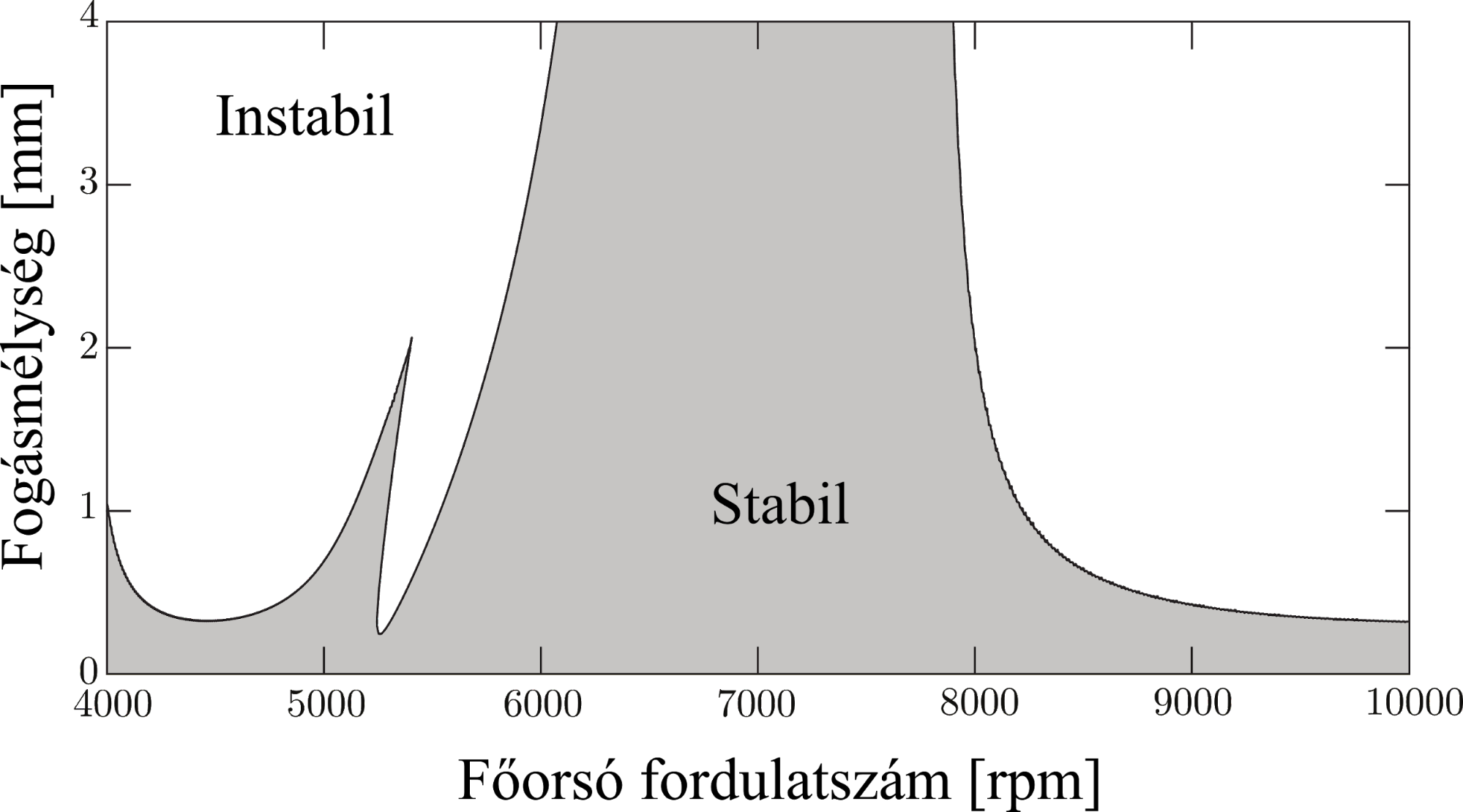
1. ábra: Stabilitási térkép: stabil és instabil megmunkálás

 

A kutatás célja, a megválaszolandó kérdések.

A kutatás fő célja a késleltetett periodikus rendszerek (mint a marást leíró egyenletek [H5]) dinamikai viselkedésének jellemzése az alapjául szolgáló mechanikai modell paramétereinek lényeges ismerete nélkül. Így kiváltható a hagyományos stabilitási térképek számítási algoritmusainak elengedhetetlen kelléke, a modális paraméterek illesztése, amely pontatlan előrejelzéseket és modellbizonytalanságokat eredményezhet. A módszer lényege a rendszer úgynevezett domináns spektrális tulajdonságainak – amelyek karakterizálják a viselkedést – közvetlen meghatározása a rendszert ért impulzusválaszból [F3, K1].

Az említett fő kutatási cél eredményei alkalmazhatók például marási folyamatoknál a stabilitási tulajdonságok mérésen alapuló előrejelzésében [K2]. A kutatás során bevezetett  új módszer képes a marás stabilitásának kvantitatív mérésére a folyamat során keletkező rezgések alapján. Az előrejelzésnél a megmunkálási folyamat stabilitása a domináns spektrális tulajdonságokon keresztül jellemezhető. Mivel az új módszerrel nyomon követhető, hogy miként változnak a domináns spektrális tulajdonságok a technológiai paraméterek változtatásának hatására, így pontos stabilitási határérték prediktálható, és a gyártási paraméterek is a biztonságos tartományban tarthatók, vagyis hatékony marási stratégiák dolgozhatók ki.

 

Módszerek

Az előzőekben leírt fő kutatási célok tehát:

(i) a dinamikai rendszerek megfelelő matematikai leírása az adott modell előzetes ismerete nélkül és

(ii) az így kifejlesztett módszer alkalmazása a forgácsolás stabilitási tulajdonságainak előrejelzésére.

E célok eléréséhez két numerikus módszer lett kidolgozva és tesztelve: először az úgynevezett impulse dynamic subspace (IDS) leírás [H6], majd ezt követően a dynamic mode decomposition (DMD) [H7] módszer.

Az IDS egy hatékony matematikai leírási módszer, amely segítségével elvégezhető mechanikai rendszerek automatikus paraméterillesztése. Eredetileg a módszer lineáris állandó együtthatós rendszerek vizsgálatára lett kifejlesztve, amely a frekvencia-válaszfüggvények kiértékelésén alapszik. Ebben a kutatásban azonban kis mértékben módosítani kellett a módszert, hogy alkalmas legyen periodikus rendszerek leírására, mint amilyen a marás is [K3].

A DMD módszer mérési adatokon alapuló modellredukciós és illesztési eljárás. Eredetileg folyadékok áramlástani vizsgálatára fejlesztették ki, majd idővel több szakterületen is jól használhatónak bizonyult. Ilyenek például a nagy léptékű neurális hálók tanulmányozása, a gazdasági folyamatok és a tőzsde ciklikus viselkedésének vizsgálata, valamint a fertőző betegségek során alkalmazott mintázatfelismerés [H7]. A módszer alkalmas a periodikus rendszerek úgynevezett megoldás operátorának közelítésére, ami lehetővé teszi forgácsolási folyamatok stabilitásának jellemzését.

A módszerek és azok alkalmazhatósága a valós mérési környezetben való alkalmazásuk előtt egy mesterséges példán lett tesztelve. Ennek során egy periodikus késleltetett differenciálegyenlet (DDE), az úgynevezett késleltetett Mathieu-egyenlet lett vizsgálva, numerikus integrálás által generált időjeleket használva. Ezután a módszerek hatékonyságát valós esettanulmányon keresztül demonstráltuk.

 

Eddigi eredmények

Először az IDS és a DMD módszerek tesztelését végeztük el az úgynevezett késleltetett Mathieu-egyenlet segítségével [K3]. A módszereket numerikusan szimulált időjelekre alkalmaztuk a keresett domináns spektrális tulajdonságok azonosítása céljából. Ezt követően az eredményeket közvetlenül összehasonlítottuk az elméletileg várt pontos értékekkel. Ahogyan a 2. ábra is szemlélteti, megfelelő számú diszkretizáció esetén a releváns domináns spektrális tulajdonságokat mindkét módszer jól közelíti, mind a nagyságát, mind a valós és képzetes komponenseit tekintve.  Az ábrán a fekete pontok az illesztett eredményeket jelölik, míg a pirosak az elméleti pontos értékeket. Látható az illesztett és az egzakt elméleti eredmények jó egyezése. A numerikus módszerek a kis értékű spektrális tulajdonságokat nem képesek megfelelően azonosítani, ami bár hátrány, gyakorlati szempontból általában nem releváns a mérnöki alkalmazásokban.

 

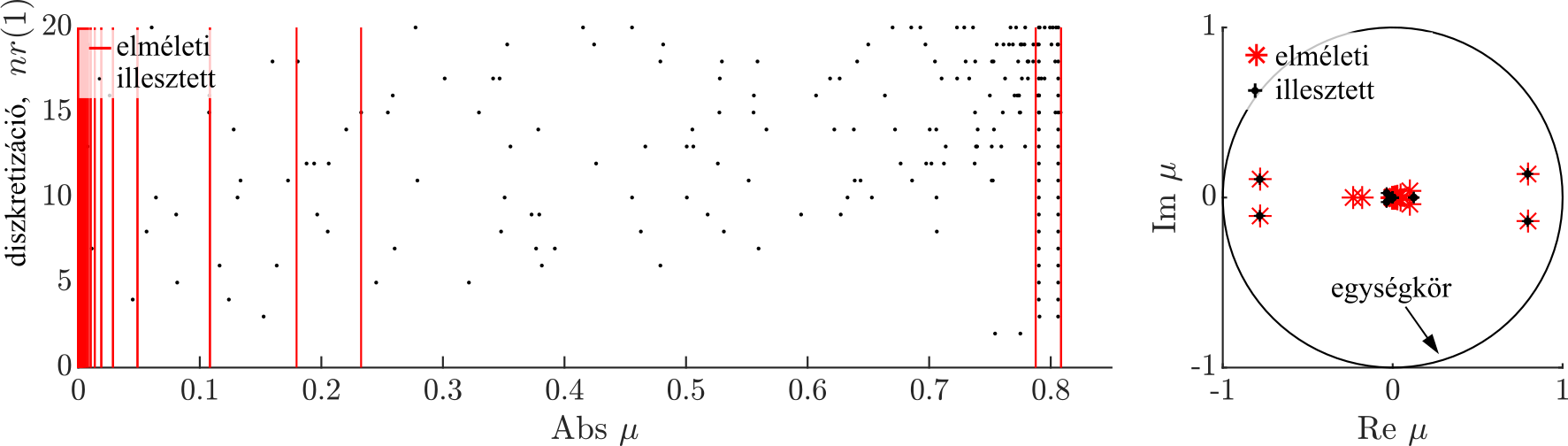
2. ábra: A diszkretizáció hatása a spektrális tulajdonságokra mindkét módszer esetében abszolút értékében és a komplex számsíkon [K3].

 

Ezt követően alkalmaztuk marásra a fentebb bemutatott módszereket egy kísérleti eljárásban [F3, K1, K2]. A mérési elrendezés vázlatát és fényképét a 3a. ábra szemlélteti. A spektrális tulajdonságokat a marás tranziens rezgéseiből határoztuk meg (lásd 3b. ábra) [F4], ami jó közelítés a rendszer dinamikai viselkedésére. A kapott spektrális tulajdonságokat ezután különböző marási fordulatszám-tartományok esetén összehasonlítottuk az elméletileg várt értékkel, és jó egyezést kaptunk, amint azt a 3c. ábra szemlélteti. Végül a stabilitási határ precízen megjósolható volt stabil mérési pontokból történő extrapolációval, ld. 3d. ábra.

 

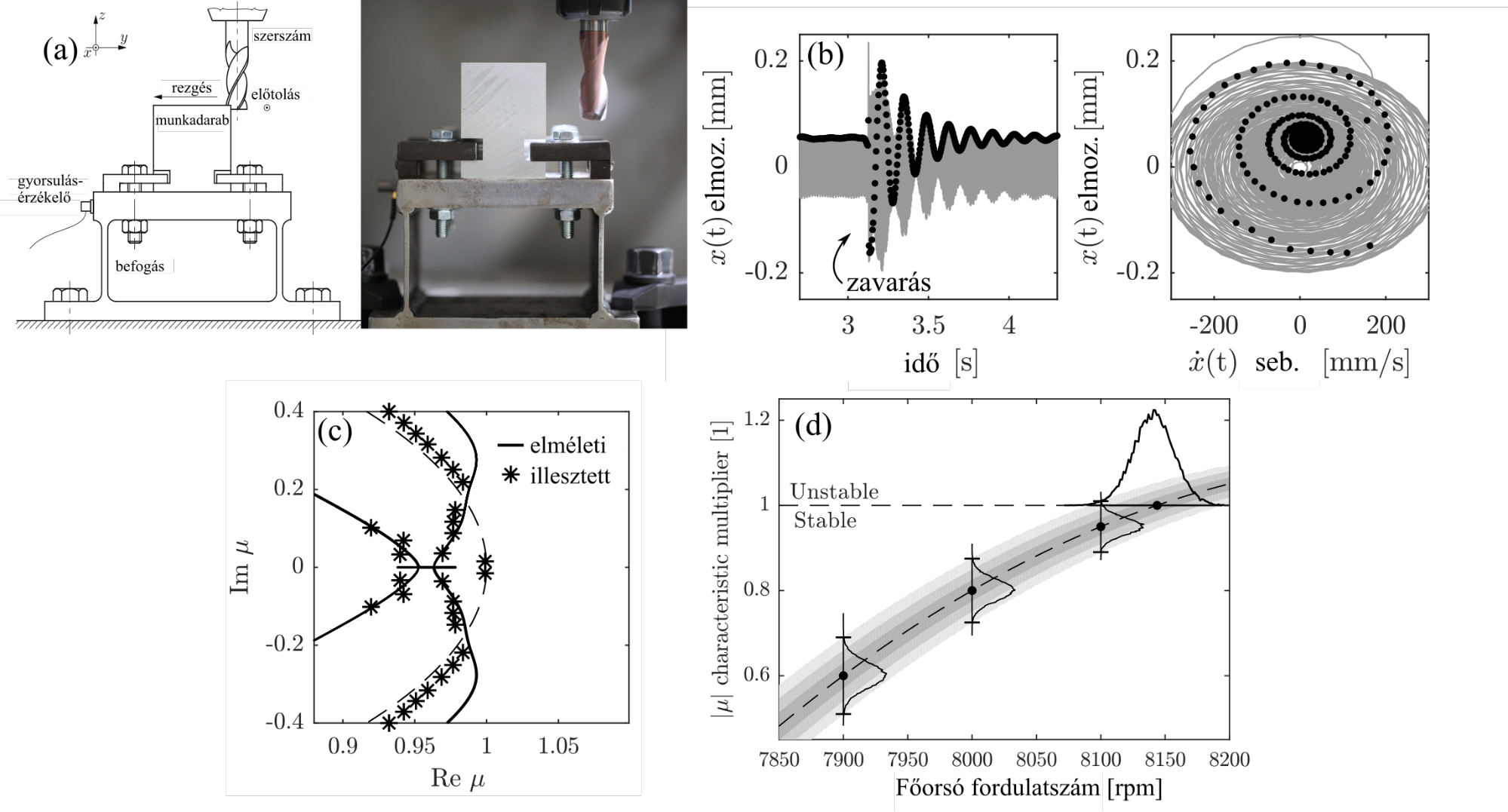
3. ábra: a: A kísérleti berendezés; b: mért időjel; c: azonosított domináns spektrális értékek a komplex számsíkban; d: a stabilitási határ extrapolációs módszerét bemutató sematikus ábra [K2].

 

Várható impakt, további kutatás

A jelenleg elérhető szakirodalom eltérően definiálja azt a mérésen alapuló indikátort, amely megkülönbözteti a rezgésmentes (stabil) és a káros (instabil) megmunkálási folyamatokat, ezáltal nehéz a mérési eredmények elméleti modellekkel történő összehasonlítása. Az általunk definiált spektrális tulajdonságokat indikátorként használva hidat képezhetünk a felállított komplex elméleti modellek és a chatter azonosítására szolgáló egyéb mérési eljárások között, azáltal, hogy a módszer nem egy kísérletileg hangolt indikátoron alapul, hanem a marás folyamatát leíró matematikai elméleten. Így tehát a mérési eredmények pontosabban összehasonlíthatóak az elméletileg előre számított stabilitási diagramokkal, ami elengedhetetlen az elméleti modellek gyakorlati alkalmazhatóságának teszteléséhez.

A jövőbeni kutatási cél a kifejlesztett eljárás automatizálása, ami megteremtheti az iparközeli alkalmazások lehetőségét, például az autóiparban, a repülőgépiparban, a feldolgozóiparban és az energetikai szektorban.

 

Saját publikációk, hivatkozások, linkgyűjtemény

Kapcsolódó saját publikációk listája.

Folyóiratcikkek:

[F1] A.K. Kiss, D. Hajdu, D. Bachrathy, G. Stepan, Operational stability prediction in milling based on impact tests, Mechanical Systems and Signal Processing 103:327–339, 2017

[F2] G. Stepan, A.K. Kiss, B. Ghalamchi, J. Sopanen, D. Bachrathy, Chatter avoidance in cutting highly flexible workpieces, CIRP Annals – Manufacturing Technology 66(1):377–380, 2017

[F3] A.K. Kiss, D. Bachrathy, G. Stepan, Effects of varying dynamics of flexible workpieces in milling operations, J. Manuf. Sci. Eng., 2020, 142(1): 011005

[F4] D. Bachrathy, A. K. Kiss, A. Kossa, S. Berezvai, D. Hajdu, G. Stepan, In-Process Monitoring of Changing Dynamics of a Thin-Walled Component During Milling Operation by Ball Shooter Excitation, J. Manuf. Mater. Process. 2020, 4, 78

 

Konferenciacikkek:

[K1] A.K. Kiss, D. Bachrathy, G. Stepan, Quantitative identification of chatter based on Floquet multipliers in milling operation, 8th International Conference on Virtual Machining Process Technology (VMPT), Vancouver, 2019. április 23–25.

[K2] A.K. Kiss, D. Bachrathy, Z. Dombovari, Parameter identification of periodic systems by impulse dynamic subspace description, 10th European Nonlinear Dynamics Conference (ENOC 2020), Lyon, Franciaország

[K3] A.K. Kiss, D. Bachrathy, G. Stepan, Experimental Determination of Dominant Multipliers in Milling Process by means of Homogeneous Coordinate Transformation, Proceedings of ASME 2017, 29th Conference on Mechanical Vibration and Noise, 2017. augusztus 6–9., 2017, Cleveland, Ohio, USA, DETC 2017-67827

[K4] A.K. Kiss, D. Bachrathy, G. Stepan, Surface Error and Stability Chart of Beam-type Workpiece in Milling Processes, Proceedings of ASME 2016, 28th Conference on Mechanical Vibration and Noise, 2016. augusztus 21–24, 2016, Charlotte, Észak-Karolina, USA, DETC2016-59940

 

 

Linkgyűjtemény.

BME Műszaki Mechanikai Tanszék

MTA-BME Lendület Szerszámgéprezgések Kutatócsoport

Dr. Bachrathy Dániel

 

Hivatkozások listája.

[H1] Tobias SA. Machine-Tool Vibration, Blackie & Sons Ltd., London; 1965

[H2] Tlusty J, Spacek L. Self-excited vibrations on machine tools, Prague, Czech: Nakl. CSAV; 1954

[H3] Altintas Y. Manufacturing Automation Metal Cutting Mechanics, Machine Tool Vibrations and CNC Design, 2nd ed. Cambridge, UK; 2012

[H4] Munoa J, Beudaert X, Dombovari Z, Altintas Y, Budak E, Brecher C, Stepan G. Chatter suppression techniques in metal cutting. CIRP Annals, Manufacturing Technology, 62(2):785–808, 2016

[H5] T. Insperger, G. Stepan, Semi-discretization for Time-delay Systems, 178, Springer, New York, 2011.

[H6] Z. Dombovari Dominant modal decomposition method, Journal of Sound and Vibration, 392, 56–69, 2017

[H7] P. J. Schmid, Dynamic mode decomposition of numerical and experimental data. Journal of fluid mechanics, 656, 5–28, 2010