|
|
BMe Kutatói pályázat |
|
Villamosmérnöki Tudományok Doktori Iskola
BME Villamosmérnöki és Informatikai Kar, Szélessávú Hírközlés és Villamosságtan Tanszék
Témavezető: Dr. Bilicz Sándor
Pilóta nélküli repülőgépek radarral történő felderítése
A kutatási téma néhány soros bemutatása
Az utóbbi időben a pilóta nélküli repülőgépeket – drónokat – egyre gyakrabban használják fel hadi célokra katonai és civil célpontok ellen is, ezért felderítésük egy kiemelkedő fontosságú feladat [1]. A detekcióra használt módszerek közé tartoznak többek között hangalapú [2], vizuális [3] és radart használó módszerek [4], vagy ezek valamilyen kombinációja. A radaralapú megoldásokat nyilvánvaló előnyeik miatt régóta használják repülőgépek, helikopterek felderítésére katonai és civil alkalmazásokban, a drónok felderítése azonban – kis méretükből és radarkeresztmetszetükből (RCS – Radar Cross Section: egy adott céltárgy radar általi „láthatóságát” jellemző, m2 mértékegységű mennyiség) kifolyóan – kihívást jelent, amire jó példa, hogy egy dolgozó a Fehér Ház kertjében le tudott szállni az általa irányított drónnal anélkül, hogy ezt a Fehér Ház automatizált védelmi rendszerei észlelték volna [5].
A kutatóhely rövid bemutatása
A kutatómunkámat az Elektromágneses Mezőszimuláció és Tervezés és a Mikrohullámú Távérzékelés Laboratóriumokkal együttműködésben, a BME Szélessávú Hírközlés és Villamosságtan Tanszékén végeztem.
A kutatás történetének, tágabb kontextusának bemutatása
Ismeretes, hogy amennyiben egy egyenletes mozgást végző testre elektromágneses hullámot irányítunk, a róla szórt tér frekvenciája magasabb vagy alacsonyabb lesz a mozgás irányától függően – ez az ún. Doppler-hatás. Amennyiben a test mozgása nem egyenletes, hanem pl. periodikus, mikro-Doppler-hatásról beszélünk. Ebben az esetben a szórt tér spektruma bonyolultabb alakú is lehet.
A mikro-Doppler-jelenség felhasználásának lehetőségét kis radar-keresztmetszetű repülőgépek észlelésére [6] vizsgálja, és egy megépített kísérleti elrendezéssel demonstrálja egy szénszállal megerősített műanyagból készült, forgó drónpropellerről szóródó tér spektrumában megjelenő komponenseket. Bár a propeller mérete (és radarkeresztmetszete) még a repülőgéptesttel összehasonlítva is kicsi, a forgó mozgást jellemző vonalas, diszkrét szóródási spektrum segítségével azonban könnyebben kiszűrhető a környezet zajából, ami felhasználható lehet a drón lokalizációja céljából.
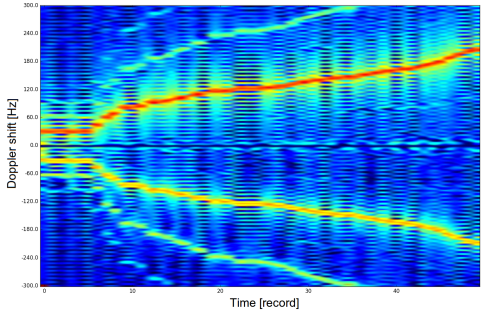
1. ábra: Gyorsuló forgású propellerről szórt tér spektruma az idő függvényében. Megfigyelhetőek a vivőfrekvenciától különböző frekvenciájú komponensek, továbbá az, hogy ezek különbsége a propeller forgási sebességével arányosan növekszik
Periodikus mozgást végző testek és elektromágneses sugárzás kölcsönhatását a szakirodalomban jellemzően frekvenciatartománybeli módszerekkel vizsgálják. Radaralkalmazásokban hasonló szóródási problémák számítására általában fizikai optikai modelleket használnak [7], azonban a kisméretű propellerek esetén, amelyek hossza összemérhető a megvilágítás hullámhosszával, ezen módszerek nem alkalmazhatóak. Ebben az esetben szükséges a Maxwell-egyenletek teljes rendszerének megoldása, a forgás hatásának figyelembevételével.
A kutatás célja, a megválaszolandó kérdések
A tanszéken az érkezésem előtt is kutatómunka folyt a pilóta nélküli repülőgépek radarral történő detekciója területén. Kutatásom célja volt a szénszállal megerősített, kisméretű forgó propellerekről történő elektromágneses szóródás matematikai modelljének kidolgozása, majd a modell validálása reflexiómentes szobában végzett mérésekkel.
A modell létrehozásánál kulcsfontosságú a számítás gyorsasága; egyrészt azért, hogy a forgó propellerek hatékonyan integrálhatóak legyenek egy komplex, az egész repülőt leíró modellbe, továbbá a később részletezett kvázistacionárius közelítés alkalmazása során szükség lehet a szóródást számító függvény sokszori meghívására.
A számítási eredmények validációjára kiváló lehetőségként kínálkozott a tanszéken rendelkezésre álló reflexiómentes szoba igénybevétele. A kísérleteket többféle mérési elrendezésre is végrehajtottam; az egyszerűbb, monosztatikus (az adó- és vevőantennák pozíciója azonos) radardetekción túl bisztatikus (az adó és vevőantanna különböző pozíciókban) mérési elrendezéseket is szükségesnek tartottam vizsgálni, mivel a használt megfigyelési frekvenciatartományban felmerült passzív radarrendszerek használata a drónok észlelésére [8], ugyanis egy tipikus, kb. 25 cm hosszú propeller rezonanciafrekvenciája a DVB-T műsorszórás frekvenciájának közelébe esik.
Az elkészült modellek eredményei alkalmazhatóak lehetnek mind aktív, mind passzív radarrendszerekben; a detekció célja a szórt térben a propeller forgása által keltett vonalas spektrum felismerése, majd a mért értékek alapján a drón lokalizációja.
Módszerek
A forgó propeller és a megvilágító elektromágneses hullám kölcsönhatásának pontos leírása egy összetett feladat, mivel a szórt teret keltő, a propeller mentén a beeső hullám által gerjesztett áramok számítása az elektromágneses térjellemzők forgó koordinátarendszerbe történő transzformációját igényli. A legtöbb műszaki alkalmazásban azonban, lévén a megfigyelt objektumok sebessége a fénysebességhez képest elhanyagolható, a kvázistacionárius közelítés [9], [10] felhasználásával egy nagyon jó pontosságú megoldási sémát állíthatunk fel, melynek segítségével a szórt tér számítása két alfeladatra bontható:
– Statikus céltárgy szóródási modelljének felállítása
– A mozgás figyelembevétele a kvázistacionárius közelítés alapján
A statikus propeller szórt terét két módszerrel vizsgáltam, a végeselem módszerrel [11] és az integrálegyenletek módszerével [12].
Általánosságának és rugalmas alkalmazhatóságának köszönhetően a végeselem-módszer (FEM – Finite Element Method) egy gyakran használt módszer szóródási és egyéb elektromágneses problémák megoldásánál, azonban a szükséges számítási kapacitás sokszor igen magas a térfogati diszkretizáció, a céltárgy méreteinek arányai (például a propeller hossza sokkal nagyobb, mint a szélessége és vastagsága) és a környező térfogat (esetünkben levegő) diszkretizációjának szükségessége miatt. A végeselem-módszer további előnye, hogy segítségével tetszőleges geometriájú és anyagi tulajdonságú céltárgy vizsgálható.
Egy másik lehetőség a vezetőkről történő szóródás modellezésére az integrálegyenlet alapú momentum módszer (MoM --- Method of Moments). A MoM használata előnyös a számítási kapacitás szempontjából, mert akár egyetlen egydimenziós (1D) diszkretizáció is használható; esetünkben a propelleren a hosszanti irányú indukált áramok dominálnak (ez igazolható 3D-szimulációkkal, lásd a 2. ábrát). Ennek következtében sokkal kisebb szabadságfokú problémát kell megoldanunk más numerikus módszerekhez képest, ahol térfogati diszkretizációt használunk (a 3. ábrán látható a FEM-háló). A módszer másik előnye, hogy nem szükséges a propeller környezetének diszkretizációja.
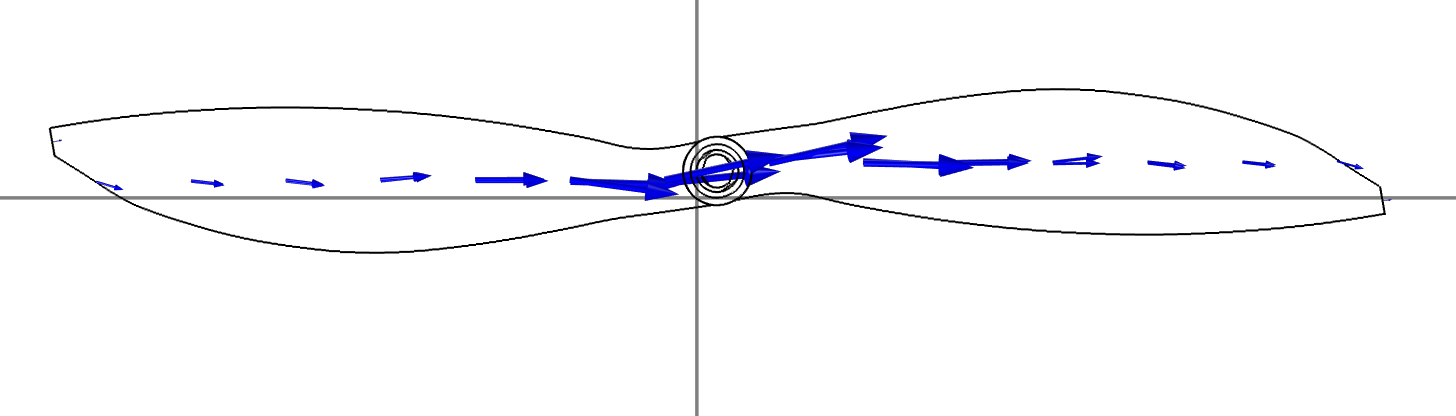
2. ábra: Indukált felületi áramok egy 10 colos propelleren
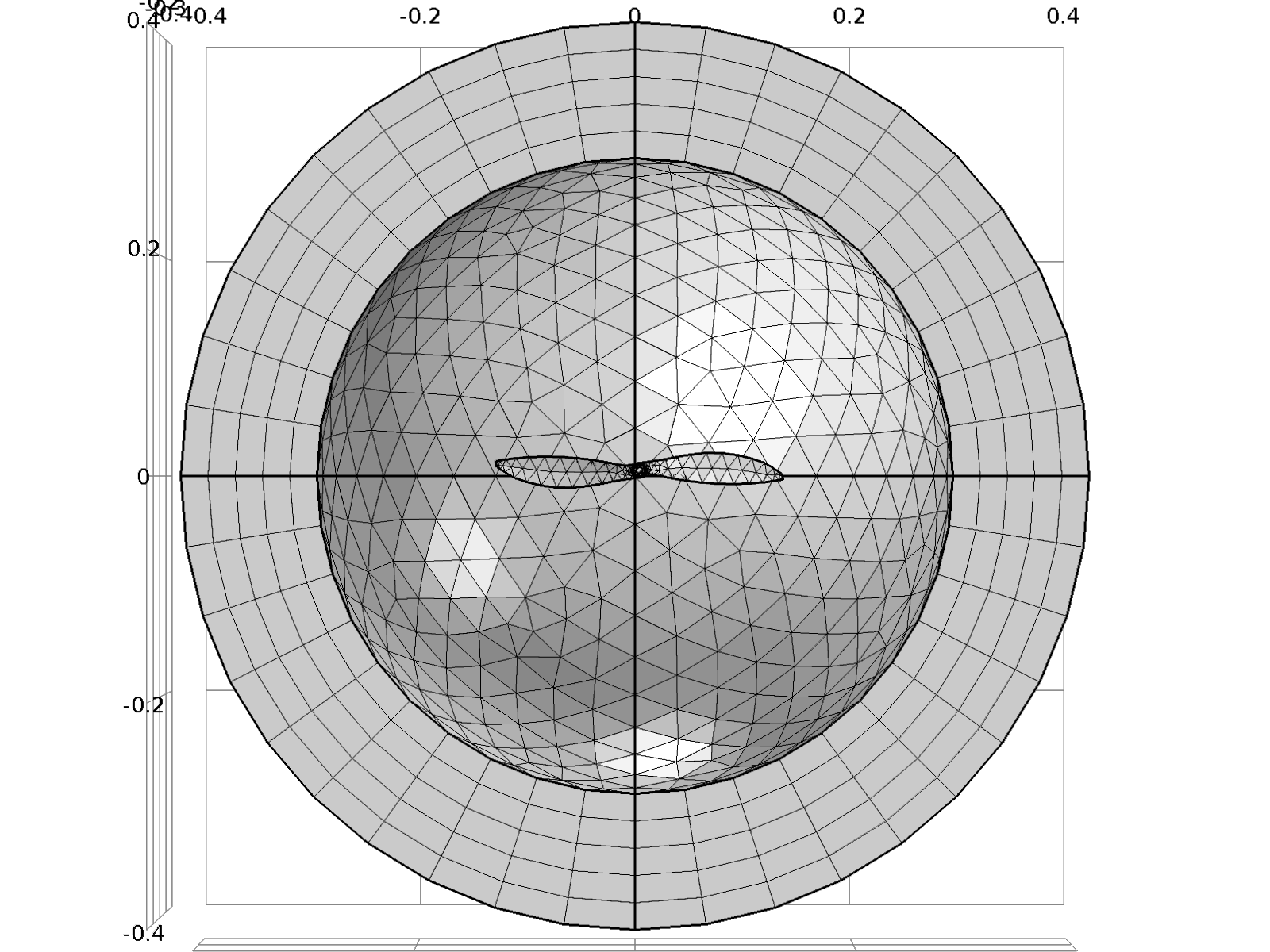
3. ábra: A szóródási szimulációhoz készített végeselem háló. Látható, hogy a módszer használatához szükséges a propeller és a környező levegő térfogati diszkretizációja.
A módszer hátránya, hogy alapesetben ideális vezető peremfeltételt alkalmaz a céltárgyakra; használata ugyan véges vezetőképességű anyagokra is kiterjeszthető, azonban ez további megkötéseket eredményez, ami a modell általánosságát csökkenti. A számítások és mérések eredményei alapján azonban az ez által okozott eltérés a radaralkalmazásokban nem számottevő, és a módszer jó pontossággal alkalmazható.
A FEM-szimulációkat célszoftverben (COMSOL) készítettem el, míg a MoM-kódot és a kísérő számításokat Matlabban írtam meg. A kísérleti berendezést a fentebb említett reflexiómentes szobában (a bisztatikus elrendezés sémája a 4. ábrán látható), továbbá BME V1 épület tetején is felállítottam, így szabadtéri és süketszobás mérési eredmények is rendelkezésemre álltak.
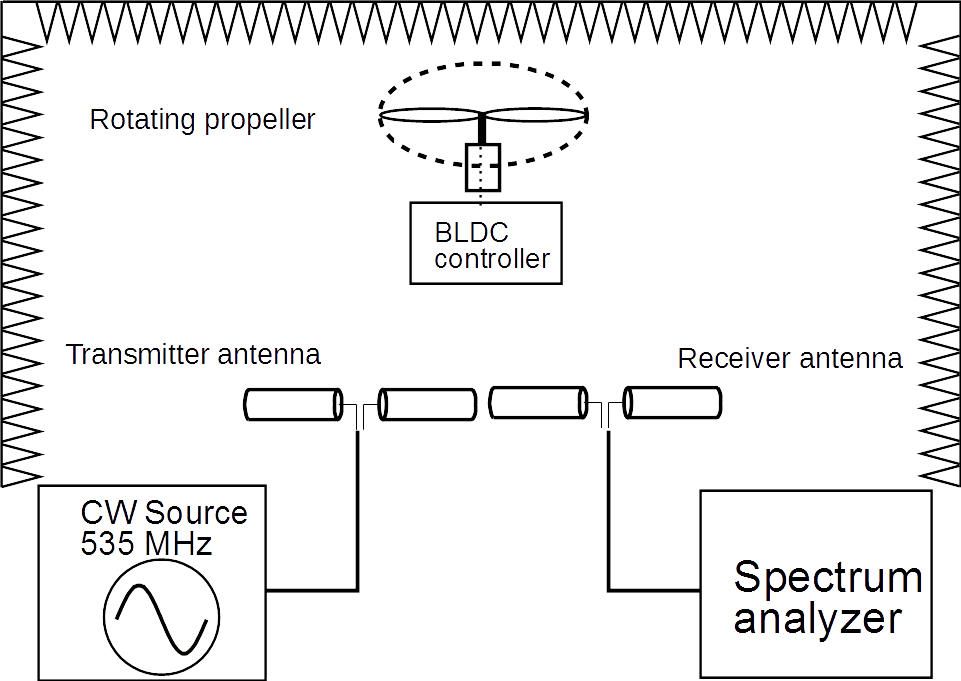
4. ábra: Bisztatikus mérési elrendezés
Eddigi eredmények
Kutatásom első célkitűzése a forgó céltárgyakról történő szóródás elméleti leírása volt. Bár a szakirodalomban foglalkoznak forgó propellerek illetve szélerőmű-lapátok radarkeresztmetszetével (lásd pl. [13], [14]), azonban az itt használt sugárkövetési / fizikai optikai közelítést használó modellek kisebb, a hullámhosszal összemérhető nagyságú céltárgyak – ilyen a vizsgált propeller – esetén nem alkalmazhatók. Ezért kidolgoztam egy olyan módszert, ami a kvázistacionárius közelítést egy tetszőleges térszámítási modellel kombinálva alkalmas egy periodikus mozgást végző céltárgy szóródási spektrumának számítására.
Az első lépésben elkészítettem a szóródás modelljét a propeller néhány, stacionárius orientációjára, amelyek megfelelnek a forgó mozgása közben felvett helyzeteinek. Ezen helyzetek alapján meghatározható a szórt tér forgást leíró szög szerinti komplex Fourier-sora. Munkám során bebizonyítottam, hogy ezen sor együtthatói egyenlők a diszkrét spektrumú szórt térben megfigyelhető frekvenciakomponensek komplex amplitúdóival. Elkészítve a propeller FEM-modelljét, így könnyen meghatározható a szórt tér tetszőleges irányban, ezzel modellezve a monosztatikus és bisztatikus detekciót is. Az eredmények alapos elemzésével arra a következtetésre jutottam, hogy a „klasszikus” mikro-Doppler-effektuson (a céltárgy megfigyelőhöz történő közeledésén/távolodásán) túl hullámhosszal összehasonlítható méretű céltárgyaknál jelentős szerepet játszik a tárgyat a megfigyelővel összekötő szakaszra merőleges síkban történő forgása, mert ennek függvényében erősen változhat a rajta indukálódó áramerősség.
Ezután, a MoM felhasználásával elkészítettem a propeller 1D-s helyettesítő modelljét, majd bebizonyítottam, hogy a hosszúság és átmérő paramétereket a radarkeresztmetszet szerint illesztve viszonylag széles frekvenciatartományban szóródási ekvivalense lesz egy adott propellernek (lásd az 5. ábrát).
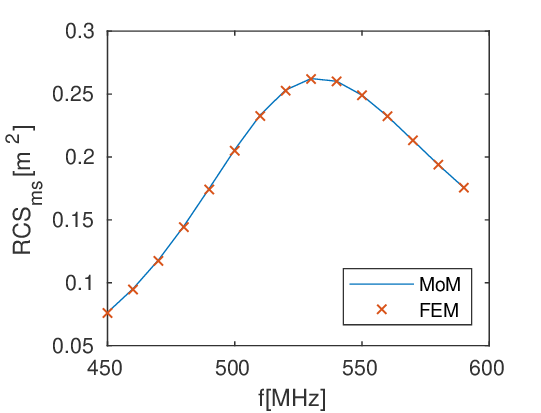
5. ábra: Egy 10 colos propeller végeselem (FEM) és illesztett paraméterű integrálegyenlet (MoM) ‑módszerekkel számolt monosztatikus radarkeresztmetszete a frekvencia függvényében.
Az egyszerű 1D-diszkretizáció segítségével bonyolultabb rendszerek is hatékonyan modellezhetők. Elkészítettem két közeli, különböző szögsebességgel forgó propeller modelljét, ezek spektrumában megjelennek „vegyes” tagok is, amelyek a két propeller kölcsönhatása miatt keletkeznek.
Az elméleti eredmények validálása céljából reflexiómentes szobában (lásd a 6. ábrát), illetve szabadtéren méréseket végeztem. A mérések megerősítik az elméleti előrejelzéseket: megfigyelhető a vonalas spektrum (lásd a 7. ábrát), amely komponenseinek intenzitásai jól egyeznek az elméleti számítások eredményeivel. A kétpropelleres mérések eredményei nagyobb hibával terheltek, azonban a modell kvalitatívan itt is jó eredményt ad, hiszen megfigyelhetők a fentebb említett vegyes tagok a spektrumban (8. ábra).

6. ábra: Bisztatikus mérési elrendezés; az adóantenna (AT) a kép jobb oldalán, a vevőantenna (AR) a kép baloldalán, míg a propeller (S) középen látható.
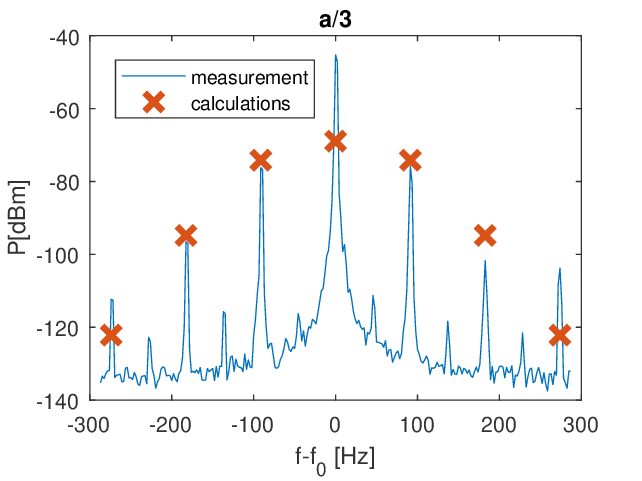
7. ábra: Forgó propeller kísérleti és numerikusan számolt szóródási spektruma bisztatikus szóródásnál. A számítás viszonylag pontosan meghatározza az oldalfrekvenciák intenzitását, a vivőfrekvencián mérhető nagyobb intenzitás a környezetről (főképp a szoba faláról) történő szóródás következménye.
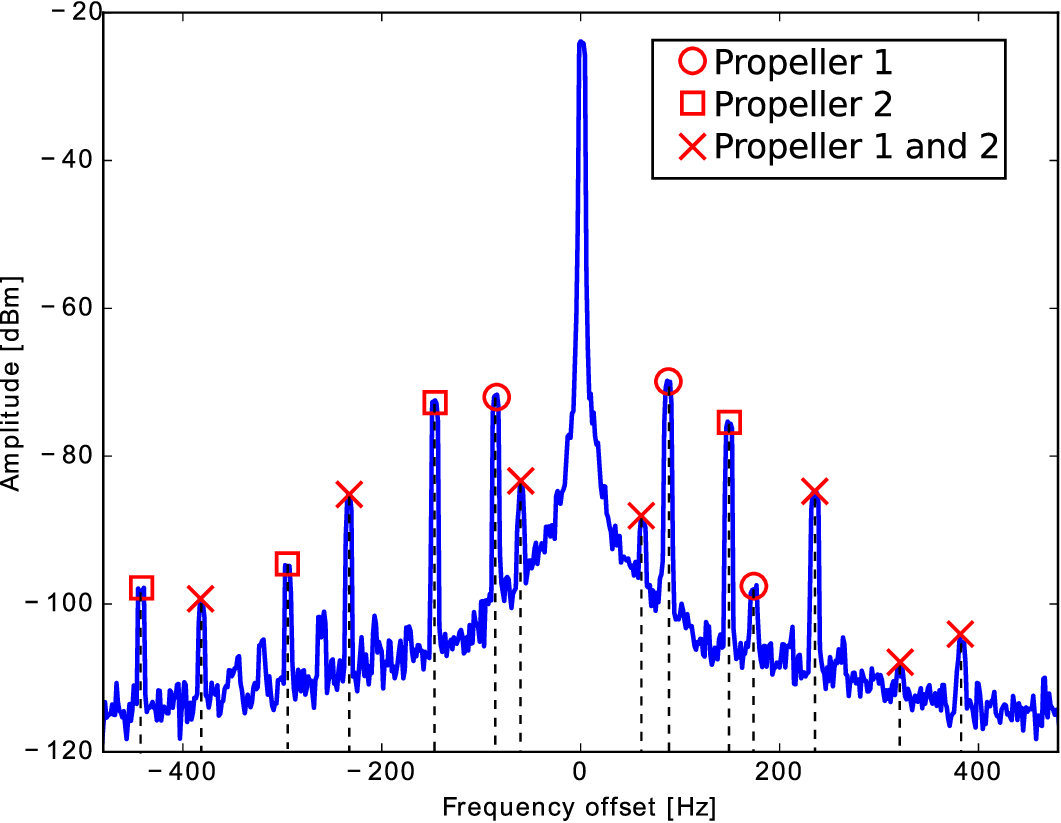
8. ábra: Két, közeli forgó propeller szórt spektruma, 300 mm távolságnál
Várható impakt, további kutatás
A kisméretű, forgó mozgást végző tárgyakról történő szóródást leíró modell alkalmazható drónok radar általi észlelésére, azonban potenciálisan egyéb radaralkalmazásokban is felhasználható; ilyen pl. az autóradarok alagutakban működő ventilátorok által keltett zavara. Mivel a drónpropellerek rezonáns frekvenciája a DVB-T műsorszórás frekvenciája közelébe esik, ezért (különösen a bisztatikus szóródás kapcsán) elért eredményeim hasznosíthatóak drónok passzív radarral való megfigyelése során.
A drónpropellerreken végzett munka során figyelmes lettem arra a tényre, hogy a szóródás matematikai modelljében szerepet játszik a propeller anyagának vezetőképessége. Ennek függvényében változik az adott frekvencián szórt tér intenzitása, továbbá a propeller rezonanciafrekvenciája is. Ez alapján megterveztem egy mikro-Doppler-jelenséget kihasználó kísérleti elrendezést: amennyiben egy ismert geometriájú, hosszúkás alakú mintáról szórt tér intenzitását és/vagy a minta rezonanciafrekvenciát méréssel meg tudjuk határozni, következtetni lehet a minta anyagára. Ebben a témában elért eredményeimet [C5], [J3] -ban publikáltam.
Kapcsolódó saját publikációk
Folyóiratcikkek
[J1] Marák, K., Pető, T., Bilicz, S., Gyimóthy, S., & Pávó, J. (2017). Electromagnetic simulation of rotating propeller blades for radar detection purposes. IEEE Transactions on Magnetics, 54(3), 1–4.
[J2] Marák, K., Pető, T., Bilicz, S., Gyimóthy, S., & Pávó, J. (2018). Bistatic RCS calculation for propellers at near-resonant frequencies. International Journal of Applied Electromagnetics and Mechanics, (Preprint), 1–8.
[J3] Marák, K. Experimental technique for high frequency conductivity measurement, közlésre elfogadva. COMPEL—The International Journal for Computation and Mathematics in Electrical and Electronic Engineering.
Konferenciacikkek
[C1] Marák, K. (2017). Calculation of the radar cross section of small propellers by means of an efficient integral equation method,” in Mesterpróba Proceedings, 20–23.
[C2] Marák, K., Pető, T., Bilicz, S., Gyimóthy, Sz. & Pávó, J. (2017). Electromagnetic simulation of rotating propeller blades for radar detection purposes. Proceedings of Compumag, Daejeon, 1–2.
[C3] Marák, K., Bilicz, S., Gyimóthy, Sz., Pávó, J. & Pető, T. (2017). Bistatic RCS calculation for propellers at near-resonant frequencies. Proceedings of ISEM -- International Symposium on Applied Electrodynamics and Mechanics, 1–1.
[C4] Pető, T., Marák, K., Bilicz, S., & Pávó, J. (2018). Experimental and numerical studies on scattering from multiple propellers of small UAVs. Proceedings of EuCAP, 1–4.
[C5] Marák, K., Bilicz, S., & Pávó, J. (2018). Experimental technique for high frequency conductivity measurement,” Proceedings of IGTE Symposium, 1–1.
Hivatkozások
[1] Sturdivant, R. L., & Chong, E. K. (2017). Systems engineering baseline concept of a multispectral drone detection solution for airports. IEEE Access, 5, 7123–7138.
[2] Nijim, M., & Mantrawadi, N. (2016, May). Drone classification and identification system by phenome analysis using data mining techniques. In 2016 IEEE Symposium on Technologies for Homeland Security (HST) (pp. 1-5). IEEE.
[3] Rozantsev, A., Lepetit, V., & Fua, P. (2016). Detecting flying objects using a single moving camera. IEEE transactions on pattern analysis and machine intelligence, 39(5), 879–892.
[4] Drozdowicz, J., Wielgo, M., Samczynski, P., Kulpa, K., Krzonkalla, J., Mordzonek, M., .& Jakielaszek, Z. (2016, May). 35 GHz FMCW drone detection system. In 2016 17th International Radar Symposium (IRS) (pp. 1-4). IEEE.
[5] https://www.nytimes.com/2015/01/27/us/white-house-drone.html, 2019.06.19
[6] Pető, T., Bilicz, S., Szűcs, L., Gyimóthy, S., & Pávó, J. (2016, April). The radar cross section of small propellers on unmanned aerial vehicles. In 2016 10th European Conference on Antennas and Propagation (EuCAP) (pp. 1–4). IEEE.
[7] Chen, V. C., Li, F., Ho, S. S., & Wechsler, H. (2006). Micro-Doppler effect in radar: phenomenon, model, and simulation study. IEEE Transactions on Aerospace and electronic systems, 42(1), 2–21.
[8] Daun, M., Nickel, U., & Koch, W. (2012). Tracking in multistatic passive radar systems using DAB/DVB-T illumination. Signal Processing, 92(6), 1365–1386.
[9] Cooper, J., & Wilcox, C. H. (1980). Scattering by moving bodies: the quasi stationary approximation. Mathematical Methods in the Applied Sciences, 2(2), 131–148.
[10] Van Bladel, J. (2012). Relativity and engineering (Vol. 15). Springer Science & Business Media.
[11] Jin, J. M. (2015). The finite element method in electromagnetics. John Wiley & Sons.
[12] Gibson, W. C. (2007). The method of moments in electromagnetics. Chapman and Hall/CRC.
[13] Yang, S. Y., Yeh, S. M., Bor, S. S., Huang, S. R., & Hwang, C. C. (1997). Electromagnetic backscattering from aircraft propeller blades. IEEE Transactions on Magnetics, 33(2), 1432–1435.
[14] Jenn, D., & Ton, C. (2012). Wind turbine radar cross section. International journal of antennas and propagation, 2012.
Linkgyűjtemény
