Doctoral School of Electrical Engineering 

Department of Broadband Infocommunications and Electromagnetic Theory

Supervisor: Dr. Bilicz Sándor

Radar detection of unmanned aerial vehicles

Introducing the research area

Recently, Unmanned Aerial Vehicles (UAVs – drones) have been frequently used against both military and civilian targets, making their detection a high priority task [1]. Several methods of detection are being researched, including sonar [2], visual [3] and radar based methods [4]. The latter have several advantages, and have a long usage history in aviation control, however, classical radar methods can fail to detect some of the smaller sized drones due to their small Radar Cross Section (RCS -- a quantity of dimension m² describing the detectability of a target by radar). This is illustrated by the story of a drone, flown by an employee, performing an emergency landing in the garden of the White House without being detected by the automated defence systems of the presidential residence [5].

 

Brief introduction of the research place

My research was performed at the Electromagnetic Simulation and Design Laboratory, in collaboration with the Microwave Detection Laboratory at the Department of Broadband Infocommunications and Electromagnetic Theory.

 

History and context of the research

It is a well-known fact that a body performing a linear motion with a constant velocity when illuminated by an electromagnetic wave, will scatter a lower or higher frequency field depending on the direction of its motion – this is the so-called Doppler shift. When the motion of the body varies, e.g., it is periodic; it can result in several (possibly infinite) frequency components occurring in the scattered spectrum. This phenomenon is called the micro-Doppler effect.

 

The use of micro-Doppler phenomena for detecting small RCS planes is investigated in [6], including an experiment demonstrating additional frequency components in the spectrum of the field scattered from a small, rotating drone propeller manufactured of carbon fibre reinforced plastic. Although the size and RCS of a small drone’s propeller is even smaller than that of the whole plane, the discrete scattering spectrum characteristic for rotating motion makes it easier to distinguish from the environment, which can be used for locating the drone.

 

Fig. 1: Spectrum of the field scattered from a propeller with an accelerating rotation as a function of time. Note the frequency components differing from the carrier frequency, as well as the increasing shift with the increasing angular velocity of the propeller.

 

 

In the scientific literature, the interaction of electromagnetic radiation and bodies in periodic motion is usually investigated using frequency domain methods. Specifically, in radar applications, similar problems are investigated using physical optics models [7], however, for small propellers with lengths comparable to the wavelength, these methods are not applicable. In this case, it is necessary to solve the full system of Maxwell’s equations, taking into account the propeller’s rotation.

 

Research goals, open questions

Even before my arrival at the department, radar detection of UAVs was being investigated. The goal of my research was to create a mathematical model of scattering from a small, carbon fibre reinforced rotating propeller, and to validate theoretical results through anechoic chamber measurements.

 

The speed of calculation is of great importance. On the one hand, to allow an efficient integration of the rotating propellers into a model covering the whole UAV, and on the other hand, a larger number of function evaluations may be necessary during the application of quasi stationary approximation.

 

The anechoic chamber available at the department offered an excellent opportunity for the validation of the numerical results. The experiments were completed for multiple configurations; in addition to the more standard monostatic (transmitter and receiver antennas in the same position) setup, I wanted to examine the scattering in a bistatic (transmitter and receiver antennas in different positions) setup as well. The reason for the latter is that the frequency of the DVB-T broadcast is close to the resonant frequency of a typical sized (~ 25 cm) drone propeller, making detection by a passive radar possible.

The constructed models can be applied in active as well as passive radar systems; here, the goal will be the localization of the drone by recognizing and measuring the discrete spectral components in the scattered electromagnetic radiation.

 

Methods

The exact description of the interaction between a rotating scatterer and an incident electromagnetic wave is difficult, because the calculation of currents induced along the propeller – which generate the scattered field – requires the transformation of the EM field quantities into rotating reference systems. In most technical applications, however, being the velocity of the moving objects negligible with respect to the speed of light, one can use the quasi-stationary approximation [9], [10] to create a scheme which can accurately calculate the scattered field in two steps:

       - Expressing the scattered field of a stationary scatterer

       - Considering the effect of rotation through the use of the quasi-stationary approximation.

 

I investigated the field scattered from the stationary propeller with two methods: the finite element method [11] and the integral equation method [12].

 

Due to its general formulation and flexibility, the Finite Element Method (FEM) is often used in scattering and in diverse electromagnetic problems, however, the required computational capacity can be high due to the need for volume discretization, the unfavourable aspect ratio of the scatterer (for example, the length of a typical propeller is much larger than its width and thickness) and the need for discretizing the volume surrounding the scatterer. An additional advantage of this method is that it can be used to examine objects of practically all sizes and material properties.

 

Another possibility for modelling scattering from conductors is the Integral Equation (IE) based Method of Moments (MoM). The usage of MoM is advantageous from the perspective of computational capacity, because one dimensional – 1D – discretization is applicable; in our case, currents on the propeller are induced dominantly along its length (this can be verified through 3D simulations as can be seen in Fig. 2.). As a consequence, the number of Degrees of Freedom (DoF) is much smaller when compared to methods using volume discretization. Another advantage of the method is that discretization of the area surrounding the propeller in not required (in Fig. 3, we outline the FEM mesh of the propeller and its surroundings).

 

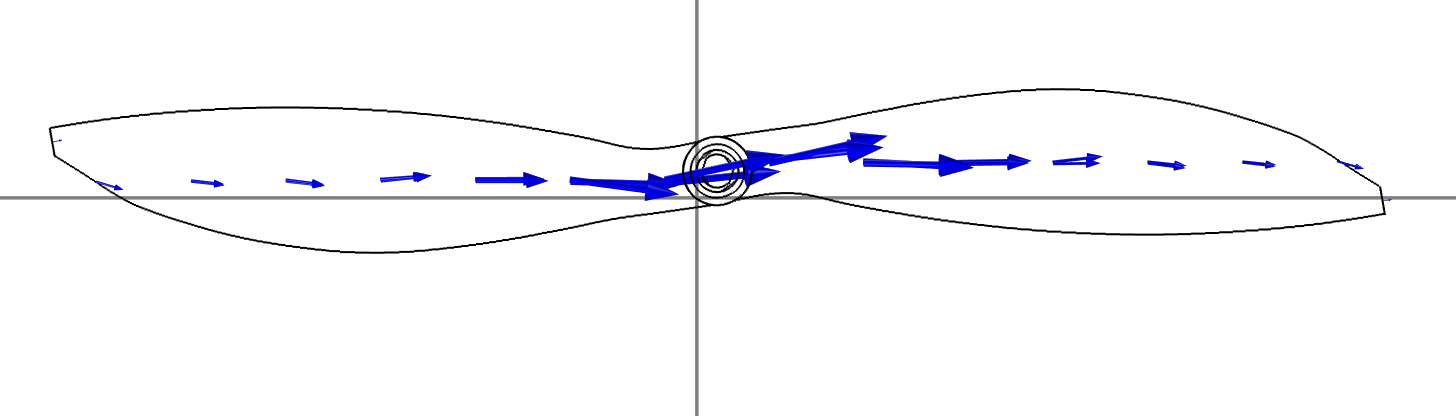
Fig. 2: Induced currents on a 10 inch propeller.

 

 

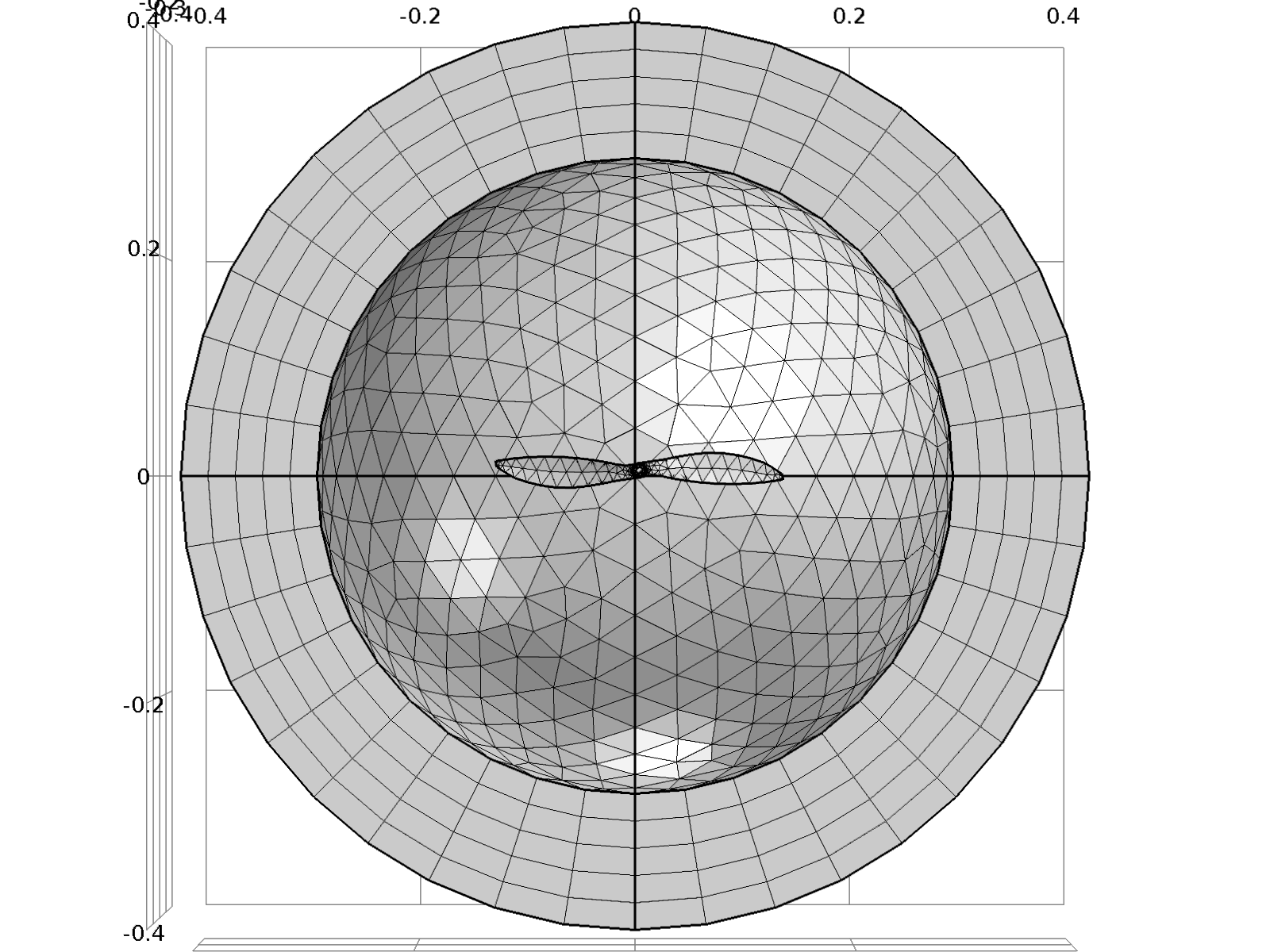
 Fig. 3: FEM mesh built for the scattering simulation, illustrating the need for the discretization of the propeller and its surroundings.

 

 

The downside of the scheme is that by default it uses boundary conditions corresponding to ideal conductors; although its use can be extended to materials with finite conductivity, further constraints introduced in this way will restrict the generality of the method. Based on the FEM calculations and measurements, however, these restrictions do not cause a significant error in radar detection scenarios, and the method can be used with good accuracy.

 

I created the FEM simulation models in the commercial software COMSOL, while the MoM scheme and the accompanying calculations were coded in Matlab.

The experiment was built in the aforementioned anechoic chamber (a sketch of the bistatic arrangement is included in Fig.4), and also on the top of building BME V1, so results both from free range as well as indoors measurements were available.

 

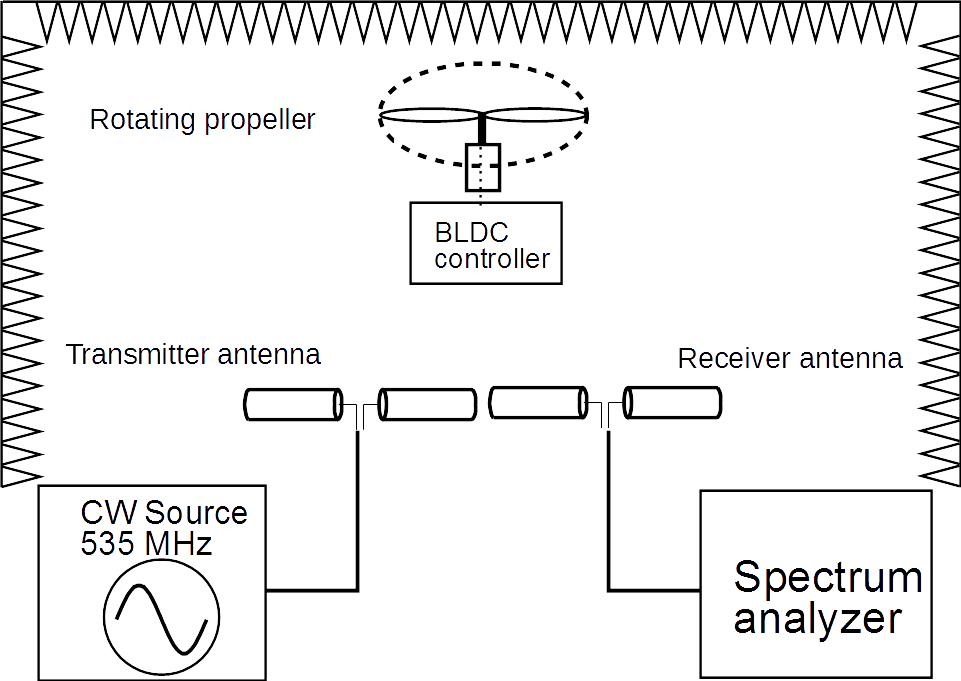
Fig. 4: Bistatic experimental arrangement.

 

Results

My first research goal was the theoretical description of scattering from rotating bodies. Although the RCS of rotating propellers and wind turbine propellers is investigated in the scientific literature ([13], [14]), the ray-tracing and physical optics models used herein are not applicable for smaller objects with dimensions close to the wavelength of the illuminating wave (such as the propeller investigated). Therefore, I devised a method which – combining the quasi-stationary method with an arbitrary numerical model – can calculate scattering spectrum of an object performing a periodic motion.

 

In the first step, simulation of the scattering was performed for several orientations of the propeller corresponding to the assumed positions during the rotation. Based on the results, the scattered field can be decomposed into a Fourier series in the angular variable describing the rotation. In my research, I have proven that the coefficients of the series are equal to the complex amplitudes in the discrete scattering spectrum. Having built the FEM model of the propeller, the scattered field could be easily calculated in any direction, making the model adequate for the description of monostatic and bistatic scenarios. Through careful examination of the results, I arrived at the conclusion that in addition to the ‘classical’ micro-Doppler effect (resulting from the movement of the scatterer towards or away from the observer), for objects whose dimensions are close to the wavelength, rotation in the plane perpendicular to the line connecting the observer and the scatterer also plays a role, as it can affect the currents induced on the scatterer.

 

Then, using the MoM, I created a 1D substitute model for the propeller, and proved that it is possible to choose the length and radius parameters to achieve equivalency (in terms of scattering) with the 3D model in a relatively broad frequency range (as shown in Fig. 5).

 

Fig. 5: Monostatic RCS of a 10 inch propeller as a function of frequency, calculated using FEM and MoM with appropriately chosen parameters.

 

 

Using the simpler 1D discretization, more complex scenarios can also be modelled efficiently. I created a model of two adjacent rotating propellers; in the scattered spectrum, the model predicts ‘mixed’ terms arising as a consequence of the propellers’ interaction.

 

For the purpose of validating the theoretical results, I performed anechoic chamber (Fig. 6) and free range scattering experiments. The measurement results confirm the theoretical predictions: we can observe a discrete spectrum (Fig. 7) with the measured peak intensities in good agreement with the numerical results. The dual propeller measurements are burdened with a greater error, however, qualitatively, the model predicts the character of the spectrum, as the expected mixed terms do indeed appear (Fig. 8).

 

Fig. 6: Bistatic experimental arrangement: the transmitting antenna (A_T) is on the right, the receiving antenna (A_R) is on the left, while the propeller (S) can be seen in the middle.

 

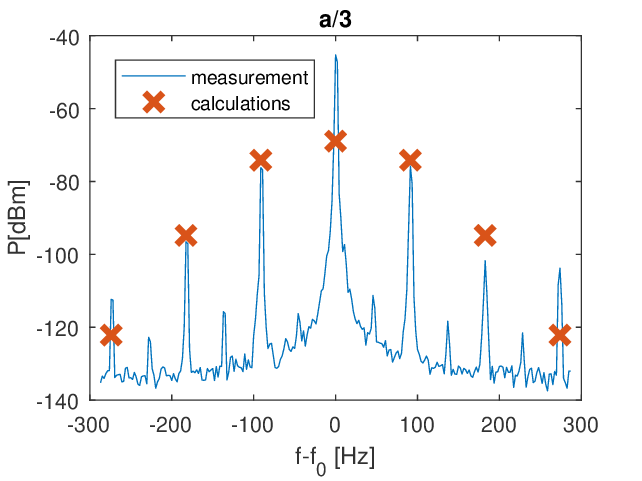
 Fig. 7: Experimental and numerical results of scattering from a propeller during a bistatic radar experiment. The calculations predict the intensity of the side peaks relatively accurately; the larger error at the carrier frequency is a result of miscellaneous scattering from the environment.

 

 

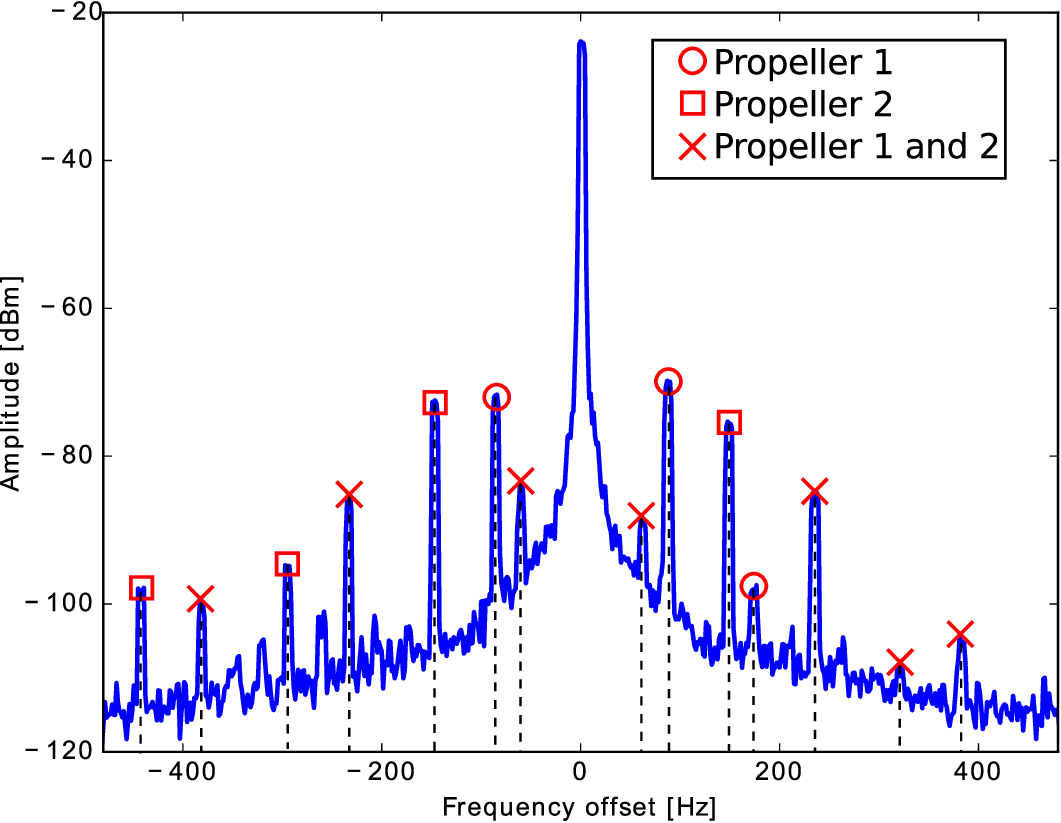
Fig. 8: Scattering spectrum of two adjacent rotating propellers 300 mm apart.

 

Expected impact and further research

The model describing scattering from small objects can find its applications in the detection of drones by radar, however, other possible applications include investigating the interference in automotive radars caused by fans in motorway tunnels. Since the resonant frequency of small drone propellers is close to the DVB-T band, the results (primarily concerning bistatic scenarios) presented may find applications in detections by passive radar systems.

 

During my work on drone propellers, I noticed that the material of the propeller plays a role in the computational model of the scattering, influencing the intensity of the scattered field, but also the resonant frequency of the propeller. Based on this observation, I designed an experimental setup making use of the micro-Doppler effect: if the field scattered from an elongated sample of known geometry, or the resonant frequency of the sample can be measured, we can draw conclusions as to the sample’s material. My results in the topic were published in [C5], [J3].

 

List of corresponding own publications

 

Journal articles

 

[J1] Marák, K., Pető, T., Bilicz, S., Gyimóthy, S., & Pávó, J. (2017). Electromagnetic simulation of rotating propeller blades for radar detection purposes. IEEE Transactions on Magnetics, 54(3), 1–4.

 

[J2] Marák, K., Pető, T., Bilicz, S., Gyimóthy, S., & Pávó, J. (2018). Bistatic RCS calculation for propellers at near-resonant frequencies. International Journal of Applied Electromagnetics and Mechanics, (Preprint), 1–8.

 

[J3] Marák, K. Experimental technique for high frequency conductivity measurement, accepted for publication. COMPEL—The International Journal for Computation and Mathematics in Electrical and Electronic Engineering.

 

Conference Articles

 

[C1] Marák, K. (2017). Calculation of the radar cross section of small propellers by means of an efficient integral equation method,” in Mesterpróba Proceedings, 20–23.

 

[C2] Marák, K., Pető, T., Bilicz, S., Gyimóthy, Sz. & Pávó, J. (2017). Electromagnetic simulation of rotating propeller blades for radar detection purposes. Proceedings of Compumag, Daejeon, 1–2.

 

[C3] Marák, K., Bilicz, S., Gyimóthy, Sz., Pávó, J. & Pető, T. (2017). Bistatic RCS calculation for propellers at near-resonant frequencies. Proceedings of ISEM -- International Symposium on Applied Electrodynamics and Mechanics, 1­–1.

 

[C4] Pető, T., Marák, K., Bilicz, S., & Pávó, J. (2018). Experimental and numerical studies on scattering from multiple propellers of small UAVs. Proceedings of EuCAP, 1–4.

 

[C5] Marák, K., Bilicz, S., & Pávó, J. (2018). Experimental technique for high frequency conductivity measurement,” Proceedings of IGTE Symposium, 1–1.

 

 

References

 

[1] Sturdivant, R. L., & Chong, E. K. (2017). Systems engineering baseline concept of a multispectral drone detection solution for airports. IEEE Access, 5, 7123–7138.

 

[2] Nijim, M., & Mantrawadi, N. (2016, May). Drone classification and identification system by phenome analysis using data mining techniques. In 2016 IEEE Symposium on Technologies for Homeland Security (HST) (pp. 1–5). IEEE.

 

[3] Rozantsev, A., Lepetit, V., & Fua, P. (2016). Detecting flying objects using a single moving camera. IEEE transactions on pattern analysis and machine intelligence, 39(5), 879–892.

 

[4] Drozdowicz, J., Wielgo, M., Samczynski, P., Kulpa, K., Krzonkalla, J., Mordzonek, M., ... & Jakielaszek, Z. (2016, May). 35 GHz FMCW drone detection system. In 2016 17th International Radar Symposium (IRS) (pp. 1–4). IEEE.

 

[5] https://www.nytimes.com/2015/01/27/us/white-house-drone.html, 2019.06.19

 

[6] Pető, T., Bilicz, S., Szűcs, L., Gyimóthy, S., & Pávó, J. (2016, April). The radar cross section of small propellers on unmanned aerial vehicles. In 2016 10th European Conference on Antennas and Propagation (EuCAP) (pp. 1–4). IEEE.

 

[7] Chen, V. C., Li, F., Ho, S. S., & Wechsler, H. (2006). Micro-Doppler effect in radar: phenomenon, model, and simulation study. IEEE Transactions on Aerospace and electronic systems, 42(1), 2–21.

 

 

[8] Daun, M., Nickel, U., & Koch, W. (2012). Tracking in multistatic passive radar systems using DAB/DVB-T illumination. Signal Processing, 92(6), 1365–1386.

 

[9] Cooper, J., & Wilcox, C. H. (1980). Scattering by moving bodies: the quasi stationary approximation. Mathematical Methods in the Applied Sciences, 2(2), 131–148.

 

[10] Van Bladel, J. (2012). Relativity and engineering (Vol. 15). Springer Science & Business Media.

 

[11] Jin, J. M. (2015). The finite element method in electromagnetics. John Wiley & Sons.

 

[12] Gibson, W. C. (2007). The method of moments in electromagnetics. Chapman and Hall/CRC.

 

[13] Yang, S. Y., Yeh, S. M., Bor, S. S., Huang, S. R., & Hwang, C. C. (1997). Electromagnetic backscattering from aircraft propeller blades. IEEE Transactions on Magnetics, 33(2), 1432–1435.

 

[14] Jenn, D., & Ton, C. (2012). Wind turbine radar cross section. International journal of antennas and propagation, 2012.

 

Links

 

BME HVT

 

HVT anechoic chamber

 

Passive radar wikipedia  

 

COMSOL

 

Matlab