|
|
BMe Kutatói pályázat |
|
Oláh György Doktori Iskola
BME Vegyészmérnöki és Biomérnöki Kar, Fizikai Kémia és Anyagtudományi Tanszék
Témavezető: Dr. Kállay Mihály
Többszintű kvantumkémiai módszerek fejlesztése
A kutatási téma néhány soros bemutatása
A molekuláris tulajdonságok megbízható előrejelzésére képes hagyományos kvantumkémiai módszereket legfeljebb egy tucat atomból álló rendszereken tudunk rutinszerűen alkalmazni. Ennek a problémának a megoldására egy olyan eljárást mutatok be pályázatomban, amely ötvözi az 1998-as [1] és 2013-as [2] kémiai Nobel-díjazottak munkásságát csoportunk lokális közelítéseken alapuló elektronkorrelációs technikájával [3]. Ezáltal a pontos számítások minden eddiginél hatékonyabban végezhetőek el akár több tízezer atomra is [M1, M2, M3].
A kutatóhely rövid bemutatása
Munkámat a BME Fizikai Kémia és Anyagtudományi Tanszéken végeztem dr. Kállay Mihály egyetemi tanár vezetésével. Csoportunk fő kutatási profilja az új kvantumkémiai módszerek fejlesztése és hatékony programozása. Az új algoritmusok a csoportvezető által létrehozott MRCC nevű kvantumkémiai programcsomagban [4] valósulnak meg, amelynek több száz aktív felhasználója van. A csoport nemzetközi mércével is rendkívül eredményes, és a munkát olyan neves pályázatok is támogatták mint az ERC starting grant, Lendület, Élvonal – Kutatói Kiválósági programok.
A kutatás történetének, tágabb kontextusának bemutatása
Paul Dirac, angol fizikus szerint a teljes kémiát leíró fizikai törvényeket már ismerjük és az egyetlen nehézség, hogy ezek a törvények olyan bonyolult egyenletekhez vezetnek, amelyeket nem tudunk egzaktul megoldani [5]. A modern számításos kémia így a Schrödinger-egyenlet közelítő megoldásán alapszik: a hullámfüggvény-elmélet (wavefunction theory, WFT), amely egy sor ismert közelítést tesz a rendszert jellemző hullámfüggvényen, 1 kcal/mol pontossággal képes [6] modellezni egy tucat atomot, ami a termokémiai kísérletek tipikus pontossága. A WFT-módszerek szimulációs ideje azonban a rendszer méretének nagyfokú hatványával arányos, így ezt a technikákat a jövőben az egyre növekvő számítástechnikai kapacitások mellett is csak korlátozottan lehet majd használni.
Az évek során a tudósok nagy erőfeszítéseket tettek annak érdekében, hogy nagyobb rendszereket is lehessen modellezni. A sűrűségfunkcionál-elmélet (density functional theory, DFT) Kohn-Sham-modellje empirikus paraméterekkel egészítette ki a függetlenrészecske-modellt, amivel akár 1000 atomos rendszereket is számolhatunk. A kvantumkémia kombinálása a klasszikus mechanikán alapuló, ám jóval kevesebb paramétert igénylő molekulamechanikával (MM) lehetővé tette a nanorészecskék szimulációját is. Mindkét megközelítést forradalmi újításnak ítélte meg a tudományos közösség, amit Nobel-díjjal jutalmaztak [1,2], de további fejlesztésekre van szükség, mivel az olyan fejlődő területek, mint a számítógépes gyógyszertervezés egyre pontosabb és hatékonyabb módszereket igényelnek.
A kutatás célja, a megválaszolandó kérdések
A kezdeti 1990-es évekhez képest sokat fejlődött a DFT, de a bonyolultabb módszerek egyre több szimulációs időt igényelnek, és továbbra sincs garantálva a pontosságjavulás az alkalmazott empirikus paraméterek miatt, így kvalitatíve rossz predikciók veszélye is fennállhat [7] (pl. reakcióutak feltérképezésekor). Bár a pontosságért kapott hatékonyság nagyon előnyös, a nagymolekulák modellezése még mindig nem lehetséges, vagy rendkívül időigényes.
Lokalizált reakciók esetén, a QM-módszerek skálázódásának problémája kikerülhető a QM/MM technikával, amelyben a QM és MM módszereket együtt használjuk [8]. Enzimreakcióknál például a rendszernek csak egy kis részében lesz jelentős elektronszerkezet-változás (aktív rész), míg környezetének elektronsűrűsége gyakorlatilag változatlan marad (lásd 1. ábra). Ebből logikusan következik, hogy csak a változásban érintett részt érdemes pontos, de időigényes kvantumkémiai módszerrel leírni, míg annak környezetét hatékony molekulamechanikával vesszük figyelembe. Bár a QM/MM technikával már a nanoméretű anyagok is modellezhetők, újabban kimutatták, hogy viszonylag nagy, legalább 500-600 atomos QM részre van szükség pontos számításokhoz [9].
Ezek alapján a kutatásunk legfőbb célja, hogy növeljük a QM-régió számításának hatékonyságát pontosságvesztés nélkül. Javaslatot teszek egy olyan kombinált, többszintű módszer megalkotására, ami egyesíti a WFT-, DFT- és MM-módszerek előnyeit, valamint azt is bemutatom, hogyan érdemes a különbözőképpen kezelt régiókat megválasztani.
Módszerek
WFT- és DFT-módszerek kombinálása: WFT-in-DFT
A QM/MM során alkalmazott felosztási elvet a WFT- és DFT-módszereknél is felhasználhatjuk. Két kvantumalapú módszer naiv együttes használata azonban átfedő molekulapályákhoz vezet, ami rossz közelítése a hullámfüggvényének. Az általunk alkalmazott eljárásnak a lényege, hogy először a teljes rendszerre alkalmazunk valamilyen DFT-módszert, majd az érdekes aktív részen lokalizált pályákat úgy használjuk fel WFT-számításhoz, hogy közben a környezet pályáit projekció segítségével változatlanul hagyjuk [10,M2].
WFT-technika lokális közelítésekkel: WFT-in-WFT
A csoportunkban fejlesztett elekronkorrelációs technika [3] alapja, hogy a részecskék közötti kölcsönhatás a köztük lévő távolság hatodik hatványával csökken. Ha a teljes rendszerre kiterjedt kanonikus molekulapályákat valamilyen kémiai szemléleten alapuló algoritmus szerint lokalizáljuk, akkor a közeli, erős elekron-kölcsönhatásokat pontos, míg a távoliakat durva közelítéssel írhatjuk le. Tekintve, hogy így minden kölcsönhatáshoz hozzárendelünk távolságfüggő közelítéseket, egyszerűen definiálhatunk egy többszintes technikát, ahol csak az aktív részen lokalizálódott molekulapályák esetén számítjuk ki az erős kölcsönhatásokat pontos módszerrel. A környezet pályáinál a közeli kölcsönhatásokra is csak a közelítő eljárást alkalmazzuk [M2].
Duális-kevert báziskészlet
A kvantumkémiai számításokban általában atomokon centrált Gauss-függvényekkel közelítjük az atompályákat, amelyek lineáris kombinációjából tevődnek össze a molekulapályák (LCAO-MO-közelítés). A Gauss-függvények használata számítástechnikailag rendkívül előnyös a számításokban, azonban nem jól közelítik az atompályákat, így pontos számításokhoz viszonylag sok Gauss-függvényre van szükségünk (más függvényekkel szemben így is megéri). Logikusan adódhat az ún. kevertbázis-közelítés, amelynél az aktív rész atomjain több, míg környezet atomjain kevesebb Gauss-függvényt alkalmazunk a számításokban. Ez egy rendkívül egyszerű eljárás, de mesterségesen polarizálhatja a hullámfüggvényt, ami nagy hibákhoz vezethet. Head-Gordon és munkatársai technikáját [11] továbbfejlesztve egy olyan duális-kevertbázis-közelítést javasoltunk [M3]. Ennek lényege, hogy a hullámfüggvény optimálásánál minden atomra nézve kevés Gauss-függvényt alkalmazunk (ezt kis báziskészletnek hívjuk), de a végső, optimált hullámfüggvényen egy elsőrendű korrekciót alkalmazunk a kevert bázissal.
Eddigi eredmények
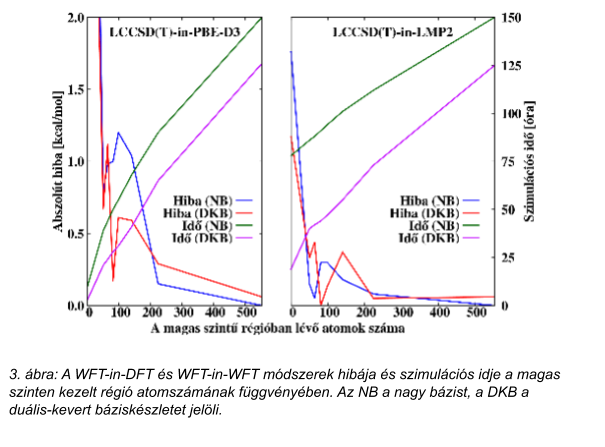
A továbbiakban egy háromdimenziós, valós példán fogom bemutatni, hogy mekkora hatékonyságjavulás várható a pontosság csökkenésért cserébe, ha a többrétegű kvantumalapú módszereket QM/MM-el kombináljuk. Ez a rendszer a biológiai jelentőséggel bíró Catechol-O-Methyltransferase (COMT) enzim, amelynek fontos szerepe van a neurotranszmitter regulációban azáltal, hogy egy metilcsoport átadását katalizálja az S-adenosyl-L-methionine-ről (SAM) deprotonált, katekol-alapvázú (CAT) molekulákra. Referenciamódszernek tekintsünk egy olyan QM/MM számolást, ahol a QM-alrendszer kellően nagy (lásd 1. ábra), és ahol a QM-alrendszeren egy lokális közelítéseket alkalmazó, magas szintű WFT-módszert használunk (lokális csatolt klaszter (coupled-cluster) módszer egyszeres, kétszeres és közelítő háromszoros gerjesztésekkel, LCCSD(T)). A többszintű módszerekkel számított reakcióenergiák hibáját a következőekben a magas szinten kezelt atomok számának függvényében fogom bemutatni, így a QM-régiót 6 további alrendszerre osztottam, amelyben az aktív régió mérete fokozatosan növekszik (lásd 2. ábra).
A 3. ábrán azt láthatjuk, hogy miként változik a többszintes módszerünk hibája, ha a magas szintű WFT módszert egy DFT- [12] (korrigált Perdew-Burke-Ernzerhof funkcionál, PBE-D3) vagy egy alacsonyabb-szintű WFT-módszerrel (másodrendű Møller-Plesset lokális közelítéssekkel, LMP2) együtt használjuk. Mindkét módszernél láthatjuk, hogy viszonylag sok, 100–200 atom szükséges a magas szintű régióba ahhoz, hogy a hiba a referenciamódszer hibájánál – amely kb. 1 kcal/mol – jóval kisebb legyen. A WFT-in-WFT pontosabb közelítésnek mutatkozik, mint a WFT-in-DFT, de az utóbbi akár 1 nagyságrendnyi gyorsulást is eredményezhet, ha nagyobb hibát engedünk meg. A duális-kevertbázis eredményei kapcsán láthatjuk, hogy a használatával a számítás hibája hasonló nagyságú, mint a tisztán nagy báziskészlet használatakor, de jelentős, 15–30%-os gyorsulást is eredményezhet.
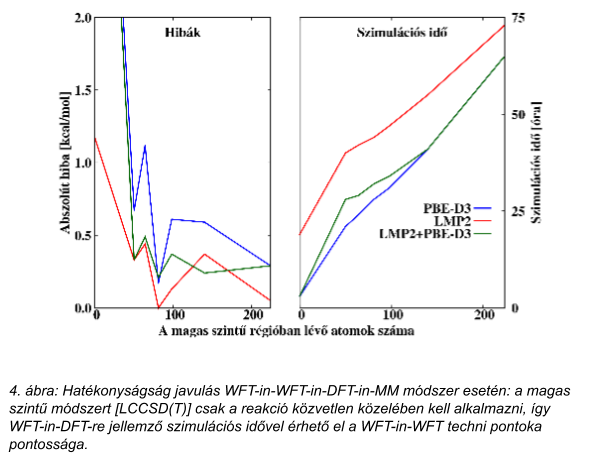
Végezetül azt is láthatjuk a 6. ábrán, hogy a pontos és hatékony WFT-in-DFT-módszert tovább gyorsíthatjuk, ha csak a legfontosabb molekulapályákat kezeljük magas szinten, és egy köztes, alacsonyabb-szintű WFT-részt alkalmazunk a magas szintű WFT-és DFT-technikák között. A legjobban teljesítő WFT-in-WFT-in-DFT-in-MM-módszerrel a magas szintű módszert néhány tized kcal/mol pontossággal közelítő eredményeket kaphatunk egyetlen számítógép kb. egy napos használatával [M3].
Várható impakt, további kutatás
A bemutatott fejlesztések már most is alkalmazhatóak a molekulamechanikai AMBER és az MRCC programcsomagok együttes alkalmazásával [M1]. Mindkét program ingyenesen hozzáférhető akadémiai célokra. A többszintű módszerek hatékony és megbízható referenciamódszerek lehetnek közelítő módszerek validálásakor, de akár pontos eljárásokként is használhatóak energiakülönbségek (reakcióenergiák, reakciógátak) számítására.
A többszintes módszernek azonban súlyos hátulütője, hogy csak energiaszámításra alkalmas. Más molekuláris tulajdonságok, mint az atomokon fellépő erők, amelyek nélkülözhetetlenek pl. reakcióutak feltérképezéséhez, meghatározása nem hatékony, ezért az algoritmus további fejlesztésekre szorul. Jelenlegi kutatásaink alapján azonban már ezt a problémát is sikerült megoldani [M4], így várakozásaink szerint a jövőben bemutatandó módszerünk széles körben fog elterjedni.
Saját publikációk, hivatkozások, linkgyűjtemény
Kapcsolódó saját publikációk listája
[M1] B. Hégely, F. Bogár, G. G. Ferenczy, M. Kállay, Theor. Chem. Acc., 2015, 134, 132 (IF=1.806)
[M2] B. Hégely, P. R. Nagy, G. G. Ferenczy, M. Kállay, J. Chem. Phys. 2016, 145, 064107 (IF=2.965)
[M3] B. Hégely, P. R. Nagy, M. Kállay, J. Chem. Theory Comput., 2018, 14, 4600 (IF=5.313)
[M4] B. Hégely, M. Kállay, készülőben.
További publikációk
[M4] D. Hessz, B. Hégely, M. Kállay, T. Vidóczy, M. Kubinyi, J. Phys. Chem. A, 2014, 118, 28 (IF=2.693)
[M5] B. Kirschweng, K. Bencze, Sárközi, B. Hégely, G. Samu, J. Hári, D. Tátraaljai E. Földes, M. Kállay and B. Pukánszky, Polym. Degrad. Stabil., 2016, 133, 192 (IF=2.08)
[M6] B. Kirschweng, D. M. Tilinger, B. Hégely, G. Samu, D. Tátraaljai, E. Földes, B. Pukánszky, Eur. Polym. J., 2018, 103, 228 (IF=3.621)
Linkgyűjtemény
Møller–Plesset perturbáció-elmélet
Hivatkozások listája
[1] The Nobel Prize in Chemistry 1998. Nobelprize.org. Nobel Media AB 2014. Web. 3 Aug. 2018. https://www.nobelprize.org/prizes/chemistry/1998/summary/
[2] The Nobel Prize in Chemistry 2013. Nobelprize.org. Nobel Media AB 2014. Web. 3 Aug. 2018. https://www.nobelprize.org/prizes/chemistry/2013/summary/
[3] P. R. Nagy, G. Samu, M. Kállay, J. Chem. Theory. Comput. 2018, 14, 4193
[4] Mrcc, a quantum chemical program suite written by M. Kállay, Z. Rolik, J. Csontos, P. Nagy, G. Samu, D. Mester, J. Csóka, B. Szabó, I. Ladjánszki, L. Szegedy, B. Ladóczki, K. Petrov, M. Farkas, P. D. Mezei, and B. Hégely.
[5] P. A. M. Dirac, Proc. R. Soc. Lond. A, 1929, 123, 714
[6] A. Ganyecz, M. Kállay, J. Csontos, J. Chem. Theory Comput., 2017, 13, 4193
[7] M. W. van der Kamp, J. Zurek, F. R. Manby, J. N. Harvey, A. J. Mulholland, J. Phys. Chem. B, 2010, 114, 11303
[8] A. Warshel, M. Levitt, J. Mol. Biol., 1976, 103, 227
[9] H. J. Kulik, J. Zhang, J. P. Klinman, T. J. Martínez, J. Phys. Chem. B., 2016, 120, 11381
[10] F. R. Manby, M. Stella, J. D. Goodpaster and T. F. Miller III, J. Chem. Theory Comput., 2012, 8, 2564
[11] W. Liang, M. Head-Gordon, J. Phys. Chem. A., 2004, 108, 3206
[12] J. P. Perdew, K. Burke, M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865