|
|
BMe Research Grant |
|
George A. Olah Doctoral School of Chemistry and Chemical Technology
Department of Physical Chemistry and Materials Science
Supervisor: Dr. Kállay Mihály
The Development of Multilevel Quantum Chemistry Methods
Introducing the research area
Those traditional quantum chemistry methods which can produce reliable predictions for molecular properties can only be used on molecules of a dozen atoms routinely. In this application, I will present a procedure which merges our local approximation-based electron correlation technique [3] with the works that are acknowledged with the Nobel Prizes in Chemistry in 1998 [1] and in 2013 [2]. Thus accurate simulations can be carried out more efficiently than ever before on a few tens of thousands atoms [M1,M2,M3].
Brief introduction of the research place
My research is carried out at the Department of Physical Chemistry and Materials Science, BUTE, under the supervision of Professor Mihály Kállay. The development and efficient implementation of new quantum chemistry methods is the main focus of the research group. These new algorithms are implemented in the MRCC quantum chemistry program package [4], which is established by Prof. Kállay and has a few hundred active users. The group can be considered highly successful by international standards, and the work was supported by notable grants, such as ERC starting grant, Lendület, Élvonal – Kutatói Kiválósági program.
History and context of the research
According to the English physicist Paul Dirac, the laws which describe the whole of chemistry are completely known and the only difficulty is that these laws lead to too complicated equations that cannot be solved exactly [5]. Thus, the modern computational chemistry is based on the approximate solution of the Schrödinger equation: wave function theory (WFT), which introduces a series of known approximations on the wave function of the system, is capable of modeling a couple of dozens of atoms with 1 kcal/mol accuracy [6], which is the typical accuracy of thermochemical experiments. However, the simulation time of these approaches scales as a high power with the system size thus their application will also be limited in the future despite the ever-growing computational capacities.
Numerous efforts have been made over the years to expand the application range. The Kohn–Sham model of density functional theory (DFT), where empirical parameters are introduced into the independent particle model, allowed the simulated systems to be up to 1000 atoms large. The combination of quantum chemistry with molecular mechanics (MM), which requires much fewer parameters and it is based on classical mechanics, enabled the simulation of nanoparticles. Both approaches were groundbreaking developments, which were rewarded in the forms of Nobel-prizes [1,2] by the scientific community, but further developments are required because emerging fields, for instance, computer-aided drug design, demand more accurate and more efficient methods.
The research goals, open questions
DFT developed a lot since the early 1990s, but the more complicated methods require more simulation time, and the improvement of accuracy is not guaranteed because of the used empirical parameters, thus there is a risk of wrong qualitative results [7], for example, in the case of reaction route mapping. Its efficiency is very advantageous; however, the simulation of large molecules is still not possible or very time consuming.
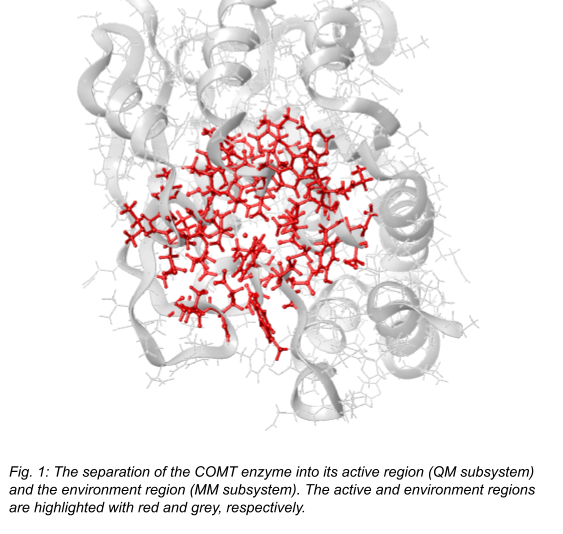
In the case of localized reactions, the scaling-problem of the QM methods can be bypassed by the QM/MM method, where QM and MM methods are used together [8]. For example, in the case of enzyme reactions, the significant change in electron density is limited to a small portion of the whole system (the active site), while the density of the environment is practically unchanged (see Fig. 1). Thus, quantum chemical methods, which can be highly accurate but time consuming, can be used on the active site, while the more efficient molecular mechanics can handle the environment. Although the use of QM/MM enables the simulation of nanoparticles, recent studies pointed out that a relatively large QM subsystem, which contains about 500-600 atoms, is necessary for accurate calculations [9].
In the light of these findings, our main goal is to increase the efficiency of the QM subsystem calculations without losing accuracy. I will propose a combined, multilevel technique, which unifies the advantageous properties of WFT, DFT, and MM methods, and I will also show how to select the differently handled regions.
Methods
Combining the WFT and DFT methods: WFT-in-DFT
The partitioning strategy of QM/MM can be also used in the context of WFT and DFT methods. However, the naive combination of the two quantum-based techniques leads to overlapping molecular orbitals, which is a wrong approximation of the wave function. The essence of our procedure is that the whole system is first treated with a DFT technique, and then the molecular orbitals, which are localized on the active region, will be handled by the WFT method so that the orbitals of the environment will be kept unchanged using a projection [10, M2].
WFT approach with local approximations: WFT-in-WFT
The electron correlation technique developed by our team [3] utilizes the decrease of interaction between the particles with the sixth power of the distance between them. If the canonical molecular orbitals, which are delocalized on the whole system, are localized on the basis of chemist's intuition, one can describe close interactions with an accurate method, while distant interactions can be treated in a more approximate way. Considering that distance-based approximations are assigned to every interactions, one can easily define a simple multilevel technique, where strong interactions are only calculated with the accurate method at orbitals localized on the active subsystem. For the orbitals of the environment, an approximate technique is used for both close and distant interactions [M2].
Dual-mixed basis set
Gaussian functions centered on atoms are usually used in quantum chemistry to approximate atomic orbitals, which are linearly combined to describe molecular orbitals (LCAO-MO approximation). Although the application of Gaussians is advantageous from the computational standpoint, they are not good approximations for the atomic orbitals, thus relatively large amount of Gaussians are required (yet in contrast with other functions, it still pays off). Thus, it is logical to define a mixed-basis set, where we use more Gaussians on the atoms of the active site and employ fewer functions on the atoms of the environment. This approach is very simple, but it can artificially polarize the wave function and can lead to significant errors. Based on the work of Head-Gordon and co-workers [11], we introduced a dual-mixed basis set [M3]. The essence of this approach is that we use fewer Gaussians on all atoms (this is called the small basis set) during the optimization of the wave function and apply a first-order correction on the final, optimized wave function with the mixed-basis set.
Results
The following three-dimensional realistic example will demonstrate the efficiency gain obtained in exchange for the loss of accuracy if we combine the described techniques with QM/MM. The test system will be the biologically relevant Catechol-O-Methyltransferase (COMT) enzyme, which has an important role in the neurotransmitter regulation by catalyzing a methyl group transfer from the S-adenosyl-L-methionine (SAM) to the deprotonated, catechol-based (CAT) molecules. As a reference method, we chose a QM/MM calculation, where the QM subsystem is sufficiently large (see Fig. 1), and the QM subsystem is treated with a high-level WFT method with local approximations (a local coupled-cluster technique with single, double and approximate triple excitations, LCCSD(T)). The error in reaction energies computed with multilevel methods will be shown as a function of the number of atoms treated with high-level techniques. Thus, the QM subsystem is separated into 6 QM subsystems, which are gradually increased and depicted in Fig. 2.
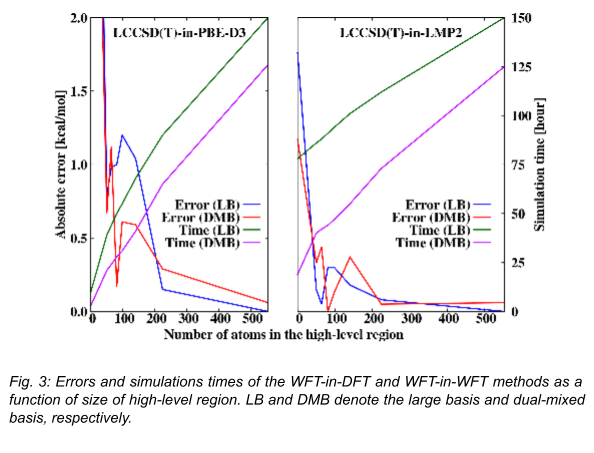
In Fig. 3, it can be seen how the error of the multilevel method changes when high-level method is used with a DFT [12] (using a corrected Perdew-Burke-Ernzerhof functional, PBE-D3) or low-level WFT (second-order Møller-Plesset with local approximations, LMP2) technique. We can see that both approaches require a relatively large number of atoms, 100-200 in the high-level region to reduce the error of the multilevel scheme below of the error of the reference method, which is approximately 1 kcal/mol. The WFT-in-WFT approach can be seen as a more accurate method compared to WFT-in-DFT but the latter is capable of increasing the efficiency by an order of magnitude, if we tolerate larger errors. The results from the dual-mixed basis set calculations demonstrate that the errors obtained with this approach are similar to those received with the large basis sets, and a significant, 15-30% performance (speed) improvement can be archived.
Finally, Fig 4 shows that the accurate and efficient WFT-in-DFT method can be further improved if we apply the high-level method only on the most important molecular orbitals, i.e. an intermediate low-level WFT method is introduced between the WFT and DFT methods. The best performing WFT-in-WFT-in-DFT-in-MM technique can approximate the accuracy of high-level techniques within a couple of tenths of kcal/mol as the simulation time is about one day in the case of a single computer [M3].
Expected impact and further research
The presented developments are ready for use with the molecular mechanics program AMBER and the quantum mechanics program MRCC [M1]. Both programs are free to use for academic purposes. These techniques can be used to calculate energy differences accurately (for example, reaction barriers) and they can also serve as efficient and reliable reference methods for the validation of more approximate methods.
A serious deficiency of these methods is the inefficient determination of other molecular properties, for example, the atomic forces, which are essential for reaction route mapping. Thus, the algorithm have to be further refined. We already addressed this problem in the case of WFT-in-DFT [M4], thus we expect the widespread use of the method in the future.
Publications, references, links
List of relevant publications
[M1] B. Hégely, F. Bogár, G. G. Ferenczy, M. Kállay, Theor. Chem. Acc., 2015, 134, 132 (IF=1.806)
[M2] B. Hégely, P. R. Nagy, G. G. Ferenczy, M. Kállay, J. Chem. Phys. 2016, 145, 064107 (IF=2.965)
[M3] B. Hégely, P. R. Nagy, M. Kállay, J. Chem. Theory Comput., 2018, 14, 4600 (IF=5.313)
[M4] B. Hégely, M. Kállay, in preparation
List of further publications
[M4] D. Hessz, B. Hégely, M. Kállay, T. Vidóczy, M. Kubinyi, J. Phys. Chem. A, 2014, 118, 28 (IF=2.693)
[M5] B. Kirschweng, K. Bencze, Sárközi, B. Hégely, G. Samu, J. Hári, D. Tátraaljai E. Földes, M. Kállay and B. Pukánszky, Polym. Degrad. Stabil., 2016, 133, 192 (IF=2.08)
[M6] B. Kirschweng, D. M. Tilinger, B. Hégely, G. Samu, D. Tátraaljai, E. Földes, B. Pukánszky, Eur. Polym. J., 2018, 103, 228 (IF=3.621)
Table of links
https://en.wikipedia.org/wiki/Schr%C3%B6dinger_equation
Møller–Plesset perturbation theory
List of references
[1] The Nobel Prize in Chemistry 1998. Nobelprize.org. Nobel Media AB 2014. Web. 3 Aug 2018. https://www.nobelprize.org/prizes/chemistry/1998/summary/
[2] The Nobel Prize in Chemistry 2013. Nobelprize.org. Nobel Media AB 2014. Web. 3 Aug 2018. https://www.nobelprize.org/prizes/chemistry/2013/summary/
[3] P. R. Nagy, G. Samu, M. Kállay, J. Chem. Theory. Comput. 2018, 14, 4193
[4] Mrcc, a quantum chemical program suite written by M. Kállay, Z. Rolik, J. Csontos, P. Nagy, G. Samu, D. Mester, J. Csóka, B. Szabó, I. Ladjánszki, L. Szegedy, B. Ladóczki, K. Petrov, M. Farkas, P. D. Mezei, and B. Hégely
[5] P. A. M. Dirac, Proc. R. Soc. Lond. A, 1929, 123, 714
[6] A. Ganyecz, M. Kállay, J. Csontos, J. Chem. Theory Comput., 2017, 13, 4193
[7] M. W. van der Kamp, J. Zurek, F. R. Manby, J. N. Harvey, A. J. Mulholland, J. Phys. Chem. B, 2010, 114, 11303
[8] A. Warshel, M. Levitt, J. Mol. Biol., 1976, 103, 227
[9] H. J. Kulik, J. Zhang, J. P. Klinman, T. J. Martínez, J. Phys. Chem. B., 2016, 120, 11381
[10] F. R. Manby, M. Stella, J. D. Goodpaster and T. F. Miller III, J. Chem. Theory Comput., 2012, 8, 2564
[11] W. Liang, M. Head-Gordon, J. Phys. Chem. A., 2004, 108, 3206
[12] J. P. Perdew, K. Burke, M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865