Vásárhelyi Pál Építőmérnöki és Földtudományok Doktori Iskola 

MTA-BME Vízgazdálkodási Kutatócsoport

Témavezető: Dr. Baranya Sándor

Vegyes szemösszetételű folyómedrek numerikus morfodinamikai modellezésének módszertani fejlesztése

A kutatási téma néhány soros bemutatása

A vízfolyások medrének geometriája és mederanyaga térben és időben is jelentős változásokon mehet keresztül. Ezen folyamatokat elsősorban a változatos áramlási kép gerjeszti. A megváltozott medergeometria és szemösszetétel viszont visszahat az áramlási képre. A morfodinamika tudománya az áramlás és a mederváltozás közötti kapcsolatot kutatja. Fő célja a jelen folyamatok feltárása mellett a várható mederváltozások előrejelzése.

Mivel számos emberi tevékenység (mezőgazdaság, halászat, hajózás, rekreációs tevékenységek) és természetes jelenség (növény és állatvilág élőhelye) áll közvetlen kapcsolatban a vízfolyások morfodinamikai állapotával, az áramlási és medergeometriai viszonyok megbízható előrejelzésére jelentős igény mutatkozik.

A kutatóhely rövid bemutatása

A Vízgazdálkodási Kutatócsoport egy hangsúlyos kutatási témája a hazai Duna morfodinamikai sajátosságainak vizsgálata és numerikus modellezésének fejlesztése. A rendelkezésre álló fejlett eszközpark lehetővé teszi magas színvonalú terepi mérések elvégzését, valamint a kutatócsoport numerikus modellezés terén is nemzetközileg elismert eredményeket sorakoztat fel. A kutatócsoport 7. éve űzi morfodinamikai kutatási tevékenységét Dr. Józsa János vezetésével, nemzetközileg is elismert eredményeket felmutatva.

A kutatás történetének, tágabb kontextusának bemutatása

A folyómedrek medergeometria-változásának vizsgálata a XX. században kezdődött. A fő cél olyan eljárások kidolgozása volt, amellyel meg lehet becsülni a várható mederváltozásokat. Kezdetben laboratóriumi kísérletek alapján próbáltak olyan empirikus összefüggéseket (hordaléktranszport-modellek) felállítani, amelyek a valóságban csak nagyon ritkán előforduló, kevésbé összetett körülmények esetén alkalmazhatók [1], [2]. A mérések az egyszerűbben meghatározható áramlási jellemzők (pl. áramlási sebesség, v; vízmélység, h) és hordalékjellemzők (jellemző szemcseméret, d; hordalékhozam, q_bi) mérésére terjedtek ki, a kapcsolatokat leíró empíriák felállítása céljából. Az így kidolgozott hordaléktranszport-modellek alkalmazhatósága tehát korlátozott; összetett medergeometriájú, vegyes szemösszetételű, valamint térben és időben is változatos morfodinamikai paraméterekkel jellemezhető folyómedrek mederváltozásának megbízható számítására azok nem nyújtanak alternatívát. Később, az áramlásmodellezés és az egyre nagyobb számítási kapacitással bíró informatikai háttér fejlődésével lehetőség nyílt olyan számítási igényű folyamatok számítására, mint pl. hosszabb folyószakaszok mederváltozásának becslése [3], [4], [T1], [T2].

 

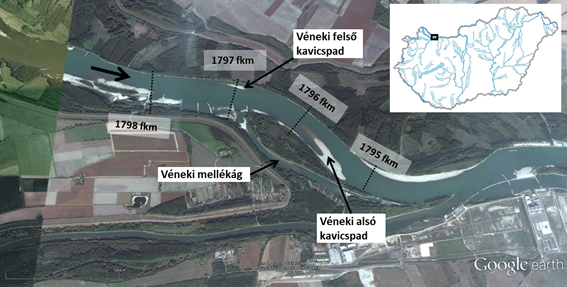
1. ábra: A Duna 1794 fkm – 1799 fkm közötti szakasza

 

A fejlett számítástechnikai infrastruktúra ellenére összetett morfodinamikájú folyószakaszok numerikus modellezésének megbízhatóságát még napjainkban is jelentősen csökkentik a hordaléktranszport-modellek alkalmazhatósági korlátai. Így például, a van Rijn [5] által kidolgozott modell csak a homokfrakció transzportjának leírására használható, míg a Wilcock és Crowe-modell [6] csak abban az esetben alkalmazható, amikor a kavics transzportja dominál. Olyan összetett morfodinamikai folyamatokat megbízhatóan leíró hordaléktranszport-modell azonban még mindig nem található a szakirodalomban, amely térben és időben is változatos mederanyag-szemösszetételt (tipikusan pl. középszakasz-jellegű folyószakaszok esetén) megbízhatóan tudna számítani. A hordaléktranszport-modellek fejlesztése területén ez a problémakör egy mai napig meg nem oldott feladatot kínál a kutatók számára.

A kutatás célja, a megválaszolandó kérdések

A hazai Felső-Duna középszakasz jellege révén meanderező vonalvezetésű, valamint vegyes szemösszetétellel jellemezhető. A természetes adottságokon túl az elmúlt évtizedekben létesített műtárgyak beépítése (sarkantyúk, partvédőművek, Bősi-erőmű) tovább fokozta az egyébként is összetettnek mondható morfodinamikai folyamatokat. Vagyis térben és időben is változatos hordalékszállító képesség, valamint szemösszetétel mutatható ki (sarkantyúk között iszap; a főmederben durva kavics és mederpáncél). Ezen jelenségek jelentősen összetettebb morfodinamikai folyamatokat eredményeznek, mint ami az alsó- és felsőszakasz jellegű medreknél tapasztalható. Az elmúlt évtizedekben a Bősi-vízlépcső alatti szakasz jelentős mederváltozáson ment keresztül; néhol méteres medermélyüléseket, máshol kavicspadok kialakulását, a sarkantyúk között pedig feliszapolódást okozva [7], [8], [T3]. A jövőben bekövetkező szakasz- és helyi léptékű mederváltozások megbízható előrejelzésére komoly igény mutatkozik (pl. hajózás, vízgazdálkodás, árvízlevezető-képesség vizsgálata szempontjából), amelyre eddig csak közelítő tanulmányok készültek.

PhD-kutatásom célját ezek alapján fogalmaztam meg: olyan numerikus morfodinamikai modell elkészítését szerettem volna megvalósítani, amellyel jelentősen megbízhatóbban végezhető el a magyarországi Felső-Duna mederváltozásának vizsgálata, a korábbi tanulmányokban alkalmazott eljárásokhoz képest.

A numerikus vizsgálat sarkalatos pontja volt a hordaléktranszport-modell megválasztása. Előzetes vizsgálataim alapján rámutattam arra, hogy a szakirodalomban fellelhető modellek csak a finomabb szemcsék vagy a durvább kavicsok mozgását írják le megbízhatóan; a két jelenség egyidejű számbevételére alkalmas hordaléktranszport- modell nem állt rendelkezésemre.

Beláttam, hogy a numerikus vizsgálat elvégzéséhez olyan új hordaléktranszport-számítási eljárás kidolgozására van szükség, amely a homok (sarkantyúk közötti homokos terület), a kavics (főmeder) és azok keverékének (gázlók) mozgását egyidejűleg képes számítani.

Módszerek

A megelőző tanulmányok alapján igazoltam, hogy a Wilcock and Crowe-modell alkalmas a mederpáncélozódásának vizsgálatára [T2].

 

 

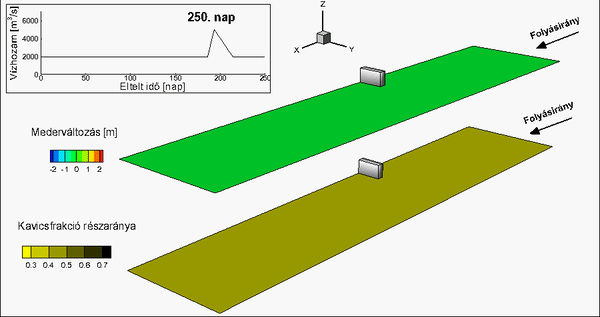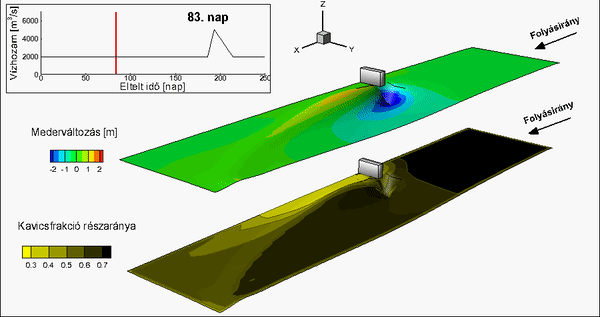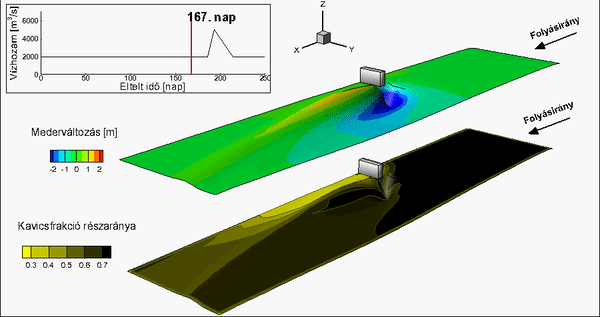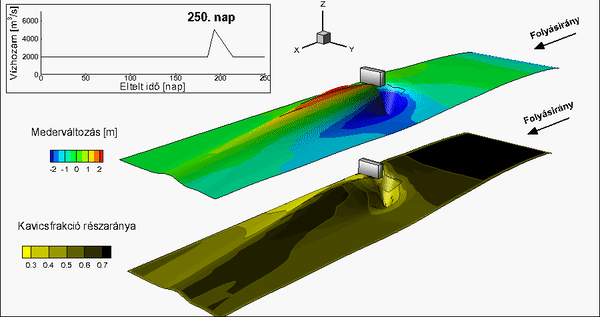
A homok transzportjának leírására pedig a van Rijn-modell alkalmazandó. Ezek alapján világossá vált, hogy a Felső-Duna-szakasz numerikus vizsgálatához új hordaléktranszport-számítási eljárás kidolgozása szükséges, amely megbízhatóan képes számítani a térben és időben is változatos szemösszetételű hordalékmozgást.

Az új eljárás alapgondolata: a számítási rácsháló egy adott cellájában a hordaléktranszportot az a hordaléktranszport-modell számítsa, amelyiktől az alkalmazhatósági korlátai alapján a pontosabb eredmény várható. Ennek megfelelően az új eljárás tulajdonképpen két, a homokra (van Rijn) és a kavicsos (Wilcock and Crowe) hordalékmozgásra kidolgozott hordaléktranszport-modell optimálisan összekapcsolt, párhuzamos alkalmazását jelenti [T4].

A módszer kidolgozásához szükségem volt egy olyan általánosan alkalmazható feltétel megfogalmazására, amely automatikusan dönti el, hogy az adott számítási cellában a homok vagy a kavics transzport dominál adott vízjárási állapot esetén (vagyis hogy a van Rijn, vagy a Wilcock and Crowe-modell aktiválódjon). A szakirodalomban a Shields-Parker-diagram [9] található, ami az ún. részecske-Reynolds-szám (Re_p) függvényében mutatja meg, hogy a homok- vagy a kavicstranszport dominál. Az eljárás viszont csak homogén szemösszetétel esetén alkalmazható.

Shields [1], valamint Wilcock, Kenworthy és Crowe [10] laboratóriumi méréseinek leírását, valamint van Rijn [5] tapasztalatait tanulmányozva azt feltételeztem, hogy az ún. csúsztató Reynolds-szám (Re^*) alkalmas indikátora a domináns hordaléktranszport-jellegnek vegyes szemösszetétel esetén.

Eddigi eredmények

Az új hordaléktranszport-modellezési eljárás igazolását három lépésben végeztem el:

 

1.     A csúsztató Reynolds-szám-alapú domináns hordaléktranszport-jelleget meghatározó eljárás igazolása:

 

Az alábbi hipotézis került megfogalmazásra:

• Re^* < ~300 → homoktranszport dominál,

• Re^* > ~400 → kavicstranszport dominál,

• ~300 < Re^* < ~400 → kavics lerakódása és kavicspad épülése várható.

 

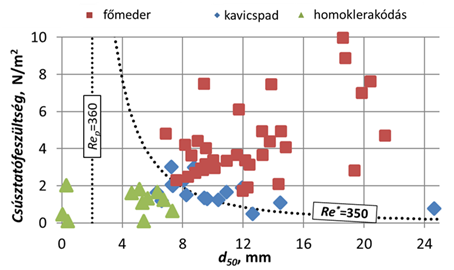
2. ábra: Terepi és laboratóriumi mérésekből származtatott, összetartozó csúsztatófeszültség – átlagos szemcseméret (d₅₀) értékpárok [T5], [T6]

 

Az igazolást saját, illetve szakirodalomban fellelhető laboratóriumi és terepi mérésekből származó adatok alapján végeztem el. Az ábra alapján látható, hogy a Re^* függvényében szétválaszthatók a zöld (homoktranszport), a kék (kavicslerakódás) és piros (kavicstranszport) pontfelhők. Vagyis, ellentétben a Shields-Parker-diagrammon alapuló osztályozással (Re_p = 360) az Re^* függvényében vegyes szemösszetétel esetén eldönthető, hogy a homok vagy a kavics dominál a görgetett hordalékmozgásban [T5], [T6].

 

2.     A van Rijn és a Wilcock and Crowe hordaléktranszport-modelljeinek összekapcsolt alkalmazásán alapuló újszerű eljárás igazolása saját laboratóriumi méréseim alapján:

 

A numerikus modelleredmények laborméréseimmel [T7] való összevetése alapján bemutattam, hogy olyan összetett morfodinamikájú csatorna esetén, amelyben mederpáncélozódás, homoklerakódás és vegyes szemösszetételű hordalék mozgása is megjelenik, a van Rijn- és a Wilcock and Crowe-modellek összekapcsolt alkalmazása pontosabban számítja a mederváltozást, mint az azok külön alkalmazásával felépített modellek.

 

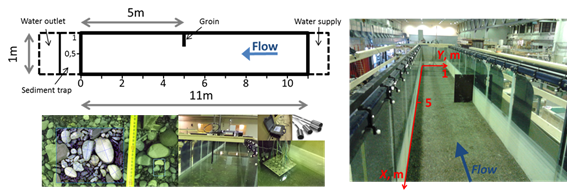
3. ábra: Laboratóriumi vizsgálatok a trondheimi Norvég Műszaki Egyetem Hidraulikai Laboratóriumában [T7]

 

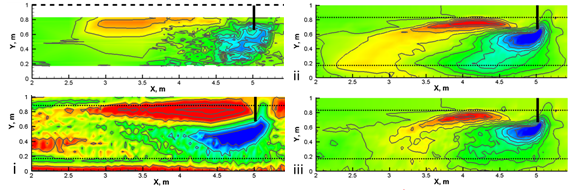
4. ábra: Mért (bal felső) és modellezett (i- van Rijn, ii – Wilcock and Crowe és iii – új eljárás) mederváltozás-térképek [T4]

 3.        Az összekapcsolt alkalmazáson alapuló újszerű eljárás igazolása a Duna 1794 fkm – 1799 fkm közötti szakaszára, terepi mérések alapján:

 

A hordaléktranszport-modellek együttes alkalmazásán alapuló új eljárás valós folyószakaszra való igazolásához elkészítettem egy 3D numerikus modellt a Duna 1794 fkm – 1799 fkm közötti szakaszára. A modell paraméterezéséhez és a peremfeltételek definiálásához saját, illetve az ÉDUVIZIG terepi méréseit használtam fel. A modell segítségével azt vizsgáltam, hogy hogyan változik a meder 2012 és 2014 között a mért nagyvízi (Q > 2100 m³/s) vízjárás hatására. A kapott eredményt a 2012 és 2014 között mért mederváltozás-térkép alapján értékeltem.

A mért és modellezett mederváltozások alapján kimutattam, hogy az újszerű eljárás pontosabban becsüli a mederváltozásokat, mint a van Rijn vagy a Wilcock and Crowe leírások külön alkalmazásával felépített modellek.

 

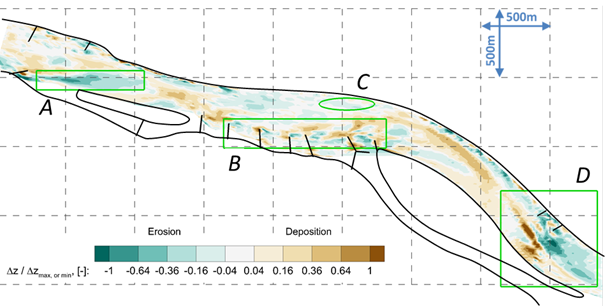
5. ábra: 2012 és 2014 októbere között időszakra mért normált (a kimélyüléseket a legnagyobb kimélyüléssel, a lerakódásokat a legnagyobb lerakódással normált) mederváltozás a vizsgált Duna-szakaszra

 

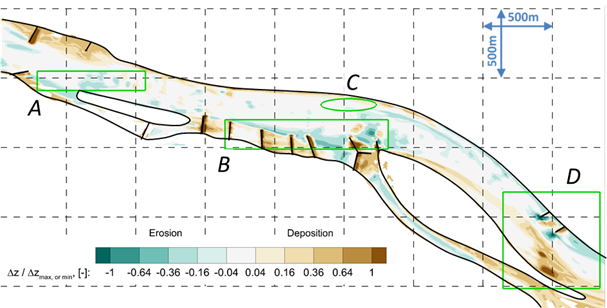
6. ábra: A 2012 és 2014 októbere közötti időszakra számított normált (a kimélyüléseket a legnagyobb kimélyüléssel és lerakódásokat a legnagyobb lerakódással normált) mederváltozás a vizsgált Duna-szakaszra

Várható impakt, további kutatás

Az újszerű hordaléktranszport-modellezési eljárástól olyan vizsgálatok elvégzését várom, amelyeket a korábbi hordaléktranszport-modellek alkalmazása nem tett lehetővé összetett morfodinamikájú folyószakaszok esetén. Bár az új eljárástól sem várható a mederváltozás pontos becslése, a szakasz- és helyi léptékű mederváltozások vízhozam függvényében történő előrejelzése jelentősen pontosabban becsülhető. Erre mutat példát az alábbi ábra:

 

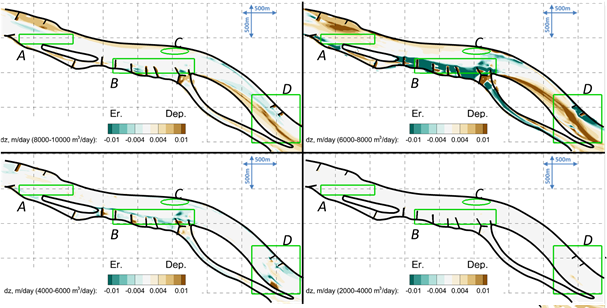
7. ábra: Várható napi mederváltozások négy vízhozam-tartományban

 

Saját publikációk, hivatkozások, linkgyűjtemény

Kapcsolódó saját publikációk listája.

 

[T1]    G. T. Török, “Vegyes szemcse-összetételű folyómedrek numerikus vizsgálata (Numerical investigation of non-uniform river bed),” Hidrológiai Tájékoztató, pp. 22–24, 2013.

[T2]    G. T. Török, S. Baranya és N. Rüther, “Three-dimensional numerical modeling of non-uniform sediment transport and bed armoring process,” in 18th Congress of the Asia & Pacific Division of the International Association for Hydro-Environment Engineering and Research 2012, 2012.

[T3]    G. T. Török és S. Baranya, “Morphological investigation of a critical reach of the upper Hungarian Danube,” Period. Polytech. Civ. Eng., vol. 61, no. 4, 2017.

[T4]    G. T. Török, S. Baranya és N. Rüther, “3D CFD Modeling of Local Scouring, Bed Armoring and Sediment Deposition,” Water, vol. 9, no. 56, p. 23 p., 2017.

[T5]    G. T. Török és S. Baranya, “Morphodynamic investigation of the Danube River by a novel sediment transport modelling method,” in 20th EGU General Assembly, 2018, vol. 20:15580.

[T6]    G. T. Török és S. Baranya, “A shear Reynolds number based sediment transport classification method for complex river beds,” in 8th International Symposium on Environmental Hydraulics, 2018.

[T7]    G. T. Török, S. Baranya, N. Rüther és S. Spiller, “Laboratory analysis of armor layer development in a local scour around a groin,” in Proceedings of the International Conference on Fluvial Hydraulics, RIVER FLOW 2014, 2014.

 

Hivatkozások listája.

 

[1]       A. Shields, “Application of Similarity Principles and Turbulence Research to Bed-Load Movement,” Mitt. Preuss. Versuchsanst. Wasserbau Schiffbau, vol. 26, no. 5–24, p. 47, 1936.

[2]       H. A. Einstein, “The Bed-Load Function for Sediment Transportation in Open Channel Flows,” Washington, 1950.

[3]       T. Fischer-Antze, N. Reidar B. Olsen, and D. Gutknecht, “Three-dimensional CFD modeling of morphological bed changes in the Danube River,” vol. 44, no. June, pp. 1–15, 2008.

[4]       N. Reidar B. Olsen, “A Three-Dimensional Numerical Model for Simulation of Sediment Movements in Water Intakes with Moving Option,” Trondheim, 2002.

[5]       L. C. van Rijn, “Sediment Transport, Part I: Bed Load Transport,” J. Hydraul. Eng., vol. 110, no. 10, pp. 1431–1456, 1984.

[6]       P. R. Wilcock és J. C. Crowe, “Surface-based transport model for mixed-size sediment,” J. Hydraul. Eng., vol. 129, no. 2, pp. 120–128, 2003.

[7]       L. Rákóczi, “A Duna hordalékjárása (Sediment load conditions of River Danube),” Vízügyi Közlemények, vol. 75, no. 2, pp. 128–146, 1993.

[8]       K. Holubová, Z. Capeková és J. Szolgay, “Impact of hydropower schemes at bedload regime and channel morphology of the Danube River,” in River Flow 2004: Proceedings of the Second International Conference on Fluvial Hydraulics, 2004, no. 1, pp. 135–142.

[9]       G. Parker, “Transport of Gravel and Sediment Mixtures,” in Sedimentation Engineering, M. Garcia, Ed. American Society of Civil Engineers, 2008, pp. 165–251.

[10]      Wilcock P.R., Kenworthy S.T. és Crowe J.C., “Experimental Study of the Transport of Mixed Sand and Gravel,” Water Resour. Res., vol. 37, no. 12, pp. 3349–3358, 2001.