Pál Vásárhelyi Doctoral School of Civil Engineering and Earth Sciences 

MTA-BME Water Management Research Group

Supervisor: Dr. Baranya Sándor

Methodological Improvement of Morphodynamic Modeling of River Beds with Non-Uniform Material

Introducing the research area

The geometry and the bed material content of large rivers can change significantly, both in time and space. These morphological processes are caused mainly by the varied flow pattern. However, the changed bed geometry and bed material also affect the flow field. Therefore, the investigation of the continuous interaction between the riverbed and the flow is necessary in order to reveal the current processes and to estimate the potential bed changes. As the rivers have many life-helping functions (e.g. providing drinking water, inland navigation, energy production, irrigation, and fishing), an increasing demand has arisen on the part of river users to gain trustworthy knowledge on the future spatial and temporal variation of the river morphology.

Brief introduction of the research place

My PhD work has been carried out in the MTA-BME Water Management Research Group. The morphodynamics related investigation of the Hungarian Danube is one of the most essential research topics of the Group. Up-to-date measuring instruments are available, which facilitates the elaboration of high quality field measurements. Moreover, the numerical modeling of morphological processes is another acknowledged and focused topic.

History and context of the research

An intensive research on sediment transport and river morphology started in the middle of the 20th century. Initially, based on laboratory measurements, many researchers developed empirical and semi-empirical formulas for the approximation of the sediment transport and conditions. These simple methods estimate the sediment load as a function of a few sediment and flow related parameters, e.g. d₅₀ (median grain size), h (water depth) or v (flow velocity), resulting in a rough estimate. However, it is essential to emphasize that the applicability of these formulas is limited to less complex situations; to apply them for more complex morphodynamic situations (e.g. complicated and sinuous geometry, non-uniform bed material, variable morphological features both in time and space) is not a trustworthy alternative [1], [2]. Later, the intensive development of computing capacity and the evolution of flow modeling enabled the treatment of longer river sections [3], [4], [T1], [T2].

 

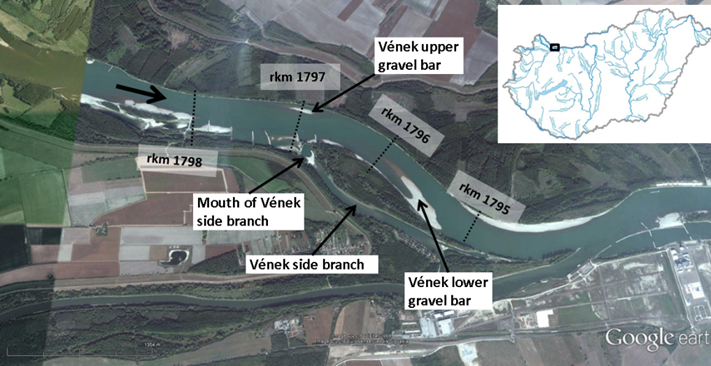
Fig. 1    The Hungarian Upper Danube reaches between rkm 1794 and rkm 1799.

 

However, even the most common and most reliable sediment transport formulas were developed focusing on one defined nature of sediment movement. For instance, the van Rijn formula [5] can be used for the calculation of the sand movement, while the Wilcock and Crowe model [6] describes gravel motion dominated situations (for instance, for the investigation of the bed armoring process [T2]).

In relatively rare cases there are considerable lengths of rivers where this dividing is not trivial. This is usually the case at transitional sections between the sand-bed and gravel-bed reaches, where the flow pattern results in spatially largely varied bed content (coarse bed surface in the main stream and sand bed at the near-bank places). In similarly complex and varied morphological cases, it is difficult to decide which sediment transport formula will be the most reliable. That is to say, there is still no generally applicable method to describe the related combined morphodynamic processes.

The research goals, open questions

The Hungarian Upper-Danube has a sinuous middle course pattern type with non-uniform sand/gravel bed material. Beside the natural facilities, the artificial interventions installed in the last decades also enhanced the complexity of the morphological processes. This means that a spatially and temporally varied sediment transport capacity and bed content evolved (sand aggradation in the groin fields and bed armoring in the main stream). Also noted, that the morphological variation became even more problematic after the hydropower plant at Gabcikovo, Slovakia was constructed resulting in up to 1-2 m bed level incision and gravel bar formations in the downstream [7], [8], [T3]. Therefore, an increasing demand has arisen on the part of the river users (e.g. navigation, water management, flood wave protection) to gain trustworthy knowledge on the future spatial and temporal variation of local- and reach-scale river morphology.

Based on the above described situation, my PhD project aims at elaborating a morphodynamic numerical model which offers a more suitable and significantly more reliable tool for the investigation of the bed changes in the Hungarian Upper-Danube, compared to the earlier applied numerical methods.

Based on my earlier studies I showed that the proper choice of the sediment transport model is a pivotal point in numerical modeling. Most of the sediment transport models have been validated and operate reliably either for finer sand, or coarser grains; there is still no generally applicable method to describe the process if both sand and gravel transport are simultaneously present.

I realized that to complete the numerical investigations, a novel sediment transport investigation method was required, which is capable of reliably calculating the transport of the sand (fine material aggradation in the groin fields), the gravel (main stream) and the sand/gravel mixture (e.g. bar formations), simultaneously.

Methods

Based on preliminary studies I confirmed that the Wilcock and Crowe model is able to describe the mechanism of the selective erosion phenomenon [T2].

 

 

On the other hand, the van Rijn model is more suitable for calculating the sand transport. Therefore, it became clear that a novel sediment transport modeling method is needed, which can provide estimates on the sediment transport in spatially and temporally varied river beds.

The basic concept of the novel method: The cornerstone of the novel method is that the sediment transport is calculated everywhere in the investigated channel reach by the sediment transport formula, which promises a more reliable description of the local morphodynamic features. Accordingly, the novel method actually means the parallel application of the optimally connected van Rijn and the Wilcock and Crowe sediment transport models [T4]. However, a suitable criterion had to be formulated, which helps choose automatically the dominant nature of sediment transport (gravel or sand dominated one) that can be observed at a given place. Based on this classification, a suitable criterion is able to decide which sediment transport formula (W&C or vR) should to activated. The literature contains the Shields-Parker diagram [9], which demonstrates that the dominant sediment transport nature in a channel can reliably be determined as the function of the so called explicit particle Reynolds number (Re_p), in the case of uniform bed material. However, in the case of non-uniform bed material together with complex flow- and morphological features, this method, or the application of characteristic grain sizes, e.g. d₅₀, d₉₀, involves high uncertainty.

Based on the description of the laboratory experiments of Shields [1] and Wilcock, Kenworthy és Crowe [10] and the experiences of van Rijn [5] it was assumed that the shear Reynolds number (Re^*) is able to refer to the locally dominant sediment transport nature in the case of non-uniform bed materials even within a morphologically varied river section.

Results

The validation of the novel sediment transport modeling method was elaborated in three steps:

 

1.     Validation of the process used for determining the shear Reynolds number based nature of the sediment transport:

 

The following hypothesis was formulated:

• Re^* < ~300 → sand transport dominates,

• Re^* > ~400 → gravel transport dominates,

• ~300 < Re^* < ~400 → gravel accumulating and gravel bar formation is expected.

 

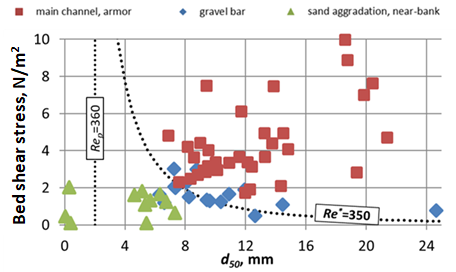
Fig. 2 The corresponding bed shear stress values as the function of the d₅₀ grain sizes from field and laboratory measurements [T5], [T6].

 

The validation was accomplished based on laboratory and field measurement data. It can be seen in Fig. 2, that the points from the three well distinguishable regions (green, red and blue markers) indeed show different features (sand dominated, gravel dominated transport, gravel accumulation). In this way I demonstrated that the shear Reynolds number (Re^*) is a more adequate parameter than the explicit particle Reynolds number (Re_p) to decide if the sand or the gravel dominates locally in the bed load sediment transport [T5], [T6].

 

 

1.     Validation of the novel combined method (the parallel use of the van Rijn and the Wilcock and Crowe bed load transport formulas) based on laboratory experiments:

 

Numerical simulation results were compared to laboratory measurements with complex flow- and morphological features [T7] (bed armoring and sand aggradation can occur simultaneously). Based on this investigation, I demonstrated that the combined application of the van Rijn and the Wilcock and Crowe models gives more reliable result for the bed change than the separate application of the formulas.

 

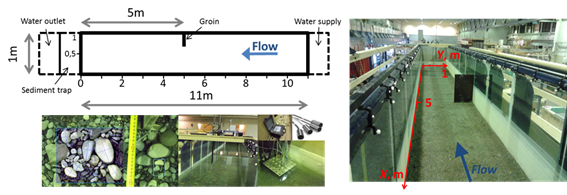
Fig. 3   Laboratory experiments at the laboratory of the Norwegian University of Science and Technology [T7].

 

Fig. 4 Measured (top left) and calculated (i – van Rijn, ii – Wilcock and Crowe and iii – novel method) bed change maps [T4]

 

1.     Validation of the novel combined method based on field measurements at the Danube reach between rkm 1794 and rkm 1799:

 

To validate the novel sediment transport calculation method for real study case, I carried out the 3D numerical morphodynamic investigations of the Danube River between rkm 1794 and 1799. The model was parameterized based on the field measurements of the North-Transdanubian Water Directorate and own field measurements. The goal was to analyze the accuracy of the novel method. Therefore, the calculated bed change map for higher flow regimes (if Q > 2100 m³/s) in the period between 2012 and 2014 (including the historical flood wave in 2013) was compared to the measured map.

The results suggest that the bed changes are estimated more reliably by the combined method than any one of the van Rijn or the Wilcock and Crowe formulas applied separate.

 

 

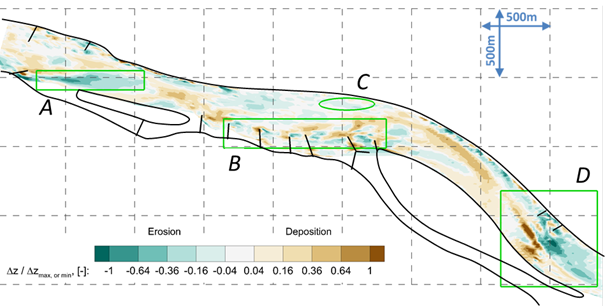
Fig. 5 Normalized (by the highest bed level decrease or increase value) bed changes of the measured values regarding to the whole period of 2012 October – 2014 October.

 

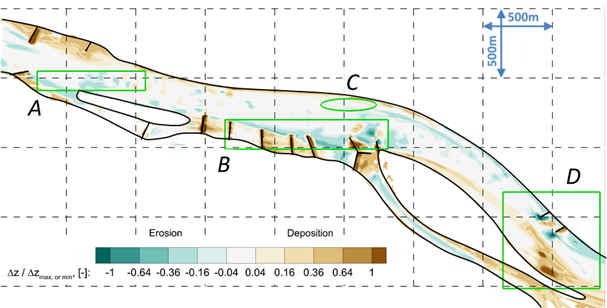
Fig. 6 Normalized (by the highest bed level decrease or increase value) bed changes of the calculated bed changes regarding the period of 2012 October – 2014 October.

 

Expected impact and further research

According to my expectations, the novel sediment transport modeling method supports such morphodynamic investigations of complex morphodynamic river beds which could not have been completed by the former sediment transport models. Although the novel method also introduces some inaccuracy, it is proven to be a suitable investigation methodology for the analysis of future restoration measures, such as local- and reach-scale morphodynamic processes, moreover, the interaction mechanism between the two scales can be revealed. Such kind of examination example can be seen in the following Figure.

 

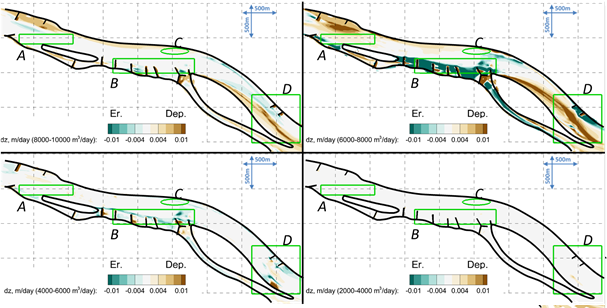
Fig. 7   Daily average bed change maps for four discharge ranges.

 

Publications, references, links

List of corresponding own publications

 

[T1]    G. T. Török, “Vegyes szemcse-összetételű folyómedrek numerikus vizsgálata (Numerical investigation of non-uniform river bed),” Hidrológiai Tájékoztató, pp. 22–24, 2013.

[T2]    G. T. Török, S. Baranya, and N. Rüther, “Three-dimensional numerical modeling of non-uniform sediment transport and bed armoring process,” in 18th Congress of the Asia & Pacific Division of the International Association for Hydro-Environment Engineering and Research 2012, 2012.

[T3]    G. T. Török and S. Baranya, “Morphological investigation of a critical reach of the upper Hungarian Danube,” Period. Polytech. Civ. Eng., vol. 61, no. 4, 2017.

[T4]    G. T. Török, S. Baranya, and N. Rüther, “3D CFD Modeling of Local Scouring, Bed Armoring and Sediment Deposition,” Water, vol. 9, no. 56, p. 23 p., 2017.

[T5]    G. T. Török and S. Baranya, “Morphodynamic investigation of the Danube River by a novel sediment transport modelling method,” in 20th EGU General Assembly, 2018, vol. 20:15580.

[T6]    G. T. Török and S. Baranya, “A shear Reynolds number based sediment transport classification method for complex river beds,” in 8th International Symposium on Environmental Hydraulics, 2018.

[T7]    G. T. Török, S. Baranya, N. Rüther, and S. Spiller, “Laboratory analysis of armor layer development in a local scour around a groin,” in Proceedings of the International Conference on Fluvial Hydraulics, RIVER FLOW 2014, 2014.

 

List of references

 

[1]       A. Shields, “Application of Similarity Principles and Turbulence Research to Bed-Load Movement,” Mitt. Preuss. Versuchsanst. Wasserbau Schiffbau, vol. 26, no. 5–24, p. 47, 1936.

[2]       H. A. Einstein, “The Bed-Load Function for Sediment Transportation in Open Channel Flows,” Washington, 1950.

[3]       T. Fischer-Antze, N. Reidar B. Olsen, and D. Gutknecht, “Three-dimensional CFD modeling of morphological bed changes in the Danube River,” vol. 44, no. June, pp. 1–15, 2008.

[4]       N. Reidar B. Olsen, “A Three-Dimensional Numerical Model for Simulation of Sediment Movements in Water Intakes with Moving Option,” Trondheim, 2002.

[5]       L. C. van Rijn, “Sediment Transport, Part I: Bed Load Transport,” J. Hydraul. Eng., vol. 110, no. 10, pp. 1431–1456, 1984.

[6]       P. R. Wilcock and J. C. Crowe, “Surface-based transport model for mixed-size sediment,” J. Hydraul. Eng., vol. 129, no. 2, pp. 120–128, 2003.

[7]       L. Rákóczi, “A Duna hordalékjárása (Sediment load conditions of River Danube),” Vízügyi Közlemények, vol. 75, no. 2, pp. 128–146, 1993.

[8]       K. Holubová, Z. Capeková, and J. Szolgay, “Impact of hydropower schemes at bedload regime and channel morphology of the Danube River,” in River Flow 2004: Proceedings of the Second International Conference on Fluvial Hydraulics, 2004, no. 1, pp. 135–142.

[9]       G. Parker, “Transport of Gravel and Sediment Mixtures,” in Sedimentation Engineering, M. Garcia, Ed. American Society of Civil Engineers, 2008, pp. 165–251.

[10]      Wilcock P.R., Kenworthy S.T., and Crowe J.C., “Experimental Study of the Transport of Mixed Sand and Gravel,” Water Resour. Res., vol. 37, no. 12, pp. 3349–3358, 2001.