George A. Olah Doctoral School of Chemistry and Chemical Technology 

Department of Physical Chemistry and Materials Science

Supervisor: Dr. Kállay Mihály

Efficient Excited-State Quantum Chemical Calculations of Large Molecules

Introducing the research area

The accurate theoretical modeling of excited state properties (electronic excitation energy, UV-visible spectra) of molecular systems is limited by the severe computational requirements of the presently available quantum chemical methods. Reasonably accurate calculations can only be performed for systems containing at most about 50 atoms within reasonable computation time. My goal is to develop approximate algorithms which can significantly reduce the computational costs, while preserving the intrinsic accuracy of the exact methods [M1-M3].

 

Brief introduction of the research place

My research is carried out at the Department of Physical Chemistry and Materials Science, BUTE under the supervision of Professor Mihály Kállay, head of department. The primary research focuses of our group are the development of quantum chemical methods and computational chemistry. This activity of the group has received significantly support in the past 10 years from research grants (ERC Starting Grant, Lendület and Élvonal Kutatói Kiválóság), which was essential to reach outstanding research goals in that period. The largest quantum chemical calculation taking electron correlation effects into account explicitly has also been completed in our laboratory [1].

 

History and context of the research

Our efforts for the development of quantum chemical calculations focus on the efficient and accurate solution of the Schrödinger equation. The first contributions to this field date back to the 1930s, but the breakthrough had come along only with advancements in algorithm design and the boost of computing performance, starting in around 1980 and still continues to grow in our days. Since then, the results achieved in quantum chemistry have been awarded with two Nobel Prizes in Chemistry. Over the past decade, one significant avenue of the developments has been the design of more accurate methods and to implement the corresponding complicated equations in the program packages, e.g. via automatic code generation techniques. Various highly accurate quantum chemical methods had been developed, which allowed the theoretical prediction or understanding of experimentally measurable physical and chemical properties, such as equilibrium structures, absorption spectra, or NMR parameters. The accuracy of the obtained results is comparable to that of the experiments, or more often even exceeds them.

However, the solution of the systems of equation containing billions of unknown variables is extremely demanding. For more elaborate methods, the number of variables scales as 7th or 8th power of the system size. It is easy to see that in the latter case, by doubling the size of the studied molecule, the time required for the calculations increases by a factor of 256. Therefore, the application of the most accurate methods is limited to molecular systems with up to a few atoms. Accordingly, a substantial aim of the method development in recent years is to reduce the calculation times of our highly reliable, existing methods.

 

The research goals, open questions

External perturbations, such as electromagnetic radiation, of certain strength can lead to the rearrangement of the electronic structure and to the excitation of one or more electrons. There are several phenomena actively researched nowadays that relate to the excited electronic states of molecular systems. For instance, excited states play an important role in photochromic materials, in photo-initialized chemical processes, and in energy transfer and storage. Quantum-chemical methods have now become routine tools in the investigation of excited-state properties and processes in the fields of spectroscopy [M4, M5], analytical- and biochemistry. Consequently, it is important to develop efficient but reliable approaches for the simulation of the excited states of realistic molecular systems. Our goal is to expand the existing limit of accurate excited-state methods and to model chemically relevant systems that cannot be treated currently due to extensive computational requirements.

The aim of our research is to introduce better algorithms and approximations on the basis of numerical mathematical methods, our numerical experience, and the available information technology (IT) infrastructure that can be used to perform faster calculations with less computational effort. In this case, the number of variables to be determined might either decrease or even increase. However, due to efficiently programmable and executable algorithms, the solution of the equations takes less time in both cases (see density fitting). In another group of mathematical transformations we carry out transformations controlled by specific physical or chemical considerations. In this case, we can effectively reduce the number of variables, such as the number of molecular orbitals, leading to a drastic reduction in the computational demand (see localized molecular orbitals). The final goal is to find and combine the most appropriate transformations and minimize the number of variables, until the error of approximations introduced by us will be an order of magnitude smaller on average than the intrinsic error of the original method.

 

Methods

Second-order algebraic-diagrammatic construction [ADC(2)] method

The hierarchical algebraic-diagrammatic construction (ADC) theory is suitable for calculating excited state properties and capable of taking into account the effect of electron correlation with arbitrary accuracy. The leading contribution is given by the ADC(2) method, which considers the electron correlation up to second order, therefore the calculations scale with the fifth power of the number of molecular orbitals [2].

 

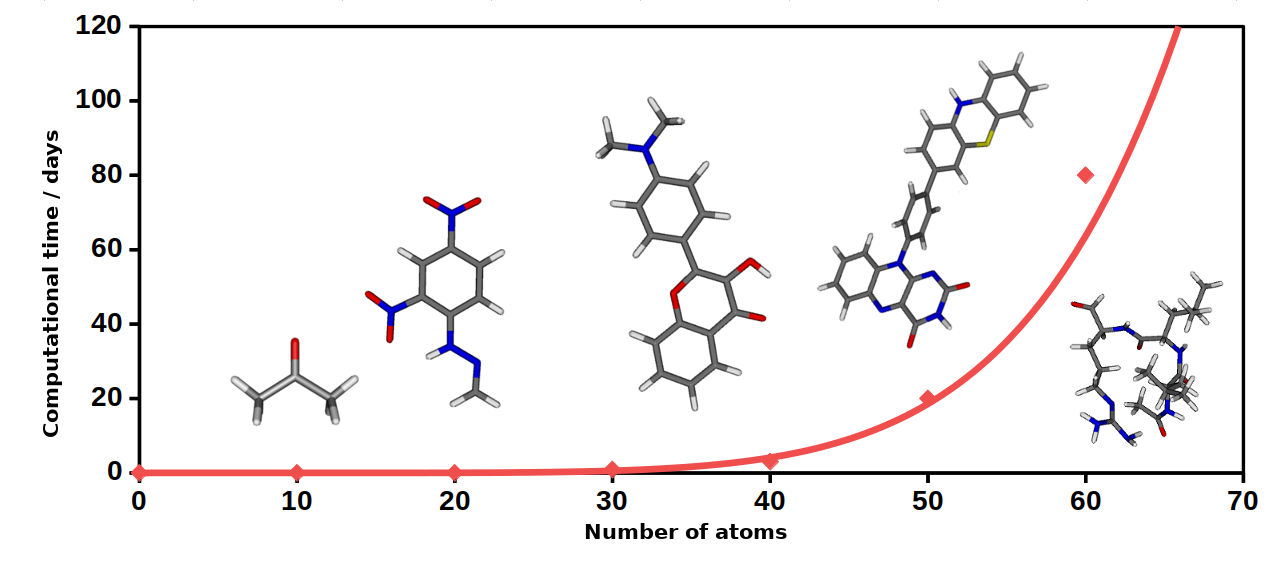
Fig. 1. The approximate time required for the ADC(2) calculations as a function of the system size.

 

The ADC(2) method has become more and more popular over recent years after it turned out that its formalism and accuracy are closely related to the most commonly employed second-order coupled-cluster (CC2) method [3, 4]. The great advantage of the ADC(2) method over the CC2 is that one solves a Hermitian eigenvalue problem during the calculations. Therefore, the right and left eigenvectors of the matrix equation are the same. The error of the method is about 0.2 - 0.3 eV on average compared to experimental results [5].

 

Basis set

For the calculations, Gaussian type functions are used, which are well suited to describe the electronic structure of atoms. The molecular orbitals are then expressed as linear combinations of the predetermined basis functions (LCAO-MO theory). In our case, Dunning’s correlation consistent basis sets (such as the aug-cc-pVTZ) [6] were utilized, which are appropriate for complicated, such as the Rydberg type of excitation

 

Density fitting

Conventionally, the so-called two-electron integrals, which describe the interaction of the electrons in our atomic orbital based model, are stored in extensive, four-indexed arrays. The size of these arrays can easily reach a couple of terabytes if the molecule of interest contains close to or more than 50 atoms. Obviously, this amount of data cannot be stored in the main memory, such arrays only fit on hard disks. In that case the integrals have to be retrieved over and over again from the hard disk in many steps of the calculation. In the density fitting approach [7], the four-indexed electron repulsion integrals are written in an approximate form as the products of two- and three-center integrals. The size of the corresponding arrays is “only” a few gigabytes and can be easily stored in the memory. With modern computers it is faster to reproduce the necessary four-center integrals using their density-fitted form multiple times than to read them from relatively slow hard disks. Therefore, the storage requirements, and the number of the input-output operations can be greatly reduced.

 

Natural orbitals

In the case of the natural orbital (NO) approximation [8], a one-particle density matrix is constructed from the corresponding wave function and diagonalized. The eigenvectors of this matrix are the natural orbitals, while its eigenvalues are interpreted as the corresponding occupation numbers of the natural orbitals. The NOs with smaller occupation numbers usually give a smaller contribution to correlation energies. It has been shown that natural orbitals can lead the most compact representations of the exact wave function, if the latter is expressed in a certain form. A widely used cost-reduction technique is that the density matrix is constructed using a less accurate, but more economical method and the orbitals with smaller contribution are dropped from the resulting basis. Thereafter, we only use these most important NOs obtained from the cheaper method to perform more elaborate calculation. Thus a significant gain is realized by reducing the number of variables.

 

Localized molecular orbitals

The interaction energy between electrons in molecular systems decreases with the sixth power of the distance between the particles. This phenomenon is not apparent if working with canonical molecular orbitals; they spread over the entire molecule. If the orbitals are localized via a sufficient algorithm, the proper, fast decay of interaction energies with distance can be recovered. While all contributions are considered in the exact case, we can neglect these integrals with small contributions in a local representation. This further reduces significantly the computation time, whereas accuracy merely decreases negligibly. [9].

 

 

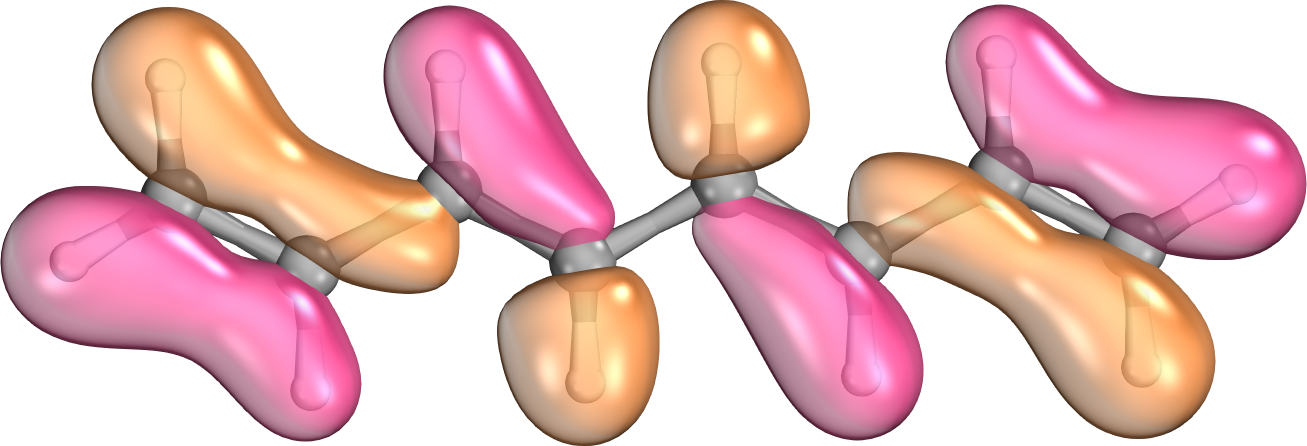
Fig. 2. A canonical (left) and a localized (right) molecular orbital of octatetraene.

 

Results

We have successfully derived a density matrix which is suitable for obtaining highly compressed but still accurate natural orbital basis for excited-state calculations. The formula of the matrix is not trivial, because equations have to be solved for both the ground and the excited state simultaneously working with the same NO basis. Our investigations concluded that it is ideal to use a so-called state-averaged density matrix which is the average of the second-order Møller-Plesset (MP2) and the configuration interaction singles with perturbative doubles [CIS(D)]- density matrices. We found that about 60% of the natural orbitals of such density matrix can be dropped without introducing a significant error to the excitation energy, while the original excitation energies are recovered within 0.02 eV on the average.

 

 

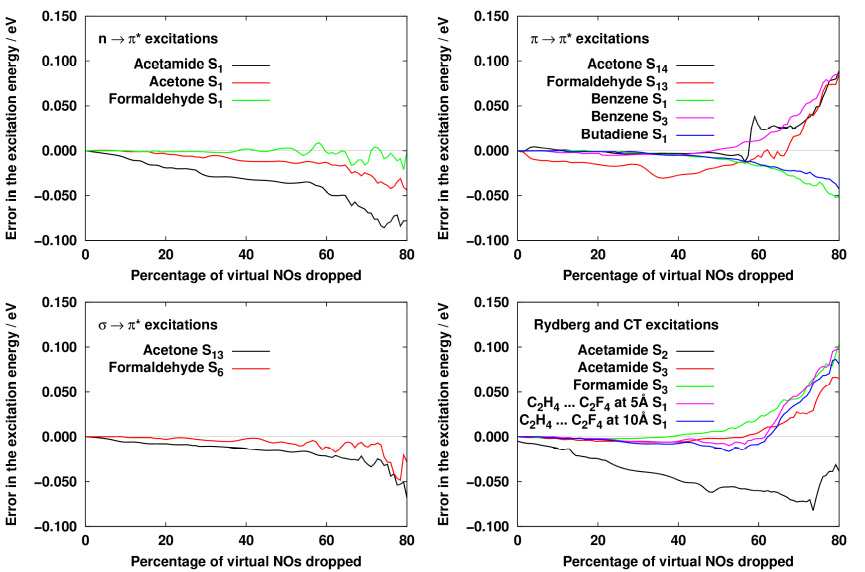
Fig. 3. The errors given in the excitation energy as a function of the natural orbitals dropped.

 

In addition, the natural auxiliary function (NAF) approximation, which was developed in our group, has been applied for the first time for excited state calculations. In this case, the fitting basis is compressed similarly to that in the natural orbital approximation. The main difference is that the NAF approximation is based on principles borrowed from numerical mathematics, whereas employing NOs involves certain physical motivations, too. The success of the NAF approach can be best understood on the example of digital image processing. In this case, one can perform singular value decomposition on a picture stored in a pixel-based format. Thereafter, the obtained contributions to the picture can be sorted according to increasing importance. The least important points can be neglected without changing the quality of the image for the human eye, while the size of the stored file will be much smaller.

 

 

Fig. 4. While the left (bmp) image size is 760 kilobytes, the right image (jpg) is 45 kilobytes.

 

In our case, the pixels are analogous to the auxiliary functions used for density fitting, the number of which can be greatly reduced while the quality of the fitted integrals stays similar to the original. The NAF approximation is practically error-free from the perspective of observable quantities. We found that the number of NAFs can be up to 80% smaller than the total number of auxiliary functions. This is understandable since by working with the NO basis the number of molecular orbitals has also decreased by 60%. By performing benchmark calculations on large molecules of up to 40 atoms we found that the excited-state equations can be solved 35 times faster compared to the exact calculations. The memory requirement is also reduced to a similar extent. While the overhead due to evaluation of the natural orbitals and auxiliary functions is notable, the overall speed-up is still a factor of 15 on the average [M1, M2]. The resulting reduced-cost approach has been successfully applied to the theoretical calculation of absorption spectra of extended molecules in the ultraviolet-visible (UV-VIS) region.

 

 

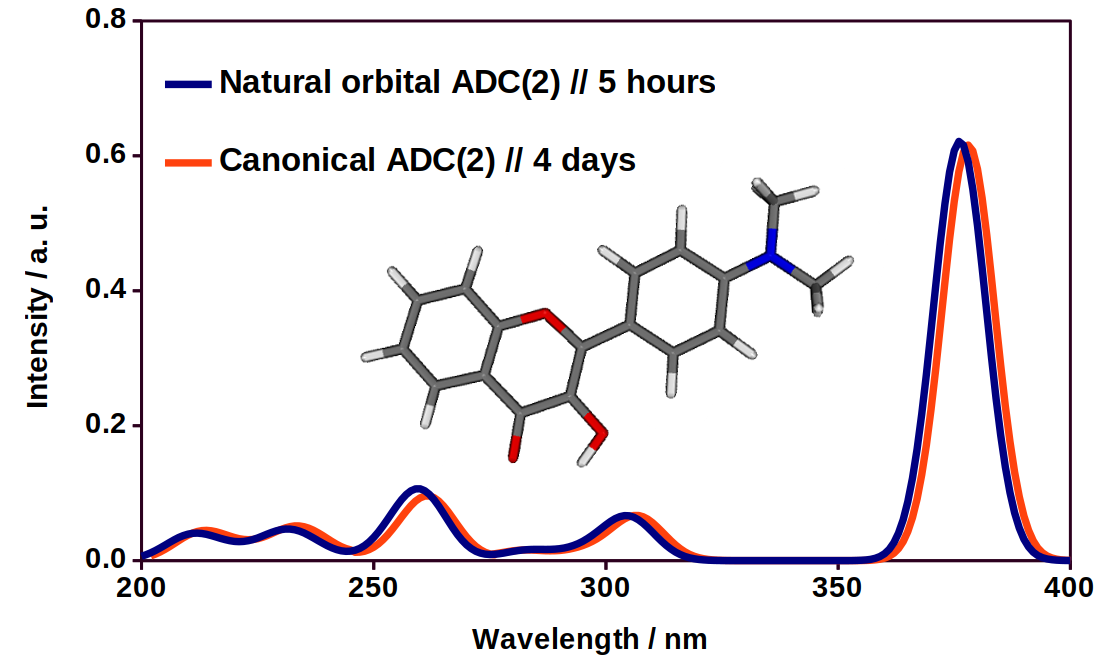
Fig. 5. An UV-VIS spectra of a flavone derivative using the exact and the approximate method.

 

The current application limit of our scheme with suitable large basis sets and a single processor workstation is between 100 and 150 atoms.

 

Fig. 6. The structure of an organic dye containing 127 atoms.

 

Presently, we are implementing the combination of local approximations with the cost-reducing approaches presented above [M3]. In this case, first, the most important molecular orbitals involved in an excitation are determined using a lower order (e.g. CIS) method. This orbital list is extended with additional orbitals on the basis of other criteria, such as distance between two orbitals, locality of the orbitals, or the strength of their interaction. Next, the more involved but more accurate calculations are performed in this restricted orbital space. The size of the given subspace is significantly smaller than the entire molecule. Our preliminary results suggest that, the local method is 3 times more efficient than the reduced-cost (45 times faster compared to the exact method), while the average error compared to the exact reference is only 0.03 eV. This error is still an order of magnitude smaller than the intrinsic error of the exact method. Consequently, using the same hardware the local approach extends the reach of our methods further, to systems with more than 200 atoms.

 

 

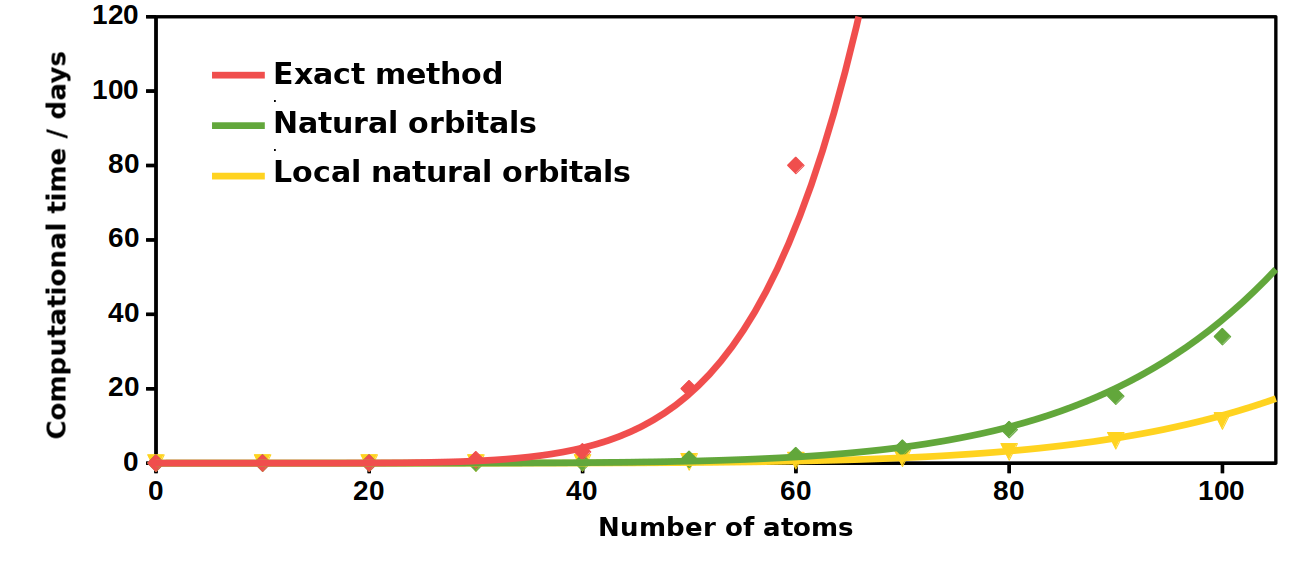
Fig. 7. The approximate computational time required using the various methods.

 

Expected impact and further research

Our goals in the near future include the optimization of the algorithm used in local approximations and to perform further benchmark calculations. We expect to achieve significant improvements in the efficiency of our final local scheme, that would allow us to calculate the accurate excited state properties of systems with hundreds of atoms, such as fluorescent proteins.

Both schemes are available for the scientific community as part of the Mrcc program suite [M6] developed in our laboratory. Free, open-source license is available for academic use. The program is used by hundreds of scientists around the world. The algorithm can be employed for the calculation of excitation energies and absorption- or circular dichroism spectra in the organic, biomolecular and photochemical fields, and to investigate the rearrangement in the charge distribution upon excitation, or to identify the molecular orbitals characteristic of the excitation. Our algorithms and approximations have already been adopted by several research groups. The developed framework is quite general and flexible; hence it can be utilized in numerous related quantum chemical approaches with minor modifications. A couple of them, e.g., the development of a local EOM-CCSD implementation, or efficient double-hybrid TD-DFT methods, are also on our schedule for the near future.

 

Publications, references, links

List of relevant own publications

[M1]: D. Mester, P. R. Nagy, and M. Kállay, J. Chem. Phys., 148, p. 094111, 2018. (IF: 2.965)

[M2]: D. Mester, P. R. Nagy, and M. Kállay, J. Chem. Phys., 146, p. 194102, 2017. (IF: 2.965)

[M3]: D. Mester, P. R. Nagy, and M. Kállay, in preparation.

[M4]: D. Hessz, M. Bojtár, D. Mester, Z. Szakács, I. Bitter, M. Kállay, and M. Kubinyi, Spectrochimica Acta Part A, 203, p. 96, 2018. (IF: 2.536)

[M5]: P. Bagi, K. Juhász, I. Tímári, K. E. Kövér, D. Mester, M. Kállay, M. Kubinyi, T. Szilvási, P. Pongrácz, L. Kollár, K. Karaghiosoff, M. Czugler, L. Drahos, E. Fogassy, and G. Keglevich, J Organom. Chem., 797, p. 140, 2015. (IF: 2.336)

[M6]: Mrcc, a quantum chemical program suite written by M. Kállay, Z. Rolik, J. Csontos, P. Nagy, G. Samu, D. Mester, J. Csóka, B. Szabó, I. Ladjánszki, L. Szegedy, B. Ladóczki, K. Petrov, M. Farkas, P. D. Mezei, and B. Hégely.

 

List of further own publications

[M7]: M. Bojtár, P. Z. Janzsó-Berend, D. Mester, D. Hessz, M. Kállay, M. Kubinyi, and I. Bitter, Beilstein J. Org. Chem., 14, p. 747, 2018. (IF: 2.337)

[M8]: J. Hári, P. Polyák, D. Mester, M. Micusik, M. Omastova, M. Kállay, and B. Pukánszky, App. Clay Sci., 132-133, p. 167, 2016. (IF: 3.101)

[M9]: D. Mester, J. Csontos, and M. Kállay, Theoretical Chemistry Accounts, 134, p. 74, 2015. (IF: 1.806)

 

Table of links

Mrcc program suite

Quantum chemistry

Electron correlation

Nobel Prizes in quantum chemistry: 1, 2

Excited state

Photochromism

Basis set

LCAO-MO theory

Localized molecular orbital

MP2 method

UV-VIS spectroscopy

 

List of references

[1]: P. R. Nagy, G. Samu, and M. Kállay, J. Chem. Theory Comput., 12, p. 4897, 2016.

[2]: J. Schirmer, Phys. Rev. A, 26, p. 2395, 1982.

[3]: C. Hättig, Adv. Quant. Chem., 50, p. 37, 2005.

[4]: O. Christiansen, H. Koch, and P. Jørgensen, Chem. Phys. Lett., 243, p. 409, 1995.

[5]: O. Christiansen, H. Koch, P. Jørgensen, and J. Olsen, Chem. Phys. Lett., 256, p. 185, 1996.

[6]: T. H. Dunning Jr., J. Chem. Phys., 90, p. 1007, 1989.

[7]: S. F. Boys, G. B. Cook, C. M. Reeves, and I. Shavitt, Nature, 178, p. 1207, 1956.

[8]: W. Meyer, J. Chem. Phys., 58, p. 1017, 1973.

[9]: P. Pulay, Chem. Phys. Lett., 100, p. 151, 1983.