|
|
BMe Kutatói pályázat |
|
Oláh György Doktori Iskola
Fizikai Kémia és Anyagtudományi Tanszék
Témavezető: Dr. Kállay Mihály
Nagy molekulák gerjesztett állapotainak hatékony kvantumkémiai számítása
A kutatási téma néhány soros bemutatása
A gerjesztett állapotú tulajdonságok (elektrongerjesztési energia, ultraibolya-látható spektrum) pontos, elméleti úton történő meghatározása a kvantumkémiai módszerek nagy számításigénye miatt jelenleg csak 50 atomnál kisebb molekuláris rendszerek esetén lehetséges belátható számítási időn belül. Célom olyan közelítő eljárások kidolgozása, amelyekkel a számításokhoz szükséges idő nagymértékben csökkenthető a módszerekre jellemző pontosság megtartása mellett [M1-M3].
A kutatóhely rövid bemutatása
Kutatásaimat a BME Fizikai Kémia és Anyagtudományi Tanszékén végzem dr. Kállay Mihály tanszékvezető egyetemi tanár irányításával. A csoport elsődlegesen kvantumkémiai módszerek fejlesztésével, illetve számításos kémiával foglalkozik. A csoportvezető és a kutatócsoport által elért, nemzetközi szinten is kiemelkedő eredmények létrehozását az elmúlt 10 évben számos, többek között az ERC Starting Grant, a Lendület és az Élvonal – Kutatói Kiválósági pályázat segítette. A jelenlegi legnagyobb elektronkorrelációt tartalmazó kvantumkémiai számítást is csoportunk végezte el [1].
A kutatás történetének, tágabb kontextusának bemutatása
A kvantumkémiai számítások során a Schrödinger-egyenlet minél pontosabb és gyorsabb numerikus megoldását szeretnénk elérni. Az első módszerfejlesztések az 1930-as években kezdődtek, az áttörést azonban az informatikai háttér 1980-ban megindult – és máig tartó – rohamos fejlődése hozta el. Azóta a tudományterületen elért eredményeket két kémiai Nobel-díjjal is jutalmazták. Az elmúlt évtizeddel bezárólag az elsődleges cél a minél pontosabb módszerek kidolgozása és a bonyolult egyenletek automatikus implementálása volt. Sikeresen fejlesztettek ki olyan nagy pontosságú kvantumkémiai módszereket, amelyekkel a molekulák kísérletileg is mérhető fizikai és kémiai jellemzői (egyensúlyi szerkezet, elnyelési színképek, NMR-paraméterek) elméleti számítása lehetséges. Az így kapott eredmények pontossága összemérhető a mérési eredmények pontosságával, néhány esetben meg is haladhatják azt.
A több milliárd ismeretlen változót tartalmazó egyenletrendszerek megoldása azonban rendkívül számításigényes, bonyolultabb módszerek esetén a változók száma a rendszer méretének 7-8. hatványával skálázódik. Könnyű belátni, hogy az utóbbi esetben a vizsgált molekula méretének megkétszerezésével a számítási idő 256-szorosára nő, emiatt a legpontosabb módszerek alkalmazhatóságának felső határa csupán néhány atom. Ennek megfelelően az elmúlt években a módszerfejlesztések elsődleges célja a számítási idők csökkentése.
A kutatás célja, a megválaszolandó kérdések
Külső perturbáció, jellemzően elektromágneses sugárzás hatására az elektronszerkezet átrendeződik, és egy vagy több elektron gerjesztett állapotba kerül. Számos, napjainkban aktívan kutatott jelenség kapcsolódik az elektronszerkezet gerjesztett állapotához, mint például a fotokróm anyagok viselkedése, a fény által inicializált reakciók lejátszódása, illetve az energiaátadás és -tárolás. A gerjesztett állapotú tulajdonságok vizsgálata kvantumkémiai módszerekkel mára a kutatások rutinszerű eszközévé vált többek között a spektroszkópia [M4, M5], az analitika és a biokémia területén. Ennek megfelelően a modern kvantumkémia egyik legfontosabb feladata olyan megbízható és pontos módszerek kidolgozása, amelyekkel a gerjesztett állapotok elmélete alkalmazhatóságának felső határa a jelenlegi többszörösére kiterjeszthető, és számítások végezhetők akkora rendszerekre, amelyek jelenleg számításigényük miatt nem kezelhetők.
A kutatás célja olyan matematikai átalakítások kidolgozása, amelyekkel a számítások gyorsabban végezhetők el. Mint azt látni fogjuk, ezen átalakítások lehetnek csupán a számítási kapacitást és az informatikai hátteret jobban kihasználó megfontolások. Ebben az esetben a számításokhoz használt változók száma nem módosul, sőt akár nőhet is, azonban a hatékonyan programozható és futtatható algoritmusok miatt az egyenletek megoldása mégis kevesebb időt vesz igénybe (lásd. sűrűségillesztés). A matematikai transzformációk egy másik csoportjánál egy konkrét fizikai vagy kémiai kép által szabályozott átalakítást végzünk el; ebben az esetben hatékonyan csökkenthetjük a változók (például a molekulapályák) számát, ami a számítási idők drasztikus csökkenéséhez vezet (lásd: lokalizált molekulapályák). A végső cél a legmegfelelőbb átalakítások kidolgozása és kombinálása, illetve a változók számának minimalizálása addig, amíg az általunk bevezetett közelítések hibája átlagosan egy nagyságrenddel kisebb nem lesz, mint az alkalmazott módszer hibája.
Módszerek
Másodrendű algebrai diagramfelépítő [ADC(2)] módszer
Az algebrai diagramfelépítő (algebraic diagrammatic construction, ADC) elmélet egy tetszőleges pontosságú, hierarchikusan felépülő elektronkorrelációs módszercsalád gerjesztett állapotú tulajdonságok számítására. Az általunk használt módszer másodrendű gerjesztésekig veszi figyelembe a lehetséges elektronkonfigurációt [ADC(2)], így a számítások a molekulapályák számának ötödik hatványával skálázódnak [2].
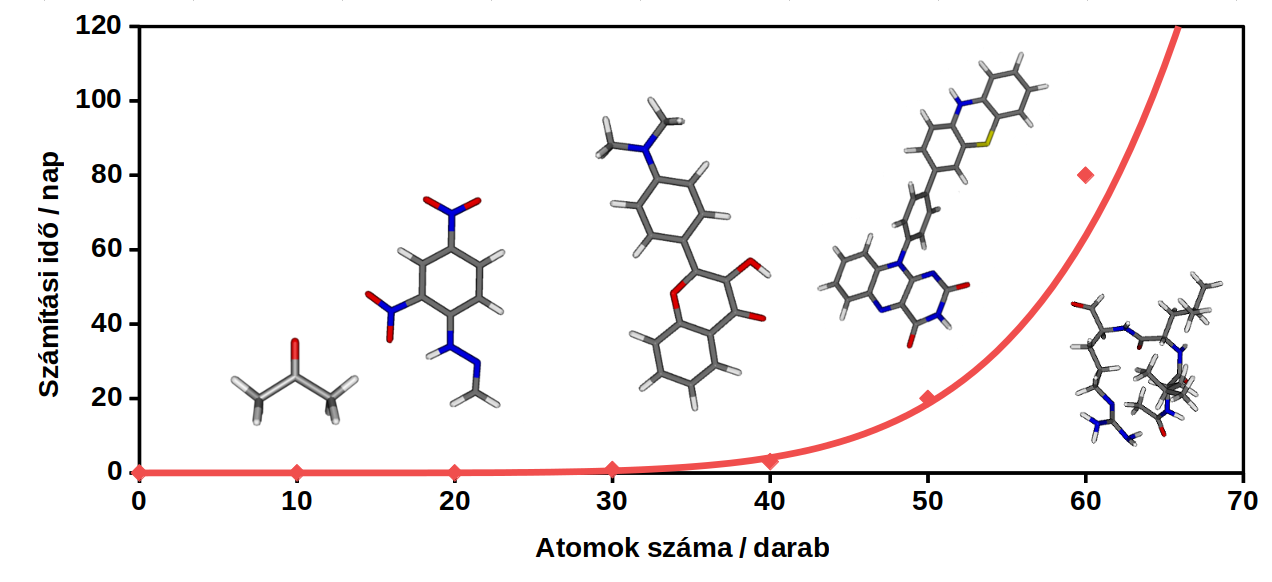
1. ábra: Az ADC(2) módszer esetén a számításokhoz hozzávetőlegesen szükséges idő az atomok számának függvényében
Az ADC(2) használata az utóbbi években terjedt el, miután bemutatták, hogy formalizmusa és pontossága megegyezik a legelterjedtebben használt másodrendű coupled-cluster (CC2) módszerével [3, 4]. Az ADC(2) nagy előnye az előbbivel szemben, hogy a számítások során egy Hermitikus sajátértékproblémát oldunk meg, tehát a mátrixegyenlet jobb és bal oldali sajátvektorai megegyeznek. A módszer hibája kísérleti eredményekhez viszonyítva átlagosan 0,2 - 0,3 eV [5].
Báziskészlet
A számításoknál az atompályák közelítésére ismert, azok alakját jól leíró, Gauss-típusú függvényeket használunk, és a molekulapályákat az atompályák lineáris kombinációjával állítjuk elő (LCAO-MO elmélet). Az általunk használt aug-cc-pVTZ báziskészlet [6] megfelelő pontosságú, bonyolult típusú gerjesztések (például Rydberg) számításához is.
Sűrűségillesztés (density fitting, DF)
A számítások során az elektronok közötti kölcsönhatást leíró kételektron-integrálokat hagyományosan négyindexes tömbökben tároljuk a számítógép memóriájában. Ezen tömbök mérete egy 50 atomot tartalmazó molekula esetén a fenti bázist alkalmazva a terrabájt nagyságrendbe esik, ami könnyen belátható, hogy nem tárolható a memóriában, így a számítások során minden egyes lépésben újra és újra fel kell olvasnunk a merevlemezről. A sűrűségillesztés [7] során ezen tömböket két, illetve háromindexes tömbök szorzataként közelítjük. Az így kapott tömbök mérete már „csak” néhány gigabájt, és így kényelmesen tárolhatók a memóriában. A mai korszerű számítógépek az egyes lépésekben sokkal gyorsabban számolják ki újra és újra az integrálok értékét az illesztéssel, mint amikor az előre kiszámolt integrálokat olvassák fel a merevlemezről.
Természetes pályák (natural orbital, NO)
A természetes pályákat az adott hullámfüggvényhez tartozó sűrűségmátrix diagonalizálásával állíthatjuk elő [8]. A diagonalizálás során kapott sajátvektorok a természetes pályák, a sajátértékek pedig megadják az adott pálya fontosságát az elektronkorreláció szempontjából. Bebizonyították, hogy a természetes pályák az adott szinten a molekulapályák legkompaktabb reprezentációi. Elterjedt eljárás, hogy egy kevésbé számításigényes módszerrel kapott természetes pályákból a sajátértékek szerint elhanyagolunk számos, kevésbé fontos pályát, és a pontos, számításigényes módszerhez már csak a legfontosabb pályákat használjuk fel, így csökkentve a molekulapályák és a változók számát. A kérdés az, hogy milyen módszerből érdemes a természetes pályákat származtatni, és meddig csökkenthető a pályák száma.
Lokalizált molekulapályák
Az elektronok közötti kölcsönhatás erőssége a részecskék közötti távolság hatodik hatványával csökken. Amennyiben az egész molekulára kiterjedt kanonikus molekulapályákat valamilyen algoritmus szerint, a kémiai intuíciót szem előtt tartva lokalizáljuk, a molekulán belül számos pálya közötti kölcsönhatás rendkívül kicsi lesz. Míg az egzakt számolásoknál minden járulékot ki kell számítanunk, addig a lokális közelítést alkalmazó számításoknál ezen integrálokat elhanyagolhatjuk, ezzel nagymértékben csökkentve a számítási időt, elhanyagolható mértékben csökkentve a pontosságot [9].
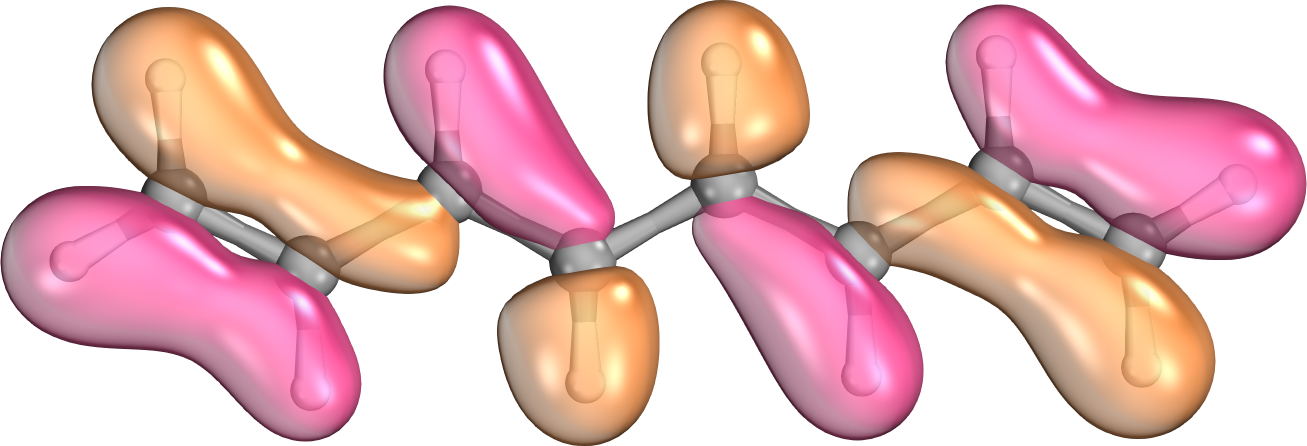
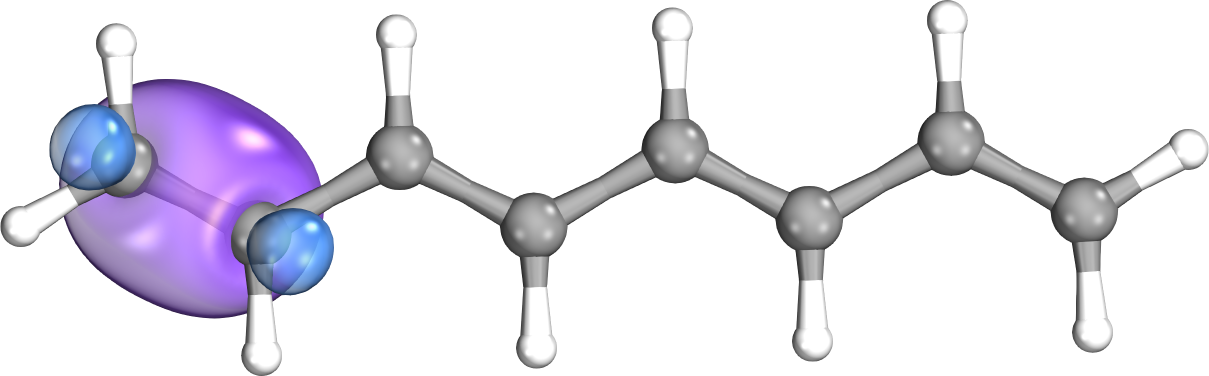
2. ábra: Az oktatetraén egy kanonikus (balra) és egy lokalizált (jobbra) molekulapályája
Eddigi eredmények
Sikeresen adtunk meg egy sűrűségmátrixot, amelyet felhasználva jó minőségű természetes pályák származtathatók gerjesztett állapotú számításokhoz. A sűrűségmátrix felírásának nehézségét az okozza, hogy a számítások során az alapállapotú egyenleteket is megoldjuk, és az azokból kapott átmeneti mennyiségeket is felhasználjuk a gerjesztett állapotú egyenletek megoldásához. Ebből következően a sűrűségmátrixnak egyszerre kell optimálisnak lennie az alap- és a gerjesztett állapotra is. A kapott eredmények alapján ideális egy úgynevezett állapotátlagolt sűrűségmátrix használata, ami az alapállapotra megfelelő másodrendű Møller-Plesset (MP2) és a gerjesztett állapotot leíró másodrendű perturbatív korrekciót tartalmazó konfigurációs kölcsönhatás [CIS(D)] módszerekből számított sűrűségmátrix átlaga. Az így kapott természetes pályák 60%-a elhanyagolható a számítások során, miközben a közelítésből származó átlagos hiba 0,02 eV.
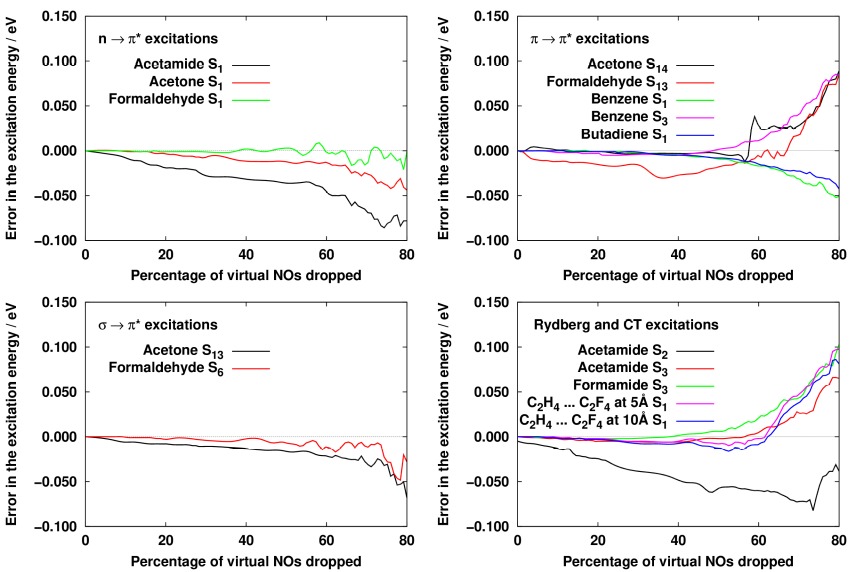
3. ábra: A gerjesztési energiákban kapott hiba az elhanyagolt molekulapályák számának függvényében
Továbbá elsőként alkalmaztuk gerjesztett állapotú számításokhoz a kutatócsoportunk által kifejlesztett, ún. „természetes kiegészítőfüggvények” közelítést. Az eljárás metodikailag nagyban hasonlít a természetes pályák számításához, azonban fizikai háttérrel nem rendelkezik. A módszer sikerességét a számítógépes képfeldolgozásból ismert példán keresztül lehet a legegyszerűbben megérteni. Ebben az esetben a sok pontot tartalmazó képen elvégzünk egy szingulárisérték-felbontást, amely szerint a képpontokat fontosságuk szerint sorba lehet rendezni. A kevésbé fontos pontokat elhanyagolva az emberi szem számára ugyanaz a kép jelenik meg, azonban jóval kisebb lesz a tárolt fájl mérete.


4. ábra: Míg a bal oldali kép (bmp) mérete 760 kilobájt, addig a jobb oldali kép (jpg) mérete 45 kilobájt
Esetünkben a képpontok a sűrűségillesztéshez használt kiegészítőfüggvények, ezek számát tudjuk nagymértékben csökkenteni, miközben az illesztett integrálok minősége hasonló az eredetihez. A közelítés gyakorlatilag hibamentes, és ha figyelembe vesszük, hogy a természetes pályák csökkentésével már csak 60%-kal kevesebb molekulapályát kell pontosan illesztenünk, összességében a függvények száma 80%-kal csökkenthető. Nagy molekulákra végzett számítások eredményei alapján elmondhatjuk, hogy az egyenletek 35-ször gyorsabban oldhatók meg, illetve 35-ször kisebb memória szükséges, mint az egzakt számítások esetén. Értelemszerűen a természetes pályák és kiegészítőfüggvények előállítása többletszámolást eredményez, de a teljes sebességgyorsulás még így is átlagosan 15-szörös [M1, M2]. A kifejlesztett módszer sikeresen alkalmazható molekulák elnyelési színképének elméleti úton történő meghatározására az ultraibolya-látható (UV-VIS) tartományban,
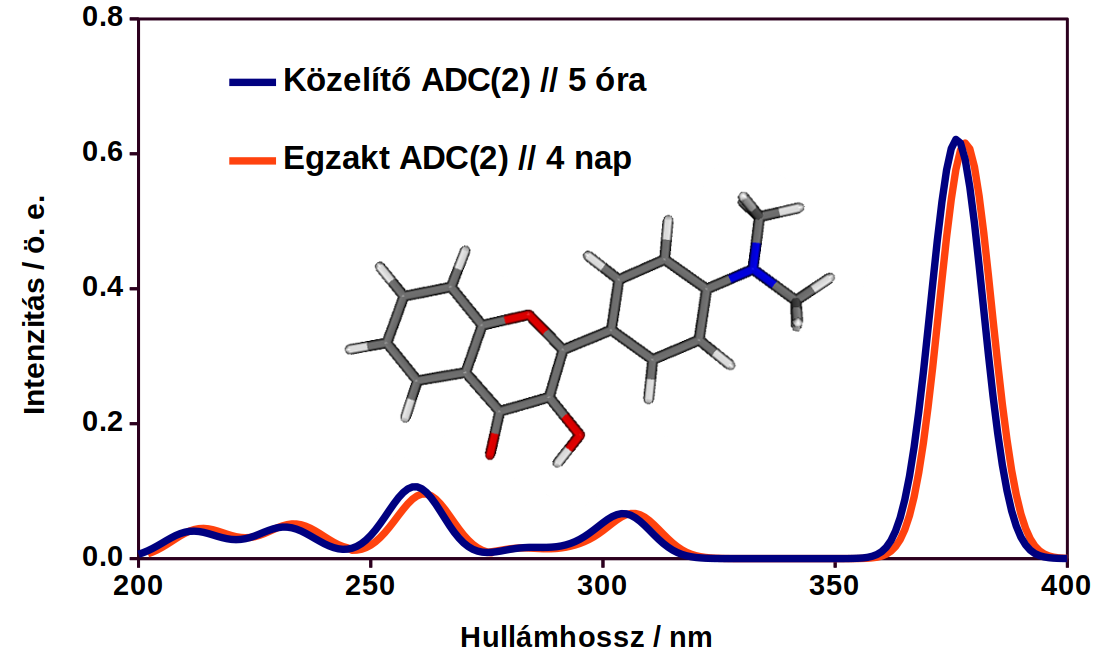
5. ábra: Egy flavon-származék UV-VIS spektruma az egzakt és a közelítő módszerrel
illetve a közelítéseknek köszönhetően rutinszerűen számíthatók 100 atomot meghaladó molekuláris rendszerek.
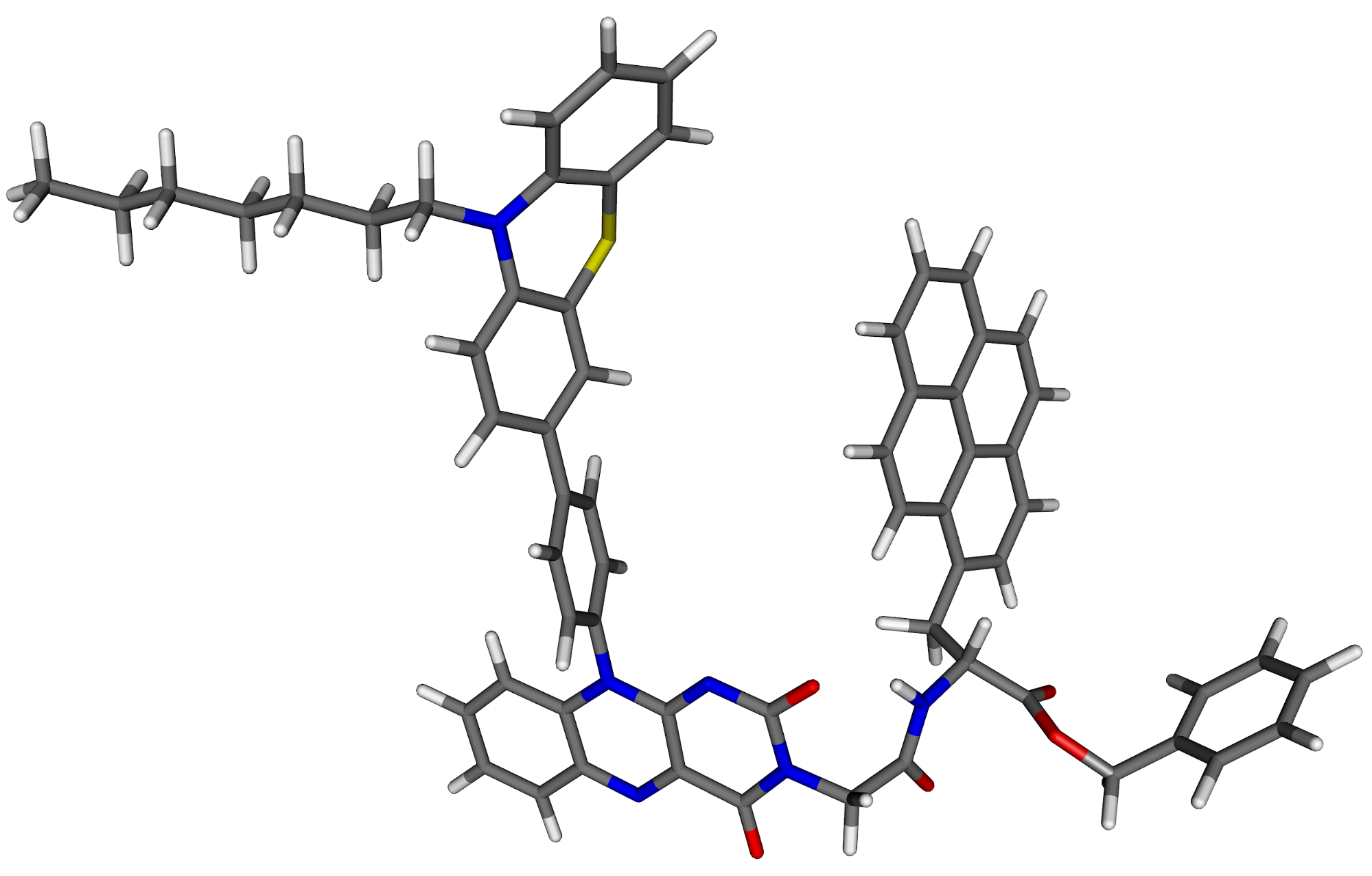
6. ábra: Az általunk kiszámolt, 127 atomot tartalmazó szerves festék szerkezete
Jelenlegi kutatásaink során a lokális közelítések kombinálását vizsgáljuk a fent bemutatott közelítésekkel [M3]. Ebben az esetben elsőként egy alacsonyabb rendű (például CIS) módszer segítségével meghatározzuk a gerjesztésben részt vevő molekulapályákat. Ezen pályákat kiegészítjük további, lokalizációs kritériumok alapján (molekulapályák közötti távolság és kölcsönhatás nagysága) kiválasztott pályákkal, és kizárólag az így definiált altérben végezzük el a pontos számításokat. A kapott altér mérete jelentősen kisebb, mint a teljes molekula. Előzetes eredményeink alapján elmondhatjuk, hogy a vizsgált rendszerekre további 3-szoros (az egzakt módszerhez képest 45-szörös) sebességgyorsulást értünk el, míg a teljes eljárás átlagos hibája 0,03 eV, tehát továbbra is egy nagyságrenddel kisebb, mint az eredeti módszer hibája. Ennek köszönhetően tovább csökkenthetők a számítási idők, illetve növelhető a vizsgált rendszerek mérete.
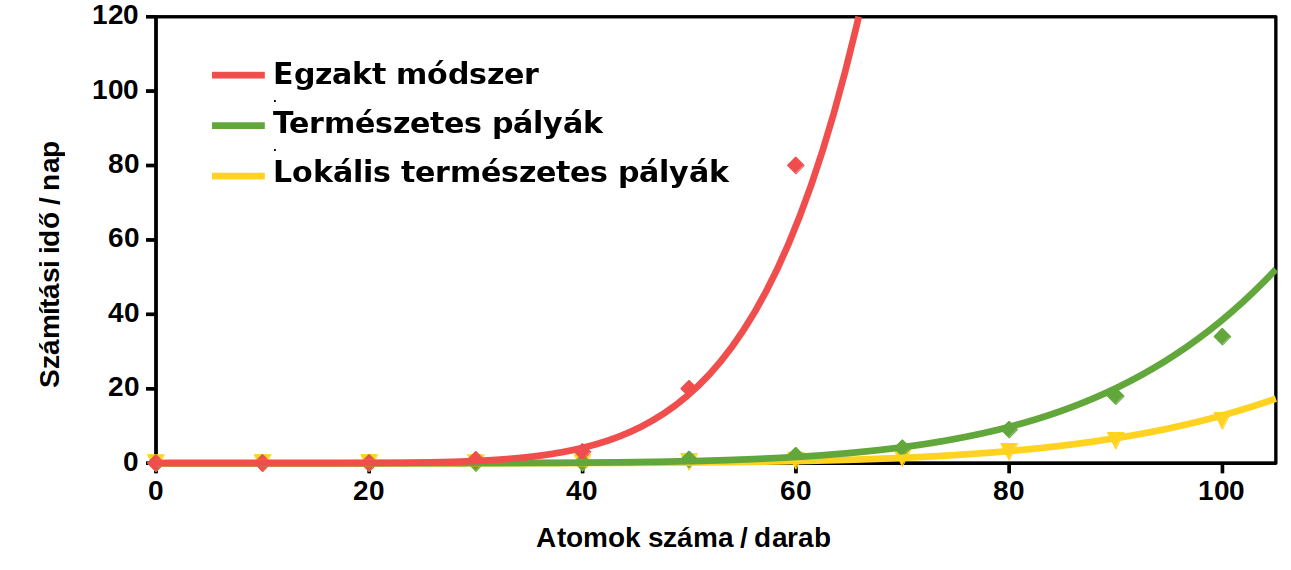
7. ábra: A számítások hozzávetőleges időigénye az egyes közelítéseknél
Várható impakt, további kutatás
További céljaink között szerepel a lokális közelítések során alkalmazott algoritmus véglegesítése, illetve további számítások elvégzése. Várhatóan a végső algoritmussal az alterek mérete tovább csökkenthető, illetve pontos számításokat végezhetünk több száz atomos rendszerekre.
Az általunk kifejlesztett közelítések implementációja tudományos célokra ingyenesen elérhető a kutatócsoportunk által fejlesztett Mrcc programcsomagban [M6], amelyet több százan használnak világszerte. Az általam készített program alkalmazható a szerves, a biomolekuláris és a fotokémia területén gerjesztési energiák és abszorpciós, cirkuláris dikroizmus-spektrumok meghatározására, illetve a gerjesztésben részt vevő molekulapályák és a töltéseloszlás változásának vizsgálatára. Az elméletet már több kutatócsoport felhasználta, illetve implementálta saját programjának fejlesztői verziójában. Az elkészített keretrendszer kiindulópontja lehet számos további módszerfejlesztésnek, amelyek a programban végzett apróbb módosítások után tesztelhetők, illetve alkalmazhatók.
Saját publikációk, hivatkozások, linkgyűjtemény
Kapcsolódó saját hivatkozások:
[M1]: D. Mester, P. R. Nagy, és M. Kállay, J. Chem. Phys., 148, p. 094111, 2018. (IF: 2.965)
[M2]: D. Mester, P. R. Nagy, és M. Kállay, J. Chem. Phys., 146, p. 194102, 2017. (IF: 2.965)
[M3]: D. Mester, P. R. Nagy, and M. Kállay, előkészületben.
[M4]: D. Hessz, M. Bojtár, D. Mester, Z. Szakács, I. Bitter, M. Kállay, és M. Kubinyi, Spectrochimica Acta Part A, 203, p. 96, 2018. (IF: 2.536)
[M5]: P. Bagi, K. Juhász, I. Tímári, K. E. Kövér, D. Mester, M. Kállay, M. Kubinyi, T. Szilvási, P. Pongrácz, L. Kollár, K. Karaghiosoff, M. Czugler, L. Drahos, E. Fogassy, és G. Keglevich, J Organom. Chem., 797, p. 140, 2015. (IF: 2.336)
[M6]: Mrcc, a quantum chemical program suite written by M. Kállay, Z. Rolik, J. Csontos, P. Nagy, G. Samu, D. Mester, J. Csóka, B. Szabó, I. Ladjánszki, L. Szegedy, B. Ladóczki, K. Petrov, M. Farkas, P. D. Mezei, és B. Hégely.
Egyéb saját hivatkozások:
[M7]: M. Bojtár, P. Z. Janzsó-Berend, D. Mester, D. Hessz, M. Kállay, M. Kubinyi, és I. Bitter, Beilstein J. Org. Chem., 14, p. 747, 2018. (IF: 2.337)
[M8]: J. Hári, P. Polyák, D. Mester, M. Micusik, M. Omastova, M. Kállay, és B. Pukánszky, App. Clay Sci., 132–133, p. 167, 2016. (IF: 3.101)
[M9]: D. Mester, J. Csontos, és M. Kállay, Theoretical Chemistry Accounts, 134, p. 74, 2015. (IF: 1.806)
Linkgyűjtemény:
Kémiai Nobel-díjak a kvantumkémia területén: 1, 2
Hivatkozások:
[1]: P. R. Nagy, G. Samu, és M. Kállay, J. Chem. Theory Comput., 12, p. 4897, 2016.
[2]: J. Schirmer, Phys. Rev. A, 26, p. 2395, 1982.
[3]: C. Hättig, Adv. Quant. Chem., 50, p. 37, 2005.
[4]: O. Christiansen, H. Koch, and P. Jørgensen, Chem. Phys. Lett., 243, p. 409, 1995.
[5]: O. Christiansen, H. Koch, P. Jørgensen, and J. Olsen, Chem. Phys. Lett., 256, p. 185, 1996.
[6]: T. H. Dunning Jr., J. Chem. Phys., 90, p. 1007, 1989.
[7]: S. F. Boys, G. B. Cook, C. M. Reeves, and I. Shavitt, Nature, 178, p. 1207, 1956.
[8]: W. Meyer, J. Chem. Phys., 58, p. 1017, 1973.
[9]: P. Pulay, Chem. Phys. Lett., 100, p. 151, 1983.
