Pattantyús-Ábrahám Géza Gépészeti Tudományok Doktori Iskola 

BME Gépészmérnöki Kar, Gép-és Terméktervezés Tanszék

Témavezető: Dr. Kerényi György

Kukorica növény diszkrét elemes modellezése

A kutatási téma néhány soros bemutatása

Bolygónk népességének növekedésével párhuzamosan civilizációnk is rohamosan fejlődik. Ebből adódóan egyre nagyobb mennyiségű és egyre jobb minőségű élelmiszerre van szükségünk, amelynek megtermeléséhez nélkülözhetetlenek a nagyobb teljesítményű és jobb hatásfokú mezőgazdasági gépek (1. ábra).

A mezőgazdasági gépek fejlesztésének általános gyakorlata az új konstrukciók megépítése és valós körülmények közötti tesztelése („trial and error” módszer). E módszer alkalmazása a termények idényjellege miatt időben és térben is korlátozott, továbbá rendszerint jelentős a költségvonzata is.

Napjainkban az általános gépészeti fejlesztésben teljesen általánosnak számít az új konstrukciók numerikus analízise a virtuális térben, ami csökkenti a prototípus fejlesztés költségeit és bővíti az elérhető mérési és megfigyelési lehetőségeket. Ezzel szemben a mezőgazdasági gépek területén még nem alakult ki olyan fejlesztési eljárás, amely alkalmas lenne a termények és a velük kapcsolatba lépő berendezések kölcsönhatásainak modellezésére.

Ezért a PhD kutatásom keretében egy olyan numerikus módszer fejlesztésén dolgozom, amely alkalmas szálas mezőgazdasági anyagok és a velük kapcsolatba lépő berendezések kölcsönhatásának modellezésére. A kutatás során egy speciális termény, a kukoricanövény és egy speciális folyamat, a betakarítás elemzésén keresztül igazolom a választott numerikus módszer, a diszkrét elemek módszerének alkalmazhatóságát.

 

1. ábra: Gabonabetakarítás a középkorban (balról) és napjainkban (jobbról) [L1,L2]

 

A kutatóhely rövid bemutatása

Kutatásomat a Budapesti Műszaki és Gazdaságtudományi Egyetem (BME), Gépészmérnöki Karának (GPK), Gép-és Terméktervezés Tanszékén végzem (GT3), ahol komoly hagyománya van a mezőgazdasági géptervezéssel kapcsolatos oktatásnak és kutatásnak. Ipari partnereinkhez hasonlóan kutatócsoportunk is egyre nagyobb hangsúlyt fektetett a mezőgazdasági gépek és folyamatok numerikus modellezésére az elmúlt években.

A kutatás történetének, tágabb kontextusának bemutatása

Az informatika rohamos fejlődése az elmúlt években lehetőséget adott az összetett és nagy számítási kapacitást igénylő folyamatok elemzésére. Ezzel párhuzamosan újabbnál- újabb numerikus módszerek alakultak ki, amelyek közül a diszkrét elemek módszerét (DEM) kezdték el szélesebb körben is alkalmazni mezőgazdasági anyagok modellezésére [1].

A DEM jellegéből adódóan először szemcsés mezőgazdasági anyagok, talaj és szemes termények, illetve a hozzájuk kapcsolódó technológiai folyamatok elemzését végezték: talajművelés [2], silók ürítése [3], szemek szárítása [4], cséplés folyamata [5].

Szálas mezőgazdasági és erdészeti anyagok diszkrét elemes modellezésével kapcsolatban kevesebb anyag található. Több, szálas anyagok modellezésére alkalmas DEM geometriai modellt (gömbsormodell, kiegészített gömbsormodell, membrán- és tömör modell) definiált Jünemann et al. [6]. Gabonaszárak nyomó és hajlító igénybevétellel szembeni ellenállásának modellezésére fejlesztett modellt Leblicq et al. [7, 8]. A fűszálak és a fűkasza kapcsolatát, a vágási energia hatékonyságát és a vágás minőségét vizsgálta a betakarítási folyamat során Kemper et al. [9]. Cotzee és Lombard szőlőszemek leválasztási és válogatási folyamatát vizsgálta [10]. Fás szárak ütésszerű igénybevétellel szembeni ellenállását tanulmányozta Olmedo et al. [11].

Jól látható, hogy a korábbi kutatások során létrehozott modellek és az ezek hitelesítéséhez elvégzett mérések a termények egy tipikus mechanikai tulajdonságára fókuszálnak, habár a valós folyamatok során szinte minden esetben összetett mechanikai igénybevételnek vannak kitéve.

A kutatás célja, a megválaszolandó kérdések.

A kutatásom fő célja létrehozni egy olyan diszkrét elemes modellt a betakarításra érett kukoricanövényről, amely alkalmas a betakarítás során fellépő összetett folyamatok és igénybevételek mennyiségi és minőségi elemzésére, ezáltal támogatva a kukorica betakarításához kapcsolódó berendezések fejlesztését.

A kutatás során az alábbi hipotéziseket szeretném igazolni a kukoricanövényt, illetve a diszkrét elemes modellt illetően:

●     létrehozható egy mérési folyamat, amely megfelelő mennyiségű és minőségű információt nyújt a kukoricanövény feldolgozási folyamatát befolyásoló jelenségekről;

●     egyértelmű összefüggés található a kukoricanövény morfológiai és fizikai tulajdonságai között;

●     egyértelmű összefüggés található a kukoricanövényt alkotó morfológiai elemek fizikai tulajdonságai és a morfológiai elem mechanikai viselkedése között;

●     a diszkrét elemek módszere alkalmas a kukoricanövény fizikai és mechanikai modelljének megalkotására;

●     létrehozható egy kalibrálási folyamat, amely alkalmas a modell fizikai és mechanikai paramétereinek meghatározására;

●     egyértelműen meghatározhatók azok a modellparaméterek, amelyek jelentősen befolyásolják a modell mechanikai viselkedését;

●     a hitelesített diszkrét elemes modell alkalmas a kukoricanövény feldolgozási folyamatának szimulációjára;

●     a folyamat szimulációs eredményei felhasználhatóak a berendezések tervezése során.

Módszerek

Egy összetett mérési módszert dolgoztam ki a kukoricanövény fizikai és mechanikai állapotának elemzésére, az ehhez kapcsolódó hipotézisek igazolására, amely a következő méréseket és megfigyeléseket foglalja magában [K1, K2]:

●     a kísérleti területre jellemző talajösszetétel meghatározása;

●     a kísérleti területre jellemző meteorológiai paraméterek (napi átlaghőmérséklet, csapadékmennyiség, napsütéses órák száma) meghatározása;

●     a növényt jellemző geometriai méretek mérése;

●     a növényt jellemző fizikai paraméterek (nedvességtartalom, tömeg) mérése;

●     a növényt alkotó különböző morfológiai elemek befogott hajlító vizsgálata;

●     a növényt alkotó különböző morfológiai elemek hárompontos hajlító vizsgálata;

●     a növényt alkotó különböző morfológiai elemek négypontos hajlító vizsgálata;

●     a növényt alkotó különböző morfológiai elemek szakaszos oldalirányú nyomóvizsgálata;

●     a növényt alkotó különböző morfológiai elemek lokális oldalirányú nyomóvizsgálata;

●     a növényt alkotó különböző morfológiai elemek dinamikus vágómunka-vizsgálata, ép száron és nyomott száron;

●     a növényt alkotó szártagok egytengelyű húzóvizsgálata;

●     a betakarításra érett növény termésének leválasztásához szükséges erő mérése;

●     a betakarításra érett növény termése ütközési együtthatójának mérése különböző felületeken;

●     betakarításhoz kapcsolódó megfigyelések elvégzése.

2. ábra: Kukoricanövény fő fizikai és mechanikai jellemzőinek meghatározása:

a) kukoricacső helyzete; b) szártagok nedvességtartalma; c) szártagok tömege; d) szártagok keresztmetszete; e) kukoricacső leválasztásához szükséges erő; f) kukoricacsövek hossza; g) kukoricacsövek tömege; h) kukoricacsövek átmérője; i) kukoricacsövek alakja; j) szártagszakaszok oldalirányú összenyomása; k) szártagok lokális oldalirányú összenyomása; l) szártagok dinamikus vágása; m) szártagok egytengelyű húzása; n) szártagok hárompontos hajlítása; o) szártagok négypontos hajlítása; p) szárszakasz befogott hajlítása [K1, K2]

 

A mérések és megfigyelések során szerzett tapasztalatok alapján létrehoztam a kukoricanövény diszkrét elemes modelljét, amely magában foglalja a növény idealizált gyökérzetét, szárát és egy kukoricacsövet. Ahhoz, hogy a különböző morfológiai elemek modellparamétereit és kapcsolatait be tudjuk állítani, kiterjedt paraméteranalízist végeztem a negyedik szártag modelljén (3. ábra) az oldalirányú nyomás, hárompontos hajlítás és dinamikus vágás kísérleteit felhasználva. [K3, K4, K5]

 

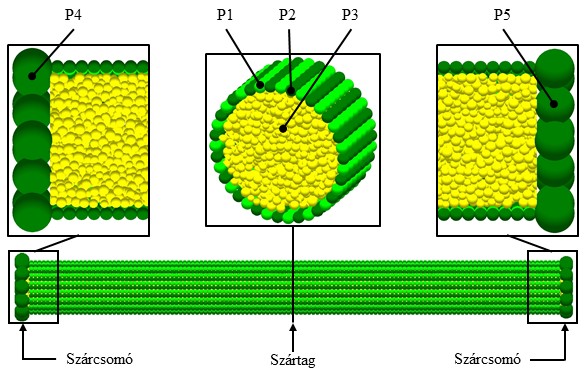
3. ábra: A negyedik szártag diszkrét elemes modellje, amelyet a következő elemek építenek fel: szárfalban P1 és P2; szárbélben P3; szárcsomóban P4 és P5

 

Ahhoz, hogy a modell megfelelő pontossággal képes legyen megjósolni a kölcsönhatást a növény és a gép között összetett igénybevétel esetén, egy paraméterkalibrálási eljárást dolgoztam ki az elvégzett kísérleteket felhasználva, 4. ábra. [K6, K7, K8]

 

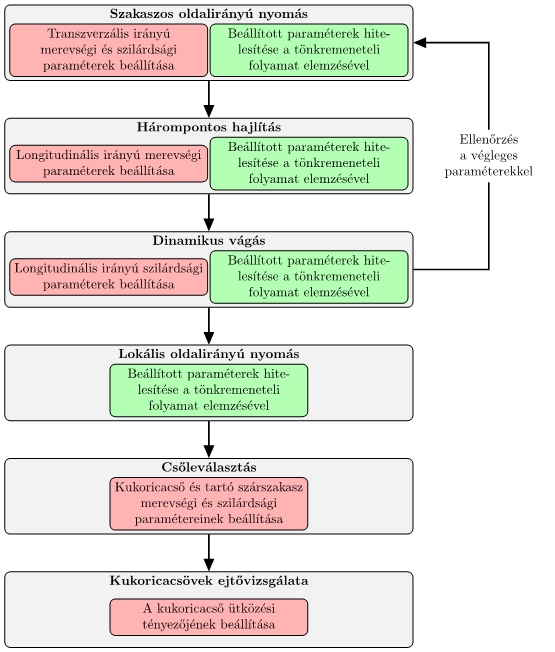
4. ábra: A DEM-modell paramétereinek kalibrálási és hitelesítési eljárása [K6]

 

A kutatás utolsó lépésében a kalibrált és hitelesített diszkrét elemes kukoricanövény-modell, valamint egy kukoricaadapter számítógépes modelljének (5. ábra) segítségével létrehozott virtuális környezetben technológiai szimuláció elvégzése a cél. [K9, K10]

 

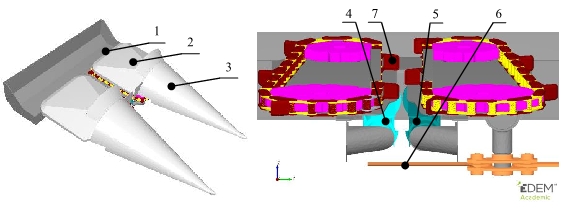
5. ábra: Kukoricaadapter számítógépes modellje:

1: csőgyűjtő; 2: burkolati elem; 3: sorterelő; 4-5: jobb és bal lehúzóhenger; 6: szecskázó egység; 7: behúzó láncok [K9]

 

Eddigi eredmények

A mérések és megfigyelések során számos, korábban még nem mért fizikai, morfológiai és mechanikai jellemzőt, valamint mechanikai viselkedést határoztam meg. Ezek a közül a legfontosabbak [K1, K2]:

●     a kukoricaszár egyenértékű keresztmetszeti mérete bilineáris csökkenést mutat a szártőtől a tízedik szártagig, amelyen a töréspont a hatodik szártag magassága, ahol a termés helyezkedik el;

●     az első öt szártag nedves tömege teszi ki a vizsgált teljes tömeg ~85%-át, így ezek a részek adják a szecskázott biomassza jelentős részét;

●     képfeldolgozási módszerek segítségével meghatároztam egy „ideális” termés tengelyszimmetrikus alakját és tömegközéppontját;

●     meghatároztam minden egyes vizsgált szártag oldalirányú összenyomásához, hajlításához és vágásához szükséges munkát, amely minden esetben csökkenő tendenciát mutatott a szártőtől a tízedik szártagig úgy, hogy az első öt szártag adta a szükséges teljes munka ~80%-át;

●     meghatároztam az oldalirányú nyomás, hajlítás és vágás során fellépő jellemző tönkremeneteli módokat;

●     meghatároztam a termés leválasztásához szükséges erőt;

●     meghatároztam a termés ütközési tényezőjét különböző felületekkel történő ütközés során.

A modell mechanikai viselkedésére a különböző terhelési esetek során jelentős hatással lévő modellparaméterek meghatározásához egy alapos paraméteranalízisnek vetettem alá a virtuális növény negyedik szártagját. A paraméteranalízis fontosabb eredményeit a 6. ábra foglalja össze. [K3, K4, K5, K6]

 

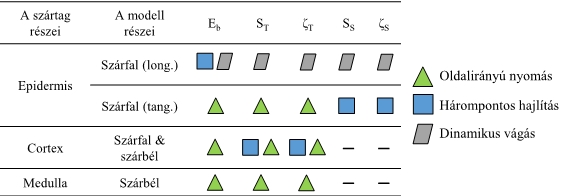
6. ábra: Paraméterek kapcsolata a terhelési esetekkel:

E_b: kapcsolat merevsége; S_T: kapcsolat húzószilárdsága; ζ_T: húzószilárdság variációs tényezője; S_S: kapcsolat nyírószilárdsága; ζ_S: nyírószilárdság variációs tényezője

 

A paraméteranalízis eredményeit, valamint a kalibrálási és hitelesítési eljárást felhasználva meghatároztam a paraméterek azon kombinációját, amellyel a modell a lehető legjobban megközelítheti a valós szártag mechanikai viselkedését különböző terhelési esetek során.

A 7. ábra mutatja az oldalirányú nyomás kísérleti és numerikus eredményeit. Jól látható, hogy a virtuális modell válasza a nyomó igénybevétel során szinte azonos a kísérlet útján meghatározott jelleggel. Továbbá, a virtuális szártag tönkremeneteli jellege, a repedések és törések kialakulása is nagyon hasonló a kísérlet során tapasztaltakhoz. [K4, K5, K6]

 

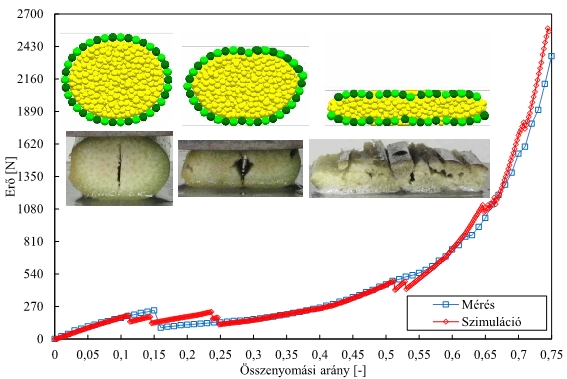
7. ábra: Oldalirányú nyomás kísérleti és numerikus eredményei [K6]

 

A 8. ábra mutatja a hárompontos hajlítás kísérleti és numerikus eredményeit. Jól látható, hogy a virtuális modell válasza a hajlító igénybevétel során szinte azonos a kísérlet útján meghatározott jelleggel, kivéve az utolsó szakaszban, amelynek oka az alkalmazott kapcsolati modell elasztikus mivolta. Továbbá, a virtuális szártag tönkremeneteli jellege, a repedések és törések kialakulása is nagyon hasonló a kísérlet során tapasztaltakhoz. [K4, K5, K6]

 

8. ábra: Hárompontos hajlítás kísérleti és numerikus eredményei [K6]

 

A 9. ábrán láthatók a dinamikus vágás kísérleti és numerikus eredményei. A numerikus vágás során ugyanazok a jelenségek azonosíthatók, mint a valós folyamat során: kezdeti összenyomás, vágás és csúszás. Továbbá, a virtuális szártag vágási felülete nagyon hasonló a kísérletek során tapasztaltakhoz. [K4, K5, K6]

 

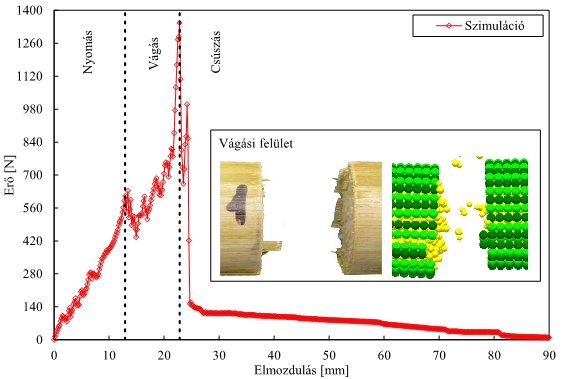
9. ábra: Dinamikus vágás kísérleti és numerikus eredményei [K6]

 

Várható impakt, további kutatás

A kidolgozott és elvégzett mérési eljárással a kukoricanövény számos olyan fizikai, fiziológiai és mechanikai tulajdonságát határoztam meg, amelyeket korábban nem, vagy csak korlátozottan mértek a kutatók. A mérési eredmények nem csak egy virtuális modell létrehozásához, hanem fajtakísérletekhez és tenyésztéshez is felhasználhatók.

Az általam készített modell alkalmas a kukoricanövény és a kukoricaadapter betakarítás során fellépő interakciójának elemzésére. A kukoricaszár-modell képes megjósolni a szár mechanikai viselkedését különböző terhelési esetek során.

A további vizsgálatok során a teljes növény modelljére fogok koncentrálni. A paraméteranalízis és a kalibrálási eljárás segítségével létrehozom a kukoricaszár eddig nem vizsgált részeit, valamint a szár és a termés kapcsolatát. Végül elvégzem a technológiai szimulációt, és elemzem a növény és a gép kapcsolatát.

Saját publikációk, hivatkozások, linkgyűjtemény

Kapcsolódó saját publikációk listája:

 

[K1] Kovács, Á., Jóri, I.J., Gaál, K., Piros, A., Kerényi, G., 2015. Development of measurement methods for a numerical simulation of corn plants. Mechanical Engineering Letters, Szent István Egyetem, 13, 88–96.

 

[K2] Kovács, Á., Jóri I.J., Kerényi G., Gaál K., 2015. Mérési módszerek kifejlesztése kukorica növény numerikus szimulációjához. Mezőgazdasági Technika, LVI. évf. (12) 2–5.

 

[K3] Kovács, Á., Kerényi, G., 2016. Comparative analysis of different geometrical structures of discrete element method (DEM) for fibrous agricultural materials. 4th CIGR International Conference of Agricultural Engineering (CIGR-AgEng2016). Aarhus, Dánia.

 

[K4] Kovács, Á., Kotrocz, K., Kerényi, G., 2015. The adaptability of discrete element method (DEM) in agricultural machine design. Hungarian Agricultural Engineering, 27, 14–19. https://doi.org/10.17676/HAE.2015.27.14

 

[K5] Kovács, Á., Kerényi, G., 2016. Stochastic variation in discrete element method (DEM) for agricultural simulations. Hungarian Agricultural Engineering, 30, 31–38. https://doi.org/10.17676/HAE.2016.30.31

 

[K6] Kovács, Á., Kerényi, G., 2018. A new method to calibrate discrete element models of fibrous agricultural materials. European Agricultural Engineering Conference (AgEng 2018). Wageningen, Hollandia, 2018. július 8–12.

 

[K7] Kovács, Á., Rádics, P. J., Kerényi, G., 2017. A discrete element model for agricultural decision support. 31st European Conference on Modelling and Simulation (ECMS 2017). Budapest, Magyarország, 2017. május 23–26.

 

[K8] Kovács, Á., Kerényi, G., 2017. Modeling of corn ears by discrete element method (DEM). 31st European Conference on Modelling and Simulation (ECMS 2017). Budapest, Magyarország, 2017. május 23–26.

 

[K9] Kovács, Á., Zwierczyk, P.T., 2018. Coupled DEM-FEM simulation on maize harvesting. 32nd European Conference on Modelling and Simulation (ECMS 2018). Wilhelmshaven, Németország, 2018. május 22–25.

 

[K10] Kovács, Á., Zwierczyk, P.T., Kerényi, G., 2017. Kapcsolt véges és diszkrét elemes szimulációk (FEA-DEM) alkalmazása a mezőgazdasági géptervezésben. XXV. Nemzetközi Gépészeti Találkozó, ISSN 2068-1267. Kolozsvár, Románia, 2017.

 

Linkgyűjtemény:

 

[L1] Gabonabetakarítás a középkorban

 

[L2] Gabonabetakarítás napjainkban

 

Hivatkozások listája:

 

[1] Cundall, P.A., Strack, O.D.L., 1979. A discrete numerical model for granular assemblies. Géotechnique 29, 47–65. https://doi.org/10.1680/geot.1979.29.1.47

 

[2] Tamás, K., Jóri, I.J., Mouazen, A.M., 2013. Modelling soil-sweep interaction with discrete element method. Soil and Tillage Research 134, 223–231. https://doi.org/10.1016/j.still.2013.09.001

 

[3] Coetzee, C.J., Els, D.N.J., 2009. Calibration of discrete element parameters and the modelling of silo discharge and bucket filling. Computers and Electronics in Agriculture 65, 198-212. https://doi.org/10.1016/j.compag.2008.10.002

 

[4] Keppler, I., Kocsis, L., Oldal, I., Farkas, I., Csatar, A., 2012. Grain velocity distribution in a mixed flow dryer. Advanced Powder Technology 23, 824–832. https://doi.org/10.1016/j.apt.2011.11.003

 

[5] Yu, Y., Fu, H., Yu, J., 2015. DEM-based simulation of the corn threshing process. Advanced Powder Technology 26, 1400–1409. https://doi.org/10.1016/j.apt.2015.07.015

 

[6] Jünemann, D., Kemper, S., Frerichs, L., 2013. Simulation of stalks in agricultural processes – Applications of the Discrete Element Method. Landtechnik 68, 164–167.

 

[7] Leblicq, T., Smeets, B., Ramon, H., Saeys, W., 2016. A discrete element approach for modelling the compression of crop stems. Computers and Electronics in Agriculture 123, 80–88. https://doi.org/10.1016/j.compag.2016.02.018

 

[8] Leblicq, T., Smeets, B., Vanmaercke, S., Ramon, H., Saeys, W., 2016. A discrete element approach for modelling bendable crop stems. Computers and Electronics in Agriculture 124, 141–149. https://doi.org/10.1016/j.compag.2016.03.022

 

[9] Kemper, S., Thorsten, L., Frerichs, L., 2014. The overlaid cut in a disc mower – results from field tests and simulation. Landtechnik 69, 171–175.

 

[10] Coetzee, C.J., Lombard, S.G., 2013. The destemming of grapes: Experiments and discrete element modelling. Biosystems Engineering 114, 232–248. https://doi.org/10.1016/j.biosystemseng.2012.12.014

 

[11] Olmedo, I., Bourrier, F., Bertrand, D., Berger, F., Limam, A., 2016. Discrete element model of the dynamic response of fresh wood stems to impact. Engineering Structures 120, 13–22. https://doi.org/10.1016/j.engstruct.2016.03.025