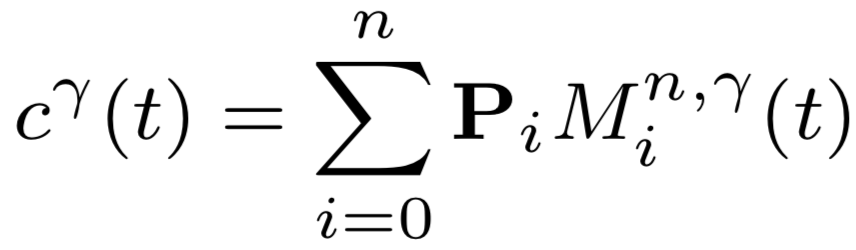BME Informatikai Tudományok Doktori iskola 

BME VIK, Irányítástechnika és Informatika Tanszék

Témavezető: Dr. Várady Tamás

P-görbék és felületek ─ új reprezentációk a geometriai modellezésben 

A kutatási téma néhány soros bemutatása

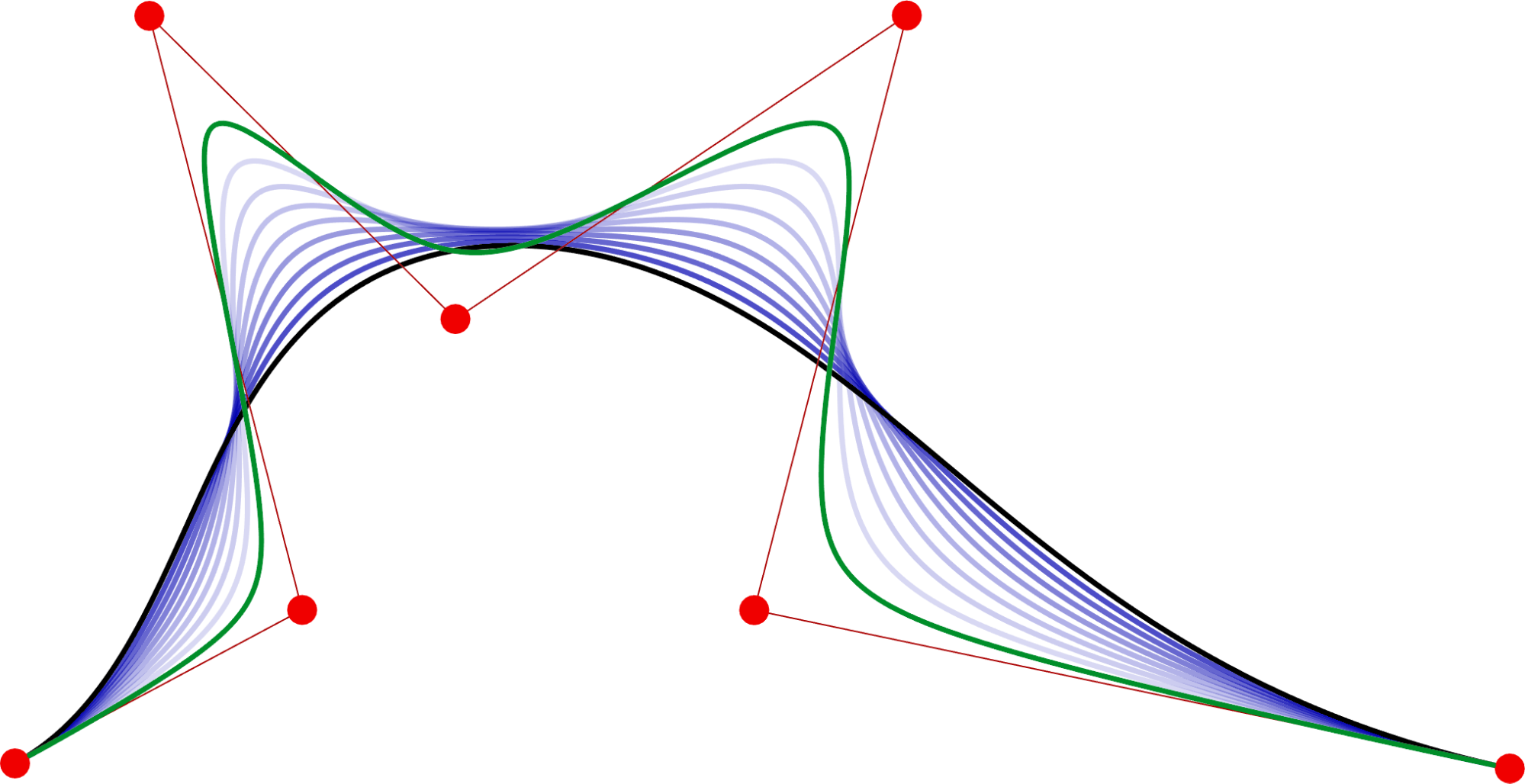
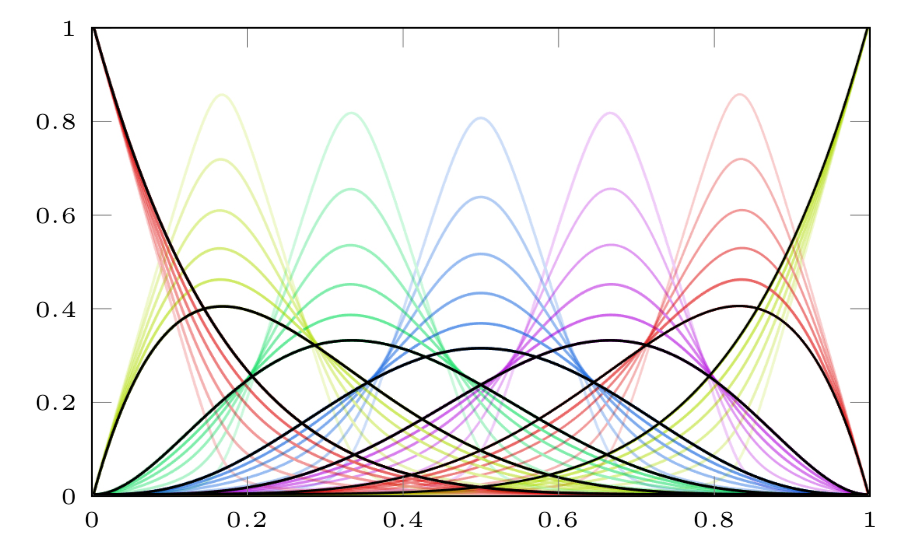
A számítógéppel segített geometriai tervezésben (CAD) a kontrollpontokkal megadott szabadformájú görbék és felületek nagyon fontos szerepet játszanak. A legelterjedtebb reprezentációk a Bézier és B-spline görbék és felületek, amelyeket szinte minden CAD rendszerben megtalálhatunk. Bár a szabványos reprezentációk elmélete nagyon régi és kiforrott [1], a mai napig aktívan keresnek új reprezentációkat, amelyek esetleg kiválthatják vagy kiegészíthetik a klasszikus reprezentációkat. Az általunk kidolgozott ún. proximity (kontrollpoligonhoz való közelséget szabályozó) görbe  egy adott kontrollpoligonhoz egy folytonos paraméterrel megadott görbecsaládot definiál, ahol a paraméter szabályozza, hogy a kontrollpontok milyen erősen befolyásolják a görbék alakját; ugyanakkor a klasszikus reprezentációk számos előnyös tulajdonságát megőrzi. Lásd 1. ábra, illetve az általunk kidolgozott internetes keretrendszer.

 

 

1. ábra: P-Bézier görbék és a hozzájuk tartozó bázisfüggvények, különböző proximity paraméterekkel.

A kutatóhely rövid bemutatása

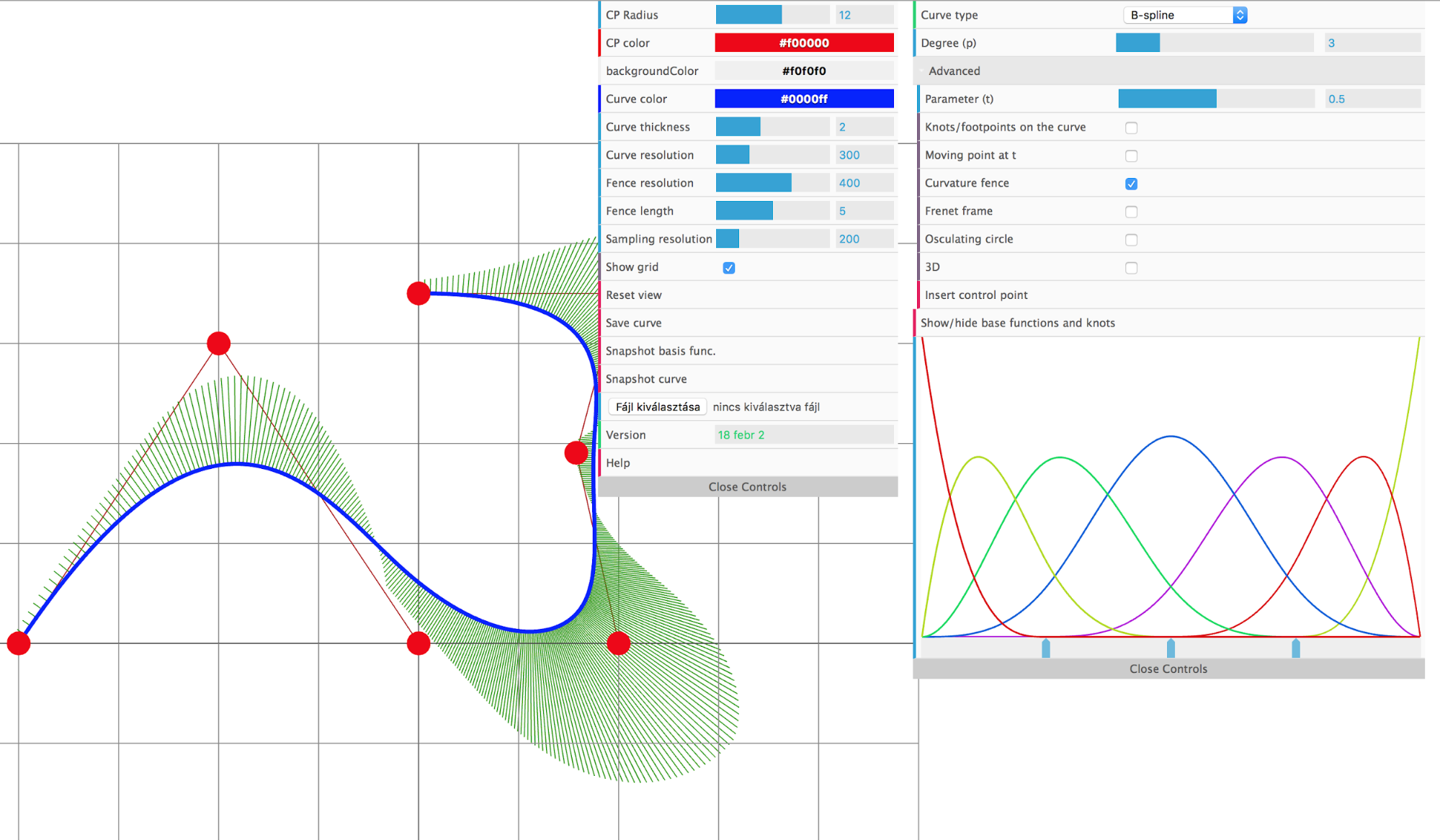
Munkámat az Irányítástechnika és Informatika Tanszék, Számítógépes grafika csoportjában Dr. Várady Tamás vezetésével végeztem. Csoportunkban a számítógépes grafika mellett felületillesztéssel [s7], geometriai kényszerekkel [s6], illetve új görbe és n-oldalú felületreprezentációkkal [s8] is foglalkozunk. Az általunk tartott 3D Számítógépes Geometria és Alakzatrekonstrukció tárgy oktatásához fejlesztettük ki az internetes keretrendszerünket, amelyet az itt bemutatott kutatásunkhoz is használtunk, lásd 2. ábra.

 

 

2. ábra: az általunk fejlesztett internetes keretrendszer felülete.

A kutatás történetének, tágabb kontextusának bemutatása

A parametrikus görbék a geometriai tervezésben nagyon fontos szerepet játszanak. Ezek közül is a legfontosabbak a kontrollpont alapú reprezentációk, ahol a görbét a tervező egy pontsorozattal (vagy az azokat összekötő kontrollpoligonnal) definiálhatja, amelyet a görbe bizonyos értelemben követ. Az egyik legfontosabb ilyen reprezentáció a Bézier-görbe amely Bernstein-polinomokon alapul; ezáltal C∞ folytonosságot lehet biztosítani és a görbék nagyon természetes módon követik a kontrollpoligon alakját, lásd 3. ábra. Ezeket a görbéket először Pierre Bézier alkalmazta a Renaultnál a ‘60-as években, lásd [1].

3. ábra: egy 4-edfokú Bézier görbe. (Interaktív, a kontrollpontok mozgathatóak.)

 

A másik legelterjedtebb reprezentáció a B-spline, amely Bézier szakaszokból épül fel. A B-spline előnye a Bézier-görbékkel szemben, hogy a bázisfüggvények lokálisak, tehát egy adott kontrollpont mozgatása csak a görbe egy jól meghatározott részére hat. Legnagyobb előnye, hogy a fokszám függvényében a görbék kontrollponttól való távolsága állítható, viszont a magasabb deriváltak nem feltétlenül folytonosak, ezért bizonyos iparágakban (például autóipar és optikai tervezés) még mindig a Bézier-görbék a legelterjedtebbek.

A szabványos reprezentációknak számos kiterjesztése jelent meg a szakirodalomban. Ezen kutatások célja, hogy a görbereprezentációkat további paraméterekkel gazdagítsák, és ezáltal  új lehetőségeket biztosítsanak a geometriai tervezésben.

A különböző konstrukciók gyakran használnak trigonometrikus függvényeket, de találhatunk számos exponenciális vagy hiperbolikus függvényeket használó görbét is, lásd [5, 6, 7]. Szintén egy fontos irány a B-spline-ok általánosítása, ahol néhány tulajdonság feladása árán kaphatunk a tervezésben nagyobb szabadságot megengedő görbéket, lásd [2, 3].

A kutatás célja, a megválaszolandó kérdések.

Jól ismert, hogy a Bézier görbék nagyobb számú kontrollpont esetén csak nagyon lazán közelítik a kontrollpoligont, és ezáltal a tervező elvárásait nem vagy csak nehezen követik. A B-spline reprezentáció ezt részben orvosolja, a kontrollpoligonhoz való közelség diszkréten állítható a fokszámmal, azonban alacsony fokszám esetén a görbe simasága is romlik, amely bizonyos alkalmazásoknál elfogadhatatlan.

A kutatás célja egy olyan reprezentáció létrehozása volt, amellyel közvetlenül szabályozható, hogy a görbe milyen mértékben közelítse a kontrollpoligont, és emellett a magasabb fokú deriváltak is folytonosak maradjanak. A dolog nehézsége abban rejlik, hogy a klasszikus reprezentációk számos olyan tulajdonsággal rendelkeznek, amelyek lényegesek a geometriai tervezésben, ezért ezeket egy új reprezentációnak is tudnia kell.

Módszerek

Az eredményeket egy saját fejlesztésű, az interneten is elérhető JavaScript alapú keretrendszerben teszteltük. A keretrendszer segítségével számos görbe tulajdonságot tudunk elemezni.

Az első konstrukciónk az általánosított Mean Value baricentrikus koordinátákon (lásd [4]) alapul. A baricentrikus koordináták egy síkbeli sokszög csúcsaihoz rendelnek folytonos bázisfüggvényeket a síkban. Több ismert konstrukció létezik, az egyik legelterjedtebb a Mean Value koordináták rendszere, amelyek egy sokszögben felvett területek segítségével határozhatók meg.

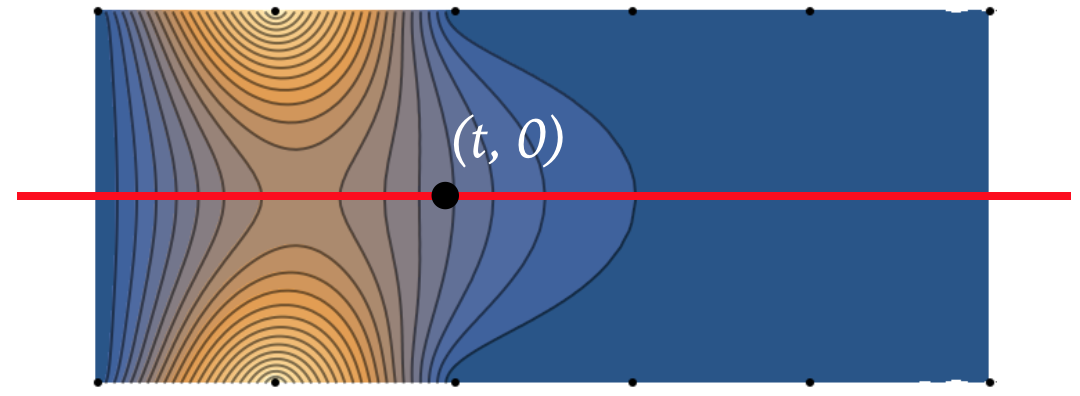
A P-görbéhez tartozó bázisfüggvényeket egy speciális sokszögben (egy téglalap extra pontokkal az oldalain) kiértékelt baricentrikus koordinátákból határozzuk meg, ahol a téglalap magassága adja a proximity paramétert, lásd [s3] és 4. ábra.

 

 

4. ábra: a P-görbéket definiáló Mean value baricentrikus koordináták.

 

A másik görbe konstrukciónkat P-Bézier görbének neveztük, lásd [s2]. Tulajdonságai hasonlóak, mint a fent említett P-görbéknek, de előnyük, hogy a Bézier görbéket közvetlenül  reprodukálni tudjuk, valamint magasabbrendű végponti kényszereket is elő tudunk írni.  A bázisfüggvények algebrai alakja sokkal szebb, és kiszámításuk nem a baricentrikus koordinátákon alapul. A módszer lényege, hogy a Bernstein bázisfüggvényeket felírjuk lineáris spline alakban és a kapott lineáris spline együtthatókat egy speciális négyzetgyökös kifejezés segítségével folytonosan változtatjuk. Ez a módszer teljesen újszerű, hasonló tulajdonságokkal rendelkező görbe nem ismert a szakirodalomban.

A P-Bspline görbéket a B-spline görbék általánosításaként értelmezzük, ahol a görbét a kontrollpontokon kívül egy folytonos proximity paraméter határoz meg, ezáltal a B-spline görbéket is tudja reprodukálni, lásd [s2]. A P-Bézier esetében működő módszert egy az egyben lehet alkalmazni a B-spline-okra; ez mutatja hogy a módszer nagyon általánosan alkalmazható tetszőleges más kontrollpont alapú görbék esetén is.

Interaktív applet. Egy 4-edfokú P-Bézier görbe, proximity érték: 0.50.

Eddigi eredmények

A proximity görbék általános alakja a következő.

Ahol Pi-k a kontrollpontokat jelölik, az Mi-k a bázisfüggvényeket, és ez utóbbiak egy γ proximity (kontrollpoligontól való távolságot szabályozó) paramétertől függenek.

A P-görbék és felületek esetében a Mean Value általánosított baricentrikus koordináták segítségével definiáltunk bázisfüggvényeket, lásd [s3]. Hátrányuk, hogy a klasszikus reprezentációk nem reprodukálhatók, valamint nem adhatók meg magasabb rendű végponti kényszerek sem. Ezen problémákat sikerült kiküszöbölni a P-Bézier és P-Bspline görbék által, lásd [s2].

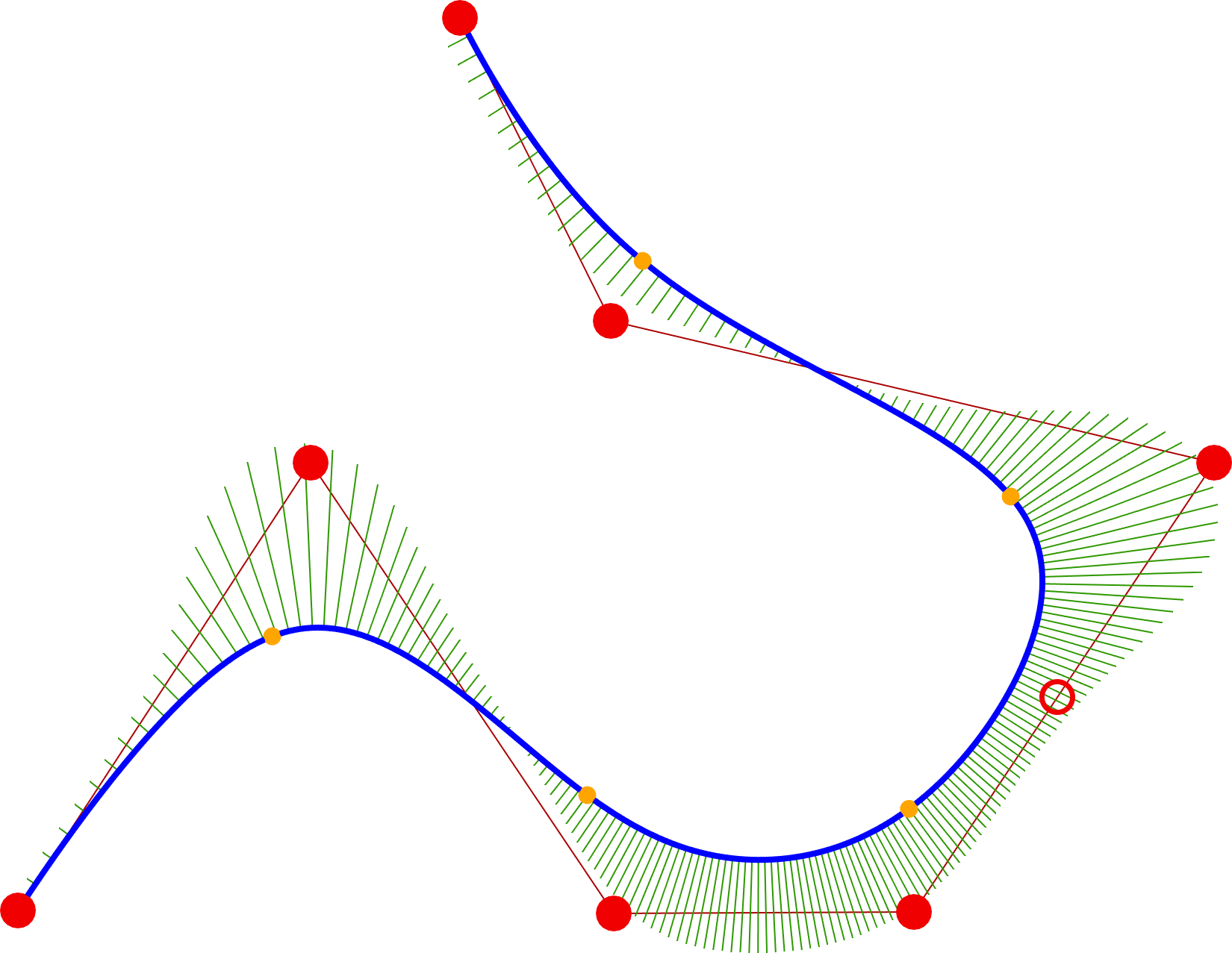
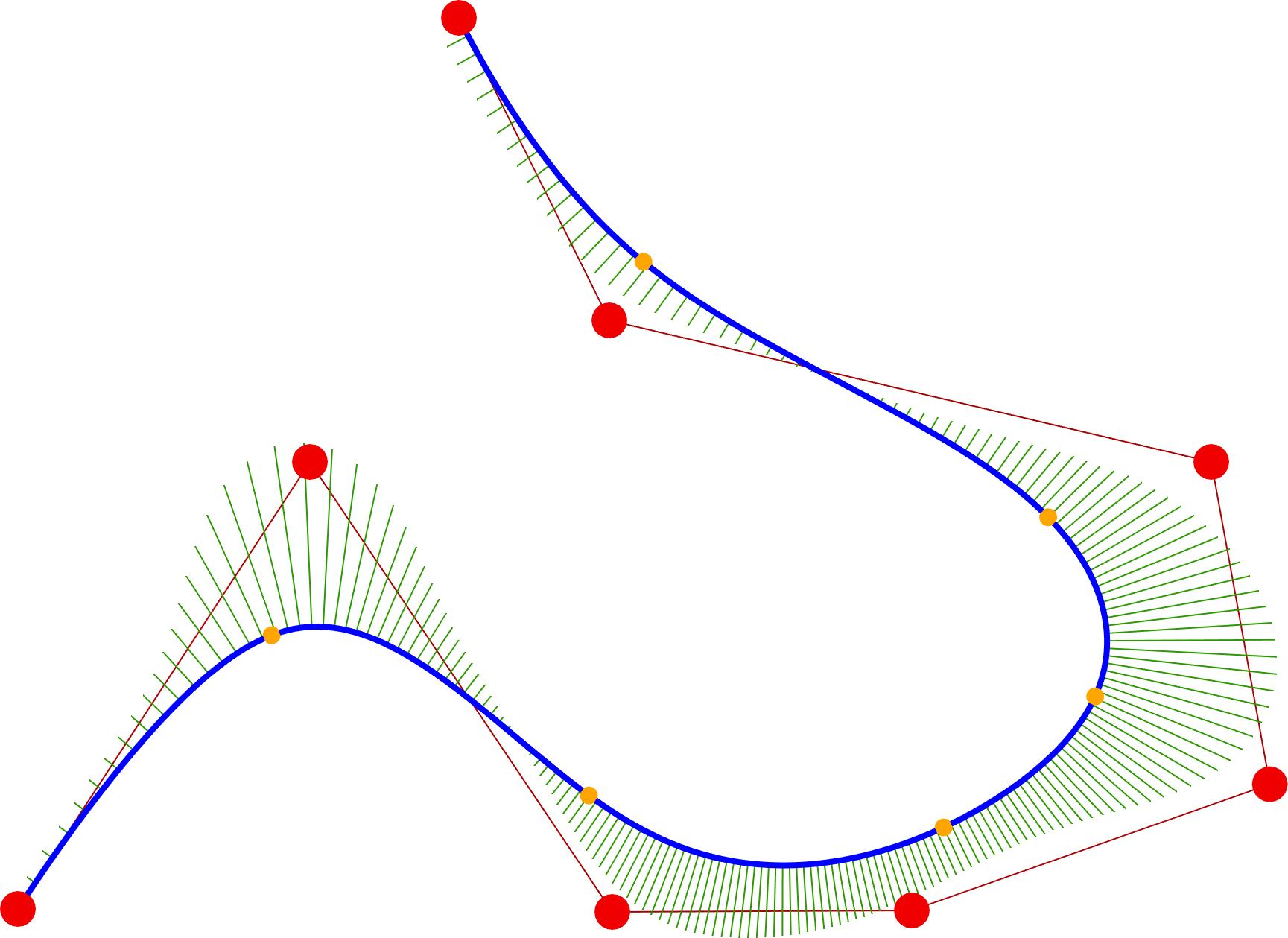
Az új reprezentációk egy további különleges tulajdonsága az egyedi kontrollpont beszúrási algoritmus, amely lehetővé teszi, hogy egy új kontrollpont beszúrásakor se a görbe, se a kontrollpoligon nem változzon meg, lásd 5. ábra.

 

 

5. ábra: kontrollpont beszúrás egy P-Bézier görbén.

 

Az általunk bevezetett proximity görbék legfontosabb tulajdonságai a következők.

• Egy adott kontrollpoligonhoz egy folytonos paramétertől függő görbecsaládot definiálnak.
• A bázisfüggvények pozitívak.
• A bázisfüggvények összege 1.
• Végponti tangens interpoláció (a görbe a kontrollpoligon első és utolsó húrjához hozzásimul).
• C∞ folytonosság (kivéve P-Bspline).
• Harangformájú bázisfüggvények (a függvény egy ideig monoton nő, majd monoton csökken az értelmezési tartományon).
• Magasabbrendű végponti derivált kényszerek megadhatók (csak P-Bézier és P-Bspline).
• Egyedi kontrollpont beszúrási algoritmus (a tervezési szabadsági növelhető új kontrollpontok beszúrásával).

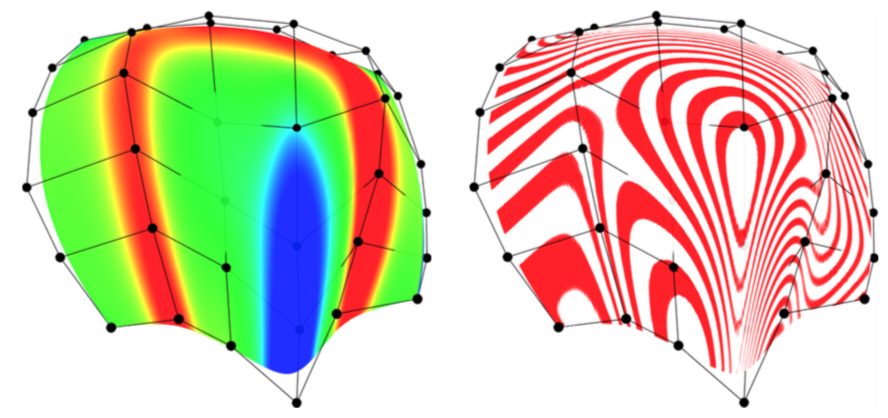
A javasolt reprezentáció természetes módon kiterjeszthető tenzor-szorzat felületekre is, lásd 6. ábra.

 

 

6. ábra: egy tenzorszorzat P-Bézier felület görbülettérképe és fényvonalai.

 

Várható impakt, további kutatás

Az eredményeket két nemzetközi konferencián (Symposium on Solid and Physical Modeling (SPM-2017) Berkeley, USA, 12th International Conference on Geometric Modeling and Processing (GMP 2018) Aachen, Németország [s2, s3]) és három magyar konferencián (IX. Magyar Számítógépes Grafika és Geometria Konferencia (GRAFGEO 2018), Workshop on the Advances of Information Technology (WAIT 2017, 2018) [s1, s4, s5]) mutattam be. A GMP 2018 konferencián Best Paper díjjal jutalmazták a munkánkat.
A szakmai kérdések elsősorban arra vonatkoztak, hogy a görbék mennyire alkalmazhatóak a numerikus analízisben, feloszthatók-e, illetve a szabványos reprezentációkkal mennyire kompatibilisek, így az elkövetkező időszakban elsősorban ezekkel a kérdésekkel szeretnénk foglalkozni. Jelenlegi kutatási témánk még további baricentrikus koordinátákon alapuló görbe és felületreprezentációk létrehozása és az itt említett reprezentációk további kiterjesztése.

 

Saját publikációk, hivatkozások, linkgyűjtemény

Kapcsolódó saját publikációk listája.

 

[s1] István Kovács, Tamás Várady, Kitti Varga. A new set of base functions for parametric curve and surface design. Proceedings of the Workshop on the Advances of Information Technology: WAIT 2017. pp. 101-111. (2017)

 

[s2] István Kovács, Tamás Várady. P-Bézier and P-Bspline curves – new representations with proximity control. Computer Aided Geometric Design, 62: pp. 117-132. (2018)

 

[s3] István Kovács, Tamás Várady. P-curves and surfaces: Parametric design with global fullness control. Computer Aided Design, 90: pp. 113-122. (2017)

 

[s4] István Kovács, Tamás Várady. Approximating point data by P-Bézier curves.  Proceedings of the Workshop on the Advances of Information Technology: WAIT 2018.  (2018)

 

[s5] István Kovács, Tamás Várady. Favorable approximating properties of the P-Bézier basis. IX. Magyar Számítógépes Grafika és Geometria Konferencia, Konferenciakiadvány, pp. 10-15. (2018)

 

További releváns saját publikációk listája.

 

[s6] István Kovács, Tamás Várady, Péter Salvi. Applying geometric constraints for perfecting CAD models in reverse engineering. Graphical Models 82: pp. 44-57. (2015)

 

[s7] István Kovács, Tamás Várady. Case studies for fitting B-spline surfaces with constraints. VIII. Magyar Számítógépes Grafika és Geometria Konferencia, Konferenciakiadvány, pp. 70-78. (2016)

 

[s8] Tamás Várady, Péter Salvi, István Kovács. Enhancement of a multi-sided Bézier surface representation. Computer Aided Geometric Design 55: pp. 69-83. (2017)

 

Linkgyűjtemény.

 

Irányítástechnika és Informatika tanszék és Számítógépes geometria csoport:

https://www.iit.bme.hu, http://cg.iit.bme.hu/portal/

Az általunk fejlesztett online keretrendszer:

http://math.bme.hu/~kovacsi/cagd-applets/Curves.html

3d számítógépes geometria és alakzatrekonstrukció tárgy honlapja: http://cg.iit.bme.hu/portal/node/312

Számítógéppel segített geometriai tervezés: https://en.wikipedia.org/wiki/Computer-aided_design

Parametrikus görbék:

https://en.wikipedia.org/wiki/Parametric_equation

Bézier-görbe:

https://en.wikipedia.org/wiki/Bézier_curve

Pierre Bézier:

https://en.wikipedia.org/wiki/Pierre_Bézier

Bernstein polinomok:

https://en.wikipedia.org/wiki/Bernstein_polynomial

B-spline görbe:

https://en.wikipedia.org/wiki/B-spline

Baricentrikus koordináták:

https://en.wikipedia.org/wiki/Barycentric_coordinate_system

Általánosított baricentrikus koordináták:

http://www.inf.usi.ch/hormann/barycentric/

Symposium on Solid and Physical Modeling (SPM-2017) Berkeley, USA:

https://s3pm.icsi.berkeley.edu/s3pm/spm.html

12th International Conference on Geometric Modeling and Processing (GMP 2018) Aachen, Németország:

http://gmp2018.rwth-aachen.de

IX. Magyar Számítógépes Grafika és Geometria Konferencia (GRAFGEO 2018):

http://cg.iit.bme.hu/portal/grafgeo2018

Workshop on the Advances of Information Technology:

https://www.iit.bme.hu/wait-2018-workshop-advances-information-technology?language=hu

 

Hivatkozások listája.

 

[1] G. E. Farin. Curves and surfaces for CAGD: a practical guide. Morgan Kaufmann, (2002)

 

[2] B. A. Barsky and J. C. Beatty. Local control of bias and tension in beta-splines. ACM Transactions on Graphics (TOG), 2(2):109–134, (1983)

 

[3] T. D. DeRose and B. A. Barsky. Geometric continuity, shape parameters, and geometric constructions for Catmull-Rom splines. ACM Transactions on Graphics (TOG), 7(1):1–41, (1988)

 

[4] M. S. Floater, Generalized barycentric coordinates and applications, Acta Numerica 24 161–214. (2015)

 

[5] X. Han. Cubic trigonometric polynomial curves with a shape parameter. Computer Aided Geometric Design, 21(6):535–548, (2004)

 

[6] W. Wen-Tao and W. Guo-Zhao. Bézier curves with shape parameter. Journal of Zhejiang University-Science A, 6:497–501, (2005)

 

[7] J. Zhang. C-Bézier curves and surfaces. Graphical Models and Image Processing, 61(1):2–15, (1999)