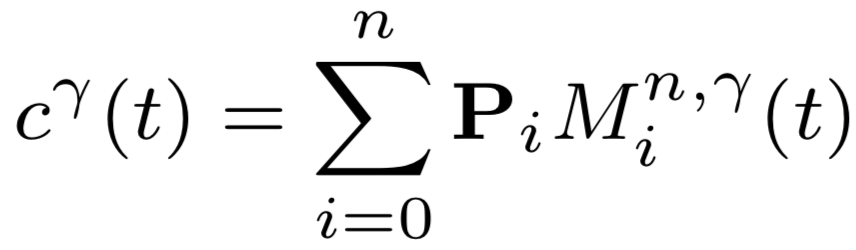Doctoral School of Informatics 

Department of Control Engineering and Information Technology

Supervisor: Dr. Várady Tamás

P-curves and surfaces ─ new representations in computer aided design 

Introducing the research area

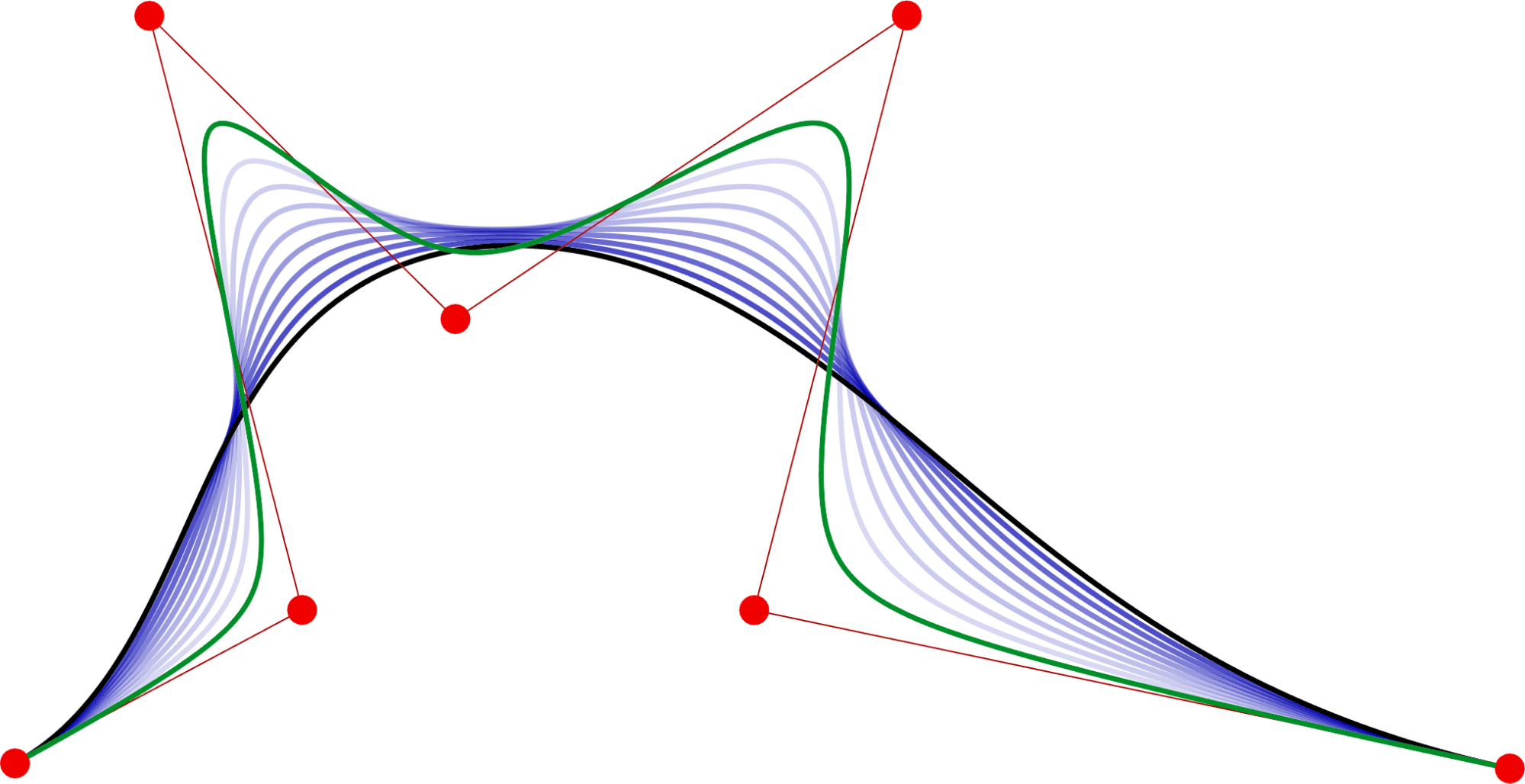
In geometric modelling the great majority of free-form curves and surfaces are defined by control point based representations. The most widely applied Bézier and B-spline schemes possess a well-established theory with a long list of attractive features, see [1]. It is a recurring research topic to develop new schemes where certain improvements are possible. Proximity curves represent a family of curves that are associated with a given parametric curve, depending on a proximity value, that determines the location of an intermediate curve and its fullness (or tension). Meanwhile, it preserves various advantageous properties of the classical representations. See Figure 1 and our online framework.

 

 

Figure 1: P-Bézier curves with several values of proximity parameter.

 

Brief introduction of the research place

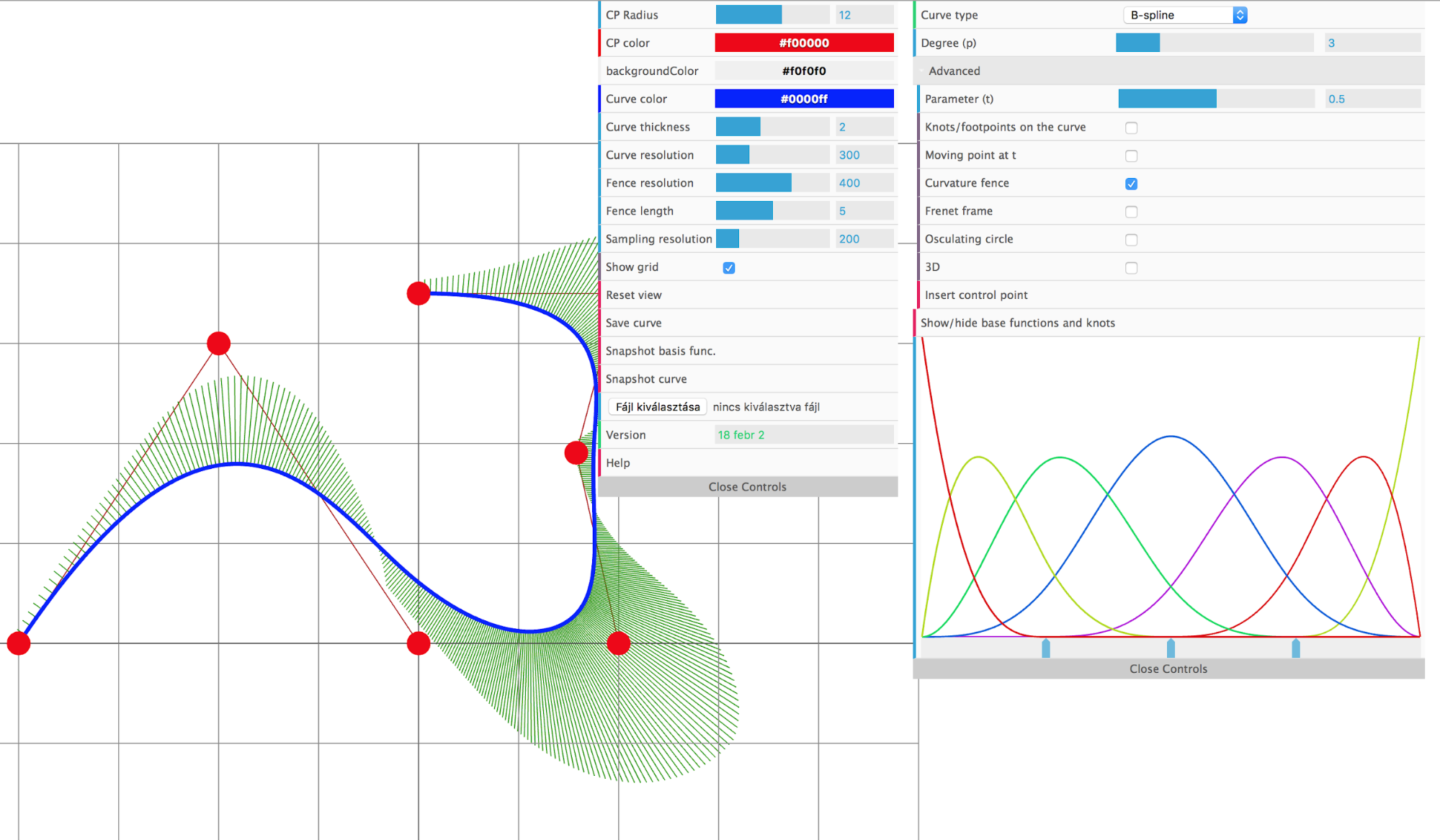
My advisor is Dr. Tamás Várady, Department of Control Engineering and Information Technology, Computer Graphics group. The group works not only on computer graphics, but also on surface fitting [s7], geometric constraints [s6], new curve and n-sided surface representations [s8]. Our online framework was developed for teaching the course 3D computer geometry and shape reconstruction, and it is also used for this research, see Figure 2.

 

 

Figure 2: our online JavaScript-based framework.

 

History and context of the research

Parametric curves play an important role in geometric design. The most widely used ones are the control point based representations, where the curves are defined by control points (or a control polygon). One of these representations is called Bézier curve that is based on Bernstein polynomials. Therefore, it maintains C∞ continuity and the curve approximates the control polygon naturally. These curves were first applied by Pierre Bézier at Renault in the 1960s for designing automobiles, see [1].

Figure 3: a Bézier curve of degree 4.

 

Another well-known representation is called B-spline, which is built from Bézier segments. One of their advantages over the Bézier curves is that their control points have only local effect on them. The degree of the curve can control the distance between the curve and the control polygon. However, the higher degree derivatives are not necessarily continuous, therefore Bézier curves are more widely used in some specific areas (like automotive industry and optical design).

Various extensions of the standard representations has been published. The aim of these methods is to enrich the original curve representations with more parameters, ensuring new possibilities in design. Several methods often use trigonometric functions, but there are curves with exponential or hyperbolic base functions as well, see [5, 6, 7]. Extending B-spline representations is a well-studied area, too.  See [2, 3].

The research goals, open questions

It is well-known for Bézier curves that as the number of control points grows higher, the effect of the basis functions decreases. Then accordingly, the curves approximate the control polygons loosely, and even a large displacement of a control point can change the shape to a small extent only. For B-spline curves proximity is related to the degree of the curve d, and it changes in discrete steps but it can maintain only Cd continuity.

The goal of our research is to introduce a family of proximity curves that retains C∞ continuity and pseudo-local control, and is capable to produce a sequence of continuously changing shapes, approximating a given control polygon. Moreover, it should retain many features of the classical representations that are important in geometric design.

Methods

Our results are tested in a JavaScript-based framework developed by us, where many features of the curves can be analysed.

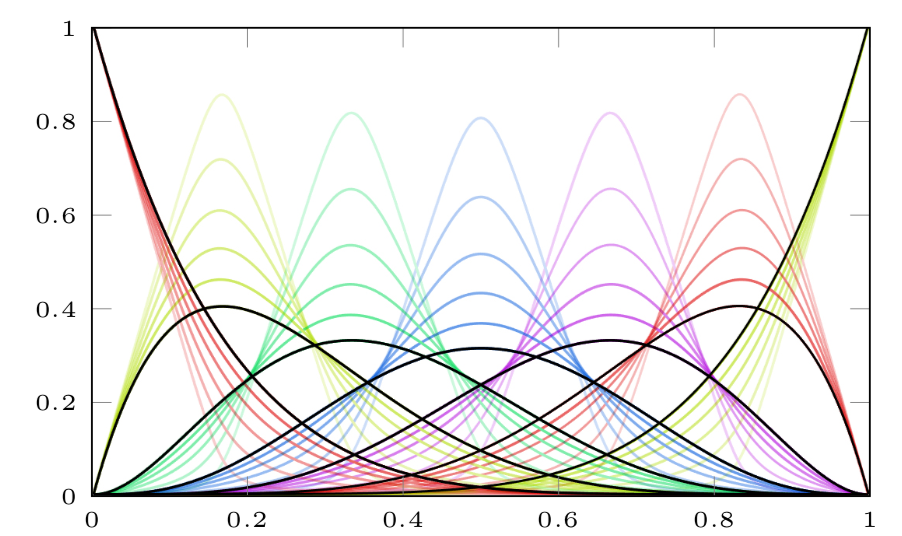
In our first approach (P-curves) the basis functions were constructed by means of generalized barycentric coordinates. The generalized barycentric coordinates are smooth functions assigned to vertices of a polygon on the plane. One of these constructions is the Mean Value coordinates that can be calculated with the help of specific areas in the polygon, see [4].

The basis functions of the P-curves are calculated from the barycentric coordinates of a special polygon (a rectangle with extra vertices on its sides). The height of the rectangle is the proximity parameter, see [s3] and Figure 4.

 

 

Figure 4: the Mean Value barycentric coordinates that define the P-curves.

 

Our other curve representation is called P-Bézier curve, see [s2]. Its properties are similar to the previously mentioned P-curve, but it directly reproduces the Bézier curves, and higher degree of endpoint constraints can be enforced. The algebraic form of the basis functions is simpler, since they are not calculated from barycentric coordinates. They can be constructed by expressing the Bernstein basis functions in the linear spline form and modifying the obtained coefficients with a continuous transition. This method is a completely new approach, no other curve representation with similar properties is known in this research area.

The P-Bspline curves are generalizations of the B-spline curves. These curves are defined not only by the control points but also by a proximity parameter and B-spline curves are reproducible as well, see [s2]. The method of the P-Bézier curve can be directly applied for B-splines, and also for any other control point based curves.

 

Interactive application. A degree 4 P-Bézier curve with proximity of 0.50.

Results

The general form of the proximity curves is the following.

Where Pi’s denote the control points and Mi’s the basis functions that are defined by the γ proximity parameter.

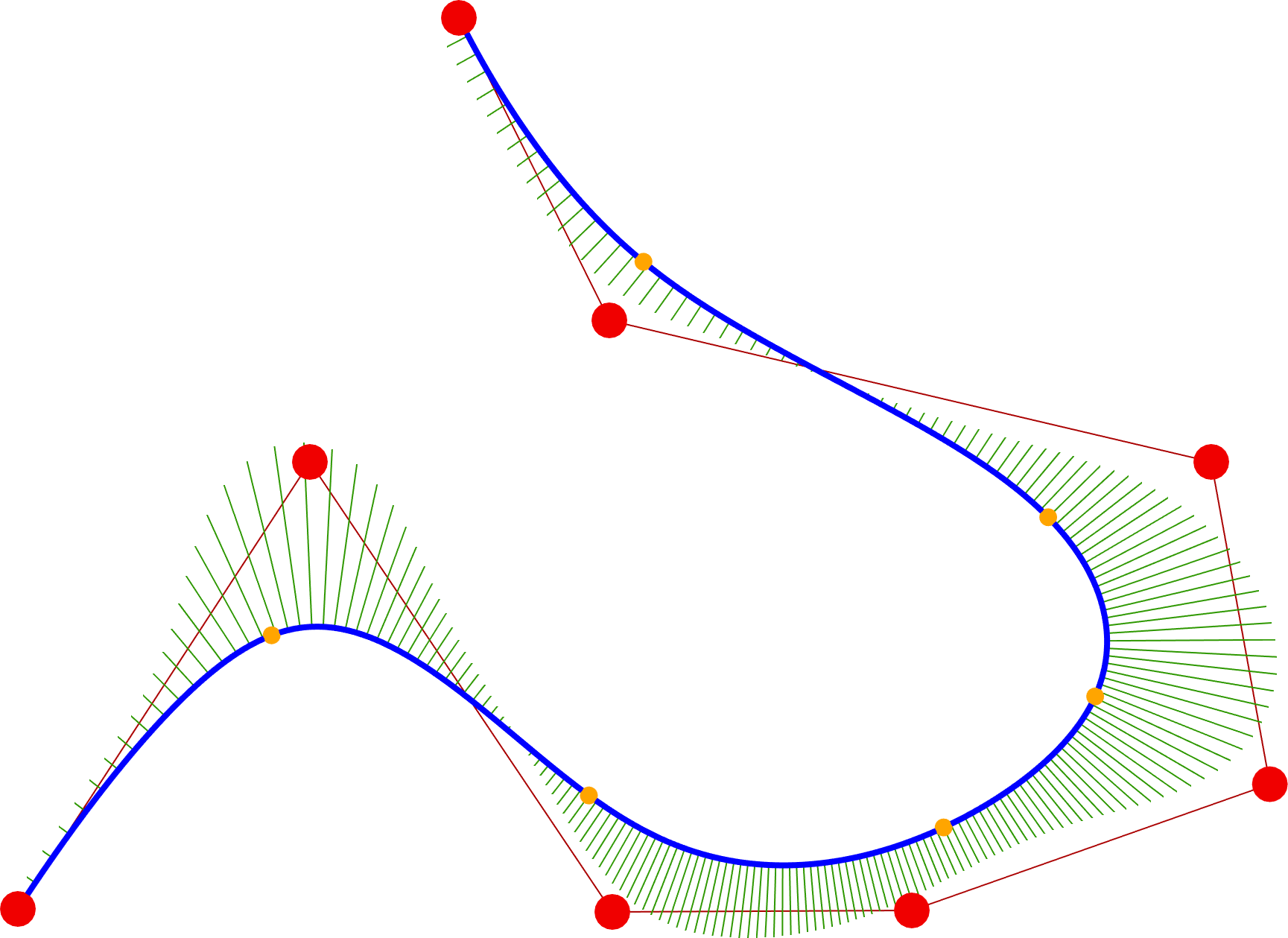
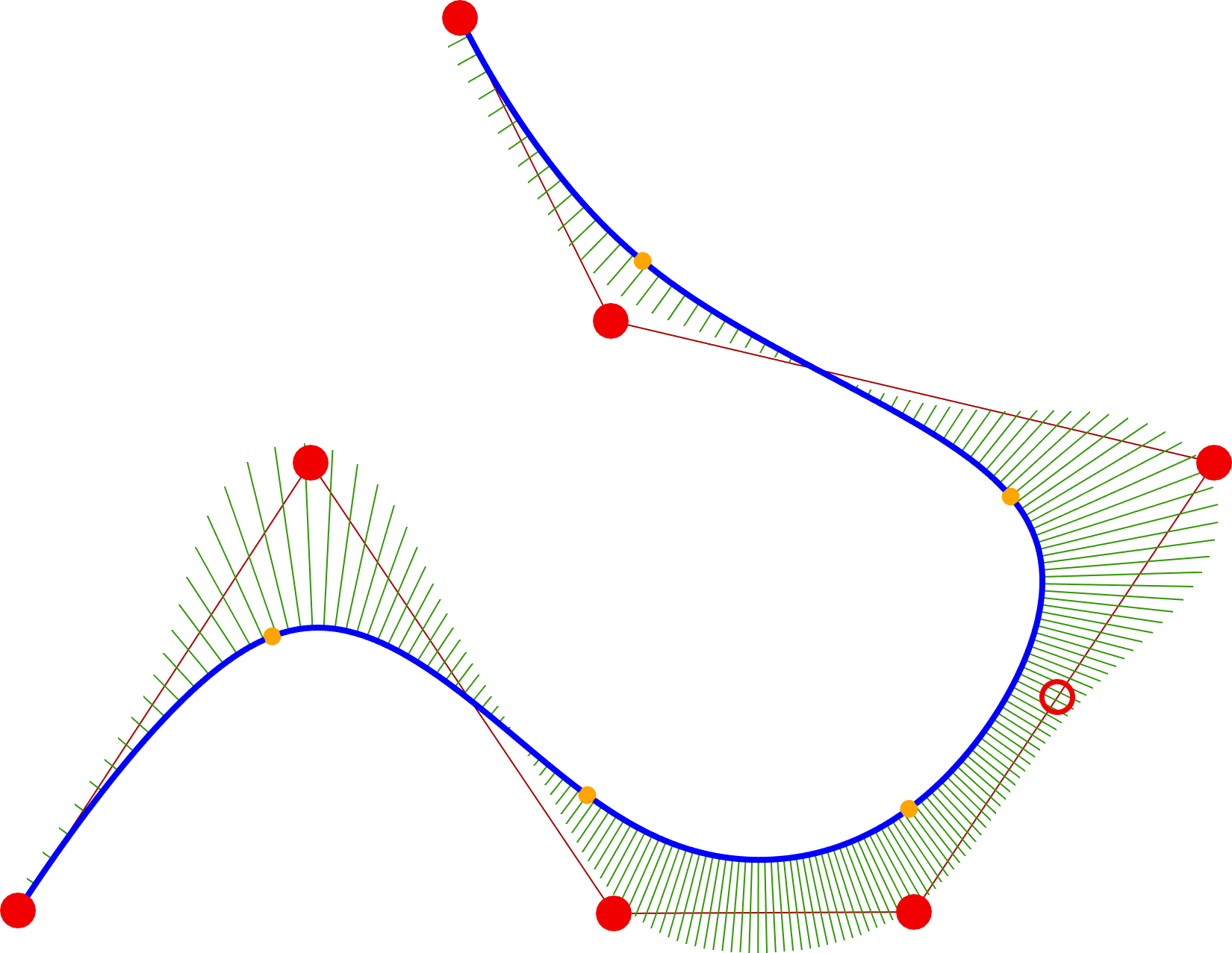
The P-curves and surfaces are based on generalized barycentric coordinates. Their drawbacks are that the classical curves are not reproducible and higher endpoint constraints cannot be prescribed, see [s3]. P-Bézier and P-Bspline curves overcome these obstacles. Another feature of these new representations is the special control point insertion procedure that enables the curve and the control polygon to maintain their original forms, see [s2] and Figure 5.

 

 

 

Figure 5: control point insertion on a P-Bézier curve.

 

 

The most important properties of our proximity curves are the following.

• They form a family of curves that belongs to a given control polygon and is defined by a continuous parameter.
• The basis functions are positive.
• The sum of the basis functions is 1.
• Endpoint tangent interpolation (the curve and the first and last cord of the control polygon meet smoothly).
• C∞ continuity (except for P-Bspline).
• Bell-shaped basis functions (the functions are monotone increasing then monotone decreasing in the domain).
• Higher endpoint derivative constraints can be prescribed (only for P-Bézier and P-Bspline).
• Special control point insertion procedure (for higher degree of freedom in design).

 

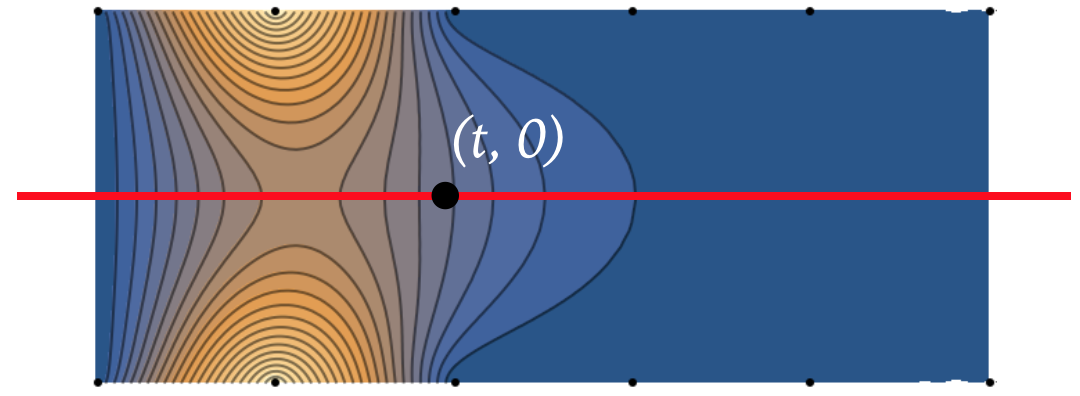
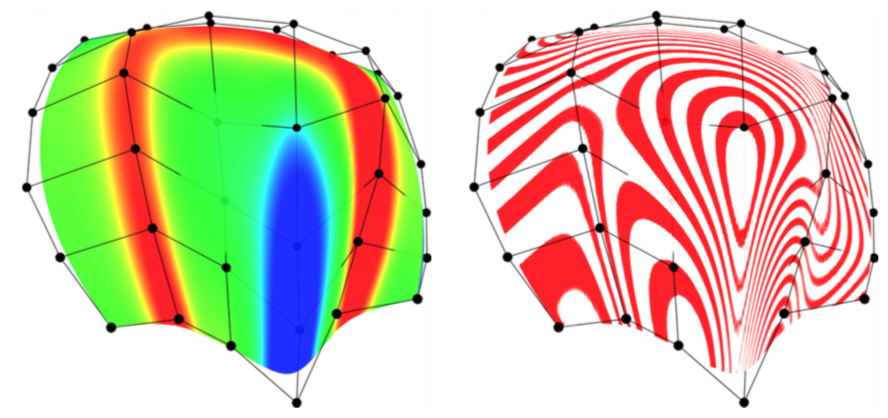
These representations can be naturally generalized for tensor-product surfaces, see Figure 6.

 

 

Figure 6: the curvature map and the isophotes of a tensor-product P-Bézier surface.

 

Expected impact and further research

 

Our results were presented in two international conferences (Symposium on Solid and Physical Modeling (SPM-2017) Berkeley, USA, 12th International Conference on Geometric Modeling and Processing (GMP 2018) Aachen, Germany, [s2, s3]) and three hungarian conferences (IX. Magyar Számítógépes Grafika és Geometria Konferencia (GRAFGEO 2018), Workshop on the Advances of Information Technology (WAIT 2017, 2018),  [s1, s4, s5]). In the GMP 2018 conference we received a Best Paper award.

Our future work contains further analysis of the curves: usability in numerical analysis, subdivision, compatibility with standard representation schemes. We also plan to create other curve and surface representations based on barycentric coordinates and to extend the above mentioned representations.

 

Publications, references, links

List of corresponding own publications.

 

[s1] István Kovács, Tamás Várady, Kitti Varga. A new set of base functions for parametric curve and surface design. Proceedings of the Workshop on the Advances of Information Technology: WAIT 2017. pp. 101-111. (2017)

 

[s2] István Kovács, Tamás Várady. P-Bézier and P-Bspline curves – new representations with proximity control. Computer Aided Geometric Design, 62: pp. 117-132. (2018)

 

[s3] István Kovács, Tamás Várady. P-curves and surfaces: Parametric design with global fullness control. Computer Aided Design, 90: pp. 113-122. (2017)

 

[s4] István Kovács, Tamás Várady. Approximating point data by P-Bézier curves.  Proceedings of the Workshop on the Advances of Information Technology: WAIT 2018.  (2018)

 

[s5] István Kovács, Tamás Várady. Favorable approximating properties of the P-Bézier basis. IX. Magyar Számítógépes Grafika és Geometria Konferencia, Konferenciakiadvány, pp. 10-15. (2018)

 

List of relevant own publications.

 

[s6] István Kovács, Tamás Várady, Péter Salvi. Applying geometric constraints for perfecting CAD models in reverse engineering. Graphical Models 82: pp. 44-57. (2015)

 

[s7] István Kovács, Tamás Várady. Case studies for fitting B-spline surfaces with constraints. VIII. Magyar Számítógépes Grafika és Geometria Konferencia, Konferenciakiadvány, pp. 70-78. (2016)

 

[s8] Tamás Várady, Péter Salvi, István Kovács. Enhancement of a multi-sided Bézier surface representation. Computer Aided Geometric Design 55: pp. 69-83. (2017)

 

Table of links.

 

Department of Control Engineering and Information Technology and Computer Graphics group:

https://www.iit.bme.hu, http://cg.iit.bme.hu/portal/

Our online framework:

http://math.bme.hu/~kovacsi/cagd-applets/Curves.html

3D computer geometry and shape reconstruction course web page:

http://cg.iit.bme.hu/portal/node/312

Computer aided design:

https://en.wikipedia.org/wiki/Computer-aided_design

Parametric curves:

https://en.wikipedia.org/wiki/Parametric_equation

Bézier curve:

https://en.wikipedia.org/wiki/Bézier_curve

Pierre Bézier:

https://en.wikipedia.org/wiki/Pierre_Bézier

Bernstein polynomials:

https://en.wikipedia.org/wiki/Bernstein_polynomial

B-spline curve:

https://en.wikipedia.org/wiki/B-spline

Barycentric coordinates:

https://en.wikipedia.org/wiki/Barycentric_coordinate_system

Generalized barycentric coordinates:

http://www.inf.usi.ch/hormann/barycentric/

Symposium on Solid and Physical Modeling (SPM-2017) Berkeley, USA:

https://s3pm.icsi.berkeley.edu/s3pm/spm.html

12th International Conference on Geometric Modeling and Processing (GMP 2018) Aachen, Germany:

http://gmp2018.rwth-aachen.de

IX. Magyar Számítógépes Grafika és Geometria Konferencia (GRAFGEO 2018):

http://cg.iit.bme.hu/portal/grafgeo2018

Workshop on the Advances of Information Technology:

https://www.iit.bme.hu/wait-2018-workshop-advances-information-technology?language=hu

 

 

List of references.

 

[1] G. E. Farin. Curves and surfaces for CAGD: a practical guide. Morgan Kaufmann, (2002)

 

[2] B. A. Barsky and J. C. Beatty. Local control of bias and tension in beta-splines. ACM Transactions on Graphics (TOG), 2(2):109–134, (1983)

 

[3] T. D. DeRose and B. A. Barsky. Geometric continuity, shape parameters, and geometric constructions for Catmull-Rom splines. ACM Transactions on Graphics (TOG), 7(1):1–41, (1988)

 

[4] M. S. Floater, Generalized barycentric coordinates and applications, Acta Numerica 24 161–214. (2015)

 

[5] X. Han. Cubic trigonometric polynomial curves with a shape parameter. Computer Aided Geometric Design, 21(6):535–548, (2004)

 

[6] W. Wen-Tao and W. Guo-Zhao. Bézier curves with shape parameter. Journal of Zhejiang University-Science A, 6:497–501, (2005)

 

[7] J. Zhang. C-Bézier curves and surfaces. Graphical Models and Image Processing, 61(1):2–15, (1999)