Doctoral School of Physics 

Department of Atomic Physics

Supervisor: Dr. Erdei Gábor

Theoretical and experimental investigation, and numerical modeling of human visual acuity

Introducing the research area

Cataract, which manifests as increased light scattering in the patient’s eye, causes vision loss and may lead to blindness in extreme cases. It is cured by implanting artificial intraocular lenses (IOLs), which is one of the most frequently performed surgical procedures. Clinically applied artificial lenses, however, cannot restore all features of the subject’s own crystalline lens. Their main drawback is their incapability to accommodate, and that they cannot eliminate chromatic aberrations, which generates an increasing need to improve image quality [1]. Accordingly, manufacturers continuously develop their IOL products, and allocate more resources for the precise design, personalization, and optimization of lenses. It is important therefore, to relate the well-measurable (objective) physical parameters used in optical design to the subjective visual acuity value used by ophthalmologists to describe the perceived resolving power of the eye [2, 3].

 

Brief introduction of the research place

My research has been carried out at the Department of Atomic Physics, BME, in collaboration with ophthalmologists at the Department of Ophthalmology, Semmelweis University, related to the project entitled "Medical technological research and development on the efficient cure of cataract", led by Medicontur Medical Engineering Ltd.. The main purpose of the project is to develop intraocular lenses that provide more comfortable visual experience than current clinically available products.

 

History and context of the research

When IOLs were first introduced, cataract typically was a disease of the elderly, and patients were satisfied with the image quality achieved by simple lenses applying only spherical surfaces and having fix focal length. In contrast, nowadays cataract is spreading even among subjects in the active age bracket. Accordingly, it has become necessary to provide better correction for visual defects, and to resolve focusing without additional glasses. Furthermore, physiological aspects have emerged based on surgical experience: ophthalmologists cut small wounds to facilitate recovery and to reduce post-operative complications [1].
However, to achieve a significant improvement, the optical development and optimization of IOL parameters have to be complemented by neural aspects too, because the neural transfer and additive noise also influence the cortical image recognized by the subject [2, 3, 4, 8]. In addition, the efficacy of medical treatment is determined by the measurable progression between the pre- and postoperative visual acuity values, that requires more accurate procedures than standard clinical trials. Thus, research and development have to be extended to vision modeling and evaluation methods, too [5, 6].

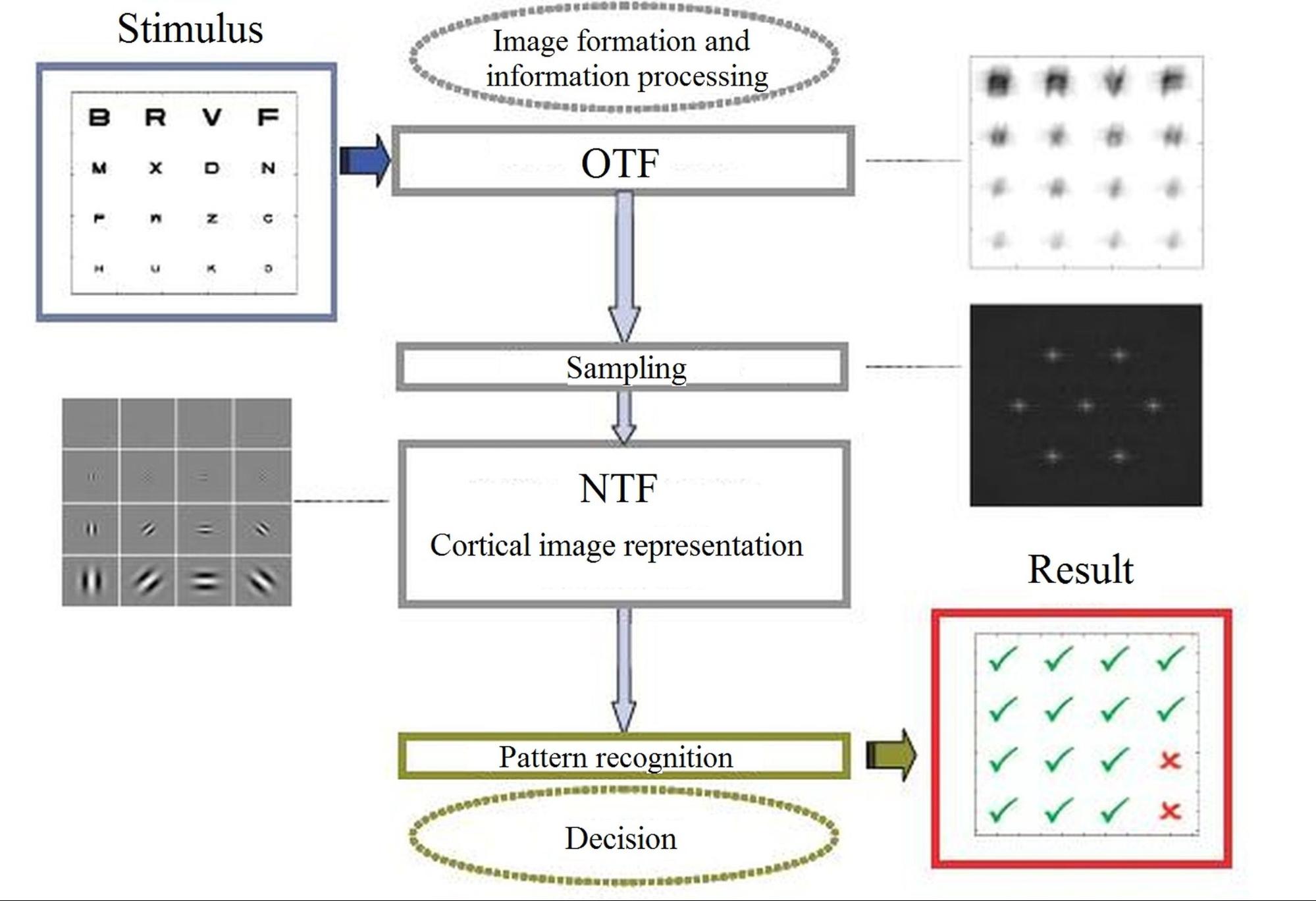
Fig. 1. Main steps of the human visual train: optical imaging, neural transfer and additive noise, and cortical character recognition [8].

 

The research goals, open questions

The research has been carried out as part of a Hungarian consortial cooperation with the primary purpose of improving best achievable vision quality by implanting intraocular lenses. This requires a detailed analysis of all parameters affecting human visual acuity. Therefore, my goal is to develop a neurophysiological vision model that takes the features of neural transfer and cortical pattern recognition into account beyond the optical imaging parameters of the eye. Such a model would enable optimizing directly for visual acuity in optical design (e.g. IOL design), instead of maximizing the optical parameters. In order to calibrate the model, the simulated visual acuity has to be compared to real acuity test results. However, due to the relatively high repeatability error of standard clinical measurements [5, 7], these trials are not sufficient for the calibration. Thus, a new measurement and evaluation method is required, which determines visual acuity with minimal uncertainty and without systematic errors. My purpose is to develop a measurement protocol aligned with the clinical standard that can be used both in research and everyday clinical practice. The new method allows performing high precision acuity tests, which increases the reliability and comparability of measurements.

 

Methods

The primary goal of my vision model is to determine the relation between well-measurable physical parameters describing the optical properties of human eye, and the visual acuity value used by ophthalmologists to characterize perceived vision quality. Acuity models presented in literature usually apply wavefront aberration expressed in optical path difference (OPD) as input parameter, because it characterizes all monochromatic aberrations of the eye simultaneously, and it can be routinely measured by Shack-Hartmann sensors (see Fig. 2) [2, 3, 9]. These models realize a straightforward monochromatic optical transfer, which is not accurate enough for the purpose of IOL design. Thus, I choose to base my model on a physiologically accurate eye model implemented in an optical design software, which allows taking chromatic aberrations into account.

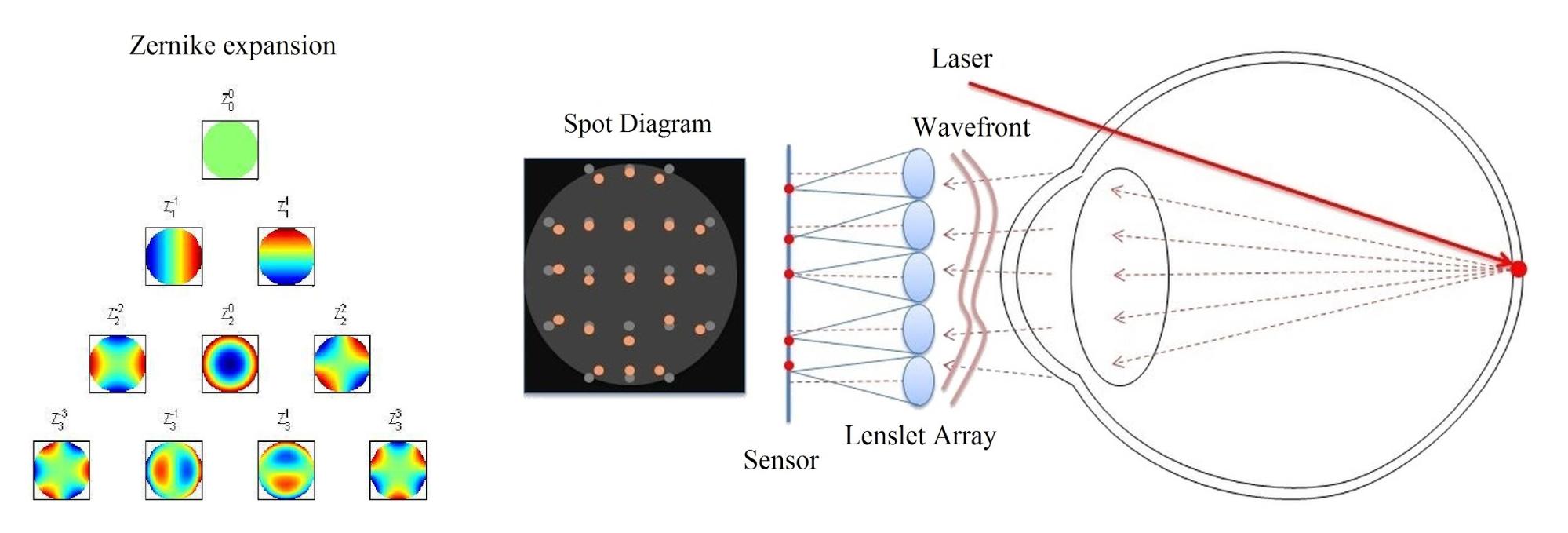
Fig. 2. Wavefront aberration measurement by a Shack-Hartmann sensor [9].

 

In order to accurately model and simulate visual acuity, an efficient image processing algorithm has to be realized, besides the appropriate selection and precise measurement of the input parameters. Since biological visual systems are considered linear, I have implemented the filtering processes of optical imaging and neural transfer in Fourier domain, where spatial domain convolution calculation simplifies to multiplication. Furthermore, to enhance the efficiency of the evaluation, I introduced a new scoring method that significantly reduces random error [S1, S2].

In conventional visual acuity tests, the subject's task is to correctly recognize letters of decreasing size placed in an eye chart. In clinical practice, the examiner registers only the fact whether or not the optotypes are identified correctly, and determines the visual acuity value based on recognition probability. However, in some cases, the examiner omits minor errors (e.g. misidentifying C as O, or F as P), that suggests that human visual perception is more complex than a simple binary scheme (correct/incorrect). Accordingly, I have developed a new scoring method that provides more information about vision quality than the simple binary approach. I defined the correlation of the letters of the English alphabet, which allows assessing how bad or good the answer is, and thus quantifies the degree of misrepresentation, not just the mere fact of it. The correlation of the letters has been quantified by Pearson’s cross-correlation, so that the result is directly comparable to conventional binary scoring [S1, S2]. Fig. 3 illustrates the correlation-based scoring scheme for the uppercase letters of the English Alphabet.

Fig. 3. Illustration of the new correlation-based scoring method. Rows/columns have been sorted according to their average OC. Similar letter pairs are positioned toward the bottom-right corner, while dissimilar pairs are to the top-left corner.

 

Results

During my PhD research, I have implemented a neurophysiological vision model that comprises a physiologically accurate schematic eye, and considers the neural transfer, additive noise and cortical character recognition, too. [S4]. The input parameters of the model are the subject’s wavefront aberration and pupil diameter, based on which the individual polychromatic Point Spread Function (PSF), defining the optically filtered retinal image, is determined in the eye model (see Fig. 4).

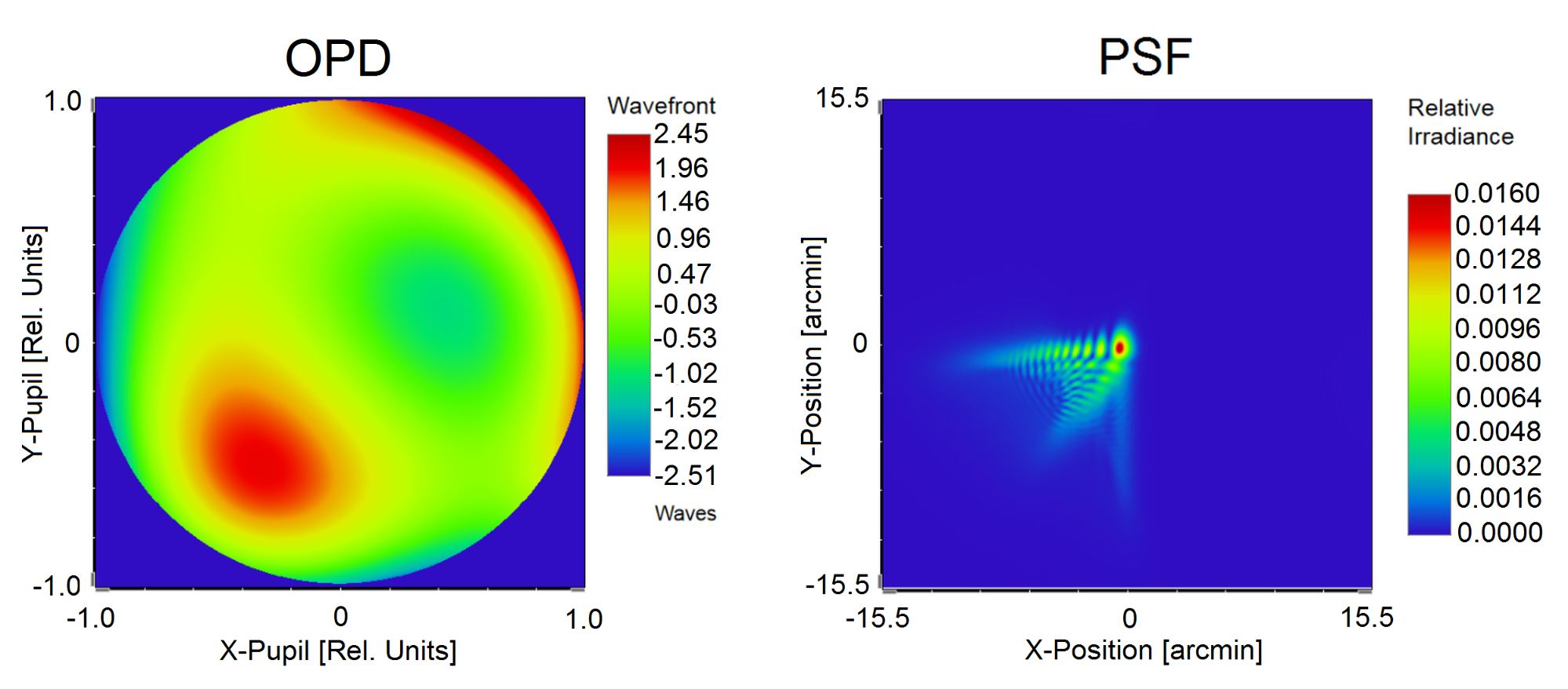
Fig. 4. Determination of the polychromatic PSF by my physiological eye model personalized based on the measurement of wavefront aberration characterized by optical path difference (OPD).

 

As cortical character recognition is significantly influenced by the preliminary knowledge of the template set, tested subjects need to be literate. Therefore, conventional acuity measurement cannot be performed on preschool children and on illiterate adults in its current form. In contrast, my vision model is based on objective input parameters, which allows performing personalized acuity simulations for all subjects. As the measurement of neural performance is not as precise and widely accepted as using Shack-Hartmann sensor for measuring optical aberrations, the neural transfer is considered to be fix in our model for each subject. It is determined based on data presented in the literature describing healthy subjects with average normal vision [3, 4]. The next step is to model neural noise, which characterizes the changes and uncertainties of the nervous system over time and between individuals. The results of the successive steps of opto-neural image processing are illustrated in Fig. 5. The output of the entire procedure is the noisy cortical representation of the image, which the patient attempts to recognize.

Fig. 5. The results of the successive steps of image processing performed by my vision model: a) ideal image of the letter under examination, b) retinal image, c) (post-retinal) neural representation, d) noisy image.

 

Additionally to individual visual acuity simulations, the model enables to classify and rank the effects of environmental circumstances that affect vision quality. It also allows quantifying measurement errors caused by these factors by analyzing the simulations. Our result showed that the illumination of the examination room and the pupil size significantly influence visual acuity, which is in good agreement with the statements presented in the literature [5, 6]. Furthermore, the repeatability of the measurements has been assessed, which concludes that standardization is required.

In order to calibrate my model, I performed high precision visual acuity tests with my measurement setup developed specifically for this purpose. Since the pupil size significantly affects visual acuity, I supplemented the system with real time monitoring of the pupil diameter during the acuity test [S3]. The measurement layout is illustrated in Fig. 6.

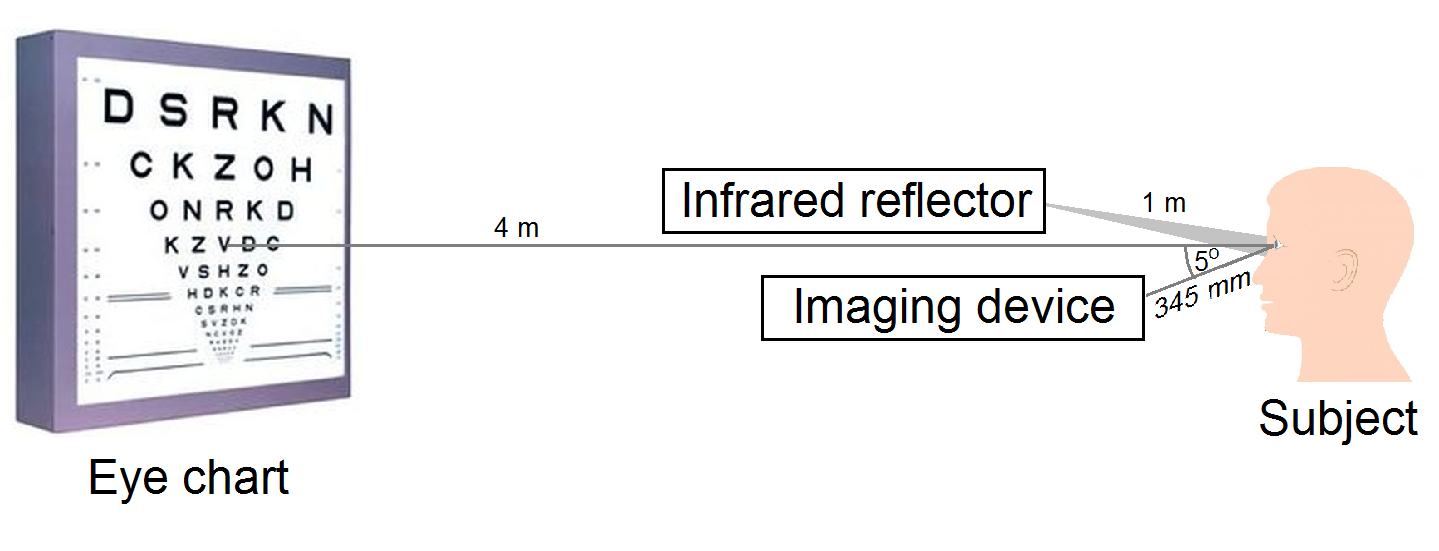
Fig. 6. Measurement setup for monitoring pupil size during visual acuity tests.

To evaluate the captured pupil images, I developed a Hough transform-based algorithm that uses the size of the corneal limbus (iris outer rim) as reference to eliminate magnification error caused by the subject’s motion (see Fig. 7). According to my experimental results, the sensitivity of the pupil diameter measurement exceeds the accuracy of commercially available far-field systems and provides accurate data for visual acuity simulations [S3].

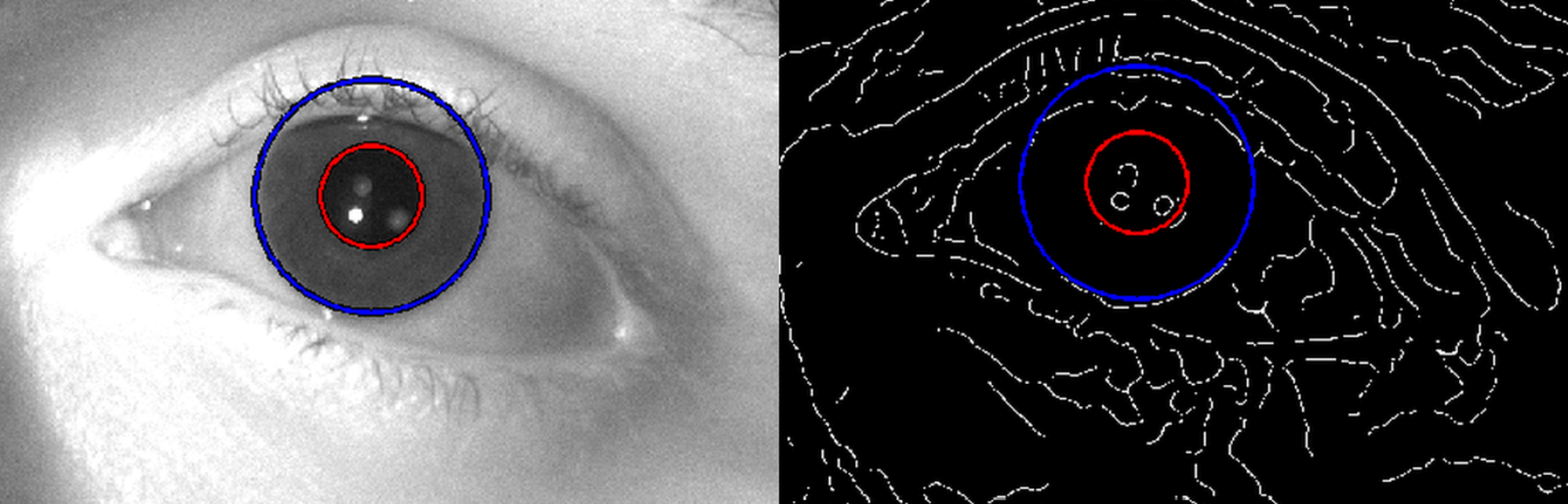
Fig. 7. Determination of the pupil diameter by my Hough transform-based algorithm that takes the corneal limbus (i.e. iris outer rim) size as reference to eliminate magnification error caused by the subject’s motion.

 

The comparison of simulation and measurement results showed good agreement, which supports the applicability of the vision model. Furthermore, according to the experiments performed on the calibration group, the residual of the simulations is significantly lower than the repeatability of standard visual acuity tests [S4]. In order to extend the clinical applicability of the measurement method, I have developed a protocol aligned with the ophthalmological standard, which makes it possible to perform acuity tests in everyday clinical practice, with significantly better repeatability than conventional trials [S5]. Based on the experiments carried out among various circumstances and simulations performed with different parameters, the new correlation-based scoring method decreases uncertainty error by 20-30% depending on the test parameters [S2, S5].

 

Expected impact and further research

The correlation-based scoring system enables to perform high precision visual acuity measurements for research purposes, and to carry out vision tests aligned with the ophthalmological standard, but with significantly lower random error than the conventional procedure. In addition, my neurophysiological vision model allows accomplishing acuity simulations, and to optimize directly for visual acuity in optical design, either with personalized or an average eye model. Since the method is based on objective measurements, after a clinical calibration performed on an extended subject group, it may provide an alternative approach to determine the quality of vision even for preschool children and illiterate adults. Furthermore, due to the reduced error, the simulation algorithm may be applied to accurately predict postoperative visual acuity after cataract surgery, which significantly contributes to individual IOL design.

 

Publications, references, links

List of corresponding own publications.

S1. Erdei, G., Fülep, Cs. (2018). Measuring visual acuity of a client. World Intellectual Property Organization, WO/2018/020281 A1, PCT/HU2016/000050.

S2. Fülep, Cs., Kovács, I., Kránitz, K., Erdei, G. (2017). Correlation-based evaluation of visual performance to reduce the statistical error of visual acuity. Journal of the Optical Society of America A, 34(7), 1255-1264.

S3. Fülep, Cs., Erdei, G. (2017). Far-field infrared system for the high-accuracy in-situ measurement of ocular pupil diameter. IEEE Proceedings of the 10th International Symposium on Image and Signal Processing and Analysis, 31-36.

S4. Fülep Cs., Kovács I., Kránitz K., Erdei G. (2018). Simulation of visual acuity by personalizable neuro-physiological model of the human eye, Scientific Reports, under submission. 

S5. Fülep Cs., Kovács I., Kránitz K., Nagy Z. Zs., Erdei G. (2018). Application of correlation-based scoring scheme for visual acuity measurements in the clinical practice. Translational Vision Science & Technology, under submission.

 

Table of links.

Medicontur Medical Engineering Ltd.

Department of Atomic Physics, BME

Department of Ophthalmology, Semmelweis University

Cataract

Visual acuity

Point Spread Function

Hough transform

 

List of references.

1. Jinabhai, A. N., Young, G., Hall, L. A., Wolffsohn, J. S. (2013). Clinical techniques to assess the visual and optical performance of intraocular lenses: a review. In D. Navarro (Ed.), Cataracts and cataract surgery: types, risk factors, and treatment options. Eye and vision research development, Nova science.
2. Nestares, O., Navarro, R., Antona, B. (2003). Bayesian model of Snellen visual acuity. Journal of the Optical Society of America A, 20, 1371-1381.
3. Watson, A. B., Ahumada, A. J. Jr. (2008). Predicting visual acuity from wavefront aberrations. Journal of Vision, 8(4):17, 1–19.
4. Watson, A. B., Ahumada, A. J. Jr. (2015). Letter identification and the Neural Image Classifier. Journal of Vision, 15(2):15, 1–26.
5. Rabbetts, R. B. (2007). Bennett and Rabbetts’ Clinical Visual Optics. Butterworth-Heinemann, Elsevier.
6. Duane, T. (2004). Duane's Clinical Ophthalmology, Lippincott Williams & Wilkins.
7. Raasch, T. W., Bailey, I. L., Bullimore, M. A. (1998). Repeatability of visual acuity measurement. Optometry and Vision Science, 75(5), 342-348.
8. Dalimier, E., Pailos, E., Rivera, R., and Navarro, R. (2009). Experimental validation of a Bayesian model of visual acuity. Journal of Vision, 9(7), 1–16.
9. Ling, N., Rao, X., Wang, C., Yu, X., Hu, Y. (2005). Hartmann-Shack wavefront sensor for the human eye aberration. SPIE Proceedings, 6018, 60180.