Fizikai Tudományok Doktori Iskola 

BME TTK, Atomfizika Tanszék

Témavezető: Dr. Erdei Gábor

Humán látásélesség elméleti és kísérleti vizsgálata, modellezése numerikus szimulációval

A kutatási téma néhány soros bemutatása

Szürkehályog (cataracta) esetén a szemben nagyfokú fényszórás lép fel, mely szélsőséges esetben vakságot okozhat. A betegség intraokuláris műlencsék (IOL) műtéti beültetésével kezelhető. A klinikai gyakorlatban alkalmazott műlencsék azonban nem tudnak a valódi szemlencséknek minden jellemzőben egyszerre maradéktalanul megfelelni. Legfontosabb hiányosságuk, hogy nem képesek akkomodációra, illetve színhiba-korrekcióra, ami miatt növekvő igény mutatkozik a képminőség javítására [1]. Ennek megfelelően a gyártók folyamatosan fejlesztik termékeiket, és egyre több erőforrást fordítanak az egyedi, személyre szabott műlencsék precíz tervezésére és a lencse paramétereinek optimalizálására. Ezért fontos feladat, hogy az optikai tervezésben használatos objektív mérőszámokat párhuzamba lehessen állítani a szemészorvosok által használt, az érzékelt látásminőséget jellemző visusértékkel [2, 3].

 

A kutatóhely rövid bemutatása

Kutatómunkámat a BME Atomfizika Tanszék ipari partnere, a Medicontur Orvostechnikai Kft. által vezetett, 2014-ben indult „A szürkehályog hatékony gyógyítását elősegítő orvostechnikai kutatás-fejlesztések” című VKSZ-12-1-2013-80 projekthez kapcsolódóan végzem, a Semmelweis Egyetem szemészorvosaival szoros együttműködésben. A projekt fő célja a szürkehályogban szenvedő betegek részére olyan intraokuláris lencsék kifejlesztése, amelyek a jelenlegi megoldásoknál komfortosabb látásérzetet biztosítanak.

 

A kutatás történetének, tágabb kontextusának bemutatása

Az első IOL-k megjelenésekor a szürkehályog még tipikusan időskori megbetegedésnek számított, emellett a páciensek számára tökéletesen megfelelt a fix fókusztávolság és a színhiba-korrekció nélküli, szférikus lencsefelületek használatával elérhető képminőség. Ezzel szemben napjainkban a cataracta már népbetegség, az aktív munkavégző generációt is egyre jobban érinti. Ennek megfelelően a műlencsék segítségével a látási hibák minél jobb korrekcióját kell megvalósítani, sőt a távollátáshoz beállított IOL esetén közelre nézéshez alkalmazandó szemüveg elhagyása is szükségessé vált. A műtéti tapasztalatok alapján emellett fiziológiai szempontok is felmerültek: a szemészorvosok egyre kisebb sebet ejtenek a gyors gyógyuláshoz, valamint a műtét utáni komplikációk csökkentése érdekében [1].

A látványos fejlődés eléréshez azonban nem elegendő a műlencsék paramétereinek javítása, optimalizálása, mert a szem optikai leképezésén kívül a neurális transzfer és additív zajok is befolyásolják azt az agykérgen kialakuló reprezentációt, amelyet végül a páciens felismer. Ennek megfelelően a hiteles eredmények elérése érdekében az érzékelt látásélességet meghatározó teljes, a képalkotástól a karakterfelismerésig terjedő folyamatnak a vizsgálata, modellezése szükséges (lásd 1. ábra) [2, 3, 4, 8]. A klinikai beavatkozás hatásfokának meghatározása a pre- és postoperatív visusértékek között mérhető javulás alapján történik, melyhez a standard klinikai teszteknél pontosabb eljárás szükséges. Így a kutatás-fejlesztésnek a lencsetervezésen túl ki kell terjednie a látás teljes folyamatának modellezésére és a mérési eljárásokra is [5, 6].

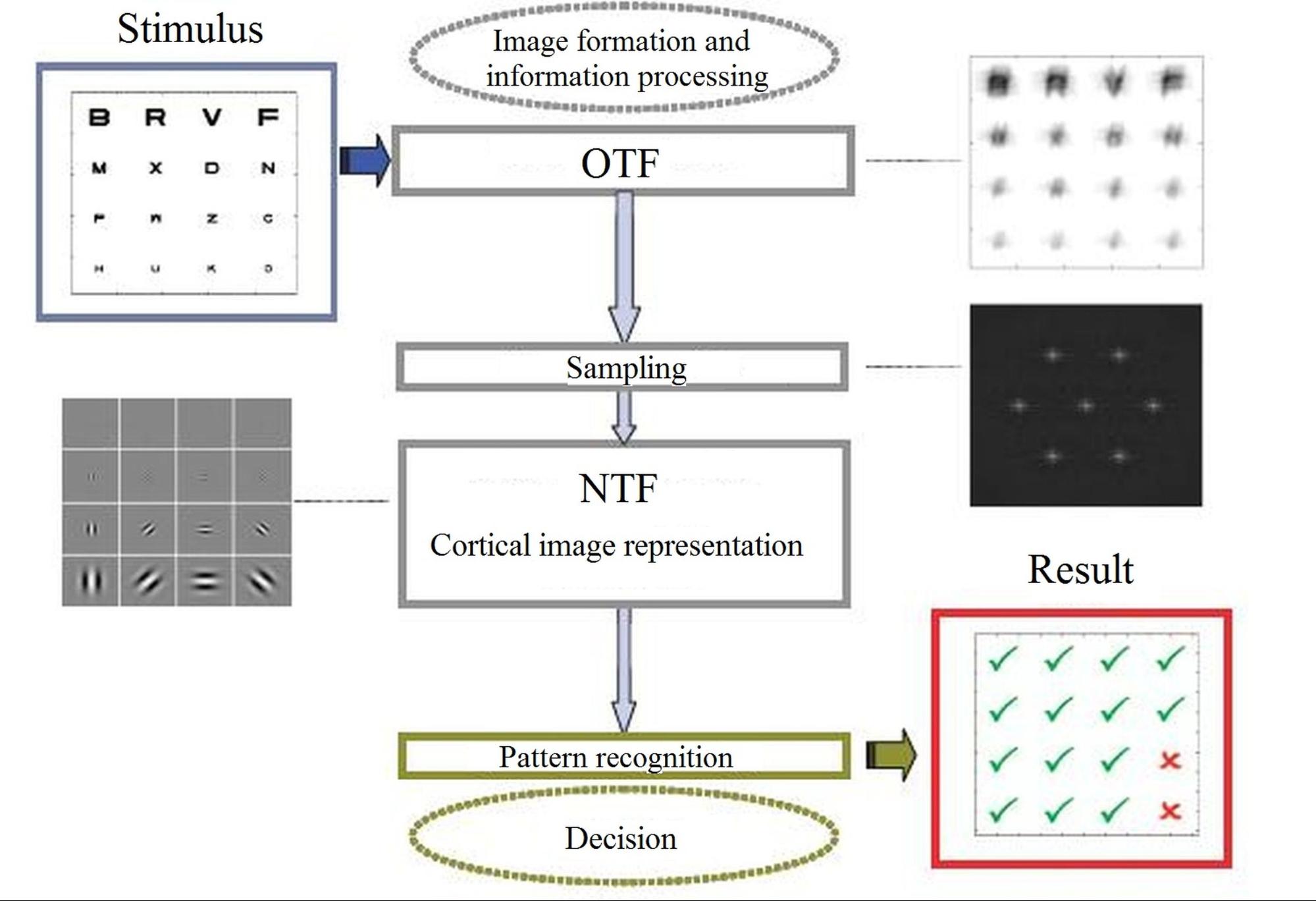
1. ábra: A humán látásélességet meghatározó legfontosabb lépések: optikai képalkotás, neurális átvitel, additív zaj és kortikális karakterfelismerés [8]

 

A kutatás célja, a megválaszolandó kérdések

A kutatás hazai konzorciumi együttműködés keretében valósult meg, melynek elsődleges célja a beültetendő műlencsék segítségével elérhető képminőség javítása a minél jobb látásérzet biztosítása érdekében. Ehhez elengedhetetlen a humán látásélességet befolyásoló paraméterek feltérképezése és hatásuk részletes elemzése. Feladatom egy olyan neurofiziológiai látásmodell kidolgozása, mely az emberi szem optikai leképezési paraméterein túl figyelembe veszi az idegrendszeri jelfeldolgozás tulajdonságait és helyesen leírja a kortex által végzett karakterfelismerést is. Egy ilyen látásmodell segítségével az optikai tervezés (pl. műlencsetervezés) során közvetlenül a látásélességre lehetne optimalizálni az optikai mérőszámok maximalizálása helyett. A modell kalibrálása és ellenőrzése érdekében a szimulált visusértéket össze kell vetni valós látásélesség-vizsgálatok eredményével is. A standard klinikai mérések azonban relatíve magas ismétlési hibával rendelkeznek [5, 7], így ezek nem alkalmasak a kalibráció elvégzésére. A pontos, szisztematikus hibamentes és minimális bizonytalanságú visusmeghatározáshoz ezért új mérési és kiértékelési eljárás kidolgozására van szükség. Az ideális módszer úgy csökkenti a véletlen hibát, hogy közben nem terheli offsettel az eredményeket. Célom egy olyan mérési protokoll kidolgozása, mely megfelel a klinikai standardnak, s így a kutatás mellett a mindennapi orvosi gyakorlatban is alkalmazható. Az új módszer segítségével lehetőség nyílik nagy pontosságú látásélesség-tesztek végzésére, ami növeli a mérések megbízhatóságát és összehasonlíthatóságát.

 

Módszerek

Az általam fejlesztett látásmodell elsődleges feladata, hogy meghatározza az emberi szem leképezőrendszerének leírására szolgáló, jól mérhető optikai paraméterek és az orvosok által a klinikai gyakorlatban használt, az érzékelt látásélességet megadó visusérték közötti összefüggést. Az irodalomban található visusmodellek leggyakrabban az optikai úthosszkülönbséggel jellemzett hullámfront-aberrációt alkalmazzák, mint bemeneti paramétert, mert ez egyszerre jellemzi a szem összes monokromatikus képalkotási hibáját, valamint mértéke Shack-Hartmann szenzorral egyszerű rutinvizsgálattal meghatározható (lásd 2. ábra) [2, 3, 9]. Ezek a modellek azonban meglehetősen egyszerű monokromatikus optikai transzfert valósítanak meg, mely nem elég precíz a műlencsetervezéshez. Emiatt én a látásmodellemet egy optikai tervezőrendszerben implementált, fiziológiailag pontos szemmodellre építettem, melynek segítségével a színhiba is figyelembe vehető.

 

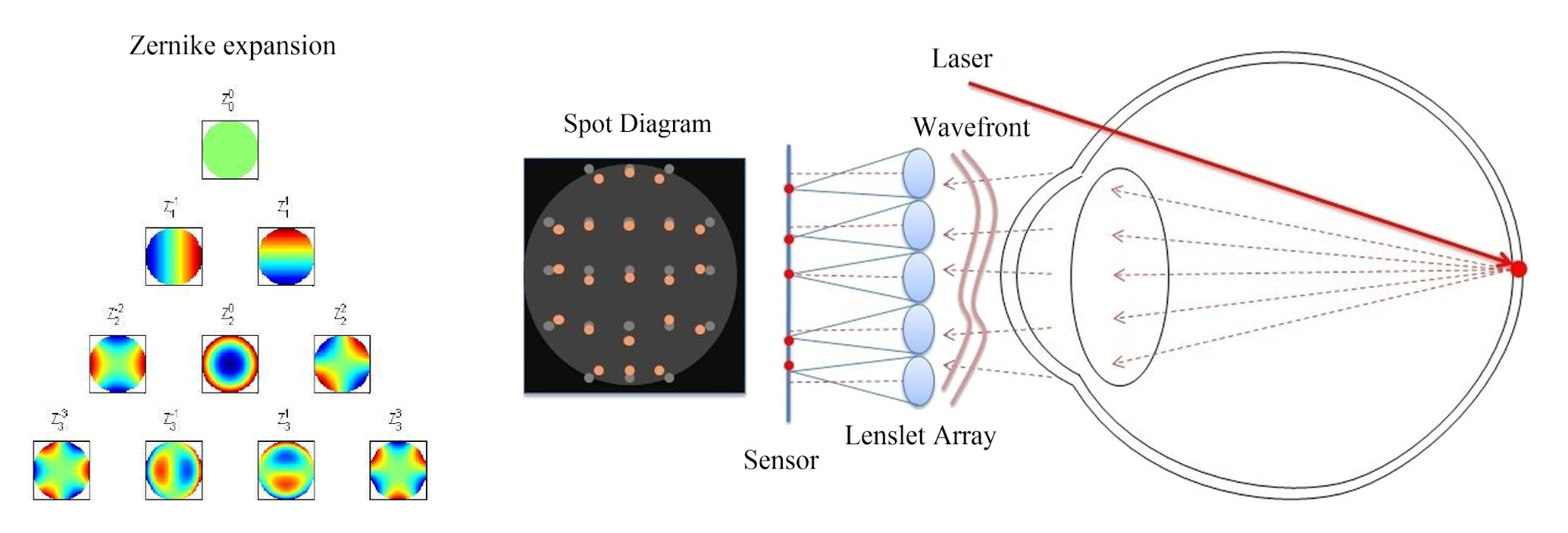
2. ábra: Shack-Hartmann szenzorral végzett hullámfront-aberráció mérés [9]

 

A humán látásélesség pontos modellezéséhez és szimulációjához a bemeneti paraméterek helyes megválasztása és szabatos mérése mellett elengedhetetlen egy hatékony képfeldolgozó algoritmus megvalósítása. Mivel a biológiai rendszerek lineáris tulajdonsággal rendelkeznek, így a szem által végzett optikai leképezést és a neurális transzfert modellező folyamatokat Fourier-térben implementáltam, ahol a konvolúciós számítások közönséges szorzássá egyszerűsödnek. Továbbá az eredmények effektív kiértékelése érdekében bevezettem egy új pontozási módszert, mely jelentős mértékben csökkenti a véletlen hibát [S1, S2].

A hagyományos visusvizsgálatok során a páciens feladata a látásvizsgáló táblán elhelyezkedő egyre csökkenő méretű betűk helyes azonosítása. A klinikai gyakorlatban az orvos csak azt ellenőrzi, hogy a páciens helyesen felismerte-e az adott karaktert vagy sem, s ez alapján határozza meg a visus értékét. Bizonyos esetekben azonban a vizsgáló eltekint a kisebb hibáktól, úgymint a C és O, vagy P és F betűk összetévesztése, mely azt sugallja, hogy a látás nem írható le pontosan egy egyszerű bináris (helyes/helytelen) reprezentációval. Ennek megfelelően munkám során kidolgoztam egy lényegesen több információt szolgáltató pontozási algoritmust. Definiáltam az ABC nagybetűinek korrelációját, melynek segítségével figyelembe vehető, hogy mennyire eltérő betűnek azonosította a páciens az adott karaktert, s így számszerűsíthető a tévesztés mértéke is, nem csak maga a tévesztés ténye. A korreláció értékét a betűk képének Pearson-féle keresztkorrelációja alapján úgy számszerűsítettem, hogy az eredmény közvetlenül összehasonlítható legyen a konvencionális bináris pontozással [S1, S2]. Az angol ABC nagybetűinek korrelációján alapuló pontozási rendszert a 3. ábra szemlélteti.

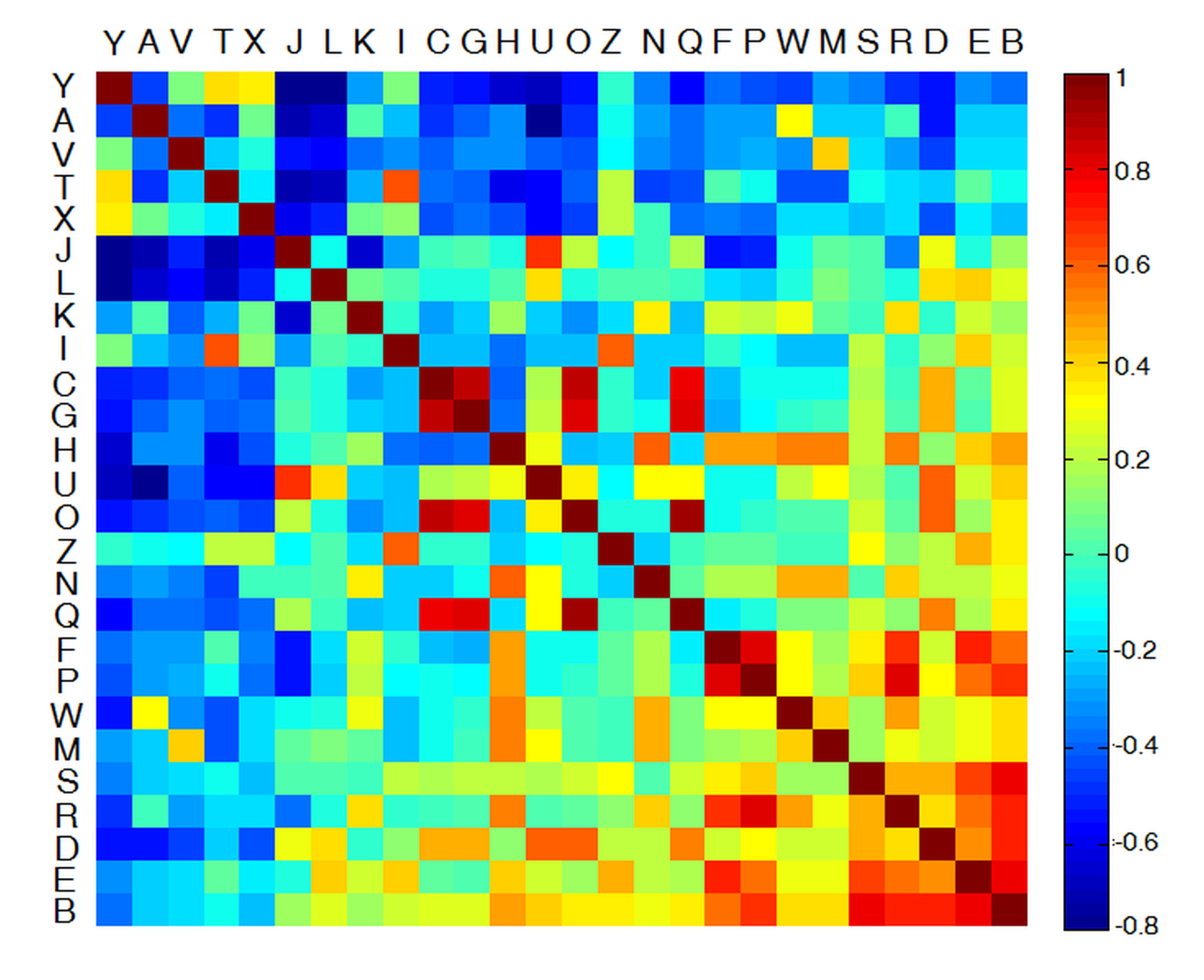
3. ábra: Az általam bevezetett, betűk korrelációján alapuló kiértékelés szemléltetése. A bal felső sarokban az egymással nehezen összetéveszthető betűk helyezkednek el, míg a jobb alsó sarok felé a karakterek korrelációja nő

 

Eddigi eredmények

Kutatómunkám során megvalósítottam egy olyan neurofiziológiai látásmodellt, amely egy fiziológiailag pontos szemmodellre épül, valamint figyelembe veszi a neurális rendszer jelátviteli tulajdonságait és a vizuális kéreg felismerésben játszott szerepét is [S4]. A modell bemenete a páciens szemének hullámfront-aberrációja és pupillájának átmérője, mely alapján a szemmodellben meg lesz határozásra az egyedi polikromatikus pontszórásfüggvény (lásd 4. ábra), amely a retina síkjában kialakuló optikailag szűrt képet definiálja.

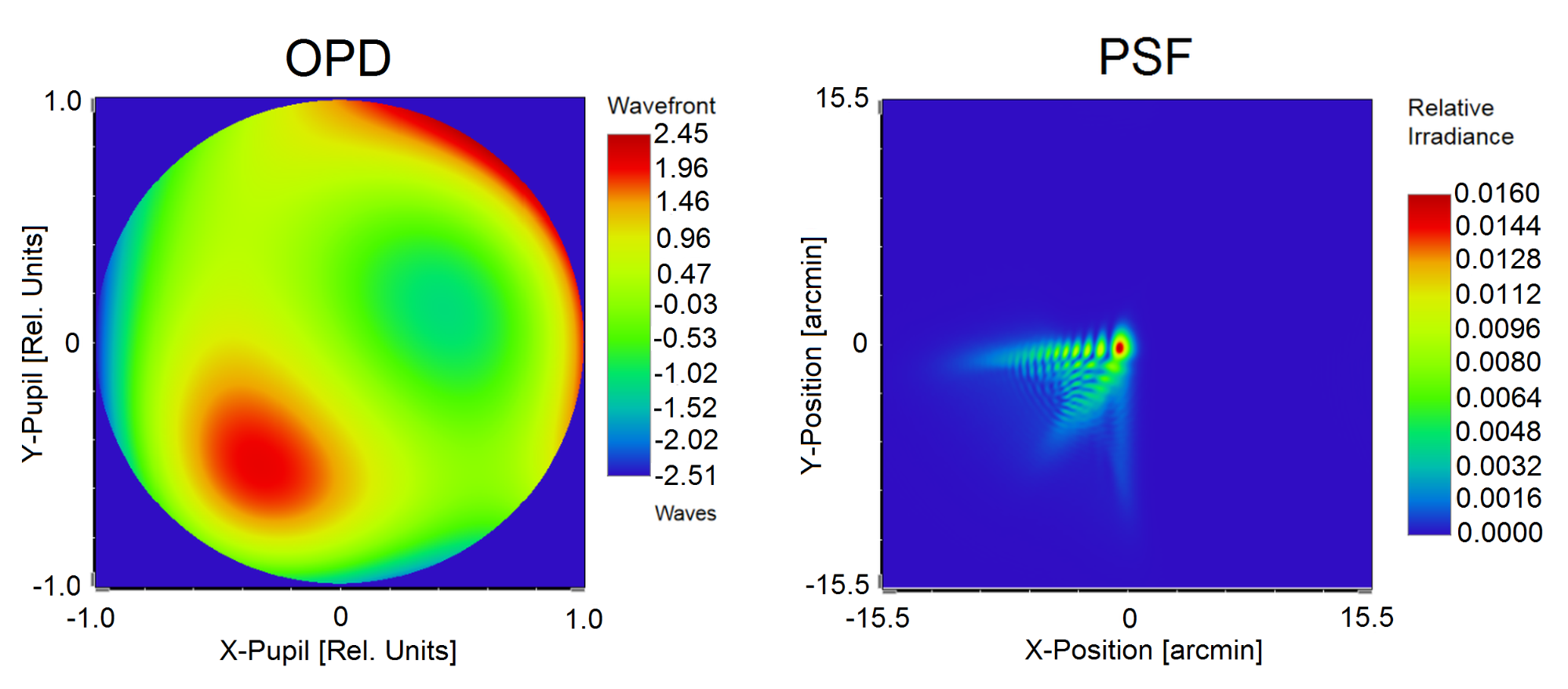
4. ábra: A polikromatikus pontszórásfüggvény (PSF) meghatározása az optikai úthosszkülönbséggel (OPD) jellemzett hullámfront-aberráció mérése alapján a fiziológiailag pontos szemmodellemben

 

A standard látásélesség-vizsgálatok elvégzésének előfeltétele az angol ABC ismerete, s így a teszt nem végezhető el kisgyermekeken és írástudatlan pácienseken. Ezzel szemben az objektív mérésen alapuló bemenetnek köszönhetően személyre szabott látásélesség-szimulációk végezhetők minden vizsgált alanyra. Mivel a neurális teljesítőképesség mérésére nincs olyan, az orvosi gyakorlatban széles körben használt, könnyen kivitelezhető, objektív mérési módszer, mint amilyen a hullámfrontszenzor alkalmazása az optikai aberrációk meghatározására, ezért a neurális jelfeldolgozás az irodalomban bemutatott eljárásoknak megfelelően, átlagos egészséges páciensre vonatkozó adatok alapján mindenkire egységesen történik [3, 4]. Ezt követi a neurális zaj modellezése, mely az idegrendszer teljesítőképességének időbeli, valamint egyének közötti változásait, bizonytalanságait írja le. A képfeldolgozás egyes lépéseinek hatását szemlélteti az 5. ábra, melynek végeredménye a kép zajjal terhelt agykérgi reprezentációja, melyet a páciens fel szeretne ismerni.

5. ábra: Az általam fejlesztett neurofiziológiai látásmodell legfontosabb képfeldolgozó lépéseinek szemléltetése: a) eredeti kép, b) optikai leképezés, c) neurális jelfeldolgozás, d) zajos agykérgi reprezentáció

 

Az egyedi visusszimulációk mellett a modell segítségével lehetőség nyílik a látásélesség minőségét befolyásoló környezeti tényezők hatásának osztályozására, rangsorolására, valamint az általuk okozott mérési hiba szimulációkon keresztül történő elemzésére és számszerűsítésére is. Eredményeim alapján a környezeti paraméterek közül a vizsgálószoba megvilágítása és ezzel együtt a pupilla mérete befolyásolja legnagyobb mértékben a látásminőséget, ami összhangban van az irodalomban bemutatott eredményekkel [5, 6]. Megállapíthatóvá vált továbbá a mérések standardizálásának szükségessége, illetve azok pontossága ismételhetőség szempontjából.

A modell kalibrálása érdekében nagy pontosságú visusvizsgálatokat végeztem egy saját fejlesztésű mérőrendszerrel. A pupillaméret látásélességre gyakorolt jelentős hatása miatt úgy egészítettem ki a rendszert, hogy a pupilla látásteszt közben, valós időben is folyamatosan monitorozható legyen [S3]. A mérési elrendezést a 6. ábra szemlélteti.

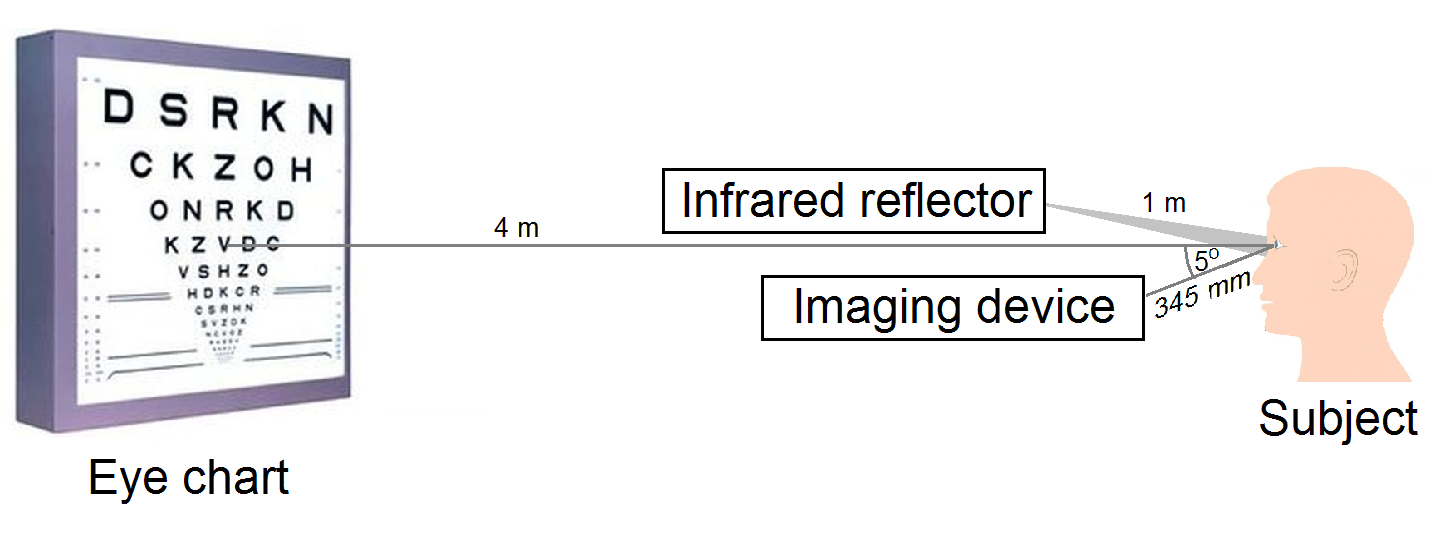
6. ábra: Mérési elrendezés a pupilla átmérő monitorozására látásélesség-vizsgálatok közben

 

A felvételek kiértékelése céljából kidolgoztam egy Hough-transzformáción alapuló algoritmust, mely az iris külső átmérőjét használja referenciának a páciens mozgásából származó nagyítási hiba kiküszöbölésére (lásd 7. ábra). Eredményeim alapján a pupillamérés érzékenysége meghaladja a kereskedelmi forgalomban kapható távoltéri rendszerek pontosságát, és megfelelő adatokat szolgáltat látásélesség-szimulációk végzéséhez [S3].

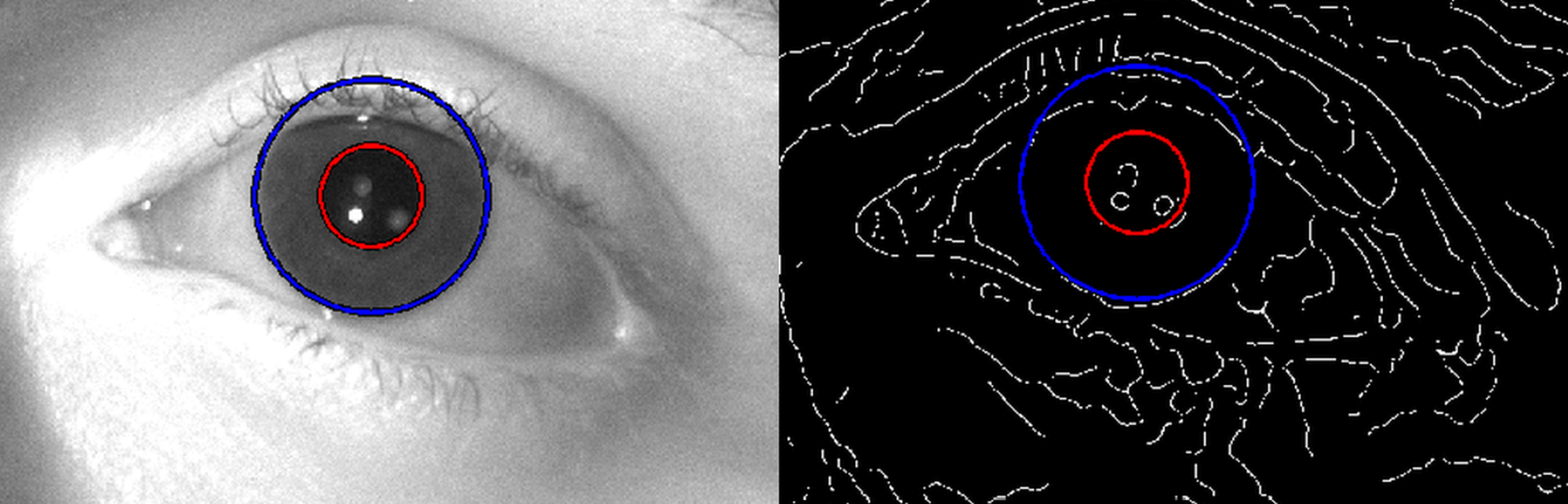
7. ábra: A pupilla átmérőjének meghatározása az iris mérete, mint referencia alapján a Hough- transzformáción alapuló algoritmusommal, melynek segítségével kiküszöbölhető a páciens mozgásából eredő nagyítási hiba

 

A szimuláció és a kísérleti elrendezéssel végzett precíz mérés eredményeinek összehasonlító elemzése jó egyezést mutatott, ami alátámasztja a látásmodell alkalmazhatóságát. Továbbá, a kalibrációs csoporton végzett vizsgálatok alapján a szimulációk maradék hibája lényegesen kisebb a standard visustesztek ismétlési hibájánál [S4]. A mérési eljárás felhasználhatóságának kiterjesztése érdekében a protokoll kisebb módosításával kidolgoztam egy olyan módszert, mely megfelel a klinikai szabványnak, így a mindennapi szemészeti gyakorlatban is kivitelezhető, a hagyományos mérésnél pontosabb látásélesség-vizsgálatot tesz lehetővé [S5]. A többféle mérési összeállításban végzett kísérletek és a modellel végzett szimulációk alapján megállapítható, hogy a betűk keresztkorrelációján alapuló pontozási rendszer segítségével a kiértékelés bizonytalansága a visusteszt paramétereitől függően 20-30%-kal csökkenthető [S2, S5].

 

Várható impakt, további kutatás

A betűk korrelációján alapuló pontozási rendszer segítségével a kutatásban, valamint a klinikai gyakorlatban a szemészeti standardnak megfelelő, de a hagyományos eljárásnál lényegesen pontosabb mérések végzésére nyílik lehetőség. Az általam kidolgozott neurofiziológiai látásmodell segítségével visusszimulációk végezhetők, mely lehetőséget biztosít az optikai tervezés során közvetlenül látásélességre történő optimalizálásra akár személyre szabott, akár átlagos modell segítségével. Mivel a módszer objektív mérésen alapul, így kiterjedt mintahalmazon végzett klinikai kalibrációt követően alternatív látásminőség-vizsgálati módszert biztosíthat kisgyermekek és írástudatlanok számára is. Továbbá a lecsökkentett mérési hiba következtében a szimulációs algoritmus alkalmas lehet cataracta műtét utáni látásélesség pontos prediktálására, ami nagymértékben elősegíti az egyedi lencsetervezést.

 

Saját publikációk, hivatkozások, linkgyűjtemény

Kapcsolódó saját publikációk listája.

S1. Erdei G., Fülep Cs. (2018). Measuring visual acuity of a client. World Intellectual Property Organization, WO/2018/020281 A1, PCT/HU2016/000050.

S2. Fülep Cs., Kovács I., Kránitz K., Erdei G. (2017). Correlation-based evaluation of visual performance to reduce the statistical error of visual acuity. Journal of the Optical Society of America A, 34(7), 1255–1264.

S3. Fülep Cs., Erdei G. (2017). Far-field infrared system for the high-accuracy in-situ measurement of ocular pupil diameter. IEEE Proceedings of the 10th International Symposium on Image and Signal Processing and Analysis, 31–36.

S4. Fülep Cs., Kovács I., Kránitz K., Erdei G. (2018). Simulation of visual acuity by personalizable neuro-physiological model of the human eye, Scientific Reports, benyújtva. 

S5. Fülep Cs., Kovács I., Kránitz K., Nagy Z. Zs., Erdei G. (2018). Application of correlation-based scoring scheme for visual acuity measurements in the clinical practice. Translational Vision Science & Technology, benyújtva.

 

Linkgyűjtemény.

Medicontur Orvostechnikai Kft.

BME Atomfizika Tanszék

Semmelweis Egyetem, Szemészeti Klinika

Cataracta

Visus

Pontszórásfüggvény

Hough-transzformáció

 

Hivatkozások listája.

1. Jinabhai, A. N., Young, G., Hall, L. A., Wolffsohn, J. S. (2013). Clinical techniques to assess the visual and optical performance of intraocular lenses: a review. In D. Navarro (Ed.), Cataracts and cataract surgery: types, risk factors, and treatment options. Eye and vision research development, Nova science.
2. Nestares, O., Navarro, R., Antona, B. (2003). Bayesian model of Snellen visual acuity. Journal of the Optical Society of America A, 20, 1371–1381.
3. Watson, A. B., Ahumada, A. J. Jr. (2008). Predicting visual acuity from wavefront aberrations. Journal of Vision, 8(4):17, 1–19.
4. Watson, A. B., Ahumada, A. J. Jr. (2015). Letter identification and the Neural Image Classifier. Journal of Vision, 15(2):15, 1–26.
5. Rabbetts, R. B. (2007). Bennett and Rabbetts’ Clinical Visual Optics. Butterworth-Heinemann, Elsevier.
6. Duane, T. (2004). Duane's Clinical Ophthalmology, Lippincott Williams & Wilkins.
7. Raasch, T. W., Bailey, I. L., Bullimore, M. A. (1998). Repeatability of visual acuity measurement. Optometry and Vision Science, 75(5), 342–348.
8. Dalimier, E., Pailos, E., Rivera, R., and Navarro, R. (2009). Experimental validation of a Bayesian model of visual acuity. Journal of Vision, 9(7), 1–16.
9. Ling, N., Rao, X., Wang, C., Yu, X., Hu, Y. (2005). Hartmann-Shack wavefront sensor for the human eye aberration. SPIE Proceedings, 6018, 60180.