|
|
BMe Kutatói pályázat |
|
Villamosmérnöki Tudományok Doktori Iskola
BME-VIK, Hálózati Rendszerek és Szolgáltatások Tanszék
Akusztikai és Stúdiótechnikai Laboratórium
Témavezető: Dr. Fiala Péter
Hangtérszintézis az átlapolódási jelenségek elkerülésével
A kutatási téma néhány soros bemutatása
A hangtérszintézis (Wave Field Synthesis: WFS) egy olyan korszerű térhangzást biztosító technika, mellyel kiterjedt megfigyelési területen tetszőleges hangtér fizikai jellemzői (pl. nyomáseloszlása) visszaállíthatók a megfigyelési terület határán elhelyezett hangszóró-sokaság megfelelő vezérlésével. A technika alkalmazásával gyakorlatilag egy „akusztikus hologram” hozható létre, ezzel elkerülve a sztereofon rendszerek (Dolby 5.1, Atmos stb.) közös hátrányát, miszerint ezek az egyes hangtérjellemzőket egyetlen pontban, a sweet spotban képesek visszaállítani.

1. ábra: A hangtérszintézis alapfeladata
A kutatóhely rövid bemutatása
Kutatásomat a BME HIT tanszék Akusztikai és Stúdiótechnikai Laboratóriumában végzem. Csoportunk az akusztika számos területén végez elismert kutató-, fejlesztőmunkát, így pl. a numerikus akusztika, akusztikai jelfeldolgozás, épület- és talajrezgések vizsgálatának témakörében. Emellett komoly eszközparkkal és tapasztalattal rendelkezik mind helyi, süketszobában végzett, mind terepi zaj- és rezgésmérések elvégzéséhez.
A kutatás történetének, tágabb kontextusának bemutatás
Habár a sok hangszórós fizikai alapú reprodukció alapötlete már az 1930-as években megjelent, a Wave Field Synthesis technika alapjait a 90-es évek elején fektették le Delfti Egyetemen [1-4], ekkorra vált ugyanis elérhetővé a nagyszámú hangszórót alkalmazó rendszer kompakt megvalósítása és valós idejű vezérlése. Azóta a módszer folyamatos kutatás és fejlesztés alatt áll [5-7], az elmúlt években már több kereskedelmi forgalomban kapható WFS alapú hangrendszer is megjelent.

2. ábra: Az IOSONO, kereskedelmi forgalomban kapható WFS rendszer a Los Angeles-i Mann’s Chinese Theatre-ben
Jelenlegi, a WFS elméleti alapjait érintő kutatásomat 2009-ben kezdtem MSc hallgatóként; a technika zárt terekben való alkalmazásának vizsgálatával intézményi TDK I. helyezést, országosan III. helyezést, valamint több diplomaterv-pályázaton helyezést elérve. Doktori tanulmányaim során kutatásom középpontjában kezdetben a mozgó hangforrások terének visszaállítása állt [FG1-3], valamint magam is jelentősen hozzájárultam a módszer elméleti alapjainak kifejlesztéséhez egy egységesített hangtérszintézis-elmélet kidolgozásával [FG4,FG5]. Utóbbi kutatás egy részét a 2017. évi Új Nemzeti Kiválóság Program keretein belül végeztem. Az általam kidolgozott elméleti keretrendszer az elmúlt évek során több prominens nemzetközi kutatócsoport által végzett kutatás kiindulási alapjaként szolgált [8,9], és mára általánosan elfogadottá vált [10]. Emellett módszerem jelenleg is implementálás alatt áll egy nyílt forráskódú német fejlesztésű WFS MATLAB toolbox-ban.
A kutatás célja, a megválaszolandó kérdések
Az általam létrehozott elméleti keretrendszer lehetővé teszi a hangtér-reprodukció járulékos hatásainak analitikus leírását és kompenzációját is. Ezek a járulékos hatások az idealizált fizikai modell gyakorlatba való átültetése során történő megsértéséből erednek: az ideálisan folytonos pontforrás-eloszlás helyett egymástól véges távolságban elhelyezett hangszórókat alkalmazunk a szintézishez. Ez a létrehozott hangtér jól hallható torzulásához, színeződéséhez vezet. A jelenséget térbeli átlapolódásnak nevezzük, és az egyes hangszórókból származó különálló, másodlagos hullámfrontok hatásaként értelmezhetjük [11].
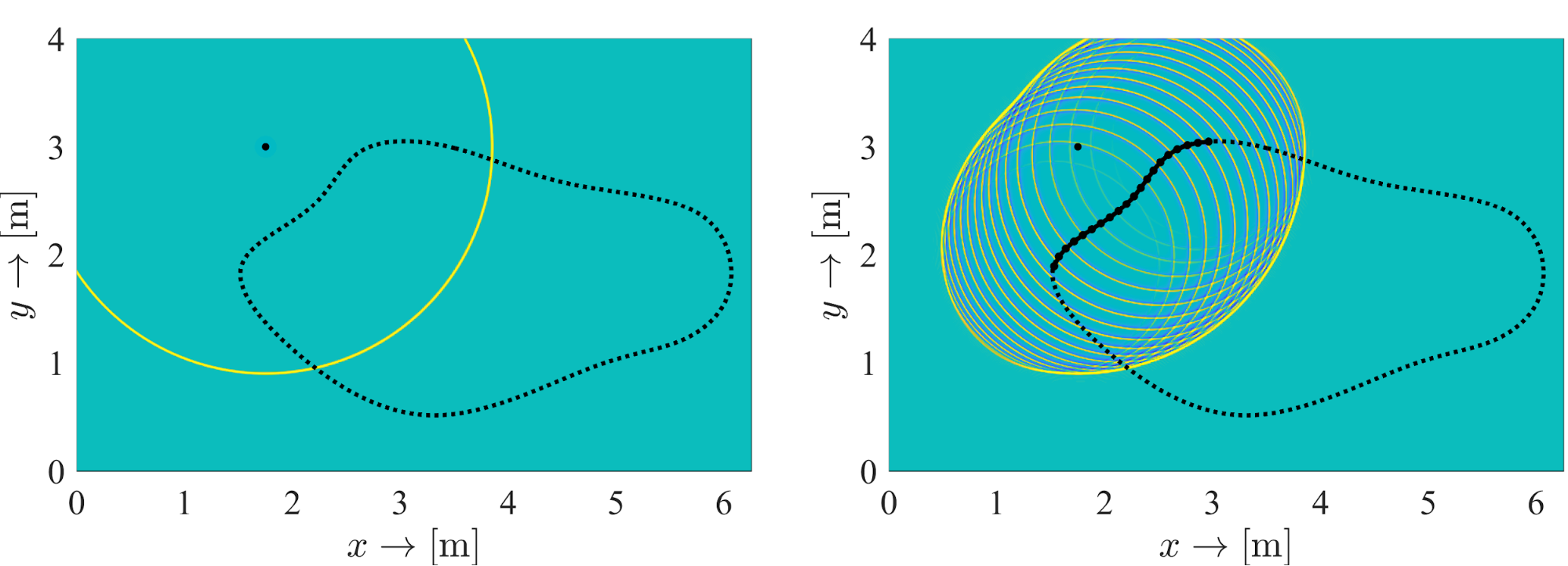
3. ábra: Átlapolódási jelenségek a hangtérszintézisben impulzus gerjesztésű virtuális forrás esetén. A bal ábrán a szintetizálandó célhangtér, a jobb ábrán a reprodukált hangtér látható a hangszórók közötti távolságból eredő térbeli átlapolódás jelenlétében. A szintézishez használt hangszórók pozícióját szaggatott vonal jelzi
Jelen kutatásom célja a korábbi eredményeim felhasználásával ezen jelenségek leírása és kiküszöbölése. Munkám során megvizsgálom, hogy milyen analitikus eszközökkel tárgyalható a térbeli átlapolódás, milyen módszerrel szüntethetők meg az átlapolódó komponensek, és ez milyen hatással van a szintézis eredményére.
Módszerek
A diszkrét hangszóró-eloszlás hatásának leírására gyakran alkalmazott módszer a szintetizált tér és a vezérlőfüggvények tér-frekvenciatartománybeli (azaz térbeli Fourier transzformáltjának) vizsgálata [6]. Munkám során az ún. stacionárius fázis módszert alkalmazom e spektrális integrálformulák aszimptotikus közelítésére. A módszer segítségével azonosítható, hogy adott frekvencián a hangszóró-eloszlás mely elemei járulnak hozzá a térbeli átlapolódás kialakulásához. Az átlapolódást okozó hangszórók elnémításával az átlapolódási jelenségek megszüntethetők, természetesen a szintetizált tér torzulásának árán.
A kidolgozott analitikus módszert MATLAB környezetben numerikus szimulációs eszközökkel vizsgálom és tesztelem. A későbbiekben az eredmény a laboratóriumunkkal jó munkakapcsolatban álló Rostocki Egyetem Akusztikai Laboratóriumában elérhető WFS installáción, valós hardveren is kipróbálható. Ugyanezen rendszeren a módszer virtuálisan is tesztelhető, ugyanis rendelkezésre áll a rendszer HRTF adatbázisa, amely binaurális visszajátszást tesz lehetővé [12].
Fontos megjegyezni, hogy a feladat más szempontból is megközelíthető. A kutatásommal párhuzamosan a rostocki kutatócsoport szintén a saját, korábban kidolgozott elméleti keretrendszeremre támaszkodva ugyanezt a problémát pusztán a tértartományban közelíti meg, a szintetizált teret leíró konvolúciós integrál aszimptotikus kiértékelésével. Az ebből a kutatásból készülő, beküldés előtt álló publikáción társszerzőként fogok szerepelni [13].
Eddigi eredmények
A fent leírt módszerrel, tehát a szintézist leíró spektrális integrálegyenletek aszimptotikus kiértékelésével egyszerű analitikus leírást adtam a térbeli átlapolódási jelenségek forrására egy adott frekvencián. A leírás segítségével meghatározható minden forráselemre (hangszóróra) egy határfrekvencia, amely fölött az adott hangszóró térbeli átlapolódási jelenségek forrása lesz. Az egyes hangszórók vezérlőjelének erre a térbeli átlapolódási frekvenciára való sávkorlátozásával az átlapolódási jelenségek megszüntethetők. Ezzel tehát egyszerűen implementálható, hatékony módszert adtam a probléma megoldására [FG6].
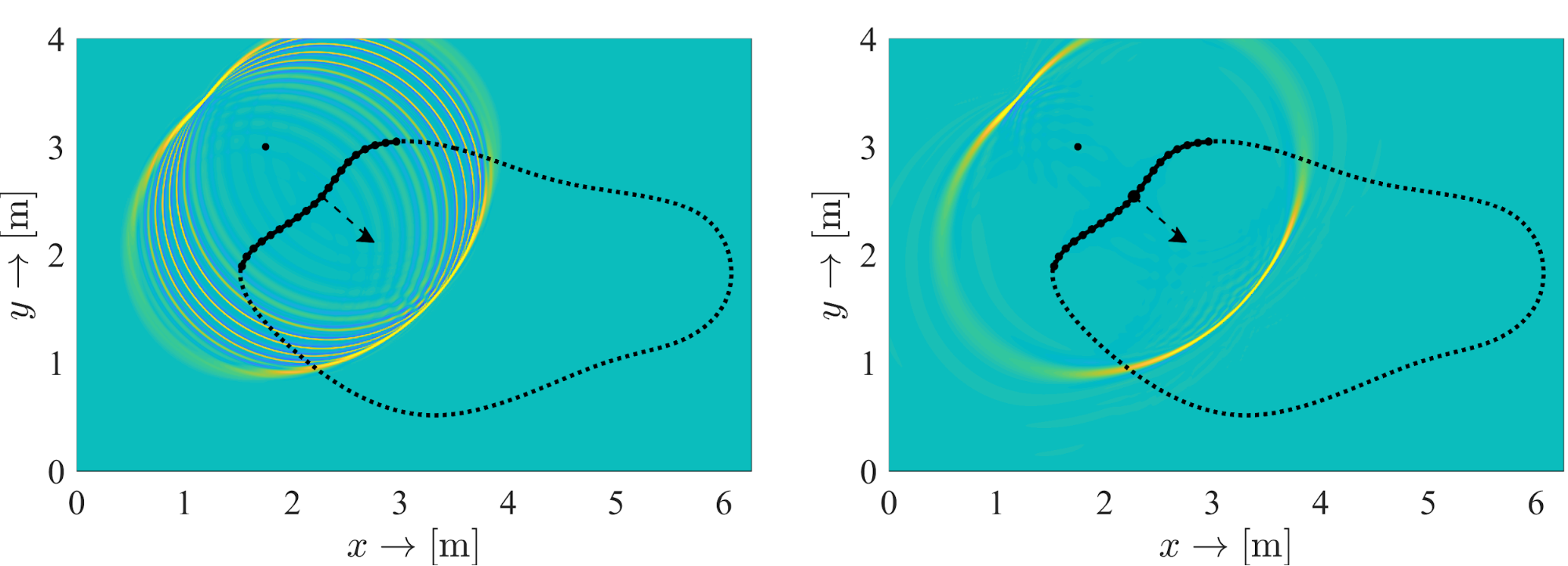
4. ábra: A szintézis eredménye ideális átlapolódás elleni szűréssel (bal ábra) és a szűrés mellett ideálisan irányított hangszórók alkalmazásával (jobb ábra)
Az 4. ábra bal oldalán a módszerem eredménye látható. Megfigyelhető, hogy a módszer alkalmazásával egy kitüntetett irányban tökéletes, átlapolódási jelenségek nélküli hullámfront-visszaállítás lehetséges. Ezt az irányt az ábrán fekete nyíl jelzi.
Látható, hogy még ideális átlapolódás elleni szűrés alkalmazása mellett is, az ettől az
iránytól eltérő orientációjú hullámok mögött továbbra is jelen vannak másodlagos, átlapolódásból származó hullámfrontok. Ezek a hullámok egyszerű jelfeldolgozási eszközökkel nem szüntethetők meg, hatásuk kizárólag irányított hangszórók alkalmazásával eliminálható. Ugyancsak az általam alkotott keretrendszer segítségével adtam egy analitikus formulát az ideális hangszóró-iránykarakterisztika meghatározására, amely segítségével ezek a fennmaradó átlapolódási jelenségek megszüntethetők. Ennek eredményét mutatja a 4. ábra jobb oldala.
Doktori tanulmányaim kezdetén kutatásom középpontjában mozgó hangforrások által keltett hullámterek szintetizálása állt. Ebben a dinamikus, idő-variáns esetben a fő feladat a Doppler-hatás megfelelő visszaállítása. A témából számos publikációm született [FG1,FG2], kiterjesztve a WFS elméletemet tetszőleges trajektórián mozgó hangforrások szintézisére is [FG3].
Egy korábbi konferenciaközleményben megmutattam, hogy a térbeli átlapolódási jelenségek fokozottabban, kifejezettebben jelentkeznek mozgó források szintézise esetén, mivel az átlapolódó, másodlagos hullámfrontok más Doppler-tolást szenvednek, mint az eredeti virtuális forrás hullámfrontja [FG8]. Ennek elkerüléséhez általánosítottam az előzőleg meghatározott átlapolódás-elleni szűrő határfrekvenciáját mozgó források szintézisére is, amely egy idővariáns határfrekvencia definiáláshoz vezetett. A módszer eredménye az 5. ábrán látható.
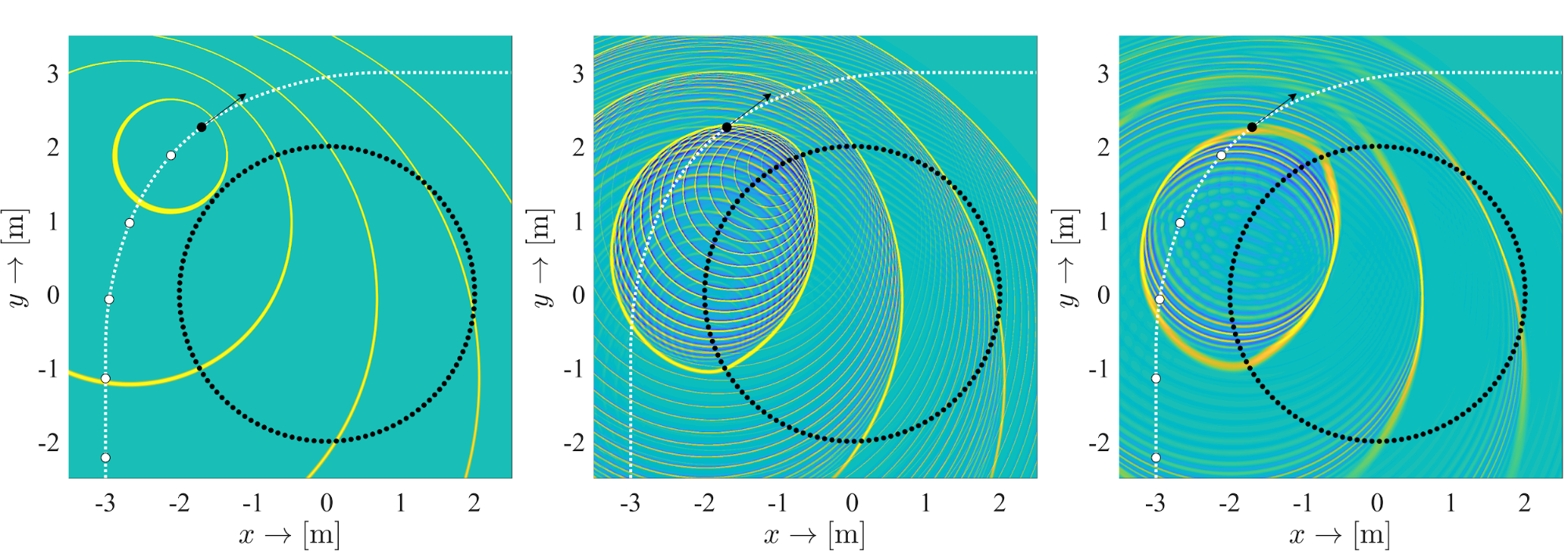
5. ábra: Mozgó forrás szintézise kör alakú hangszóróeloszlással, a célhangtérrel (bal ábra), a szintetizált, átlapolódó térrel (középső ábra) és ideális átlapolódás elleni szűréssel (jobb ábra)
Várható impakt, további kutatás
Bár a kezdeti eredményeket ez év tavaszán, egy nemzetközi konferencián bemutattam [FG7,FG8], a módszer teljes kidolgozása és impakt faktoros folyóiratban való publikálása még hátralévő feladat. Az ehhez szükséges részfeladatok közé tartozik még az átlapolódásmentes szintézis iránya (4. ábrán fekete nyíl) változtatásának vizsgálata, illetve a módszer szubjektív validációja is meghallgatásos tesztek segítségével. Módszerem egyszerű, könnyen implementálható megoldást ad egy, a hangtérszintézis megjelenése óta fennálló problémára, így a témából jó eséllyel a jövőben gyakran hivatkozott, magas impaktú folyóiratcikk születik.
A későbbiekben érdekes kutatási irány a módszer vizsgálata fókuszált források szintézisére, amely esetben a visszaállítandó forrás a megfigyelési területen belül helyezkedik el.
Saját publikációk, hivatkozások, linkgyűjtemény
Kapcsolódó saját publikációk listája.
[FG1] G. Firtha and P. Fiala. “Sound Field Synthesis of Uniformly Moving Virtual Monopoles”. In: J. Audio Eng. Soc. 63.1/2 (2015), 46–53. old.
[FG2] G. Firtha and P. Fiala. “Wave Field Synthesis of Moving Sources with Retarded Stationary Phase Approximation”. In: J. Audio Eng. Soc. 63.12 (2016), 958–965. old.
[FG3] G. Firtha and P. Fiala. “Wave Field Synthesis of moving sources with arbitrary trajectory and velocity profile”. In: J. Acoust. Soc. Am. 142.2 (2017), 551–560. old.
[FG4] G. Firtha, P. Fiala, F. Schultz, and S. Spors. “Improved Referencing Schemes for 2.5D Wave Field Synthesis Driving Functions”. In: IEEE/ACM Trans. Audio, Speech, Lang. Process. 25.5 (2017), 1117–1127. old.
[FG5] G. Firtha, P. Fiala, F. Schultz, and S. Spors. “On the General Relation of Wave Field Synthesis and Spectral Division Method for Linear Arrays”. In: IEEE/ACM Trans. Audio, Speech, Lang. Process. (2018) szakmai véleményezésen
[FG6] G. Firtha and P. Fiala. “Spatial Aliasing and Loudspeaker Directivity in Unified Wave Field Synthesis Theory”. In: 44th Annual Conference on Acoustics (DAGA). München, Németország, 2018. március
[FG7] G. Firtha and P. Fiala. “Theory and Implementation of 2.5D WFS of moving sources with arbitrary trajectory”. In: 44th Annual Conference on Acoustics (DAGA). München, Németország, 2018.
[FG8] G. Firtha and P. Fiala. “Investigation of Spatial Aliasing Artifacts of Wave Field Synthesis for the Reproduction of Moving Virtual Point Sources”. In: 42nd German Annual Conference on Acoustics (DAGA). Aachen, Németország, 2016
Linkgyűjtemény:
https://en.wikipedia.org/wiki/Wave_field_synthesis
https://en.wikipedia.org/wiki/Sweet_spot_(acoustics)
https://index.hu/tudomany/2015/03/03/bme_suketszoba_csend_zaj_akusztika/
http://www.iosono-sound.com/company/technology/
http://www.hte.hu/hte-diplomaterv-szakdolgozat-palyazat
https://www.bme.hu/unkp-osztondijasok-2017-18
http://sfstoolbox.org/en/latest/
https://en.wikipedia.org/wiki/Stationary_phase_approximation
https://en.wikipedia.org/wiki/Head-related_transfer_function
Hivatkozások:
[1] A. J. Berkhout, Diemer de Vries and P. Vogel. “Wave Front Synthesis: A New Direction in Electroacoustics”. In: Proc. of the 93rd Audio Eng. Soc. Convention. San Francisco, USA, 1992
[2] A.J. Berkhout, D. de Vries and P. Vogel. “Acoustic Control by wave field synthesis”.
In: J. Acoust. Soc. Am. 93.5 (1993), 2764–2778. old.
[3] E.W. Start. “Direct sound enhancement by wave field synthesis”. PhD tézis. Delft
University of Technology, 1997
[4] E.N.C. Verheijen. “Sound Reproduction by Wave Field Synthesis”. PhD tézis. Delft
University of Technology, 1997
[5] S. Spors, R. Rabenstein and J. Ahrens. “The Theory of Wave Field Synthesis
Revisited”. In: Proc. of the 124th Audio Eng. Soc. Convention. Amsterdam, Hollandia, 2008
[6] J. Ahrens. Analytic Methods of Sound Field Synthesis. 1st. Berlin: Springer, 2012
[7] H. Wierstorf. “Perceptual Assessment of Sound Field Synthesis”. PhD tézis. Tech-
nischen Universitat Berlin, 2014
[8] Winter, F., Ahrens, J. and Spors, S.: “A Geometric Model for Spatial Aliasing in Wave Field Synthesis.” In: 44th German Annual Conference on Acoustics (DAGA). München, Németország, 2018
[9] F. Schultz, G. Firtha, P. Fiala and S. Spors. “Wave Field Synthesis Driving Functions for Large-Scale Sound Reinforcement Using Line Source Arrays”. In: Proc. of the 142nd Audio Eng. Soc. Convention. Berlin, Németország, 2017
[10] W. Zhang, P. N. Samarasinghe, H. Chen, and T. D. Abhayapala. “Surround by Sound: A Review of Spatial Audio Recording and Reproduction”. In: Applied Sciences 7.5
[11] S. Spors and J. Ahrens. “Spatial Sampling Artifacts of Wave Field Synthesis for the Reproduction of Virtual Point Sources”. In: Proc. of the 126nd Audio Eng. Soc. Convention, München, Németország, 2009
[12] V. Erbes, M. Geier, S. Weinzierl and S. Spors. “Database of single-channel and binaural room impulse responses of a 64-channel loudspeaker array”. In: Proc. of the 138th Audio Eng. Soc. Convention. Varsó, Lengyelország, 2015
[13] F. Winter, G. Firtha, J. Ahrens and S. Spors. “Spatial Aliasing in 2.5D Sound Field Synthesis”. In: IEEE/ACM Trans. Audio, Speech, Lang. Process. (2018/2019). beküldés előtt
