George A. Olah Doctoral School of Chemistry and Chemical Technology 

Department of Inorganic and Analytical Chemistry

Supervisor: Dr. Jedlovszky Pál

Molecular Mechanism of Anesthesia

Introducing the research area

In my doctoral research, I studied the structural and dynamical properties of interfaces in molecular simulations. In my work, I describe an efficient method for the calculation of lateral pressure profiles, which has been developed in connection with my investigations of the surface tension, and apply it to study the effect of general anesthetics on living organisms.

 

Brief introduction of the research place

As a doctoral student under shared supervision, I conduct my research at the Department of Inorganic and Analytical Chemistry (BUTE) and at the Université de Bourgogne Franche-Comté. My Hungarian advisor, Dr. Pál Jedlovszky actively contributed in the development of the most popular interfacial analysis methods. He also owns several publications related to the simulation of lipid membranes. Through the extensive international relations of our research group, I have had the opportunity to collaborate with researchers at the University of Vienna and the Czech Academy of Sciences.

 

History and context of the research

On the methods of interfacial analysis:

 

Even though the theoretical bases of the study of fluid interfaces were laid in 1965 [1], it wasn’t until the mid 2000s that a working algorithm was developed to identify the interfacial molecules in computer simulations. This method, named Intrinsic Sampling Method (ISM) [2], represented the surface as a 2D Fourier series. Later, the Identification of the Truly Interfacial Molecules (ITIM) [3] method was developed in our group. The ITIM method is capable of providing data consistent with the results of ISM, but at a fraction of the computational cost. While ITIM could only be applied to macroscopically planar interfaces, its generalized version, the Generalized ITIM (GITIM) [4] is applicable to interfaces of arbitrary shape.

 

On the molecular mechanism of anesthesia:

 

In spite of its widespread application, the molecular mechanism of general anesthetics is still an open question. The general pharmaco-chemical principle of protein-specific interactions seems inapplicable in their case: even the binding locations, where these molecules could act, have remained unknown.

        Alternative explanations are provided by the so called “lipid theories”. According to these, the anesthetics indirectly induce the conformational changes of certain proteins through the perturbation of the membrane structure. In 1997, Cantor proposed the change of the lateral pressure profile of the membrane to be the source of anesthetic action [5]. Experimental investigation of this issue verges on the impossible, as it would entail the determination of the pressure tensor with Angström resolution. Moreover, even the computational approach is non-trivial, since it requires the atomic-scale localization of a quantity, the pressure, that is inherently non-local.

Fig. 1: Changes in the lateral pressure profile induce the conformational changes of certain membrane proteins.

 

        Finally, all possible theories of general anesthesia must account for the experimental phenomenon of pressure-reversal [6], that is, the fact, that elevated ambient pressures diminish or even completely eliminate the effect of general anesthetics.

 

The research goals, open questions

The aim of my work is to investigate the possible mode of action of general anesthetics with the aid of computer simulations. The lipid theories serve as a starting point, since they provide a trivial explanation of the phenomenon of pressure-reversal. The lipid bilayers present in living organisms are highly complex. The various molecular models not only have to adequately represent the behaviour of the lipids: the chemical composition of the membrane is also of great importance, an aspect that should be captured as faithfully as possible.

Furthermore, using non anesthetic molecules closely resembling the structure of general anesthetics can provide additional information on the mechanism of anesthetics. In the current work, the emphasis is placed on the changes in the lateral pressure profile, assessing Cantor’s hypothesis. Based on the conjecture, the relation between the lateral pressure profile and the changes induced in the conformation of proteins is still fairly vague.

 

Methods

Molecular dynamics:

 

Molecular dynamics [7] is a classical mechanical technique for the numerical solution of Newton’s equation of motion. Under suitable initial conditions, and knowing the potential (therefore the acting forces), the system can be propagated forward in time using small, discrete time steps. Such a simulation results in a trajectory that can be further analyzed to obtain dynamical and structural information on the system under study.

 

Interfacial analysis and the ITIM method:

 

The goal of interfacial analysis is to determine the molecules at the surface of their phase. Its physical background is provided in the context of the capillary wave theory. The ITIM method can be applied to macroscopically planar interfaces. In the method, probe spheres are moved along a sufficiently dense set of test lines perpendicular to the surface, starting from the opposite phase. When a probe sphere touches a molecule it stops, and the molecule is considered to be interfacial.

 

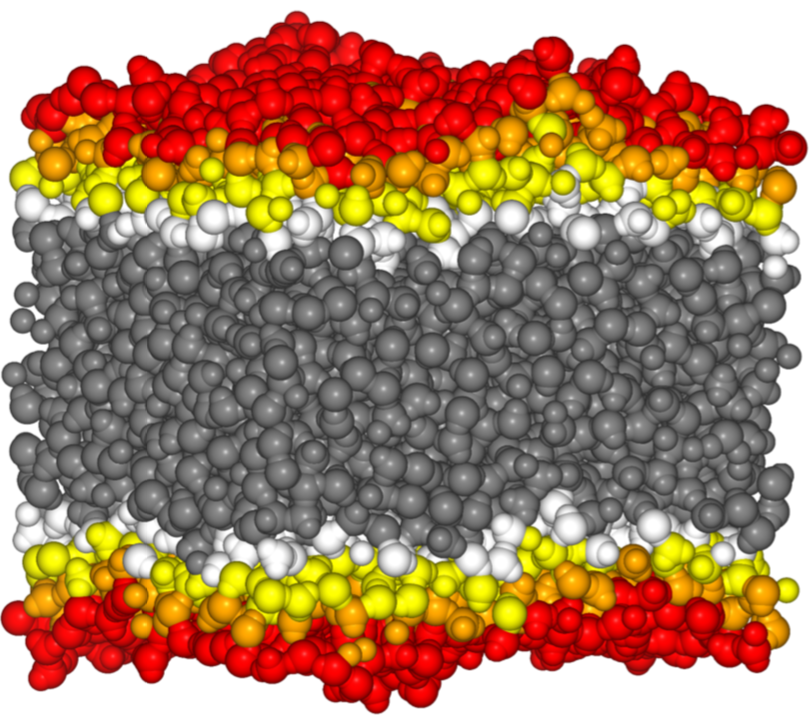
Fig. 2: Interfacial and subsurface layers as determined by the ITIM analysis

 

Results

Pressure profiles and the surface tension:

 

The calculation of pressure profiles requires the molecular scale localization of the pressure. This can be achieved in several ways consistent with the macroscopic results [8]. Here, we use the so-called Harasima contour [9] which enables the distribution of the pressure tensor on the individual atomic sites, thus providing suitable basis for the calculation of pressure profiles. The surface tension can be calculated from the difference of the lateral and normal components of the pressure tensor.

 

Pressure-contribution of the long-range electrostatics:

 

In molecular simulations, the long-range contribution of the Coulomb interaction is handled with the Particle-Mesh Ewald (PME) [10] method. During my interfaces related work, I developed a method that is capable of considering the pressure-contribution of interactions coming from PME quickly and precisely in the course of simulations [S1]. The algorithm provides results consistent with other contours.

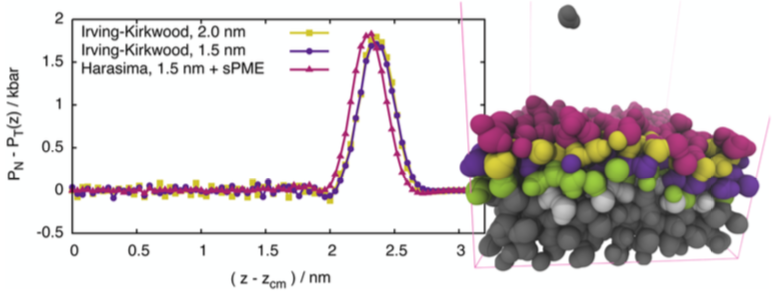
Fig. 3: Pressure profiles calculated using different contours provide comparable results.

 

Surface tension in simple liquids:

 

The proper handling of the long-range electrostatics enables the assignment of the pressure-, therefore the surface tension-contribution to individual atomic sites. Moreover, in combination with the ITIM method, the surface tension can be determined in a layer-wise manner [S2]. In the liquids under study (water, methanol, acetonitrile, acetone and carbon-tetrachloride), the majority of the surface tension is concentrated in the first molecular layer [S3]. While approximately 90% of the surface tension comes from the first layer, nearly 10% originates from the second. From the third layer on, the contribution becomes negligible. This finding is in complete agreement with physical considerations: it is in the vicinity of the interface where the molecules lose a part of their attractive interactions. Surface tension is the energetic cost of this loss.

 

Fig. 4: Surface tension-contribution of the first four molecular layers.

 

Pressure profiles in lipid membranes:

 

Using the method for the calculation of pressure profiles, I investigated the effect of various general anesthetics (diethyl-ether, enflurane, halothane, chloroform) on a DPPC (dipalmitoylphosphatidylcholine) bilayer. I performed the calculation both at 1 and at 1000 bar to take into account the phenomenon of pressure-reversal. The 1000 bar pressure is clearly an exaggeration, but it produces statistically significant changes in the structure of the membrane.

Fig. 5: Structure of a lipid bilayer in the presence of halothane (blue spheres), at 1 and 1000 bar pressure.

 

The anesthetics prefer two distinct positions in the membrane. The first is right in the middle of the bilayer, while the second is in the vicinity of the C=O groups, at the outer edge of the hydrocarbon phase [S4]. According to our results, the molecules around C=O groups induce the lateral expansion of the membrane; therefore, they are most likely to be the responsible for the anesthetic effect [S5]. This finding is in accord with the pressure-reversal: while the anesthetics decrease the lateral pressure around the C=O groups, the increase of external pressure counteracts this effect.

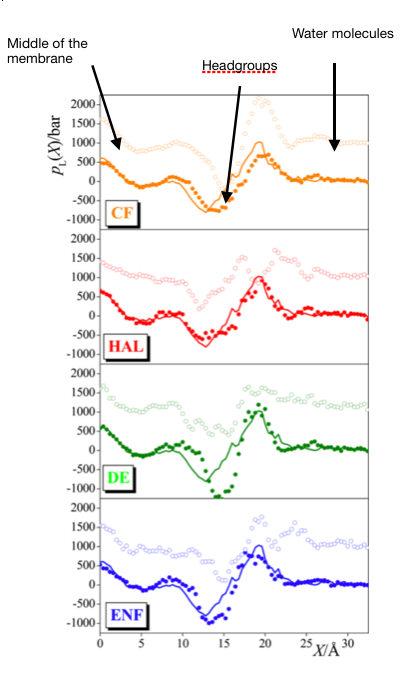
Fig. 6: Lateral pressure profile in various systems. The solid curve represents the pure, 1 bar membrane. The addition of anesthetics shifts the curves to the full circles. Increasing the pressure on these systems results in the empty circles. The systems from the top to the bottom panel: chloroform, halothane, diethyl-ether, enflurane.

 

Expected impact and further research

While in the context of the applied molecular model I have found structural changes of the membrane that can be related to the mechanism of anesthetics, it would be informative to use a more complex membrane composition, which resembles more the conditions encountered in living organisms. Furthermore, simulating non anesthetic molecules that have large structural similarity with certain anesthetics could provide a complementary point of view on the mode of action on these molecules. Such possible pairs are pentane/diethyl-ether, carbon-tetrachloride/chloroform or neon/xenon. Studies in our research group have already started investigating these issues.

 

Publications, references, links

List of corresponding own publications:

[S1] M. Sega, B. Fábián and P. Jedlovszky, J. Chem. Theo. Comput., 2016, 12, 4509

[S2] M. Sega, B. Fábián and P. Jedlovszky, J. Chem. Phys, 2015, 143, 114709

[S3] M. Sega, B. Fábián, G. Horvai and P. Jedlovszky, 2015, 120, 48, 27468

[S4] B. Fábián, M. Darvas, S. Picaud, M. Sega and P. Jedlovszky, Phys. Chem. Chem. Phys., 2015, 17, 14750

[S5] B. Fábián, M. Sega, V. P. Voloshin, N. N. Medvedev and P. Jedlovszky, J. Chem. Phys. B, 2017, 121, 2814

 

List of references:.

[1] F. P. Buff, R. A. Lovett and F. H. Stillinger, Phys. Rev. Lett., 1965, 15, 621

[2] P. Tarazona and E. Chacón, Phys. Rev. B, 2004, 70, 235407

[3] L. B. Pártay, G. Hantak, P. Jedlovszky, A. Vincze and G. Horvai, J. Comput. Chem., 2007, 29, 945

[4] M. Sega, S. S. Kantorovich, P. Jedlovszky and M. Jorge, J. Chem. Phys., 2013, 138, 044110

[5] R. S. Cantor, Biochemistry, 1997, 36, 2339

[6] F. H. Johnson and E. A. Flagler, Science, 1950, 112, 91

[7] B. J. Alder and T. Wainwrigth, J. Chem. Phys., 1957, 27, 1208

[8] J. M. Vanegas, M. L. Longo and R. Faller, J. Am. Chem. Soc., 2011, 133, 3720

[9] A. Harasima, Adv, Chem. Phys., 1958, 1, 203

[10] U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577