Oláh György Doktori Iskola 

Szervetlen és Analitikai Kémiai Tanszék

Témavezető: Dr. Jedlovszky Pál

Anesztetikumok molekuláris hatásmechanizmusa

A kutatási téma néhány soros bemutatása

Doktori munkám során határfelületek szerkezeti és dinamikai sajátságait tanulmányoztam molekuláris szimulációkban. Kutatásom első felében egyszerű molekuláris folyadékok határfelületi tulajdonságait vizsgáltam. Pályázatomban bemutatok egy, a felületi feszültséggel kapcsolatos kutatásaim során kifejlesztett gyors és pontos nyomásprofil-számoló eljárást, majd ennek segítségével vizsgálom általános anesztetikumok hatását az élő szervezetekre.

A kutatóhely rövid bemutatása

Kutatásaimat a BME Szervetlen és Analitikai Kémia Tanszékén és az Université de Bourgogne Franche-Comté-n végzem, kettős témavezetéssel. Magyar témavezetőm, Dr. Jedlovszky Pál aktívan közreműködött a legnépszerűbb felületmeghatározó módszerek kifejlesztésében, emellett a lipidmembránok területen is számos publikációval rendelkezik. Csoportunk nemzetközi kapcsolatai révén alkalmam nyílt együttműködni többek között a Bécsi Egyetemmel és a Cseh Tudományos Akadémiával is.

A kutatás történetének, tágabb kontextusának bemutatása

A határfelületekről:

 

A fluid fázisok határfelülete tanulmányozásának elméleti alapjait 1965-ben fektették le [1], azonban egészen a 2000-es évek elejéig várni kellett az első olyan eljárásra, amely képes volt a határfelületi molekulák azonosítására számítógépes szimulációkban. Ez az Intrinsic Sampling Method (ISM) [2] volt, ami a felületet kétdimenziós Fourier-sorral definiálta, amely egy önkonzisztens feltétellel meghatározható. Kutatócsoportunkban ezután került kidolgozásra az Identification of the Truly Interfacial Molecules (ITIM) [3] módszer, amely az ISM-mel összeegyeztethető eredményeket nyújt a számítási költségek töredékéért. Míg az ITIM csak makroszkopikusan sík felületek esetében működik, addig általánosítása, a Generalized ITIM(GITIM) [4], már tetszőleges geometriákra alkalmazható.

 

Az általános anesztetikumok hatásmechanizmusáról:

 

Annak ellenére, hogy napjainkban széles körben alkalmazzák őket, az általános anesztetikumok molekuláris hatásmechanizmusa a mai napig nem tisztázott. A gyógyszerek fehérjespecifikus működésének elve esetükben nehezen alkalmazható, és még ma sem ismert a fehérjék olyan aktív helye, ahol kifejthetnék hatásukat.

        Alternatív magyarázatot nyújtanak az úgynevezett “lipidelméletek”, amelyek szerint az anesztetikumok a lipidmembránok szerkezetének megváltoztatásával, közvetett módon idézik elő bizonyos fehérjék konformációjának változást. Cantor 1997-ben tett javaslata [5] szerint a lipidkettősréteg laterális nyomásprofiljának megváltozása lehet az anesztetikus hatás kulcsa. Elméletének kísérleti vizsgálata lehetetlennek tűnik, mivel a nyomástenzor Angström felbontású meghatározását igényli. Mindemellett számítógépes vizsgálata sem triviális, mert egy alapvetően nem-lokális mennyiség, a nyomás atomi szintű lokalizálását igényli.

 

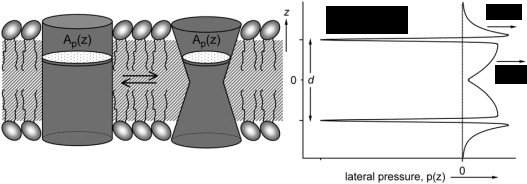
1. ábra: A nyomásprofil megváltozása a membránbeli fehérjék konformációs megváltozását okozhatja.

 

        Végezetül, bármely felmerülő elméletnek meg kell magyaráznia a nyomásreverzió jelenségét, amely szerint megnövelt nyomáson megszűnik az anesztetikus hatás [6].

 

A kutatás célja, a megválaszolandó kérdések

Kutatásaim célja az általános anesztetikumok hatásmechanizmusának feltérképezése számítógépes szimulációkkal. A lipidelméletek kiindulási pontként szolgálnak, mivel segítségükkel triviálisan magyarázható a kísérletekben megfigyelt nyomásreverzió jelensége. A szervezetben megtalálható lipidkettősrétegek rendkívül összetettek, a felállított modellnek minél valóságosabban kell reprezentálnia a bennük megtalálható sokféle vegyületet. Nemcsak az a fontos, hogyan hat az általános anesztetikum jelenléte a membrán tulajdonságaira, hanem az is, hogy a különböző membránmodellek és összetételek mennyire hűen ragadják meg a modellezni kívánt valós rendszer sajátságait.

Emellett összehasonlítási alapul szolgálhatnak olyan rendszerek, amelyekben az anesztetikumok szerkezetéhez hasonló, de anesztetikus hatást nem mutató molekulák által előidézett változások vizsgálhatók. Jelen kutatásaimban nagy hangsúlyt fektetek a laterális nyomásprofilok megváltozására, azaz a Cantor-féle hipotézis értékelésére. Az elmélet alapján azonban még mindig nyitott kérdés, hogyan is történik meg a fehérje-konformáció változása a nyomásprofilok megváltozása miatt.

Módszerek

Molekuláris dinamika:

 

A molekuláris dinamika [7] egy klasszikus mechanikára, azon belül a newtoni mozgásegyenletek numerikus megoldására épülő módszer. Lényege, hogy az atomok közötti potenciál, és így a köztük ható erő ismeretében, megfelelő kezdeti feltételek mellett, kis időlépésekben propagáltatjuk a rendszert. Az eredmény egy pillanatfelvételekből álló trajektória, amelyen további elemzéseket végezhetünk.

 

Felületelemzés és az ITIM módszer:

 

Az elemzés célja a határfelületi molekulák meghatározása. Fizikai alapját a kapillárishullám-elmélet szolgáltatja. Az ITIM makroszkopikusan sík felületek esetén alkalmazható. A módszer során próbagolyót mozgatunk a felületre merőleges, sűrű tesztvonalak mentén, az ellenkező fázisból kiindulva. Amint a golyó érintkezik egy molekulával, megáll, és az eljárás a molekulát határfelületinek jelöli meg.

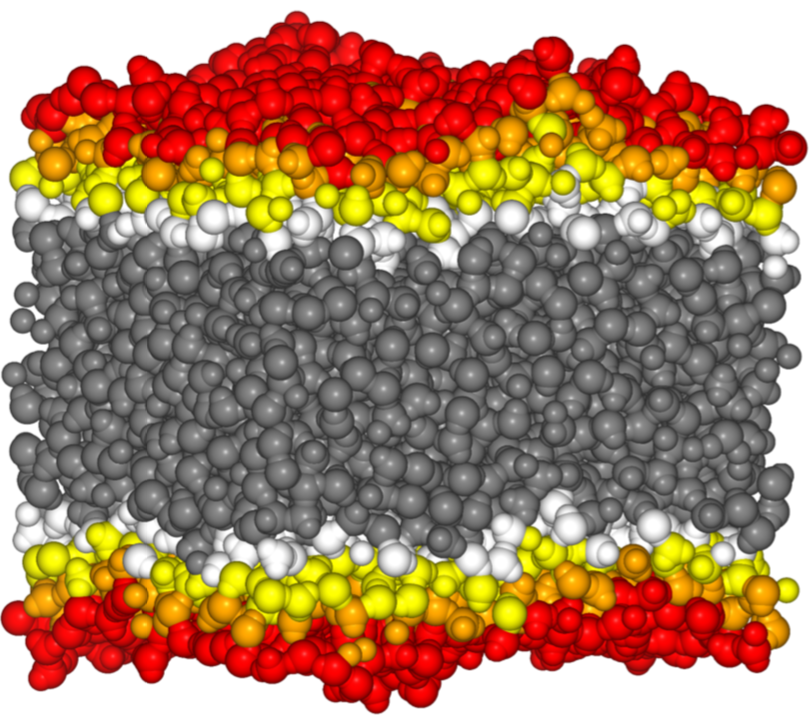
2. ábra: Az ITIM felületelemző által meghatározott felületi, és felület alatt húzódó rétegek

Eddigi eredmények

Nyomásprofilok és a felületi feszültség:

 

A nyomásprofilok számítása megkívánja a nyomás molekuláris szintű lokalizálását. Ezt többféleképpen el lehet végezni úgy, hogy hasonló makroszkopikus eredményeket nyújtson [8]. Az általunk használt Harasima kontúr [9] lehetővé teszi a nyomásjárulék hozzárendelését az egyes atomokhoz, így megfelelő alapot nyújt a profilok számításához. A felületi feszültséget a nyomásprofil laterális és normális értékeinek különbségéből származtathatjuk.

 

A hosszútávú elektrosztatika nyomásjáruléka:

 

A töltött részecskék között fellépő Coulomb-erők hosszútávú részét a Particle-Mesh Ewald (PME) [10] módszerrel számolják. Határfelületekkel kapcsolatos munkám során kidolgoztam egy eljárást, amellyel a PME-ből származó erők nyomásjáruléka gyorsan és nagy pontossággal figyelembe vehető a szimulációk során [S1]. A módszer más kontúrokkal összevetve is kielégítő eredményeket ad.

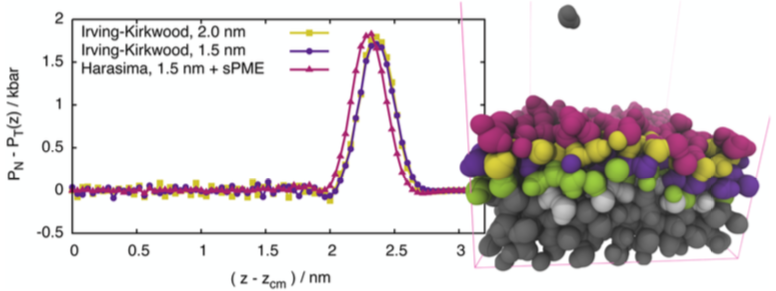
3. ábra: A különböző kontúrokkal számolt nyomásprofilok hasonló eredményeket adnak

 

Felületi feszültség egyszerű folyadékokban:

 

A hosszútávú elektrosztatika korrekt kezelése lehetővé teszi a nyomás-, így a felületifeszültség-járulék atomokhoz való hozzárendelését. Mi több, az ITIM módszerrel kombinálva kiszámítható az egyes molekuláris rétegek felületifeszültség-hozzájárulása is [S2]. Az általunk vizsgált egyszerű folyadékok (víz, metanol, acetonitril, aceton, szén-tetraklorid) felületi feszültsége nagymértékben az első molekuláris rétegben koncentrálódik [S3]. A felületi feszültség legalább 90%-a innen származik, míg 10% a második rétegből. A harmadik rétegtől kezdve a felületi feszültség elhanyagolható. Ezek az eredmények teljesen összhangban vannak a fizikai képpel, miszerint a felületi feszültség a felszín közelében lévő molekulák által érzett aszimmetrikus erőkből származik: ezek a molekulák elvesztik vonzó kölcsönhatásaik egy részét, ennek az energetikai költsége a felületi feszültség.

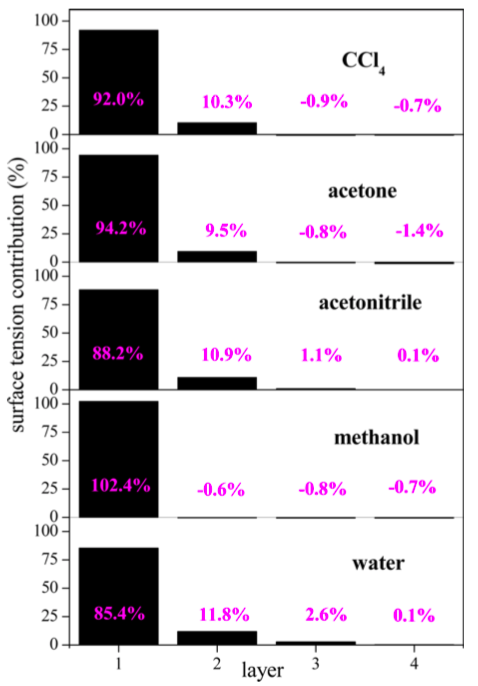
4. ábra: Az egyes folyadékok első négy felületi rétegének járulékai a felületi feszültséghez

 

Nyomásprofil lipidmembránokban:

A kidolgozott nyomásprofil-számoló segítségével különböző anesztetikum molekulák (dietil-éter, enflurán, halotán, kloroform) hatását tanulmányoztam DPPC (dipalmitoilfoszfatidilkolin) lipidkettősrétegek nyomásprofiljaira. A számításokat 1 és 1000 bar nyomáson is elvégeztem, ezzel figyelembe véve a megnövekedett nyomás hatását, a nyomásreverzió jelenségét. Az 1000 bar nyomás bár fiziológiailag irreális, számítógépes szimulációkban egyszerűen kivitelezhető, és a megnövelt nyomáskülönbség statisztikailag könnyebben észlelhető eltéréseket eredményez profilokban.

5. ábra: A lipidkettősréteg szerkezete halotán anesztetikum jelenlétében (kék gömbök) 1 és 1000 bar nyomáson

 

Az anesztetikumok a membrán két különböző részén, a kettősréteg közepén és a C=O csoportok környékén, szénláncok végénél dúsulnak fel [S4]. Eredményeink alapján a C=O csoportok körüli molekulák váltják ki a membrán laterális expanzióját, így valószínűleg ők felelősek az anesztetikus hatás kialakításáért [S5]. A talált összefüggés a nyomásreverzió jelenségét is megmagyarázza: míg az anesztetikumok lecsökkentik a C=O csoportok körüli nyomást, addig a megnövelt külső nyomás az ellenkező irányba hat, növelve azt.

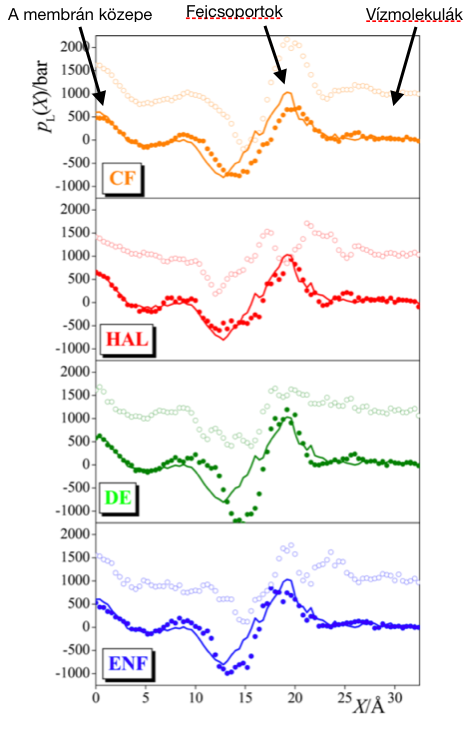
6. ábra: Laterális nyomásprofil a különböző membránokban. A folytonos görbe az anesztetikumtól mentes rendszer, amely az anesztetikumok hozzáadására a teli színes körökbe megy át. A nyomást ekkor megnövelve kapjuk az üres színes köröket. Az adatsorok fentről lefelé: kloroform, halotán, dietil-éter, enflurán

 

Várható impakt, további kutatás

Habár a vizsgált modellrendszer keretében sikerült olyan, a lipidkettősréteg szerkezeti változásával kapcsolatos összefüggéseket találnunk, amelyek magyarázhatják az általános anesztetikumok hatásmechanizmusát, célszerű lenne olyan számítások elvégzése, ahol a membrán összetétele komplexebb, így nagyobb hasonlóságot mutat az élő szervezetekben is megtalálhatókhoz. Hasznos lehet továbbá olyan, anesztetikus hatást nem mutató molekulák tanulmányozása, amelyek szerkezetileg hasonlítanak bizonyos általános anesztetikumokhoz. Ilyen párok például pentán és dietil-éter, szén-tetraklorid és kloroform, neon és xenon. Kutatócsoportunkban már jelenleg is folynak az ezzel kapcsolatos vizsgálatok.

 

Saját publikációk, hivatkozások, linkgyűjtemény

Kapcsolódó saját publikációk listája.

[S1] M. Sega, B. Fábián and P. Jedlovszky, J. Chem. Theo. Comput., 2016, 12, 4509

[S2] M. Sega, B. Fábián and P. Jedlovszky, J. Chem. Phys, 2015, 143, 114709

[S3] M. Sega, B. Fábián, G. Horvai and P. Jedlovszky, 2015, 120, 48, 27468

[S4] B. Fábián, M. Darvas, S. Picaud, M. Sega and P. Jedlovszky, Phys. Chem. Chem. Phys., 2015, 17, 14750

[S5] B. Fábián, M. Sega, V. P. Voloshin, N. N. Medvedev and P. Jedlovszky, J. Chem. Phys. B, 2017, 121, 2814

 

Hivatkozások listája.

[1] F. P. Buff, R. A. Lovett and F. H. Stillinger, Phys. Rev. Lett., 1965, 15, 621

[2] P. Tarazona and E. Chacón, Phys. Rev. B, 2004, 70, 235407

[3] L. B. Pártay, G. Hantak, P. Jedlovszky, A. Vincze and G. Horvai, J. Comput. Chem., 2007, 29, 945

[4] M. Sega, S. S. Kantorovich, P. Jedlovszky and M. Jorge, J. Chem. Phys., 2013, 138, 044110

[5] R. S. Cantor, Biochemistry, 1997, 36, 2339

[6] F. H. Johnson and E. A. Flagler, Science, 1950, 112, 91

[7] B. J. Alder and T. Wainwrigth, J. Chem. Phys., 1957, 27, 1208

[8] J. M. Vanegas, M. L. Longo and R. Faller, J. Am. Chem. Soc., 2011, 133, 3720

[9] A. Harasima, Adv, Chem. Phys., 1958, 1, 203

[10] U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577