Géza Pattantyús-Ábrahám Doctoral School of Mechanical Engineering Sciences 

Department of Applied Mechanics

Supervisor: Dr. Kossa Attila

Viscous-elastic-plastic modelling of polymeric foam materials

Introducing the research area

Today’s state-of-art materials (especially polymers and composites) might show extremely complex mechanical behaviour during their industrial and everyday application that can be characterized by not only elastic but also viscous and/or permanent deformations [R1]. However, the number of available constitutive equations, that describe such phenomena with adequate accuracy, is highly limited. The goal and the motivation of my research is to investigate the viscous-elastic-plastic material behaviour and models using both analytical and experimental methods through the study of polymer foams in order to develop the available models and increase the accuracy of finite element simulations.

Brief introduction of the research place

The place of my research is the Department of Applied Mechanics at the Faculty of Mechanical Engineering. The Department with more than 150 years of history focuses on rigid body dynamics (including machine tool vibrations, human balancing and tyre dynamics), but the researches in the field of continuum mechanics are also significant. Our former researcher, Endre Reuss is linked, for example, to the so-called Prandtl-Reuss equations, one of the basic theories in plasticity.

History and context of the research

The recent digital revolution has enabled us to investigate engineering tasks quickly with finite element simulations and to support the process design and the optimization of manufacturing processes. Commercially available finite element software (e.g. Abaqus, Ansys, MSC Marc) offer several material models and their proper choice is essential for the accurate modelling of the investigated phenomena [R1,R2].

Simultaneously, polymer technology has also undergone enormous development, which has resulted in the appearance of new materials. These materials are characterized by deformations accompanied by large strains and displacements and may show nonlinear, viscous and permanent deformations.

In the literature, the phenomenological approach is a widely adopted method for the modelling of complex mechanical behaviour. Accordingly, the constitutive equation is fitted to measurement results carried out on a couple of load cases. Note that these models can provide accurate results only for loading cases that was applied during the calibration. Also, a generally accepted single model does not exist and the adequacy of a chosen model for describing the true behaviors depends on the properties of the currently investigated material. [R1].

Polymer foams (Figure 1.) are widely applied materials thanks to their favorable mechanical behaviour and excellent energy absorption properties. These foams are applied mostly in the field of impact protection, but they also found their applications among everyday products, like mattresses or earplugs. Due to the wide range of utilization, producing polymer foams is currently an active development direction in polymer technology, which underlines the significance of mechanical modelling [R3].

 

 

Figure 1: Polymer foams in our everyday life: a) Polifoam mattress b) earplug c) impact-proof box d) memory foam mattress

(Source of images: matracom.hu; fortempack.hu és regiojatek.hu)

 

The research goals, open questions

The goal of this research is to investigate the mechanical models and parameter fitting approaches applied for polymer foams. From the industrial point of view, one of the most important questions is to determine the effect of the skin layer (created during the manufacturing process) on the overall behaviour of the foam assuming pure elastic behaviour. Also, the significance of this effect in both machining direction and perpendicularly should also be evaluated.

A further mechanical property characteristic of foams is the time-dependent so-called viscoelastic behaviour characterized by creep and stress relaxation. Such time-dependent foams (commonly also known as memory foams) are applied in bed mattresses and earplugs. Unfortunately, a closed-form stress solution for such material models is not available, which makes fitting of material parameters difficult. My goal is to determine the closed-form stress solution for both open- and closed-cell polymer foams and to improve the parameter fitting procedure [R4,R5,R6].

Additionally, I also study a special branch of foams, namely the microcellular polymer foams (Figure 2.). In industry, the most widely applied manufacturing process of microcellular polymer foams is thermoforming. To model this manufacturing process accurately, the material model is expected to describe the material behaviour adequately at various process temperatures. This research also aims to investigate the applicability of material models used various commercially available finite element software and to develop a parameter fitting algorithm to determine the temperature-dependent material parameters.

 

 

Figure 2: The microscope images of the investigated foam materials

 

Methods

During my research, I studied the various approaches to model polymer foams using both analytical and numerical methods. The applicability of the proposed results and algorithms in practice were validated through mechanical measurements. The scope of tests included open- and closed-cell foams, memory foams and microcellular foams.

Visco-hyperelastic modelling

The deformation of polymer foams shows large displacements and nonlinear stress-strain characteristics. To describe this purely elastic material behaviour, so-called hyperelastic material models should be implemented. Due to the high volumetric compression of foams, the compressible hyperelastic model by Ogden-Hill was applied as most widely known from literature. [R4,R5]. On the other hand, the viscoelastic behaviour was modelled using a visco-hyperelastic model, which combines the large strain generalized Maxwell model and Ogden-Hill’s model (Figure 3). This constitutive equation connects the Kirchhoff stress tensor and the principle stresses in the form of a convolution integral. The model defines the time-dependent moduli using Prony-series, where the order of the Prony-series indicates the number of parallel branches in the Maxwell-model [R2].

 

 

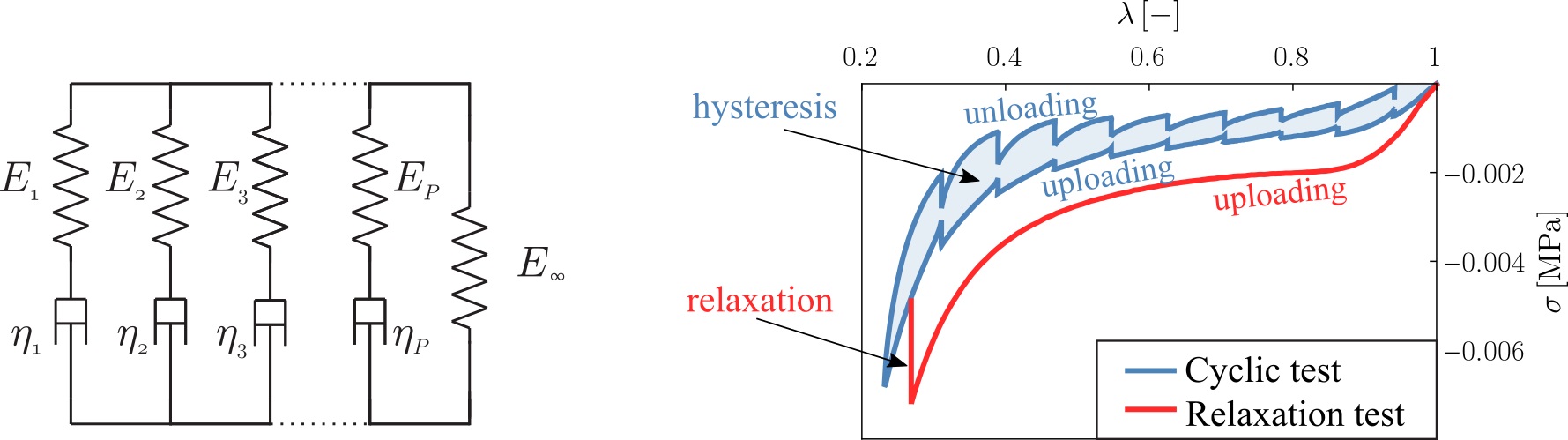
Figure 3: The generalized Maxwell-model applied for memory foams and the captured viscoelastic behaviour during the mechanical tests

 

A possible method to fit the visco-hyperelastic material model is to separate the determination of the pure hyperelastic parameters from the time-dependent Prony-ones. This method, however, introduces significant error in the parameter-fitting process being based on the assumption of an ideal relaxation test [R6]. Based on the analytical solution of the convolution integral for a relaxation test with finite uploading time, a closed form solution can be derived. Using this solution, all the material parameters can be fitted to the measurement data in a single step. The performance of this closed-form method was validated on cyclic and relaxation tests carried out on particular polyethylene memory foam.

Viscous-elastic-plastic modelling

During the thermoforming of microcellular polymer foams, the permanent deformation becomes significant in addition to the elastic and viscous behaviour. Therefore, another constitutive model should be selected for the mechanical modelling. Firstly, I performed cyclic mechanical tests on a microcellular polyethylene-terephthalate (MC-PET) material at different temperatures. For the characterization of such mechanical behaviour the “two-layer viscoplastic” model was applied, which is available in Abaqus [R2, R7]. This model comprises of an elastic-plastic model in parallel with a viscoelastic branch containing altogether 8 material parameters (Figure 4.). Since the closed-form stress-solution cannot be derived, an inverse parameter-fitting method should be developed [R8].

 

 

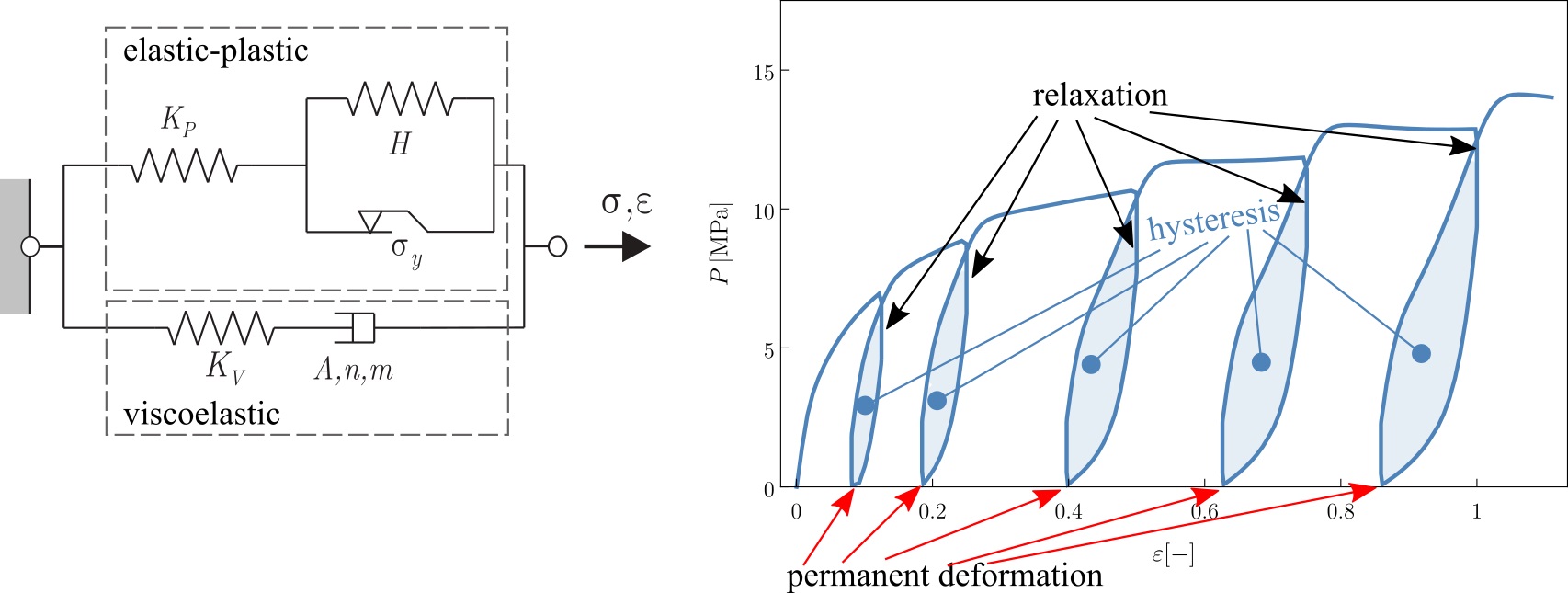
Figure 4: Schematics of the “two-layer viscoplastic” model applied for modelling of thermoforming and the captured viscous-elastic-plastic behaviour based on cyclic mechanical tests.

 

Results

Nonlinear modelling of open- and closed-cell foams

At the beginning of my research, I investigated open- and closed-cell foams using the finite strain Ogden-Hill’s hyperelastic model. Based on uniaxial and biaxial mechanical tests, the effect of the surface skin layer and the machining directions were demonstrated (Figure 5.). Additionally, by proposing a new optimization criterion, the pure hyperelastic parameter-fitting procedure was improved and the hyperelastic parameters were fitted [B1, B2].

 

 

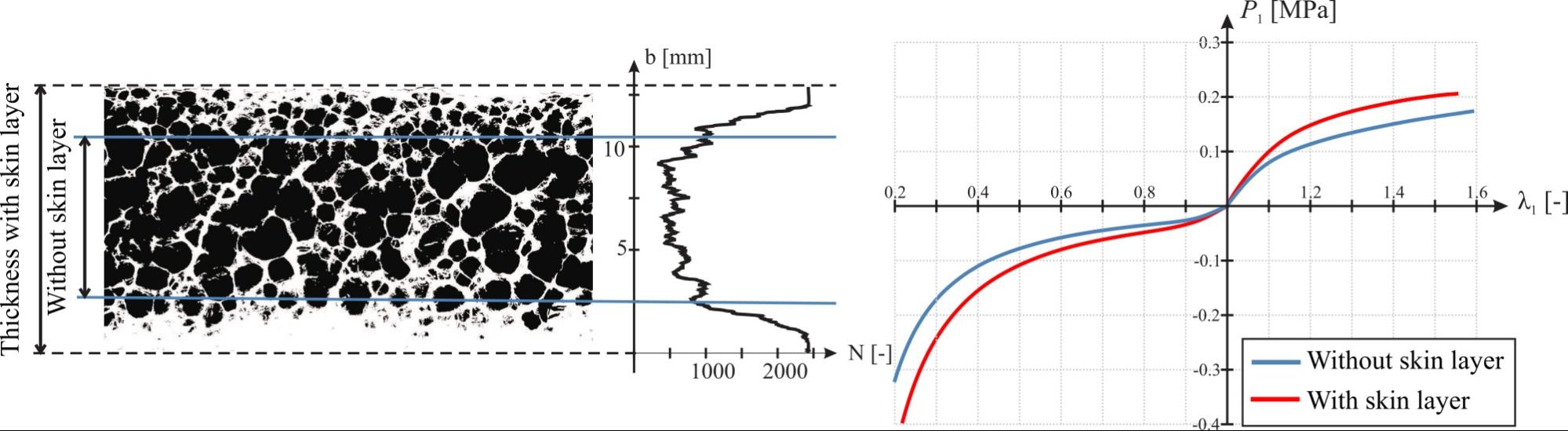
Figure 5: The detected surface skin layer on the microscope image and the effect of the skin layer on the stress-strain characteristics

 

Modelling of time-dependent memory foams

The finite strain viscous-elastic behaviour of memory foams were investigated using the visco-hyperelastic constitutive equation in Abaqus. Based on the case study of open-cell memory foams, a closed-form stress solution was derived for the visco-hyperelastic model based on the Ogden-Hill’s model in case of uniaxial loading.

Subsequently, the closed-form solution was generalized for closed-cell foams and further loading cases (biaxial, volumetric compression). I also proved that using the closed-form stress solution improved the accuracy of the parameter fitting procedure compared to the approximation methods available in literature (Figure 6.). The methods of the fitting methods were compared using the finite element simulation of sitting on the memory foam [B3, B5, B8, B11, B13].

 

 

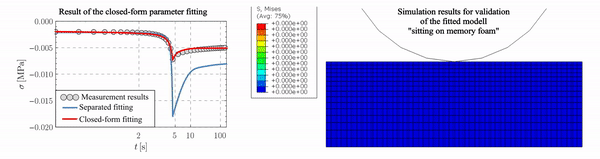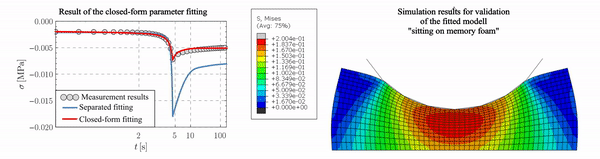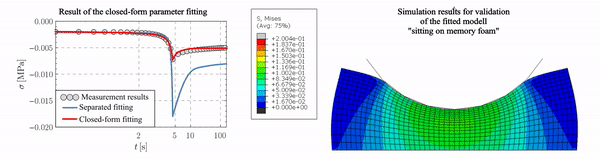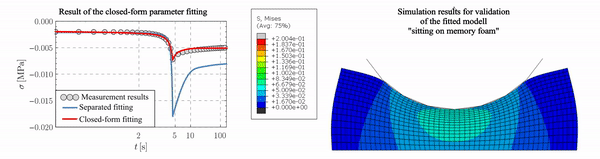
Figure 6: The results of the parameter fitting using the closed-form solution and the finite element simulation applied for validation

 

Modelling of the thermoforming of microcellular foams

Based on uniaxial tensile tests (cyclic and relaxation), I demonstrated that the mechanical behaviour of the investigated microcellular (MC-PET) polymer foam shows viscous-elastic-plastic behaviour. I also found that the “two-layer viscoplastic” model, which is available in the commercial finite element software, characterize this behaviour with good accuracy. However, at elevated temperatures the models became less accurate due to the increase of viscous effects (Figure 7.) [B6, B12].

Since a closed-form solution is not available, a new finite-element-based optimization method was proposed for the parameter-fitting. This method performs the complete finite element simulation of the problem in each iteration step [B4,B7].

 

 

 

 

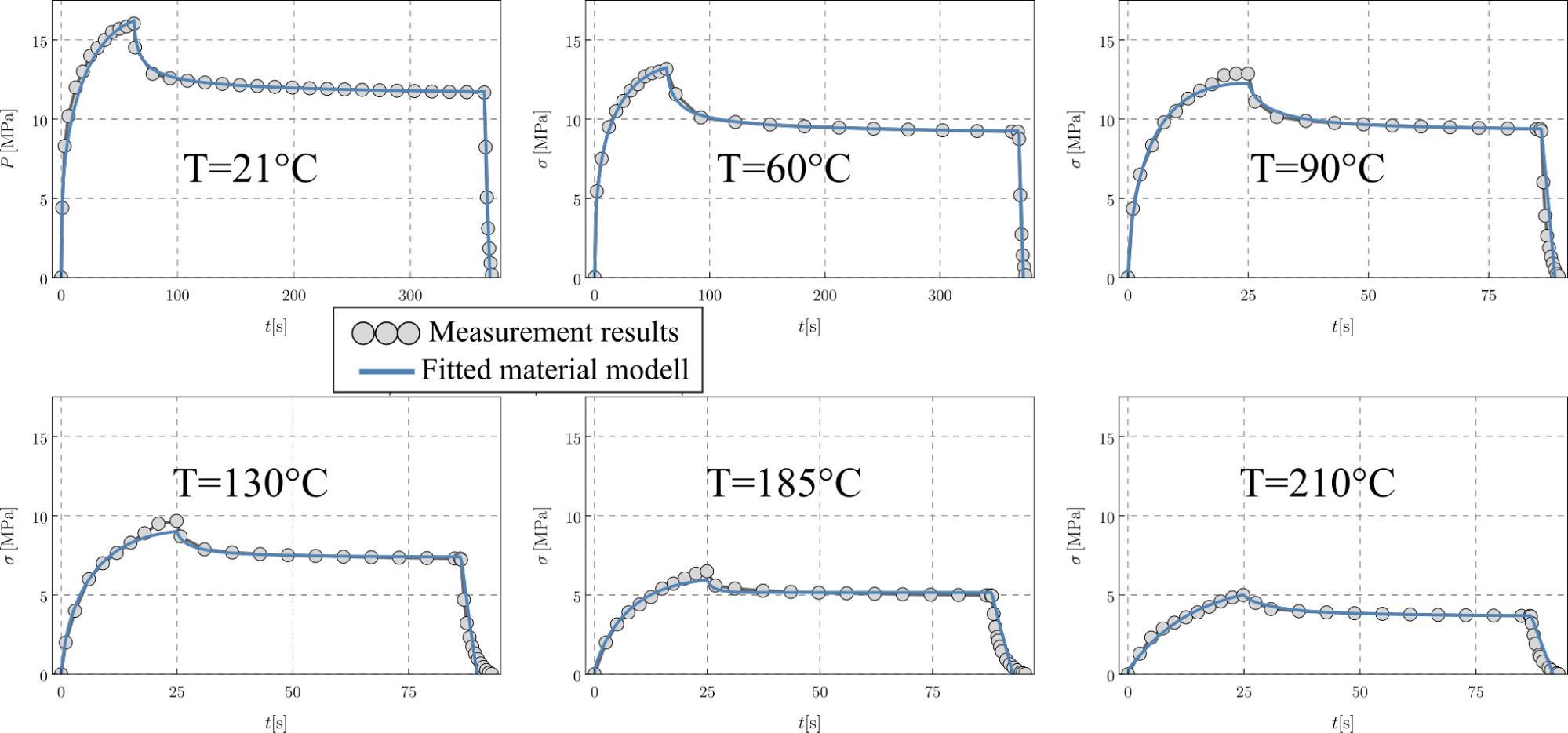
Figure 7: The performance of the fitted material model at different temperature levels applied for characterizing the thermoforming process

 

The equivalent models of the “two-layer viscoplastic” model for dynamical simulations

During the investigation of the “two-layer viscoplastic model” I concluded that this model does not support dynamical simulations. The reason is that the viscous model is not implemented for explicit solver in Abaqus. As a solution, I developed two equivalent elastic-plastic models assuming instantaneous and long-term deformations, respectively. These models can provide lower and upper estimations of the investigated dynamical phenomena. For the validation of this proposed method, the impact of porous airsoft pellets were studied because the impact of the pellet showed viscous-elastic-plastic behaviour can be adequately modelled with the “two-layer viscoplastic” model (Figure 8.) [B4, B7].

 

 

 

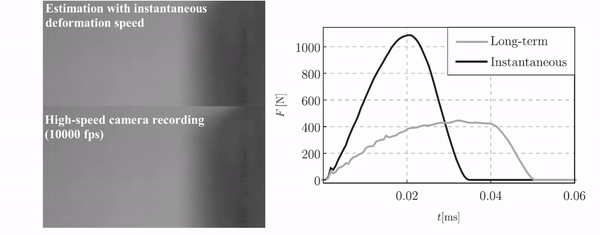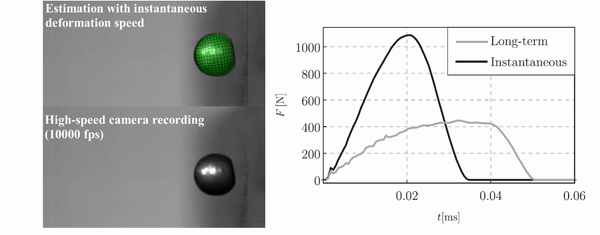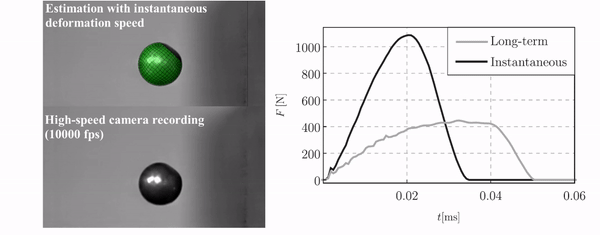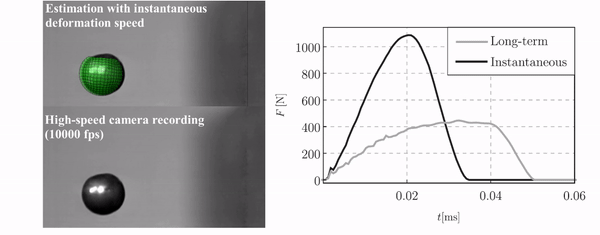
Figure 8: The comparison of the high-speed camera recordings with the finite element simulation and the contact force characteristics in case of airsoft pellet impacts.

 

Expected impact and further research

Thanks to the results of the research, we could obtain a comprehensive picture of the mechanical behaviour of polymer foams (including open- and closed cell foams, memory foams and microcellular foams) and the corresponding material models. The results enable the industry to more accurately simulate manufacturing and application processes. This might also help in the calibration of technological parameters, thus accelerating the manufacturing process.

Regarding the future plans, I would like to focus on the mechanical modelling of thermoforming. In addition to the models implemented in the finite element software, a number of parallel models are available (e.g. Bergström – PolyUMod library), that might be suitable for the modelling of the complex phenomena of thermoforming. In the future, I plan to examine these models for their applicability and use the experiences learned to develop a new material model.

Publications, references, links

List of corresponding own publications.

[B1] Berezvai Sz., Kossa A. Effect of the skin layer on the overall behavior of closed-cell polymer foams, Journal of Cellular Plastics, 52: 215-229 (2016) (IF=1,979)

[B2] Kossa A., Berezvai Sz. Novel strategy for the hyperelastic parameter fitting procedure of polymer foam materials, Polymer Testing, 53: 149-155 (2016) (IF=2,464)

[B3] Berezvai Sz., Kossa A. Closed-form solution of the Ogden-Hill's compressible hyperelastic model for ramp loading, Mechanics of Time-Dependent Materials, 21: 263-286 (2017) (IF=1,014)

[B4] Berezvai Sz., Kossa A. Bachrathy D., Stépán G. Numerical and experimental investigation of the applicability of pellet impacts for impulse excitation, Impact Engineering 2018, vol. 115: 19-31.(IF=2,938)

[B5] Kossa A., Berezvai Sz. Visco-hyperelastic characterization of polymeric foam materials, Materials Today: Proceedings 3: 1003-1008 (2016)

 

[B6] Berezvai Sz., Kossa A. Characterization of a thermoplastic foam material with the two-layer viscoplastic model, Materials Today: Proceedings 4: 5749-5754 (2017)

[B7] Berezvai Sz., Kossa A., Stépán G. Airsoft lövedék viszkózus-rugalmas-képlékeny ütközésének szimulációja és alkalmazása, XXVI. Nemzetközi Gépészeti Találkozó (OGÉT 2016), Tirgu Mures, Romania, April 26-29, 2018. pp. 39-42,

[B8] Berezvai Sz., Kossa A. Memóriahabok mechanikai modellezése, XXIV. Nemzetközi Gépészeti Találkozó (OGÉT 2016), Deva, Romania, April 21-24, 2016,. pp. 47-50,

[B9] Berezvai Sz., Kossa A., Stépán G. Nonlinear material modelling of an airsoft pellet applied for impulse excitation, 9th European Nonlinear Dynamics Conference (ENOC). 2017, Budapest, Hungary,

[B10] Berezvai Sz., Kossa A., Stépán G. Investigation of the performance of the two-layer viscoplastic model applied for simulating airsoft ball impacts, XIV International Conference on Computational Plasticity, 2017, Barcelona, Spain,

[B11] Berezvai Sz., Kossa A. Nonlinear viscoelastic characterization of polymer foams, European Congress on Computational Methods in Applied Sciences and Engineering (ECCOMAS), 2016, Crete, Greece,

[B12] Kossa A., Berezvai Sz. Characterization of a thermoplastic foam material with the two-layer viscoplastic model, 33rd International Danubia-Adria Symposium on Advances in Experimental Mechanics, 2016, Portoroz, Slovenia,

[B13] Kossa A., Berezvai Sz. Visco-hyperelastic characterization of polymer foam materials, 32nd International Danubia-Adria Symposium on Advances in Experimental Mechanics, 2015, Starý Smokovec, Slovakia

 

Table of links.

Material library of Bergström: https://polyumod.com/

Abaqus finite element software: www.simulia.com/

Memoryfoams: https://hu.wikipedia.org/wiki/Memóriahab

Microcellular foams: https://en.wikipedia.org/wiki/Microcellular_plastic

 

List of references.

[R1] J. Bergström. Mechanics of Solid Polymers, 2015, Elsevier.

[R2] ABAQUS 2018 Documentation. Dassault Systems, Simulia Corporation, Providence, Rhode Island, USA.

[R3] LJ. Gibson and MF. Ashby Cellular Solids, 2nd edition, Cambridge University Press,

1997.

[R4] R. W. Ogden. Large deformation isotropic elasticity: On the correlation of theory and experiment for compressible rubberlike solids, Proceedings of the Royal Society of London, Series A, Mathematical and Physical Sciences, 328:567-583, 1972.

[R5] R. Hill. Aspects of invariance in solid mechanics, Advances in Applied Mechanics, 18:1-78, 1978.

[R6] W.G. Knauss, I. Emri, H. Lu. Mechanics of Polymers: Viscoelasticity. In: W.N. Sharpe, Springer Handbook of Experimental Solid Mechanics, 2008, Springer.

[R7] J. Kichenin. Comportement Thermomécanique du Polyéthylène – application aux structures gazieres. PhD thesis. Ecole Polytechnique, Paris, France, 1992.

[R8] ISIGHT 5.9-2. Dassault Systems, Simulia Corporation, Providence, Rhode Island, USA.