Géza Pattantyús-Ábrahám Doctoral School of Mechanical Engineering 

BME GPK, Department of Energy Engineering

Supervisor:  Dr. Sztankó Krisztián

Characterization of Spray Generated by Air Blast Atomizer

Introducing the research area

The aim of my doctoral research is to characterize the spray generated by air blast atomizer using advanced measurement devices. Characterization of the spray and analytical and numerical modeling of the atomization process can open the door to more efficient use of liquid fuels, with special emphasis on high viscosity vegetable oils (rape, sunflower oil). For illustrative purpose, the type of used atomizer is shown in Figure 1 [S1].

 

 

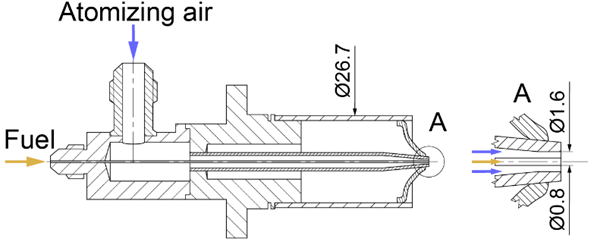
Fig.1: Sectional view of air blast atomizer.

 

Brief introduction of the research place

In the last five years, the Department of Energy Engineering has conducted deeper research into the atomization process. Due to the limited availability of advanced measurement technology in Hungary, the research is carried out mainly at Brno University of Technology where the properties of spray were examined with Phase Doppler Anemometry (PDA). The applied PDA is shown in Figure 2 [L1]. In addition, KFKI (MTA Wigner RCP) provides the option of applying Particle Image Velocimetry (PIV) [L2].

 

 

 

Fig. 2: The PDA setup.

 

History and context of the research

The research process began in the final semester of my BSc course when we started to deal with the problems of evaporation of renewable liquid fuels with Viktor Józsa. Based on the evaporation models learned during the course, it has become apparent that the process is strongly influenced by the quality of spraying. Therefore, in the summer of 2015 tests were carried out on diesel fuel at Brno University of Technology Spray Laboratory. The main direction of analyzes was the mapping of the velocity field and the determination of the droplet size distribution which was compared with a primitive numerical simulation. My MSc research work was awarded with the 1st prize of the Institutional Scientific Students’ Associations [L3].

 However, for the effective characterization of the spray, it is necessary to describe the probability density functions that characterize the distribution of droplets with outstanding fitting efficiency. In turn, detection of unimodal functions that provide the right fit is insufficient to improve the quality of atomization since their parameter dependence prevents the modelling of the processes in reality. As a function of this, the correlation analysis of the parameters was performed using the appropriate probability density functions with dimensionless numbers based on real measurement results. From the above-mentioned study, I was also awarded with the 1st prize of the Institutional Scientific Students’ Associations as an MSc student [L4].

Research goals, open questions

The main purpose of the research is to characterize the spray generated by the air blast atomizer, thereby provide optimum operating and physical parameters to maximize the efficiency of combustion [H1]. However, it requires a combination of analytical and numerical validation of the measurement results. There are only empirical and semi empirical formulas available to describe the formation of the spray. Nevertheless, their applications are questionable above the critical atomization pressure [H2, H3]. Thus, probability density functions that are used for the general description of the spray have to be able to trace the real measurement results with outstanding fit [L5]. Assignment of the parameters in the relations with dimensionless numbers which depend on the atomization pressure can be a solution in the global description of the spray. However, the form of relations created by correlation analysis is currently too complex for their widespread application and dissemination, so a significant, well-established reduction of correlations is required. In order to ensure the credibility of the global relations, the implementation of theory of confidence that is based on the use of statistical methods is currently under development.

The questions to be answered include the determination of minimum sampling rate since this is an indispensable input parameter for the efficient and credible execution of measurements [H4]. Based on our preliminary expectations, the sampling rate is strongly dependent on the quantity to be measured and on its intended way of use. In order to prove this, a user code has been developed and the evaluations are currently in process.

Application of the modified fractal theory raises further questions. Since the individual classes – unlike in the original idea – are measured along logarithmic scale, it is found that the function has several break points near the atomizer nozzle, while further away the breakpoints diminish and their numbers are minimized. Consequently, the primary spraying process could not have completed in the initial stage and the properties of the resulting spray are affected by several physical processes; while at the distant point we can find a developed spray. Function fitting showed that a tangent hyperbolic function is capable of describing the distribution of droplet sizes with outstanding efficiency, so this can solve our density function simplification problem. Primitive results from the theory are presented in Figure 3.

 

 

 

Fig. 3: The use of fractal theory for droplet size distribution.

 

Methods

Fitting probability density functions

The fitting of density functions is a result of selection performed by a given system of criteria. As a first step, classifying the representative mean diameters derived from the measurement into droplet size classes will allow us mapping their relative frequency using a histogram. During the function fitting to results obtained from the structural organization, those with outstanding fit efficiency are selected and subjected to further investigation. The applied method is based on the least square algorithm. The test is exacerbated by density functions that are only able to appropriately describe the droplet size distribution in certain spray pressure regimes or only in different spray regions. Therefore, the selected density functions are required to produce an outstanding fit for all measurement points in the spray [H5]. In the selection process, three probability density functions were selected, as described in Equations 1 - 3.

 

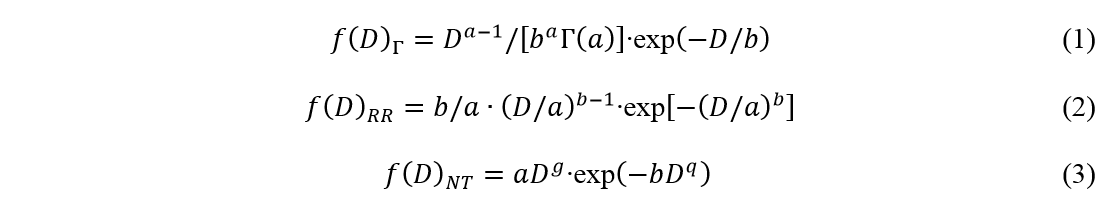
Application and extension of modified fractal theory

Based on literature, this type of spray test method has not been used as yet, so it can create a new way of mapping the spraying process. It is based on fractal theory where in our case, the derived representative diameters are sorted by size, where the droplet sizes are represented as relational relationships. According to the modified fractal theory, logarithmic representation is applied on both axes by which we can deduce the level of development of spray and the physical processes that are going on, based on the number of breakpoints in the function. The described phenomenon is shown in Figure 4.

 

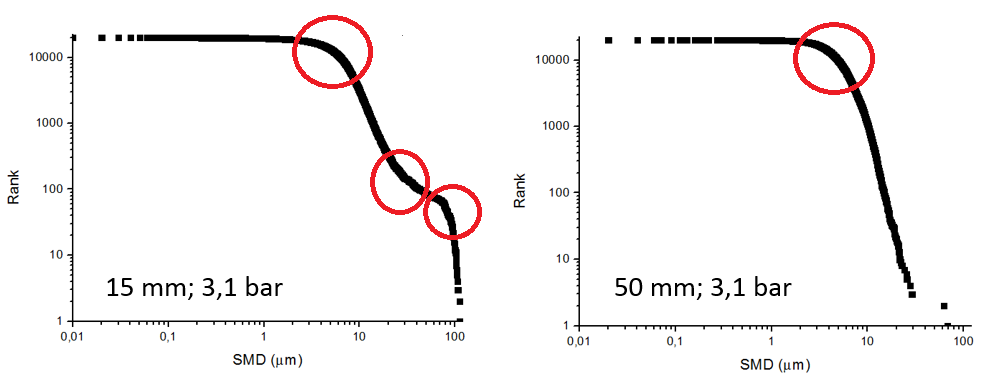
Fig. 4: Breakpoints from the modified fractal theory.

 

The method can be extended by applying the principle of Maximum Entropy (ME), which is not yet widely applied. The applicability of the method requires the knowledge on two representative droplet diameters; and indeed, they will be obtained from the modified fractal theory.

Symmetry of spray

Analyzes of spray symmetric behavior are important aspects of the manufacturing technology of the atomizers. For this purpose, the spray implementation is required into cylindrical coordinate system, where the tests are carried out using a finite difference method. The basics of the method are provided by the use of the continuity equation and the Equation 4 and its expanded form in Equation 5.

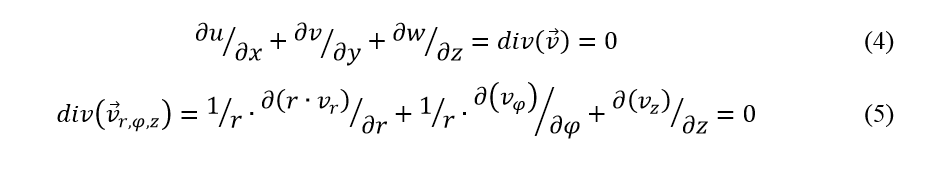
Development of user code

To evaluate measurement series to more quickly, a user code has been written, which is expanded ongoing as new knowledge and methods are available [H6]. The whole set of applied methods developed so far has been implemented in the program, which can be applied globally. An illustrated picture shows the created program in Figure 5 [S2, S3, S4]..

 

 

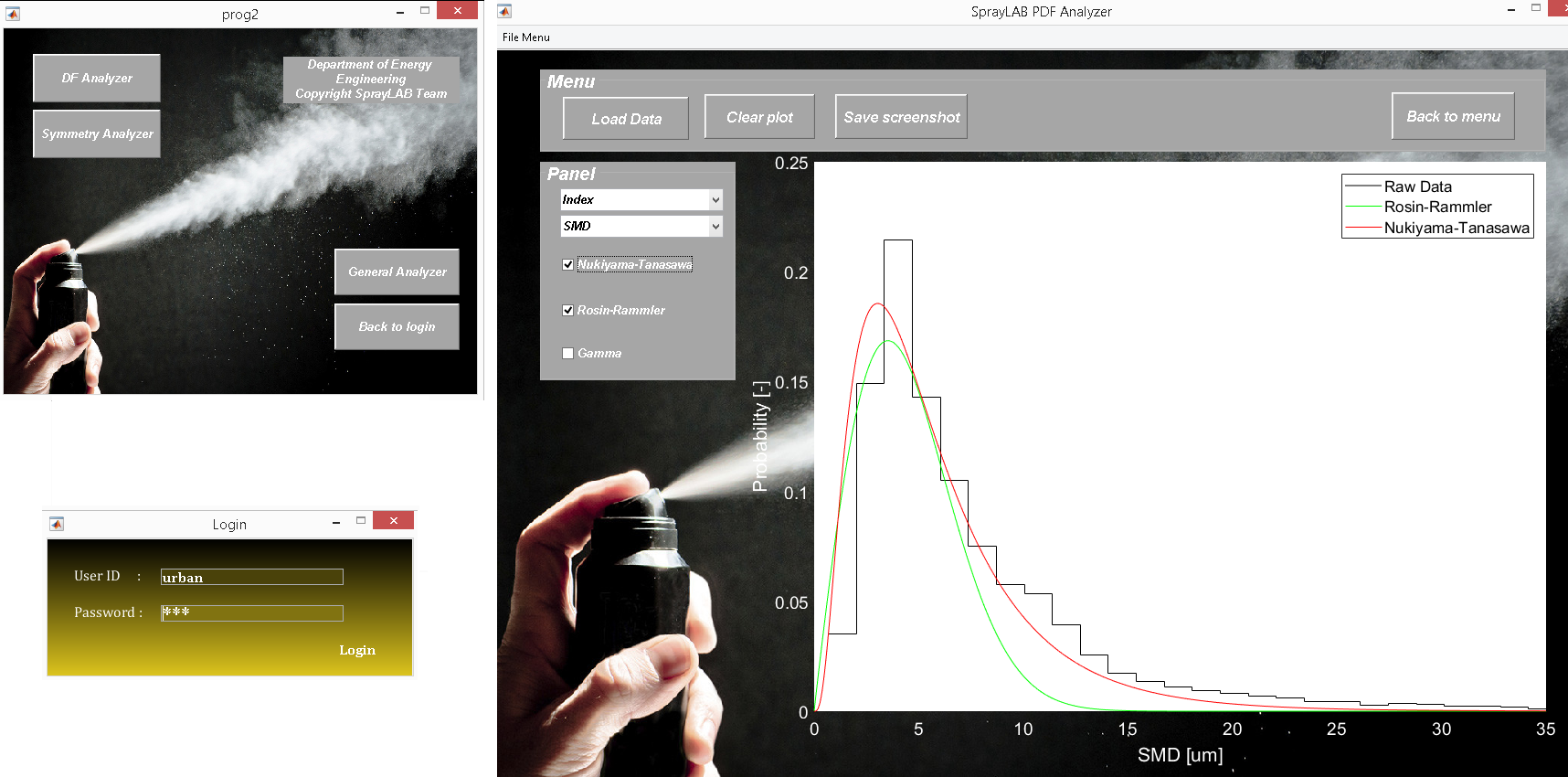
Fig. 5: A user program written in MATLAB software environment.

 

Numerical simulation

To evaluate and easily manage spray test methods globally for any type of fuel, the methods presented and applied so far need to be supported by numerical simulations. In the currently available literature, none of the statements regarding the numerical simulation of the spray generated by the air blast atomizer can be considered a validated model in the absence of results from the methodological analyzes listed above. Thus in the future, implementation of several spraying descriptions will be required to validate with a finite volume-based method.

Results

The results achieved so far are presented below in thematic grouping.

The analyzes are based on a software code written in MATLAB software environment, which enabled the evaluation of the quality of the density functions that build on each statistical basics. Analyzing the relative frequency of droplet size classes on each atomization pressure, the parameters of the probability density functions that proved to be appropriate were further examined. After collecting the obtained parameters, I conducted a trend analysis and the results were compared with the trends of dimensionless numbers, so I determined the ability to fit for the most suitable pairs of parameter [H7]. During the fitting, all relevant measurement points which were located at the spray were subjected to the examination. So, the three density functions presented earlier were given by different kind of dimensionless numbers. The resulting relations are included in Equations 6 – 8 [L4].

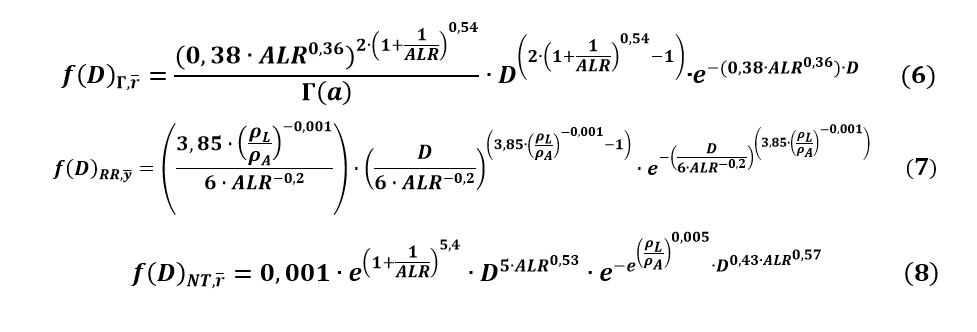
The fitted dimensionless numbers were supplemented with upper and lower confidence limits as a function of the atomization pressure. Based on the validation rates generated by the PDA's BSA Flow v5.2 software, a ± 20% credibility range was proved to be adequate for the entire spray [S4, S5]. The parameter changes were appropriately fitted to this band, despite the fact that the measurement had significant sources of error. The change of parameters and the trend of the dimensionless numbers were compared using a correlation function where I expected a minimum of 80% correlation. The minimum number of points that did not met the condition were removed because the parameters that did not clearly fit in the series of measurements would have had a negative impact on my final results [S2, L4].

 

 

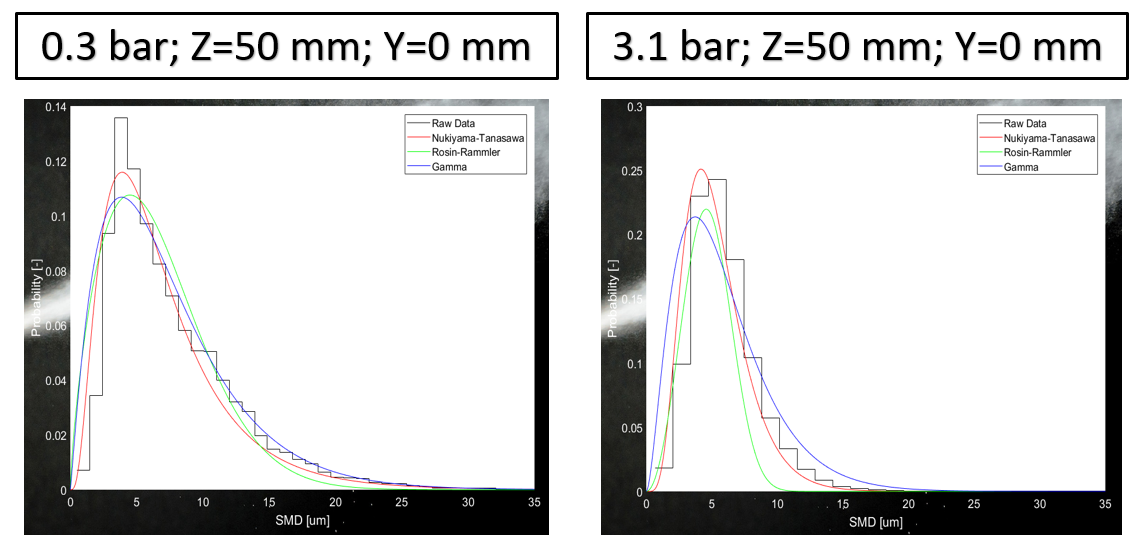
Fig. 6: Apply the three outstanding density functions in the program.

 

The fitting of density functions described above to the real measurement results can provide further guidance on their fitting efficiency. So the probability density functions are presented in Figure 6. at two different extreme cases, with the same local boundary condition. Having reviewed every local point of the large data set available, it can be shown that presentation of results require only presenting them at a randomly selected single point, since each point is representative in the global spray. Based on the results so far, the analyzed parameters have been weighted with the data rate, so error bars indicate the weighted deviation. Improvement of fitting quality of was achieved by increasing the atomization pressure, which is explained by the increasingly homogeneous nature of the spray. The best curve fitting was produced by the Γ probability density function on average (R² = 0.983) and the worst was the Rosin-Rammler (R² = 0.962) but this cannot considered completely wrong with respect to the entire spray. Nevertheless, in the range of lower atomization pressures, Nukiyama-Tanasawa (R² = 0.982) produced a better curve fit. However, in the supersonic pressure regime, the Γ was clearly better. Due to this result, it is worth examining the real sprays for two extreme atomization pressures which are shown in Figure 7. together with the qualitative assessment [S1].

 

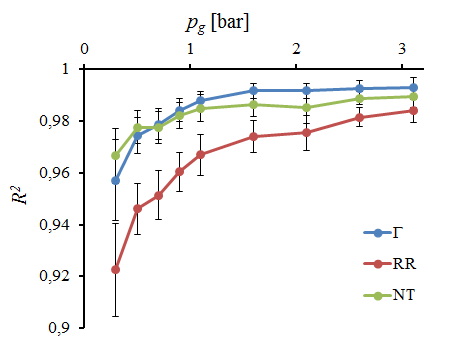
Fig. 7: Quality assessment of density functions and the presentation of extreme sprays.

Expected impact and further research

As a first-year PhD student I currently have three publications which can be linked to thesis points and two additional publications are under revision. Of these, the D1, Q1 certified (IF = 2.25) International Journal of Multiphase Flow is outstanding [S1]. In addition, I have two draft publications, which are currently being drafted. One of them is a summary of the minimum sampling number for measurable quantities, while the other focuses on the efficiency of atomization, self-similarity of the free jet and turbulent kinetic energy [H8, H9, H10].

In parallel with the measurements and modeling tasks, the numerical simulation of the process is also developed with promising results so far, but due to the several simplification assumptions it has no scientific value [L3, S6]. However, implementing the globally descriptive relations into a finite volumetric method will provide an opportunity to numerically underpin the complex process of atomization in the future. Nevertheless, this is an indispensable prerequisite for further measurements in the future, where I mainly focus on the examination of vegetable oils with high viscosity.

In summary, after the validation of analytical and numerical results based on the measurement results, the finding may be valuable for engineers conducting research and application in the spraying area.

 

Publications, references, links

Publications.

 

[S1] - András Urbán, Matouš Zaremba, Milan Malý, Viktor Józsa, Jan Jedelský - Droplet dynamics and size characterization of high-velocity airblast atomization (2017), International Journal of Multiphase Flow 95: pp. 1‑11. doi.org/10.1016/j.ijmultiphaseflow.2017.02.001

 

[S2] - András Urbán, Viktor Dr. Józsa - Investigation of fuel atomization with density functions (2017), Periodica Polytechnica Mechanical Engineering (submitted)

 

[S3] - Urbán András - Atmoszférikus tüzelőanyagpermet vizsgálata sűrűségfüggvényekkel (in Hungarian) (2017),: OGÉT 2017: XXV. Nemzetközi Gépészeti Találkozó = 25th International Conference on Mechanical Engineering, At 436-439, Volume: 500

 

[S4] - Józsa Viktor, Urbán András - Egyszerű sugaras levegő segédközeges porlasztó Sauter közepes cseppátmérőjének mérése és becslése (in Hungarian) (2016), Energiagazdálkodás 57:(3-4) pp. 12-16.

 

[S5] - Urbán András, Matouš Zaremba, Milan Malý, Jan Jedelský, Dr. Józsa Viktor - Atmoszférikus tüzelőanyag permet Fázis Doppler Anemométeres mérési bizonytalanságának elemzése (in Hungarian) (2017), Energiagazdálkodás (submitted)

 

[S6] - Urbán András - Levegő segédközeges porlasztó vizsgálata fázis Doppler anemométer segítségével (in Hungarian) (2016), III. BME Gépész Szakmai Konferencia

 

Links.

 

[L1] - PDA

[L2] - PIV

[L3] - TDK 2015: Levegő segédközeges porlasztó vizsgálata Fázis Doppler Anemométer segítségével

[L4] - TDK 2016: Egyszerű sugaras levegő segédközeges porlasztás cseppméret eloszlásának vizsgálata

[L5] - Sűrűségfüggvény

 

References.

 

[H1] - Rizk, N.K., Lefebvre, A.H., 1984. Spray characteristics of plain-jet airblast atomizers. J. Eng. Gas Turbines Power 106, 634–638.

 

[H2] - Babinsky, E., Sojka, P.E., 2002. Modeling drop size distributions. Prog. Energy Combust. Sci. 28, 303–329. doi:10.1016/S0360-1285(02)00004-7.

 

[H3] - Liu, H.-F., Gong, X., Li, W.-F., Wang, F.-C., Yu, Z.-H., 2006. Prediction of droplet size distribution in sprays of prefilming air-blast atomizers. Chem. Eng. Sci. 61, 1741– 1747. doi:10.1016/j.ces.2005.10.012.

 

[H4] - Lefebvre, A.H., 1989. Atomization and Sprays. Hemisphere Publishing Corporation.

 

[H5] - Xiangui, L., Tankin, R.S., 1987. Droplet size distribution: a derivation of a NukiyamaTanasawa type distribution function. Combust. Sci. Technol. 56, 65–76. doi:10. 1080/00102208708947081.

 

[H6] - Brena˜ de la Rosa, A, Wang, G., Bachalo, W.D., 1992. The effect of swirl on the velocity and turbulence fields of a liquid spray. J. Eng. Gas Turbines Power 114, 72–81.

 

[H7] - Lefebvre, A.H., 1980. Airblast atomization. Prog. Energy Combust. Sci. 6, 233–261. doi:10.1016/0360-1285(80)90017-9. Lefebvre, A.H., Ballal, D.R., 2010. Gas Turbine Combustion, Third. Ed. CRC Press, Boca Raton.

 

[H8] - Lefebvre, A.H., 1992. Energy considerations in twin-fluid atomization. J. Eng. Gas Turbines Power 114, 89–96.

 

[H9] - Jedelsky, J., Jicha, M., 2014. Energy considerations in spraying process of a spill-return pressure-swirl atomizer. Appl. Energy 132, 485–495. doi:10.1016/j. apenergy.2014.07.042.

 

[H10] - Jedelsky, J., Jicha, M., 2013. Energy conversion during effervescent atomization. Fuel 111, 836–844. doi:10.1016/j.fuel.2013.03.053.