|
|
BMe Kutatói pályázat |
|
Pattantyús-Ábrahám Géza Gépészeti Tudományok Doktori Iskola
BME Gépészmérnöki Kar, Energetikai Gépek és Rendszerek Tanszék
Témavezető: Dr. Sztankó Krisztián
Levegő segédközeges porlasztás permetének jellemzése
A kutatási téma néhány soros bemutatása
Doktori kutatómunkám célja a levegő-segédközeges porlasztó által generált permet jellemzése korszerű méréstechnikai eszközök bevonásának segítségével. A permet jellemzése és a porlasztás folyamatának analitikus és numerikus modellezése teret nyithat a folyékony tüzelőanyagok hatékonyabb felhasználásának, különös tekintettel a magas viszkozitású növényi olajokra (repce-, napraforgó olaj). A szemléltetés érdekében kerül bemutatásra az 1. ábrán az alkalmazott porlasztótípus [S1].
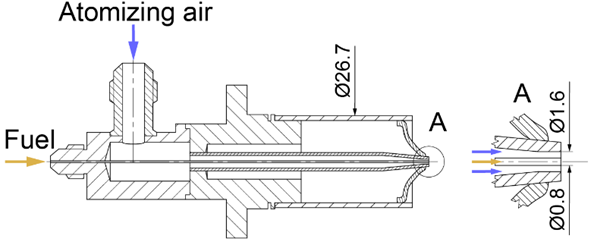
1. ábra: A levegő-segédközeges porlasztó metszeti rajza
A kutatóhely rövid bemutatása
A BME Energetikai Gépek és Rendszerek Tanszéken az utóbbi öt évben lendült fel újra a porlasztás folyamatának mélyebb kutatása. A hazai viszonylatban csak korlátozottan rendelkezésre álló korszerű méréstechnikai eszközök miatt a kutatás főként a Brnoi Műszaki Egyetemen zajlik, ahol Fázis Doppler Anemométer (PDA) segítségével vizsgáljuk a kialakult permet tulajdonságait. Ennek érdekében kerül bemutatásra a 2. ábrán az alkalmazott PDA [L1]. Továbbá a KFKI is lehetőséget biztosít a Particle Image Velocimetry (PIV) alkalmazására [L2].

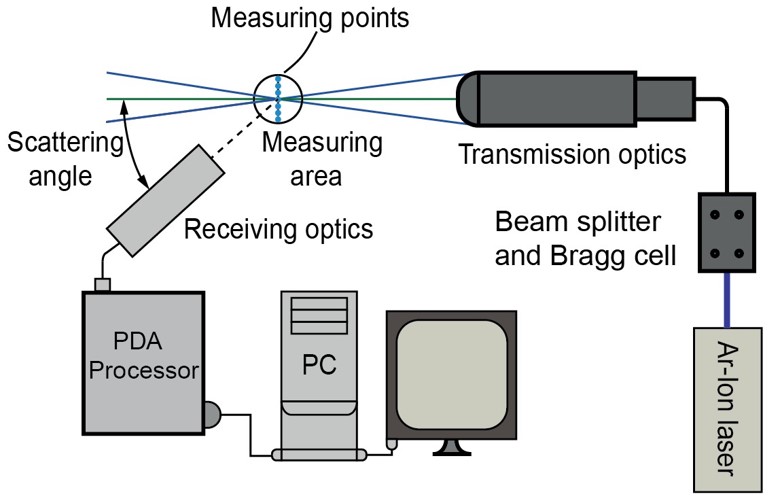
2. ábra: A PDA összeállítása
A kutatás történetének, tágabb kontextusának bemutatása
A kutatási folyamat a BSc képzésem záró félévében kezdődött el, amikor Józsa Viktorral megújuló folyékony tüzelőanyagok párolgásának problémáival kezdtünk el foglalkozni. Az itt megismert párolgási modellek alapján beláthatóvá vált, hogy a folyamatot erősen befolyásolja a porlasztás minősége, így 2015 nyarán a Brnoi Műszaki Egyetem Permetvizsgáló Laborjában vizsgálatokat végeztünk diesel tüzelőanyagra vonatkozóan. Az elemzések fő irányvonalát a sebességmező feltérképezése és a cseppméret-eloszlások meghatározása alkotta, amely egy kezdetleges numerikus szimulációval került összevetésre. A kutatómunkából MSc hallgatóként Intézményi TDK I. helyezést értem el [L3].
Azonban a permet hatékony jellemzéséhez olyan valószínűségi sűrűségfüggvények leírására van szükség, melyek kiemelkedő illeszkedési hatékonysággal lekövetik a cseppméretek eloszlását. A megfelelő illeszkedést biztosító unimodális függvények felderítése viszont nem elegendő a porlasztás minőségi javításához, mivel ezek paraméterfüggősége lehetetlenné teszi a valóságban lezajló folyamatok modellezését. Ennek függvényében a paraméterek korrelációs analízisét elvégezve valós mérési eredményekre épülő dimenziótlan számokkal kerültek felruházásra a megfelelő sűrűségfüggvények. Az előbbiekben ismertetett tanulmányból MSc hallgatóként ugyancsak Intézményi TDK I. helyezést értem el [L4].
A kutatás célja, a megválaszolandó kérdések.
A kutatás fő célja a levegő-segédközeges porlasztó által generált permet karakterisztikus jellemzése, ezen keresztül optimális üzemi és fizikai paraméterek biztosítása az égési hatásfok maximalizálásának érdekében [H1]. Ehhez azonban a mérési eredmények analitikus és numerikus validációjának együttese szükséges.
A képződő permet leírására jelenleg is csak empirikus és félempirikus formulák állnak rendelkezésre, melyek alkalmazása a kritikus porlasztási túlnyomás feletti tartományban megkérdőjelezhető [H2, H3]. Így a permet általános leírásának érdekében olyan valószínűségi sűrűségfüggvények kerülnek alkalmazásra, amelyek képesek kiemelkedő illeszkedési hatékonysággal lekövetni a valós mérési eredményeket [L5]. Az összefüggésekben szereplő paraméterek porlasztónyomástól függő dimenziótlan számokkal történő felruházása megoldást jelenthet a permet globális leírásában. A korrelációs analízis segítségével megalkotott összefüggések formája azonban jelenleg túl bonyolult azok széleskörű alkalmazásához és elterjedéséhez, így az összefüggések jelentős mértékű, megalapozott redukálása szükséges. A megalkotott globális összefüggések hitelességének biztosítása érdekében a statisztikai módszerek felhasználására építő konfidenciasáv-elmélet jelenleg is kidolgozás alatt áll.
A megválaszolandó kérdések közé tartozik a minimális mintavételezési szám meghatározása is, mivel a mérések hatékony és hiteles kivitelezéséhez ez elengedhetetlen bemeneti paramétert képez [H4]. Az előzetes várakozásunk és az eddig szerzett tapasztalataink alapján a mintavételezési szám erősen függ a vizsgálni kívánt mérendő mennyiségtől és annak felhasználási módjától. Ennek bebizonyítása érdekében felhasználói programkód került fejlesztésre, és a kiértékelések jelenleg is folynak.
További kérdéseket vet fel a módosított fraktálelmélet alkalmazása, hiszen ha az eredeti elgondolástól eltérően az egyedosztályok is logaritmikus skálára kerülnek, akkor azt tapasztaljuk, hogy a porlasztó fúvókája közvetlen közelében a függvény több törésponttal is rendelkezik, míg a porlasztó fúvókájától távolodva a töréspontok kisimulnak, és számuk minimalizálódik. Ebből arra lehet következtetni, hogy a kezdeti szakaszban a primer porlasztási folyamat még nem fejeződött be, és több fizikai folyamat is befolyásolja a képződő permet tulajdonságait, míg a távolabbi pontban már egy kifejlett permetet tapasztalhatunk. A módszerből fakadó eredményre történő függvényillesztés kiemelkedő hatékonysággal bebizonyította, hogy egy tangens hiperbolikusz függvény képes leírni a cseppméretek eloszlását, amely megoldást jelenthet a sűrűségfüggvények egyszerűsítésében. Az elméletből származó kezdetleges eredmények a 3. ábrán kerülnek bemutatásra.
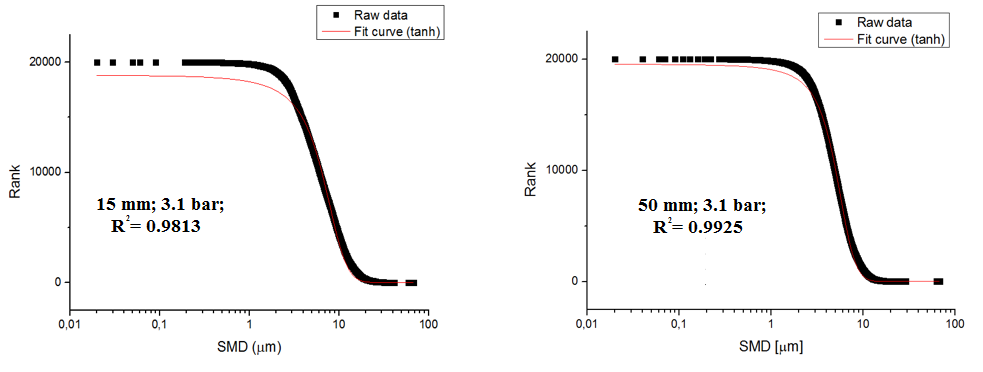
3. ábra: A fraktálelmélet alkalmazása cseppméret-eloszlásra vonatkozóan
Módszerek
Valószínűségi sűrűségfüggvények illesztése
A sűrűségfüggvények illesztése meghatározott szempontrendszer szerinti szelekció eredményeként valósul meg. Első lépésként a mérésből származtatott reprezentatív középátmérők cseppméret-osztályokba történő besorolásával lehetőség nyílik azok relatív gyakoriságának feltérképezésére hisztogram segítségével. A strukturális rendszerezésből származó eredményekre történő függvényillesztés során a kiemelkedő illeszkedési hatékonysággal rendelkezők kiválasztásra kerülnek, és ezeket további vizsgálatoknak vetjük alá. Az illesztések során alkalmazott algoritmus alapját a legkisebb négyzetek módszere adja. A vizsgálatot nehezítik az olyan sűrűségfüggvények, amelyek csak bizonyos porlasztónyomás tartományokban vagy csak különböző permetrégiókban képesek megfelelő módon leírni a cseppméret-eloszlást. Ennek elkerülése érdekében elvárás, hogy a kiválasztott sűrűségfüggvények a permetben található összes mérési pontra kiemelkedő illeszkedést produkáljanak [H5]. A szelekció során a következő három valószínűségi sűrűségfüggvény került kiválasztásra, amely az 1–3. egyenletekben kerültek leírásra.
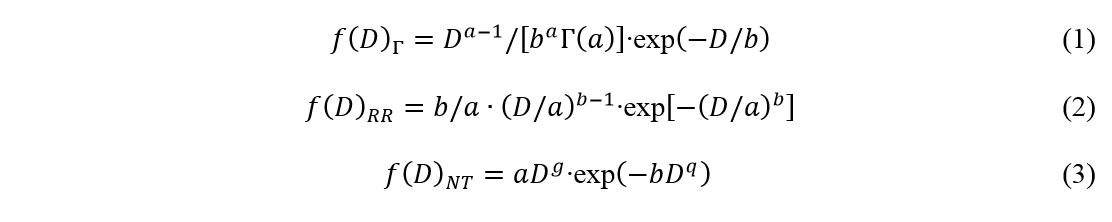
Módosított fraktálelmélet alkalmazása és kiterjesztése
A jelenlegi irodalom alapján ez a típusú permetvizsgálati módszer nem alkalmazott, így egy új utat teremthet a permetképződés folyamatának feltérképezésében. Alapját a fraktálelmélet adja, ahol a mi esetünkben a származtatott reprezentatív átmérők nagyság szerinti sorba rendezése történik, ahol relációs kapcsolatként kerülnek ábrázolásra a cseppméretek. A módosított fraktálelmélet értelmében mindkét tengelyen logaritmikus ábrázolás kerül alkalmazásra, mellyel a permet fejlettségére és a lejátszódó fizikai folyamatok számára tudunk következtetni a függvényben található töréspontok számából. A leírt jelenséget a 4. ábra mutatja.
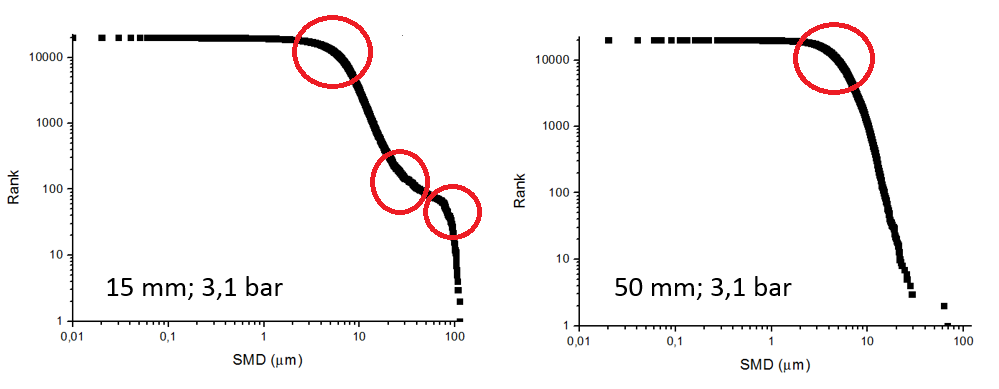
4. ábra: A módosított fraktálelméletből származó töréspont detektálások
A módszer kiterjeszthető a jelenleg még nem széleskörűen alkalmazott Maximum Entrópia (ME) elvének alkalmazásával. A módszer alkalmazhatóságának feltétele, hogy ismert legyen két reprezentatív cseppátmérő, amely a módosított fraktálelmélet alkalmazásából fakadóan adottá válik.
Permetszimmetria vizsgálata
A porlasztók gyártástechnológiájának szempontjából fontos vizsgálati szempontot képeznek a permet szimmetrikus viselkedésre vonatkozó elemzések. Ehhez a permet henger koordinátarendszerbeli implementálásra van szükség, ahol a vizsgálatok véges differencia módszer segítségével kerültek kivitelezésre. A módszer alapjait a kontinuitás tétel felhasználása szolgáltatja, illetve a 4. egyenletben és az ebből származtatott 5. egyenletben található összefüggések.
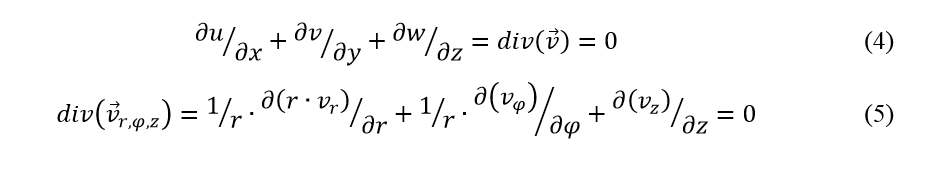
Felhasználói programkód fejlesztése
Annak érdekében, hogy az egyes mérési sorozatok gyorsabban kerüljenek kiértékelésre felhasználói programkód került megírásra, amely az új ismeretek és módszerek megalkotásával folyamatosan bővül [H6]. Az eddig alkalmazott módszerek összessége implementálásra került a programba, amely globális jelleggel alkalmazható. Az 5. ábrán szemléltető képen kerül bemutatásra a megalkotott program [S2, S3, S4].
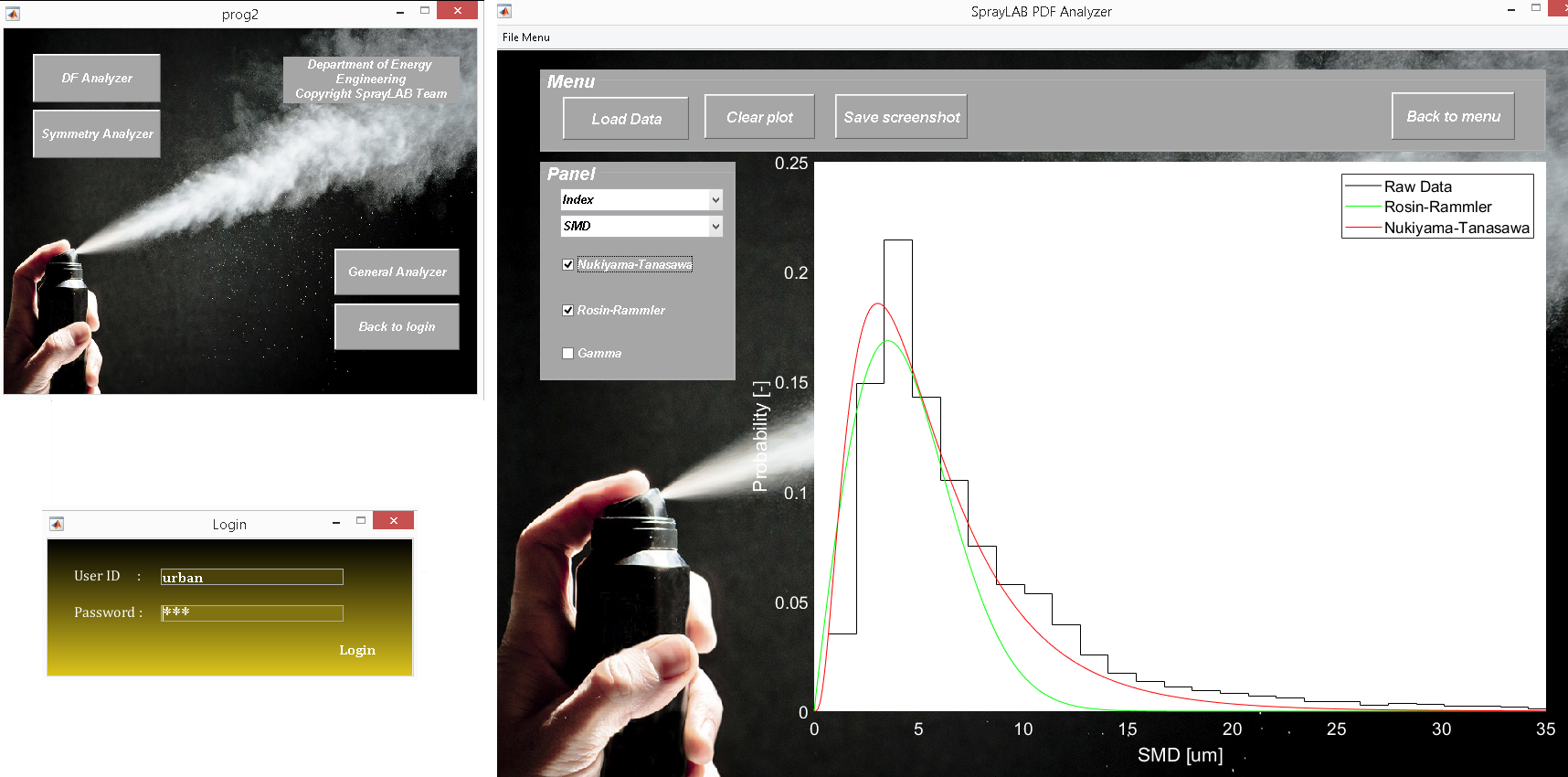
5. ábra: A MATLAB szoftverkörnyezetben írt felhasználói program
Numerikus szimuláció
Annak érdekében, hogy a permetvizsgálati módszerek globális jelleggel bármilyen tüzelőanyagfajtára kiértékelhetővé és könnyen kezelhetővé váljanak az eddig bemutatott és alkalmazott módszereket numerikus szimulációval szükséges alátámasztani. A jelenleg rendelkezésre álló irodalomban – annak ellenére, hogy találhatóak a levegő-segédközeges porlasztó által generált permet numerikus szimulációjára vonatkozó megállapítások – egyik sem tekinthető validált modellnek az előbbiekben felsorolt módszertani elemzésekből származó eredmények hiányában. Így, a jövőben számos, permetképződés leírására vonatkozó összefüggés implementálására lesz szükség a véges térfogat alapú módszerrel történő validálás érdekében.
Eddigi eredmények
Az eddig elért eredmények alábbi bemutatása tematikus csoportosítás szerint történik.
Az elemzések MATLAB szoftverkörnyezetben írt programkódokra építenek, melyek segítségével lehetőségem volt az egyes statisztikai alapokra épülő sűrűségfüggvények minőségi értékelésére. Az egyes porlasztónyomásokon kialakuló cseppméret osztályok relatív gyakoriságának elemzésén keresztül vizsgálat alá kerültek a megfelelőnek bizonyuló valószínűségi sűrűségfüggvények paraméterei. A kapott paraméterek összegyűjtése után trendanalízist végeztem, melynek eredményei összevetésre kerültek a dimenziótlan számok változásának trendjeivel, így a legjobban illeszkedő paraméterpárosok illeszthetőségét állapítottam meg [H7]. Az illesztések során a permetben jelenlévő összes releváns mérési pont vizsgálat alá került, melyeken a korábban bemutatott három sűrűségfüggvény dimenziótlan számokkal való felruházását végeztem el. A kapott összefüggéseket a 6–8. egyenletek tartalmazzák [L4].
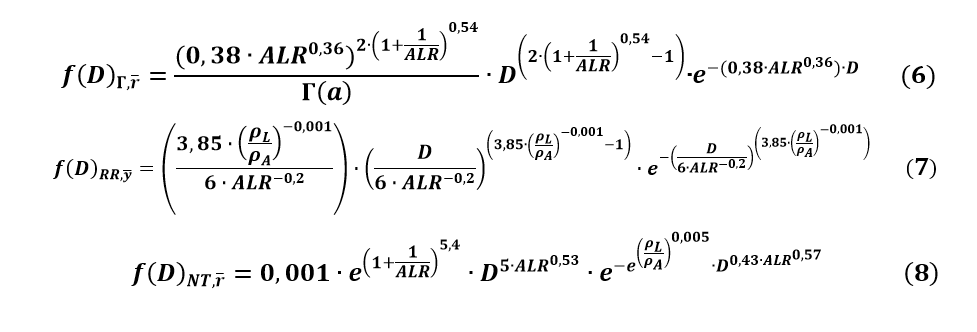
Az egyes sűrűségfüggvény-paraméterek változására illesztett dimenziótlan számok felső és alsó konfidenciasávval kerültek kiegészítésre a porlasztónyomás függvényében. A PDA BSA Flow v5.2 szoftvere által generált validációs ráták alapján ±20%-os érvényességi tartomány került bevezetése, amely megfelelőnek bizonyult a teljes permetre vonatkozóan [S4, S5]. A paraméterek változásai megfelelő módon illeszkedtek ebbe a sávba, annak ellenére, hogy a mérés jelentős mértékű hibaforrásokat hordozott magában. A paraméterek változása és a dimenziótlan számok trendje korrelációs függvény segítségével került összehasonlításra, ahol minimálisan 80%-os korrelációt vártam el. A feltételt nem teljesítő, minimális számban jelenlévő pontok eltávolításra kerültek, mivel a mérési sorozatba egyértelműen nem illeszkedő paraméterek negatív hatással lettek volna a végső konklúzióból származó eredményeimre [S2, L4].
6. ábra: A három kiemelkedő sűrűségfüggvény alkalmazása a programban
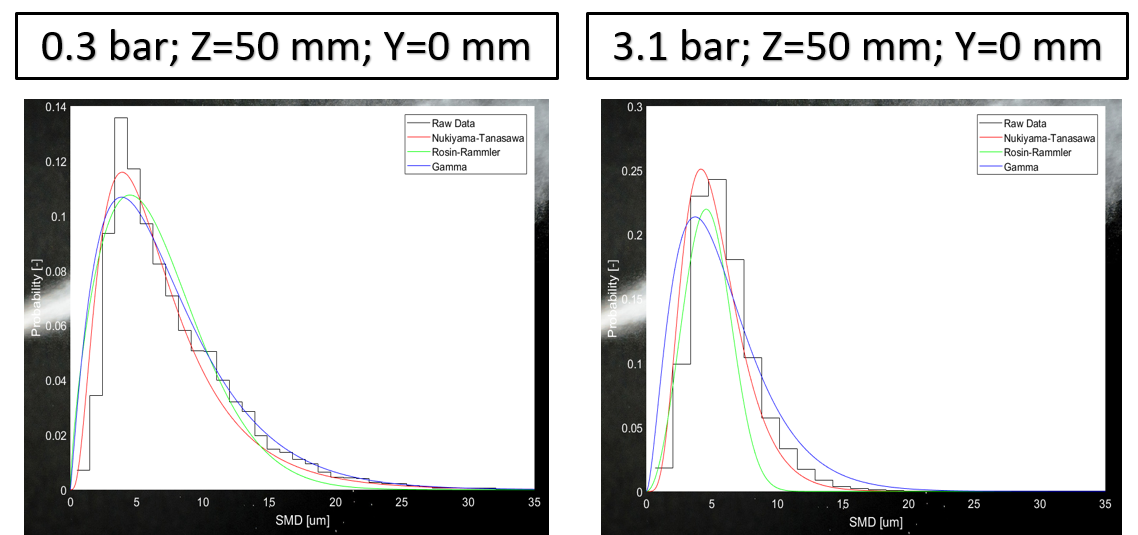
Az előbbiekben vizsgált sűrűségfüggvények valós mérési eredményekre való illesztése, további iránymutatást adhat azok illesztési hatékonyságáról, így a 6. ábrán két különböző, szélsőséges esetben, azonban azonos peremfeltétellel rendelkező lokális pontban kerülnek bemutatásra a valószínűségi sűrűségfüggvények. A rendelkezésre álló nagymennyiségű adathalmaz minden lokális pontját megvizsgálva belátható, hogy az elemzések bemutatásához elegendő egy véletlenszerűen kiválasztott pontban bemutatni az eredményeket, mivel minden pont reprezentatív a globális permetre nézve. Az eddigi eredményekből fakadóan a vizsgált paraméterek súlyozásra kerültek az adatrátával, így a hibasávok jelzik a súlyozott szórást. A legjobb illesztést Gamma segítségével értem el, melynél az illeszkedés minősége átlagosan 0,983-ra adódott, felülmúlva a Rosin-Rammler (R2=0,962) és a Nukiyama-Tanasawa (R2=0,982) valószínűségi sűrűségfüggvényeket. Az illeszkedés minőségének javulása a porlasztónyomás növelésével valósult meg, amire a permet egyre homogénebb jellege szolgál magyarázattal. Megfigyelhető, hogy alacsonyabb porlasztónyomások esetében a Nukiyama-Tanasawa, míg a kritikus porlasztónyomás felett egyértelműen a Gamma függvény produkálja a jobb illeszkedést. Ebből az eredményből fakadóan érdemes megvizsgálni a valós permetképeket két szélsőséges porlasztási túlnyomás esetében, amely a 7. ábrán látható a minőségi értékeléssel egyetemben [S1].
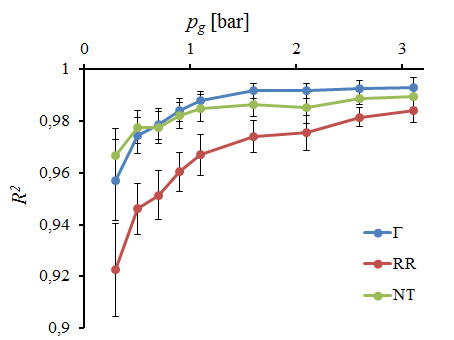

7. ábra: A sűrűségfüggvények minőségi értékelése és a szélsőséges permetképek
Várható impakt, további kutatás
Első féléves doktorandusz hallgatóként jelenleg három olyan publikációval rendelkezem, amely tézispontokhoz köthető, emellett még további két publikáció is be van nyújtva. Ezek közül kiemelkedő a D1, Q1 minősítésű (IF =2.25) International Journal of Multiphase Flow folyóirat [S1]. Rendelkezem továbbá két publikációtervezettel is, melyek kidolgozása jelenleg is folyamatban van. Ezek közül az egyik a minimális mintavételezési szám mérendő mennyiségre vonatkozó értékek összefoglalását tartalmazza, míg a másik a porlasztás hatásfokára, a szabadsugár önhasonlósági vizsgálatára, illetve a turbulens kinetikus energiára fókuszál [H8, H9, H10].
A mérések és a modellillesztési feladatok kivitelezése mellett párhuzamosan kerül fejlesztésre a lejátszódó folyamat numerikus szimulációja is, amely bár az eddigi eredmények alapján bizakodásra ad okot, több egyszerűsítő feltételezésből fakadóan azonban még nincs tudományos értéke [L3, S6]. Azonban a globálisan leíró összefüggések véges térfogatos módszerbe történő implementálásával a jövőben lehetőség nyílik numerikusan is a porlasztás komplex folyamatát alátámasztani. Ennek azonban elengedhetetlen feltétele a további mérések kivitelezése a jövőben, ahol főként a magas viszkozitással rendelkező növényi olajok vizsgálata a célom. Összességében, ha az analitikus és numerikus eredmények validálásra kerülnek a mérési eredmények alapján, akkor az eredmények a porlasztás területét kutató és alkalmazó mérnökök számára jelentőséggel bírhat.
Saját publikációk, hivatkozások, linkgyűjtemény
Kapcsolódó saját publikációk listája.
[S1] - András Urbán, Matouš Zaremba, Milan Malý, Viktor Józsa, Jan Jedelský - Droplet dynamics and size characterization of high-velocity airblast atomization (2017), International Journal of Multiphase Flow 95: 1-11. oldal, doi.org/10.1016/j.ijmultiphaseflow.2017.02.001
[S2] - András Urbán, Viktor Dr. Józsa - Investigation of fuel atomization with density functions (2017), Periodica Polytechnica Mechanical Engineering (Benyújtva)
[S3] - Urbán András - Atmoszférikus tüzelőanyagpermet vizsgálata sűrűségfüggvényekkel (2017),: OGÉT 2017: XXV. Nemzetközi Gépészeti Találkozó = 25th International Conference on Mechanical Engineering, 436-439. oldal, 500. kötet
[S4] - Józsa Viktor, Urbán András - Egyszerű sugaras levegő-segédközeges porlasztó Sauter közepes cseppátmérőjének mérése és becslése (2016), Energiagazdálkodás 57:(3–4) 12–16. oldal
[S5] - Urbán András, Matouš Zaremba, Milan Malý, Jan Jedelský, Dr. Józsa Viktor - Atmoszférikus tüzelőanyag permet Fázis Doppler Anemométeres mérési bizonytalanságának elemzése (2017), Energiagazdálkodás (Benyújtva)
[S6] - Urbán András – Levegő-segédközeges porlasztó vizsgálata Fázis Doppler Anemométer segítségével (2016), III. BME Gépész Szakmai Konferencia
Linkgyűjtemény.
[L1] – PDA
[L2] – PIV
[L3] – TDK 2015: Levegő-segédközeges porlasztó vizsgálata Fázis Doppler Anemométer segítségével
[L4] – TDK 2016: Egyszerű sugaras levegő-segédközeges porlasztás cseppméret eloszlásának vizsgálata
[L5] – Sűrűségfüggvény
Hivatkozások listája.
[H1] - Rizk, N.K., Lefebvre, A.H., 1984. Spray characteristics of plain-jet airblast atomizers. J. Eng. Gas Turbines Power 106, 634–638.
[H2] - Babinsky, E., Sojka, P.E., 2002. Modeling drop size distributions. Prog. Energy Combust. Sci. 28, 303–329. doi:10.1016/S0360-1285(02)00004-7.
[H3] - Liu, H.-F., Gong, X., Li, W.-F., Wang, F.-C., Yu, Z.-H., 2006. Prediction of droplet size distribution in sprays of prefilming air-blast atomizers. Chem. Eng. Sci. 61, 1741– 1747. doi:10.1016/j.ces.2005.10.012.
[H4] - Lefebvre, A.H., 1989. Atomization and Sprays. Hemisphere Publishing Corporation.
[H5] - Xiangui, L., Tankin, R.S., 1987. Droplet size distribution: a derivation of a NukiyamaTanasawa type distribution function. Combust. Sci. Technol. 56, 65–76. doi:10. 1080/00102208708947081.
[H6] - Brena˜ de la Rosa, A, Wang, G., Bachalo, W.D., 1992. The effect of swirl on the velocity and turbulence fields of a liquid spray. J. Eng. Gas Turbines Power 114, 72–81.
[H7] - Lefebvre, A.H., 1980. Airblast atomization. Prog. Energy Combust. Sci. 6, 233–261. doi:10.1016/0360-1285(80)90017-9. Lefebvre, A.H., Ballal, D.R., 2010. Gas Turbine Combustion, Third. Ed. CRC Press, Boca Raton.
[H8] - Lefebvre, A.H., 1992. Energy considerations in twin-fluid atomization. J. Eng. Gas Turbines Power 114, 89–96.
[H9] - Jedelsky, J., Jicha, M., 2014. Energy considerations in spraying process of a spill-return pressure-swirl atomizer. Appl. Energy 132, 485–495. doi:10.1016/j. apenergy.2014.07.042.
[H10] - Jedelsky, J., Jicha, M., 2013. Energy conversion during effervescent atomization. Fuel 111, 836–844. doi:10.1016/j.fuel.2013.03.053.
