Pattantyús-Ábrahám Géza Gépészeti Tudományok Doktori Iskola 

BME Gépészmérnöki Kar, Gép- és Terméktervezés Tanszék

Témavezető: Dr. Kerényi György

Talaj diszkrét elemes modellezése talaj-kerék kölcsönhatásának elemzéséhez

A kutatási téma néhány soros bemutatása

A kutatási téma kohézív talajok modellezéséről szól: a talaj‒járókerék kölcsönhatását elemzi, elsősorban a kerék talajra gyakorolt hatásának numerikus modellezésének lehetőségét vizsgálva. A mezőgazdasági termelésben gyakran előforduló jelenség a talaj-kerék kölcsönhatása, hiszen az erőgépek a vonóerejüket a kerekeiken keresztül fejtik ki, miközben a talajt jelentős nyomó- és nyíró-igénybevételnek teszik ki. A traktorokon kívül a legtöbb mezőgazdasági munkagép is rendelkezik kerekes futóművel, amelyek szintén nyomással terhelik a talaj felső rétegeit.

Az utóbbi évtizedekben egyre nagyobb tömegű mezőgazdasági gépek jelentek meg a piacon, amelyek mind függőleges, mind vízszintes irányban nagyobb terhelést jelentek a talajokra. Ez ellentmond a környezetbarát, talajkímélő mezőgazdasági művelésben elvártaknak, ezért szükség van a jelenség részletes vizsgálatára.

A kutatóhely rövid bemutatása

Kutatásomat a Budapesti Műszaki és Gazdaságtudományi Egyetem Gép- és Terméktervezés Tanszékén végzem, amely az egyetem egyik legnagyobb tanszéke, és jelentős részt vállal a jövő gépészmérnökeinek oktatásában mind BSc. mind MSc. szinten. Az oktatás mellett a tanszéken több kutatási projekt is folyik, melyek témája többek között egyedi gépek tervezése, fejlesztése, valamint különböző folyamatok numerikus véges- és diszkrét elemes szimulációja.

A kutatás történetének, tágabb kontextusának bemutatása

A mezőgazdasági futóművek talajra gyakorolt hatásának vizsgálata az elmúlt század közepén kezdődött, amelynek keretében több kutatóintézetben szántóföldi mérések segítségével elemezték a kölcsönhatást. A mérések kiértékelése során több elmélet is született a talaj kerék alatti deformációjának, a talajban ébredő feszültségek valamint a kerék gördülési ellenállásának leírására vonatkozóan. Kiemelkedő eredményeket külföldön McKyes publikált 1985-ben [5]. Természetesen itthon is folytak ezzel kapcsolatos kutatások, és a jelenséget befolyásoló mechanikai jellemzők összefoglalóan Sitkei György jegyzetében [11] olvashatóak. Ezen kísérletek legnagyobb hátránya a magas költség, amely a szántóföldi mérések szervezésénél, lebonyolításánál, egyedi mérőberendezések tervezésénél és gyártásánál jelentett problémát.

A XX. század közepétől azonban a számítástechnika fejlődésének köszönhetően numerikus eljárásokat fejleszthettek ki a kutatók. Ezek segítségével a valós berendezés legyártása nélkül vizsgálhatók különböző folyamatok, ami jelentős költségmegtakarítást eredményezhet. A numerikus eljárások közül a legismertebb a VégesElemes Modellezés (VEM), azonban a talajok szemcsés felépítése miatt célravezetőbb megoldás a Diszkrét Elemes Modellezés (DEM) használata. Ezt több elismert nemzetközi folyóiratcikk támasztja alá, amelyek a talaj vágásával [10] valamint a talaj‒művelőelem kölcsönhatás leírásával foglalkoznak [1, 12].

A kutatás célja, a megválaszolandó kérdések

Célom olyan diszkrét elemes talajmodell létrehozása, amellyel helyesen modellezhető merev kerék kohézív talajon történő gördülése, megérthető a talaj kerék alatti mozgása és becsülhető a kerék gördülési ellenállása. Ennek a modellnek lehetőség szerint helyesen kell viselkednie a kerékre ható függőleges és a vízszintes erők esetén is, valamint szükséges megvizsgálni, hogy a két terhelést együtt véve valós talajnak megfelelő talajdeformációkat kapunk-e eredményül. Ehhez szükség van a korábbi kutatásomban felhasznált un. Linear, Parallel Bond és Hertz-Mindlin with bonding [3, 6, 7, 9] típusú kapcsolati modellek mikro-paramétereinek megfelelő kalibrálására, valamint laboratóriumi mérések elvégzésére is. További célom megvizsgálni a modellhatár szimulációs eredményekre gyakorolt hatását, amelyről az eddigi kutatások [4, 8] nem tesznek említést.

Módszerek

A talajt az 1970-es években publikált Diszkrét Elemes Módszer [2] segítségével modellezem. Az eljárás lényege, hogy a modell sok önálló szemcséből, un. diszkrét elemből áll, amelyek között kapcsolatot a különböző kapcsolati modellek teremtenek. A kapcsolati modellek segítségével az elemek között erők, illetve speciális kapcsolati modell esetén nyomatékok is átadódhatnak az ütközések során, amelyek befolyásolják az egyes elemek mozgását. Kohéziós talajok modellezésére megfelelő lehetőség az un. Parallel Bond kapcsolati modell használata [9], amellyel helyesen modellezhető a talajszemcsék közötti folyadékhidak hatása.

Ahhoz, hogy a létrehozott talajmodell kohéziós talajnak megfelelően viselkedjen, a felhasznált kapcsolati modell paramétereinek kalibrálására van szükség. Hajtott kerék alatt a talaj egyszerre nyomó és nyíró igénybevételnek is ki van téve, tehát a modellezésnél nagy hangsúlyt kellett fektetnem arra, hogy az anyagmodell mind nyomó, mind pedig nyíró jellegű terhelésnél valós talajnak megfelelően viselkedjen. Ehhez meg kellett határozni a modellezni kívánt talaj teherbírását (pl. a CI index segítségével) valamint súrlódásos mechanikai jellemzőit (kohézió, belső súrlódási szög) is. A valós talajok fent említett 3 anyagjellemzőjének meghatározásához szántóföldi- és laboratóriumi mérésekre egyaránt szükség volt. A teherbírást az un. kúpos penetrométeres szántóföldi, a súrlódásos jellemzőket pedig a direkt nyíródobozos vizsgálatokkal lehetett kimérni. A célom az volt, hogy numerikus szimulációkkal modellezve a fenti két mérést, az elemek közötti kapcsolati paramétereknek megfelelő értéket állítsak be, tehát kalibrálni tudjam a kapcsolati paraméterek értékét a valós mérési eredményeknek megfelelően.

A kutatás következő lépésében szükség volt egy olyan mérésre, amellyel vizsgálható a talaj deformációja, a rajta gördülő kerék mozgásállapota, mérhető a kerék gördülési ellenállása. A Szent István Egyetem munkatársaival együttműködve kidolgozásra került egy mérőberendezés, amellyel a NAIK Mezőgazdasági Gépesítési Intézetben laboratóriumi körülmények között egy talajvályúban elvégezhetők a szükséges mérések. A mérőberendezést az alábbi ábra szemlélteti, amelynek gyártása jelenleg folyamatban van, így a mérések idén nyáron lesznek elvégezve. A mérési eredmények ismeretében lehetőség lesz a talaj-kerék szimulációk validálására mind tolt, mind pedig hajtott kerék esetén.

 

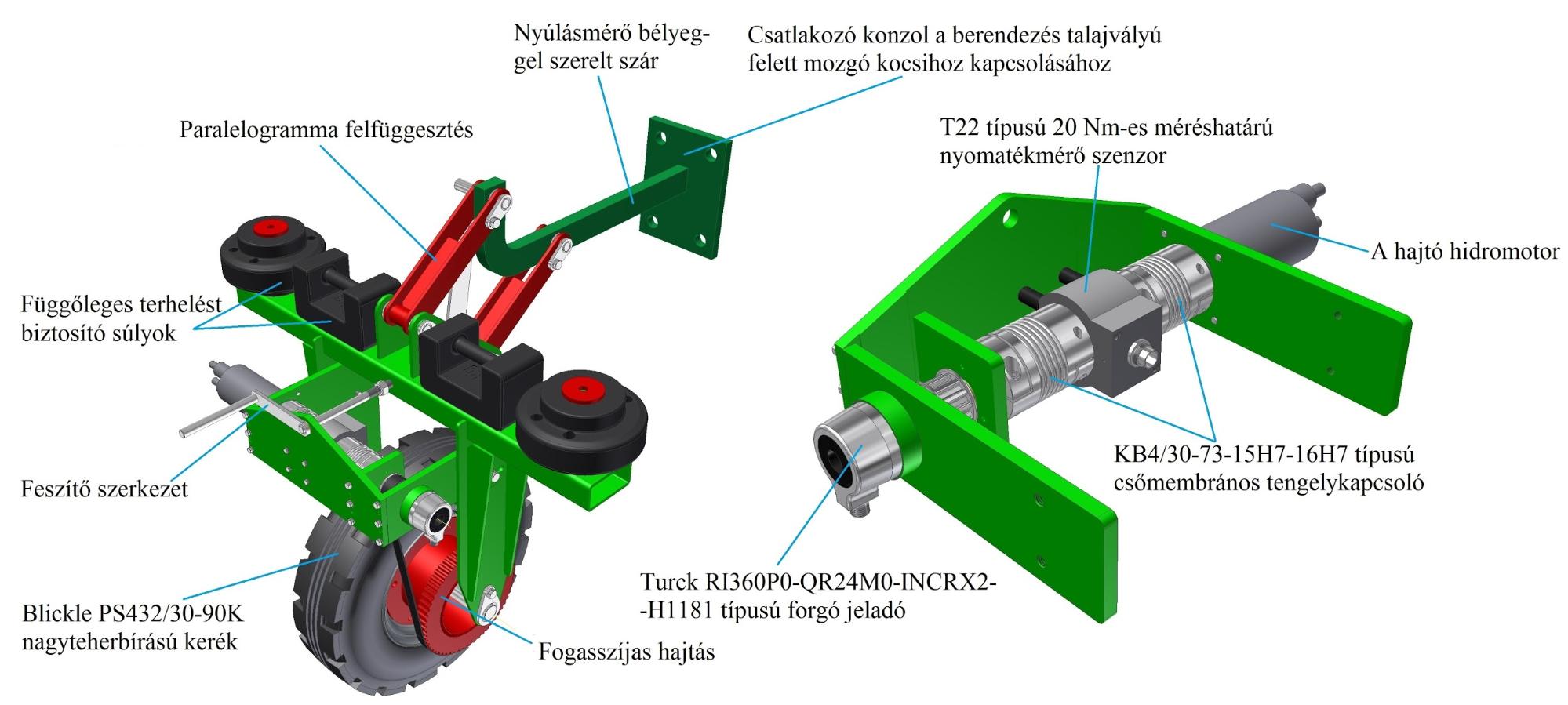
1. ábra. A talajvályús mérésekhez kidolgozott mérőberendezés terve.

Eddigi eredmények

A diszkrét elemes szimulációk során kohézív talaj modellezésére először a Particle Flow Code (PFC) szoftverben használható un. Linear súrlódásos és a Parallel Bond kapcsolati modelleket használtam fel. A kezdeti 2D-s szimulációk után 3D-s vizsgálatokat is végeztem direkt nyíródobozos, kúpos penetrométeres, továbbá merev kerék deformálódó talajon történő gördülésére vonatkozóan. Eredményeim közül kiemelném a kúpos penetrométeres szimulációknál a modellhatár változtatásának elemzését, amelynél négyzet és kör keresztmetszetű modellek esetén vizsgáltam a keresztmetszet nagyságának és a modell magasságának eredményekre gyakorolt hatását [K12]. Eredményeim alapján kijelenthető, hogy a keresztmetszet mérete jelentősen, míg a modell magassága csekély mértékben befolyásolja a talaj ellenállását (CI indexét). A következő ábrán látható a talajszemcsék elmozdulásának és sebességének alakulása a kúpos penetrométer talajba hatolásakor.

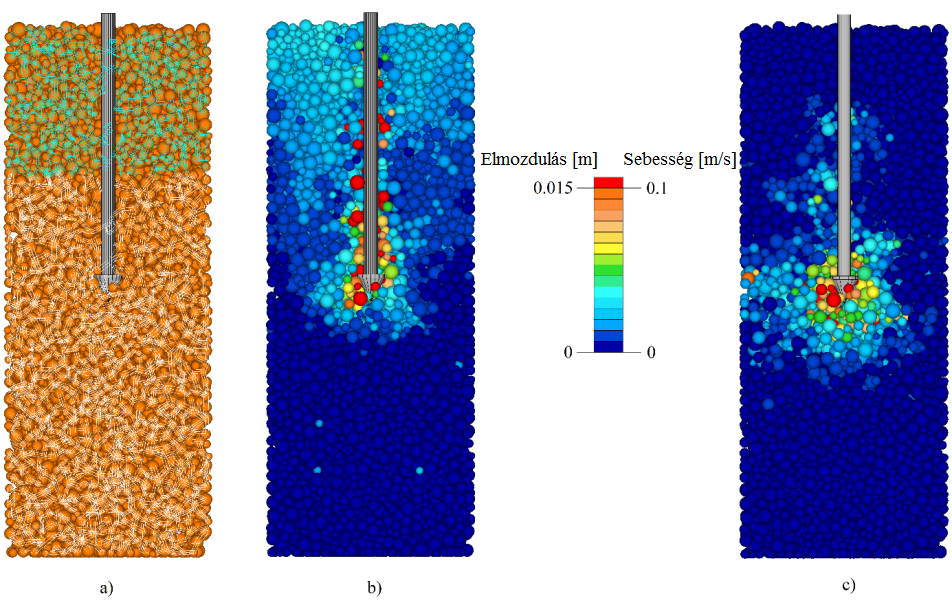
2. ábra. Pillanatképek kúpos penetrométeres szimulációkból: a) Diszkrét elemes talajmodell a Parallel Bond kapcsolatokkal; b) Elmozdulásmező; c) Sebességmező.

 

A direkt nyíródobozos szimulációkat a PFC szoftver mellett [K7; K8; K9] az EDEM diszkrét elemes szoftverben is elvégeztem [K13], amelyek esetén a Hertz-Mindlin with bonding típusú kapcsolati modellt használtam fel a talaj modellezésére. Ez a kapcsolati modell a nyomó és nyíró irányú mozgások leírásában tér el a fenti Linear modelltől, viszont kisebb számítási igénye van, ami miatt előnyösebb a használata. A direkt nyíródobozos szimulációk tekintetében megvizsgáltam, hogy az egyes kapcsolati paraméterek módszeres változtatása milyen hatással van a nyíróerő-elmozdulás görbére, ezáltal pedig a talaj kohéziójára és belső súrlódási szögére vonatkozóan. Eljárást dolgoztam ki a Hertz-Mindlin with bonding kapcsolati paraméterek kalibrálására, amellyel a valós nyíródobozos mérések eredményei és valós talaj súrlódásos mechanikai jellemzői (3. ábra) 5%-os hibahatáron belül kinyerhetők a szimulációkból [K13].

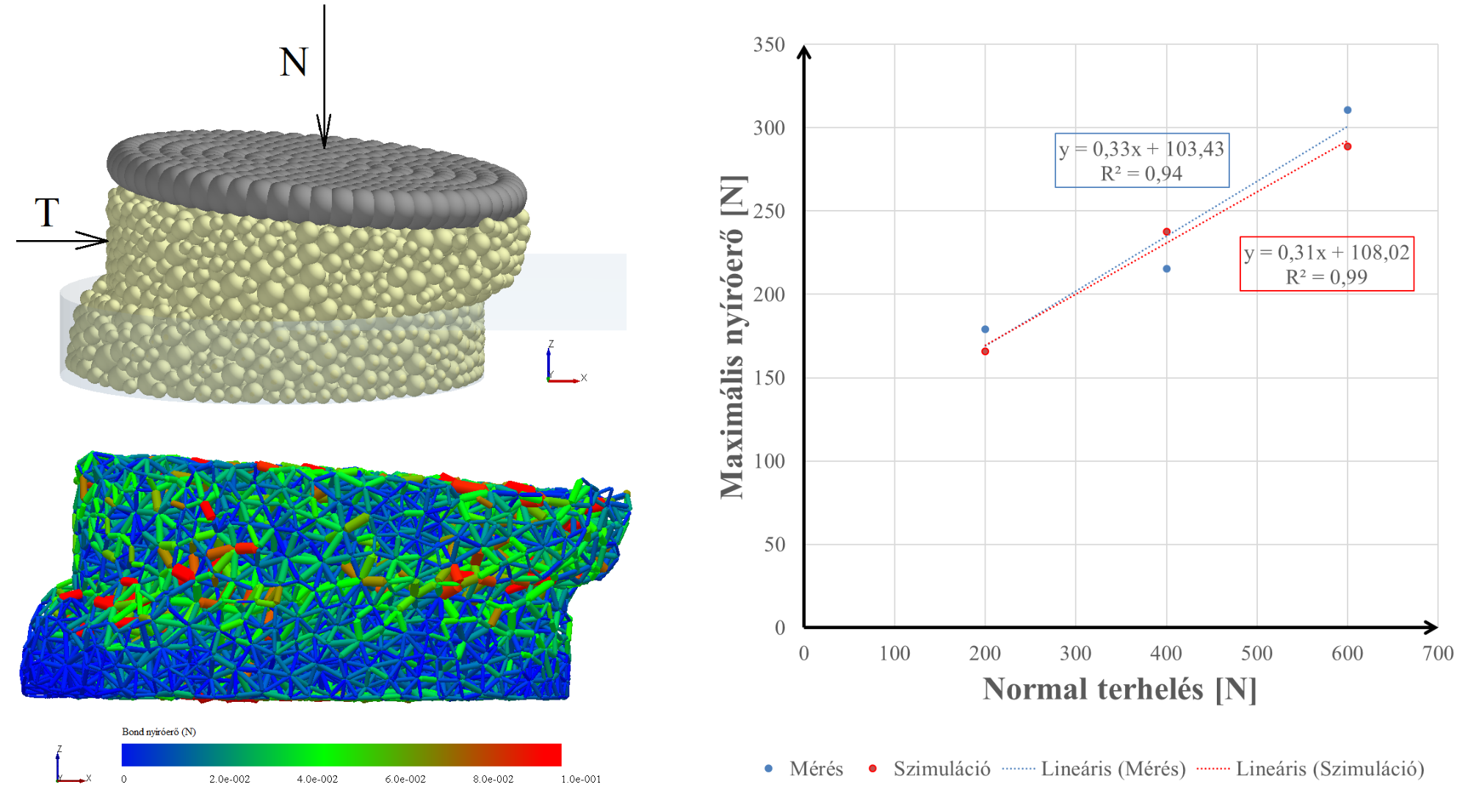
3. ábra. A nyíródobozos szimulációk eredménye.

A fentieken kívül vizsgáltam merev kerék statikus függőleges terhelés hatására bekövetkező talajba nyomódását [K7; K8; K9], valamint tolt kerék talajon gördülését [K10]. A kereket kétféle módszerrel, un. fal elemként valamint diszkrét elemként is modellezve vizsgáltam a kerék süllyedését, amely mindkét modellezési lehetőség esetén jól közelítette a Bekker-formulával számítható elméleti értéket (4. ábra).

 

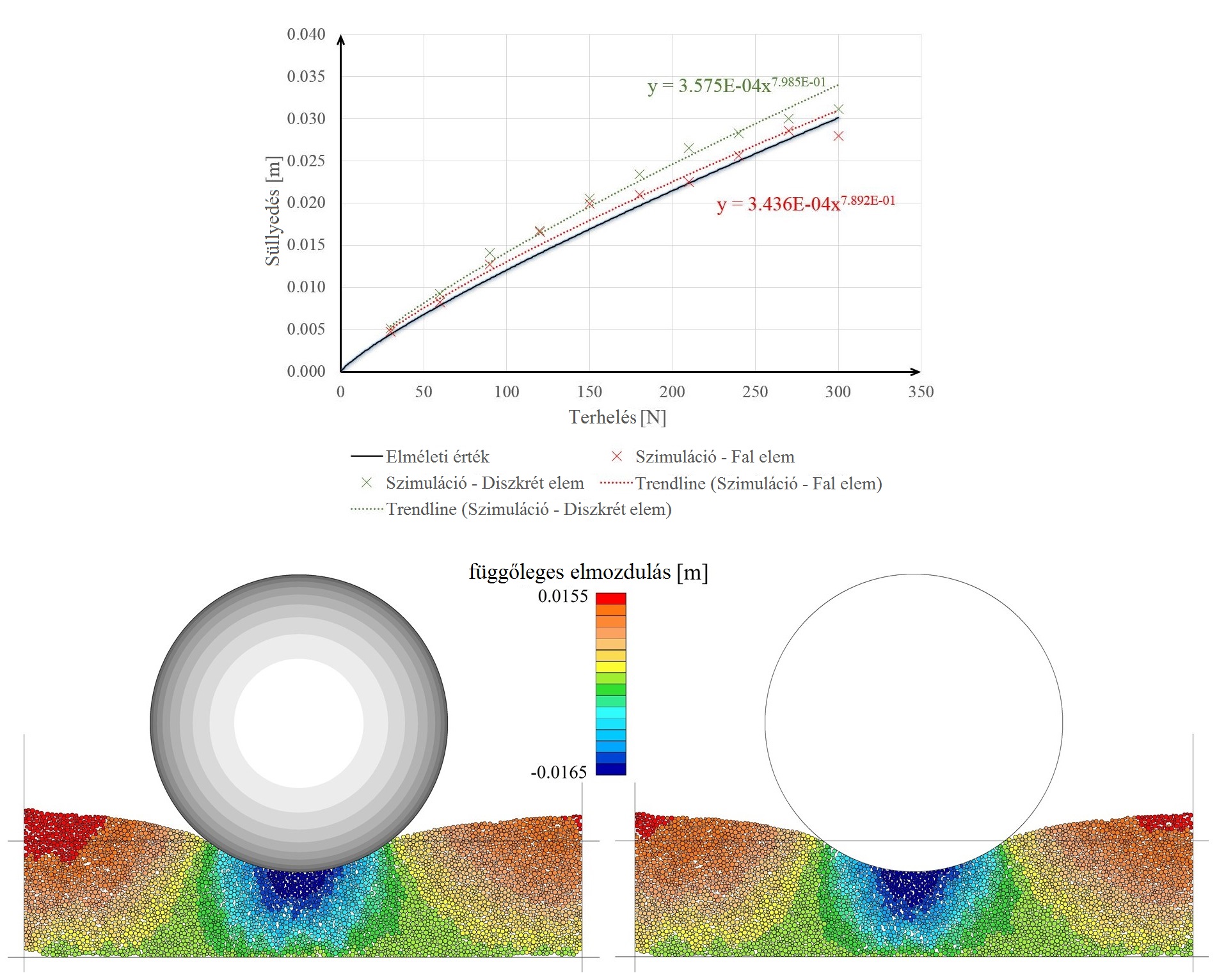
4. ábra. Álló kerék függőleges terhelés hatására bekövetkező süllyedése.

Jelenleg merev kerék deformálódó talajon való gördülésével foglalkozom, vizsgálataim tárgyát képezik a modellhatár hatásának vizsgálata. A szimulációk beállításai (a kerék geometriája, függőleges terhelése, sebessége, szlipje) minden paraméterben megegyeznek a nyár végén sorra kerülő talajvályús mérésekkel, így az eredmények ismeretében megtörténhet a számítások validálása is.

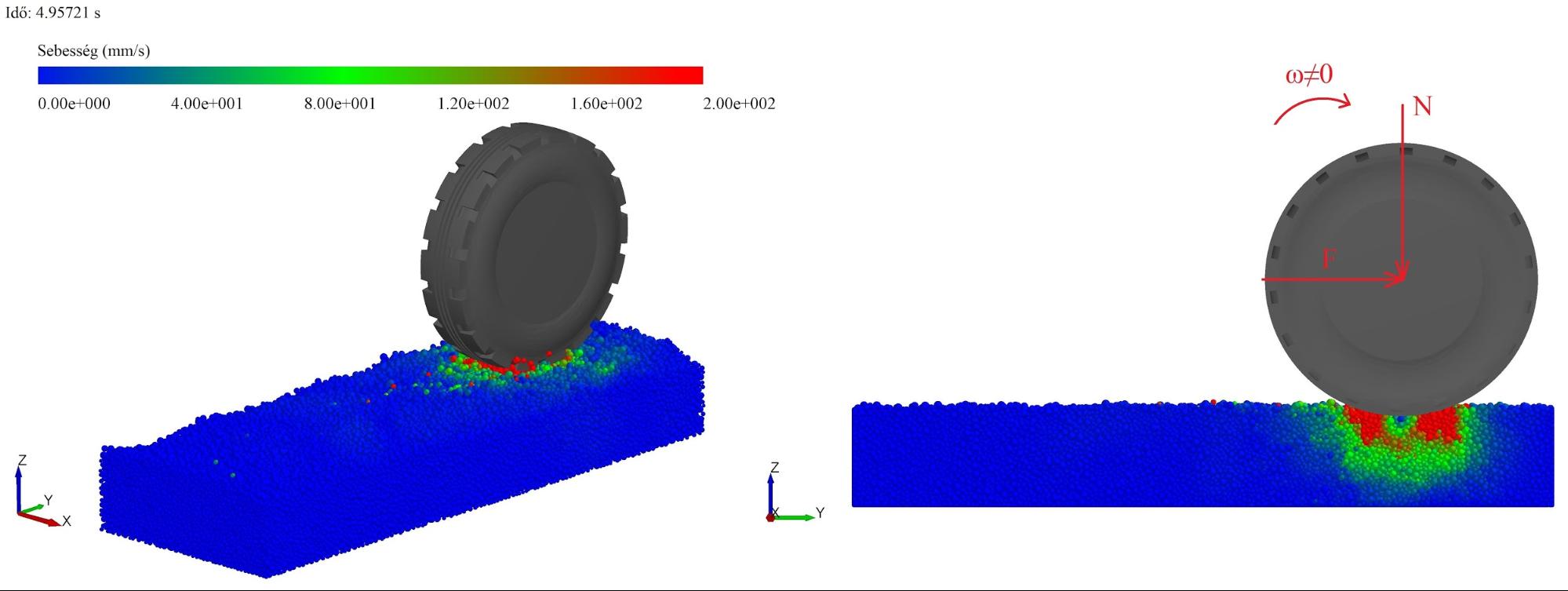
5. ábra. Tolt kerék-talaj kapcsolatának vizsgálata, a talajszemcsék elmozdulásmezője.

Várható impakt, további kutatás

Az elvégzett laboratóriumi mérések és a szimulációs eredmények összevetésével validálható az az eljárás, amelynek segítségével kerekek deformálódó talajon való gördülése modellezhető. A doktori disszertációmban ki fogok térni a diszkrét elemes modell határának vizsgálatára, továbbá javaslatot fogok tenni az elemek közötti kapcsolati paraméterek értékének beállítására úgy, hogy minőségileg és mennyiségileg helyesen deformálódó, a kerékre megfelelő mértékű ellenállást kifejtő talajmodellt kapjak eredményül. Ezzel lehetőség adódik a szántóföldi mérések részleges kiváltására, amely a futóművek és gumiabroncsok fejlesztésénél további költségcsökkentést eredményezhet.

Saját publikációk, hivatkozások, linkgyűjtemény

Kapcsolódó saját publikációk listája.

[K1] Rádics J. P., Kotrocz K., Modok K., Gyatyel Gy.: „Intelligens kompakt tárcsás borona fejlesztése.” GÉP XXVII., 2011/11. III. pp. 4-8.

[K2] Vidovics B., Rádics J. P., Jóri J. I., Kotrocz K., Lőrincz L.: „Mechanization challenge of harvesting arboreal energy plants.” Synergy & Technical Development: International Conference in Agricultural Engineering II. Gödöllő, Magyarország, 2011. okt. 9-15.
[K3] Kotrocz K., Kerényi Gy.: „Mezőgazdasági talajok szimulációja diszkrét elemes módszer segítségével.” GÉP XXVIII., 2012/12, pp. 65-68.
[K4] Földesi B., Rádics J. P., Kotrocz K., Tamás K., Jóri J. I.: „Diszkrét elemes anyagmodell paramétereinek meghatározása növényolajprés folyamatainak szimulációjához.” GÉP XXVIII., 2012/12, pp. 41-44.

[K5] Urbán M., Kotrocz K., Kerényi Gy.: „Investigation of the soil-tool interaction by SPH (Smooth Particle Hydrodynamics) based simulation.” International Conference of Agricultural Engineering, CIGR – AGENG. Valencia, Spanyolország, 2012. 2012. júl. 8-12.
[K6] Kotrocz K., Tamás K., Kerényi Gy.: „Discrete element method (DEM) modelling of cohesive soil-tool interaction.” Scientific Journal of Agricultural Engineering, Year XXXVIII, No.1, pp. 49-59, 2013.

[K7] Kotrocz K., Kerényi Gy.: „Investigation of soil rigid wheel contact under three different circumstances using discrete element method.” Mechanical Engineering Letters Volume 10, pp. 215-222, 2013.

Synergy & Technical Development: III. International Conference of CIGR Hungarian National Committee and Szent István University, Gödöllő, Magyarország, 2013. okt. 13-19.
[K8] Kotrocz K., Kerényi Gy.: „A talaj mechanikai jellemzőinek meghatározása talaj kerék kapcsolat szimulációjához DEM segítségével.” OGÉT XXI., Arad, Románia, pp. 201 204, 2013.
[K9] Kotrocz K., Kerényi Gy.: „Modeling of the soil-rigid wheel interaction using discrete element method.” Scientific Journal of Agricultural Engineering, Year XXXIX, No.3, pp. 1-11, 2014.

[K10] Kotrocz K., Kerényi Gy.: „Merev kerék deformálódó talajon történő mozgásának modellezése diszkrét elemes módszer segítségével.” OGÉT XXII., Nagyszeben, Románia, pp. 194-197, 2014.

[K11] Kovács Á., Kotrocz K., Kerényi Gy.: „The adaptability of discrete element method (DEM) in agricultural machine design.” Hungarian Agricultural Engineering (27) pp. 14-19, 2015.
[K12] Kotrocz K., Mouazen A. M., Kerényi Gy.: „Numerical simulation of soil cone penetrometer interaction using discrete element method. Computers and Electronics in Agriculture” 125:(C) pp. 63-73, 2016.

[K13] Kotrocz K., Kerényi Gy.: Numerical discrete element simulation of soil direct shear test. The 31st conference of the European Council for Modelling and Simulation Budapest, Magyarország, 2017. máj. 23-26.

 

Hivatkozások listája.

[1] Chen, Y., Munkholm, L. J., Nyord, T.: „A discrete element model for soil sweep interaction in three different soils.” Soil & Tillage Research, 126, 34-41, 2013.
[2] Cundall, P. A. and Strack, O. D. L.: “Discrete numerical model for granular assemblies.” Geotechnique, 29(1), 47-65, 1979.

[3] Hertz, H.: "On the contact of elastic solids." J. reine und angewandte Mathematik 92, 156-171, 1882.
[4] Knuth, M. A.; Johnson, J. B.; Hopkins, M. A.; Sullivan, R. J. and Moore, J. M.: “Discrete element modeling of a Mars Exploration Rover wheel in granular material.” Journal of Terramechanics, 49, 27-36, 2012.

[5] McKyes, E.: „Soil Cutting and Tillage.” Elsevier, New York, USA, 1985.
[6] Mindlin, R. D.: "Compliance of elastic bodies in contact." Journal of Applied Mechanics 16, 259-268, 1949.

[7] Mindlin, R. D. and Deresiewicz H.: "Elastic spheres in contact under varying oblique forces." ASME, September, 327-344, 1953.

[8] Nakashima, H.; Fujii, H.; Oida, A.; Momozu, M.; Kanamori, H.; Aoki, S.; Yokoyama, T.; Shimizu, H.; Miyasaka, J. and Ohdoi, K.: “Discrete element method analysis of single wheel performance for a small lunar rover on sloped terrain.” Journal of Terramechanics, 47, 307-321, 2010.

[9] Potyondy, D. O.; Cundall, P. A.: “A bonded-particle model for rock”. International Journal of Rock Mechanics & Mining Sciences, 41, 1329-1364, 2004.
[10] Shmulevich, I., Asaf, Z., Rubinstein, D.: "Interaction between soil and a wide cutting blade using the discrete element method.” Soil & Tillage Research, 97, 37-50, 2007.
[11] Sitkei, Gy.: „A mezőgazdasági gépek talajmechanikai problémái.” Akadémiai Kiadó, Budapest, 1967.

[12] Tamás, K., Jóri, J. I., Mouazen, A. M.: „Modelling soil-sweep interaction with discrete element method.” Soil & Tillage Research, 134, 223-231, 2013.