Géza Pattantyús-Ábrahám Doctoral School of Mechanical Engineering 

BME Gépészmérnöki Kar, Gép- és Terméktervezés Tanszék

Supervisor: Dr. Kerényi György

Discrete Element Modeling of Soil to Investigate the Soil-Wheel Interaction

Introducing the research area

This research focuses on the modeling of cohesive soils analyzing the soil-wheel interaction, primarily examining the possibility of numerical modeling of the effect of the wheel on the soil. In agricultural production, soil-wheel interaction is a frequently occurring phenomena, because the agricultural tractors exert their traction force through their wheels, while generating normal- and shear stress in the soil as well. Additionally to tractors, most agricultural machines is equipped with wheeled suspension which also pressurize the top layer of the soil.

In the past decades, the weight of agricultural machines has increased, increasing the load applied to the soil in vertical and horizontal directions as well. This contradicts to the expectations of environmentally-friendly, soil-friendly agricultural tillage, therefore, this phenomenon needs to be investigated.

Brief introduction of the research place

My research work is conducted at the Department of Machine and Product Design, one of the largest departments at the Budapest University of Technology. It undertakes a significant part in the education of BSc. and MSc. mechanical engineer students. Additionally to teaching, currently there are several research projects in progress at the department, including the design and development of special machines and numerical finite- and discrete element simulation of various processes.

History and context of the research

The investigation of the effect of agricultural suspensions on soil started in the middle of the last century. This interaction was analyzed by field measurements in several research institutes. Based on these tests, various theories were constructed to describe the deformation and stress generated in the soil under the loaded wheel and also the rolling resistance of the wheel. Outstanding results were published abroad in 1985 by McKyes [5]. Researches started in Hungary as well, and the mechanical properties of soils which affect this phenomenon were summarized by Sitkei [11]. However, these field measurements feature high cost of organizing, conducting the test, designing and manufacturing special measuring devices.

Throughout the past 60 years information technology has enormously evolved and various numerical methods have been developed by researchers. Using these methods the processes can be simulated without manufacturing the measuring devices, which reduces cost of experiments significantly. The best known method is the Finite Element Method (FEM), but because of the discrete structure of the soils, it is preferable to use the Discrete Element Method (DEM) for this phenomenon. This is supported by several well-known international journals that deal with soil cutting [10] and the description of the soil-sweep interaction [1, 12].

The research goal, open questions

My goals are to develop a discrete element soil model for the simulation of the rolling of a rigid wheel on cohesive soil; the deformation of the soil under the wheel can be analyzed; and the rolling resistance of the wheel can be estimated. The model should be capable of accurately simulating the soil under vertical and horizontal loads. In addition, it should be verified that model provides real soil deformations even if we apply vertical and horizontal load jointly (simultaneously). Therefore, it is necessary to calibrate the properties of the Linear, Parallel Bond and the Hertz-Mindlin with bonding type contact models [3, 6, 7, 9] and to conduct laboratory tests. Another goal is to investigate the effect of model boundary on the simulation results, a problem that has not been dealt with in previous researches [4, 8].

Methods

The soil is simulated using the Discrete Element Method [2] published in the 1970s. In this method, the model consists of a lot of individual particles, the so-called discrete elements which become into contact with each other by the contact models. Using these contact models forces and torques can be transmitted from one particle to another while they conflict with each other. These forces and moments affects the movement of the elements during the simulations. To model cohesive soils and the effect of the liquid bridge between the soil particles, the Parallel Bond contact model [9] can be a correct choice.

The first step of the modeling is the so called calibration process. In case of driven wheels, the soil is under normal and shear loads as well, therefore the developed soil model should behave similarly to real soil in case of normal and  shear load as well. Thus the bearing capacity (namely, the CI index) and the frictional mechanical properties of the soil (more closely, the cohesion and the internal frictional angle) have to be determined. To measure these properties laboratory and field tests have to be conducted; the bearing capacity of the soil can be determined by cone penetrometers in the field; the frictional properties can be determined by direct shear laboratory tests. My goal was to simulate these tests using numerical calculations, and to calibrate the contact properties according to the results of real measurements.

The next step was to conduct laboratory measurement to measure the deformation of the soil, the state of motion and the rolling resistance of the wheel. Therefore, a measuring equipment was designed jointly with the NARIC Institute of Agricultural Engineering to measure these quantities in soil-bin. This device is illustrated in Figure 1, the manufacturing process currently is in progress, so the measurements will be conducted this summer. The measurement results allow the validation of the soil-wheel simulations in case of driven and non-driven wheels as well.

 

 

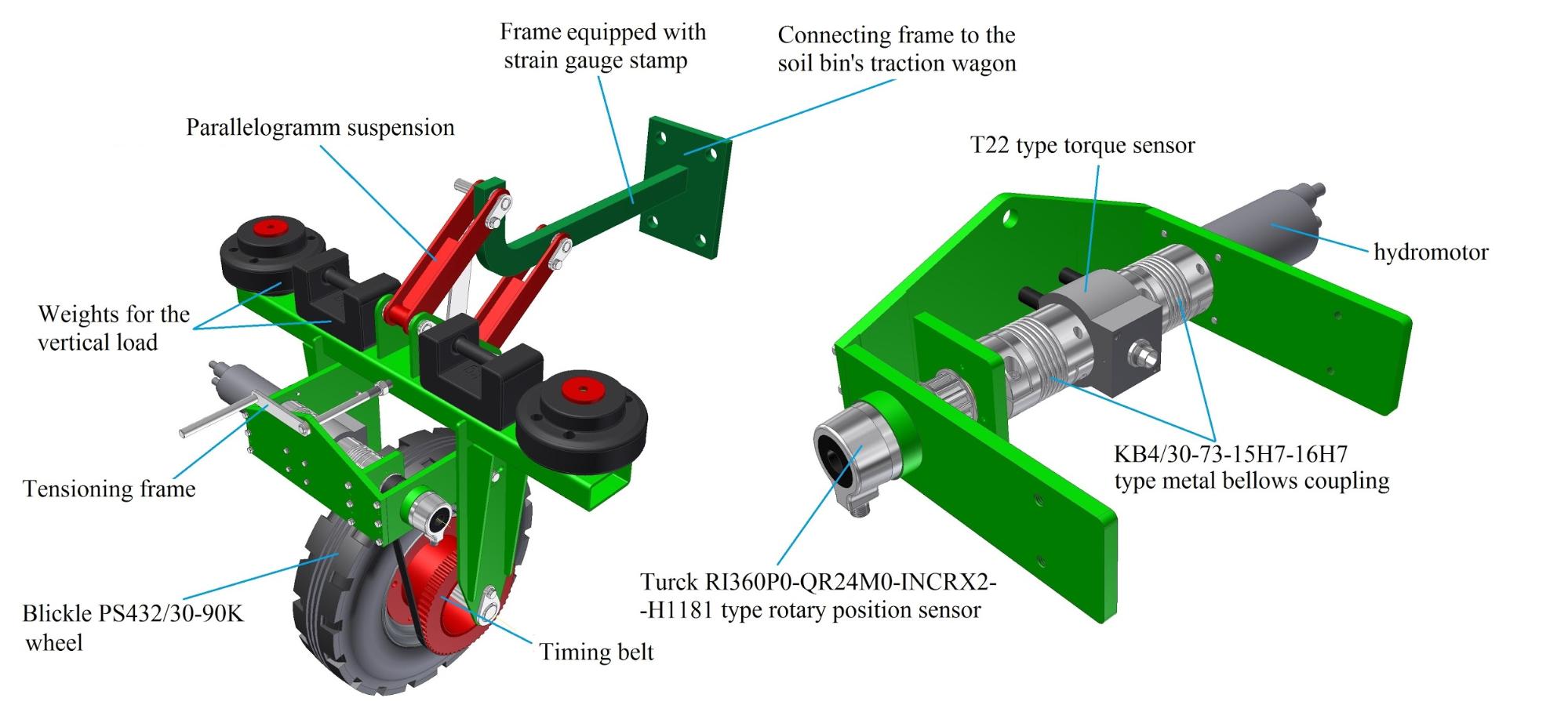
Figure 1. The concept of the measurement device for the soil-bin test.

Results

During the research process, to simulate cohesive soil the so-called Linear frictional and the Parallel Bond contact model were used in the Particle Flow Code (PFC) software. At first 2D and later 3D models were created to simulate soil direct shear, cone penetrometer tests and the rolling of a rigid wheel on deformable soil. From the results, I would like to highlight the analysis of the model boundary change where the effect of the size of the model’s cross section and the effect of the model’s height on the simulation results were investigated in case of soil model with rectangular and circular cross section as well [K12]. Results show that the cross section value has significant effect, and the height of the soil model has negligible influence on soil penetration resistance (CI index). In the following figure the displacement and the velocity of the soil particles were illustrated during the penetration process.

 

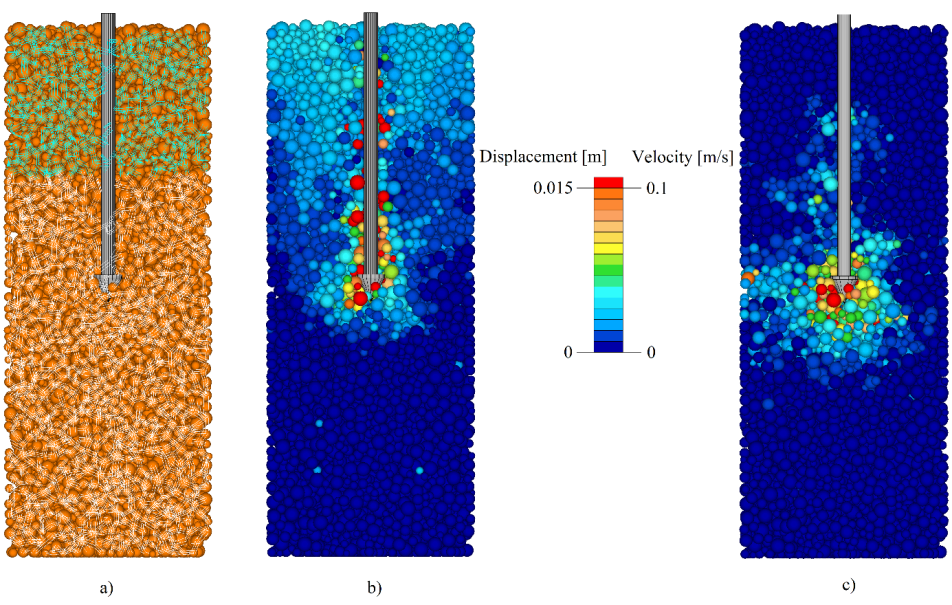
Figure 2. Screenshots from the cone penetrometer simulations: a) The discrete element soil model with the Parallel Bond contacts; b) Displacement field; c) Velocity field.

The numerical direct shear test were performed both in the PFC [K7; K8; K9] and in the EDEM software [K13] as well. Simulations in EDEM used the Hertz-Mindlin with bonding contact model which is different from the Linear model in describing the motion in normal and shear directions. Using this contact model the simulation takes less time to perform. In case of direct shear box simulations the effect of the contact properties on shear force-shear directions curve and therefore on soil’s cohesion and internal friction angle was investigated individually. A method was developed to calibrate the contact parameters of the Hertz-Mindlin with bonding model and to get results with relative error below 5% in the soil’s frictional mechanical properties (see Figure 3) while comparing the data to the results of real direct shear tests.

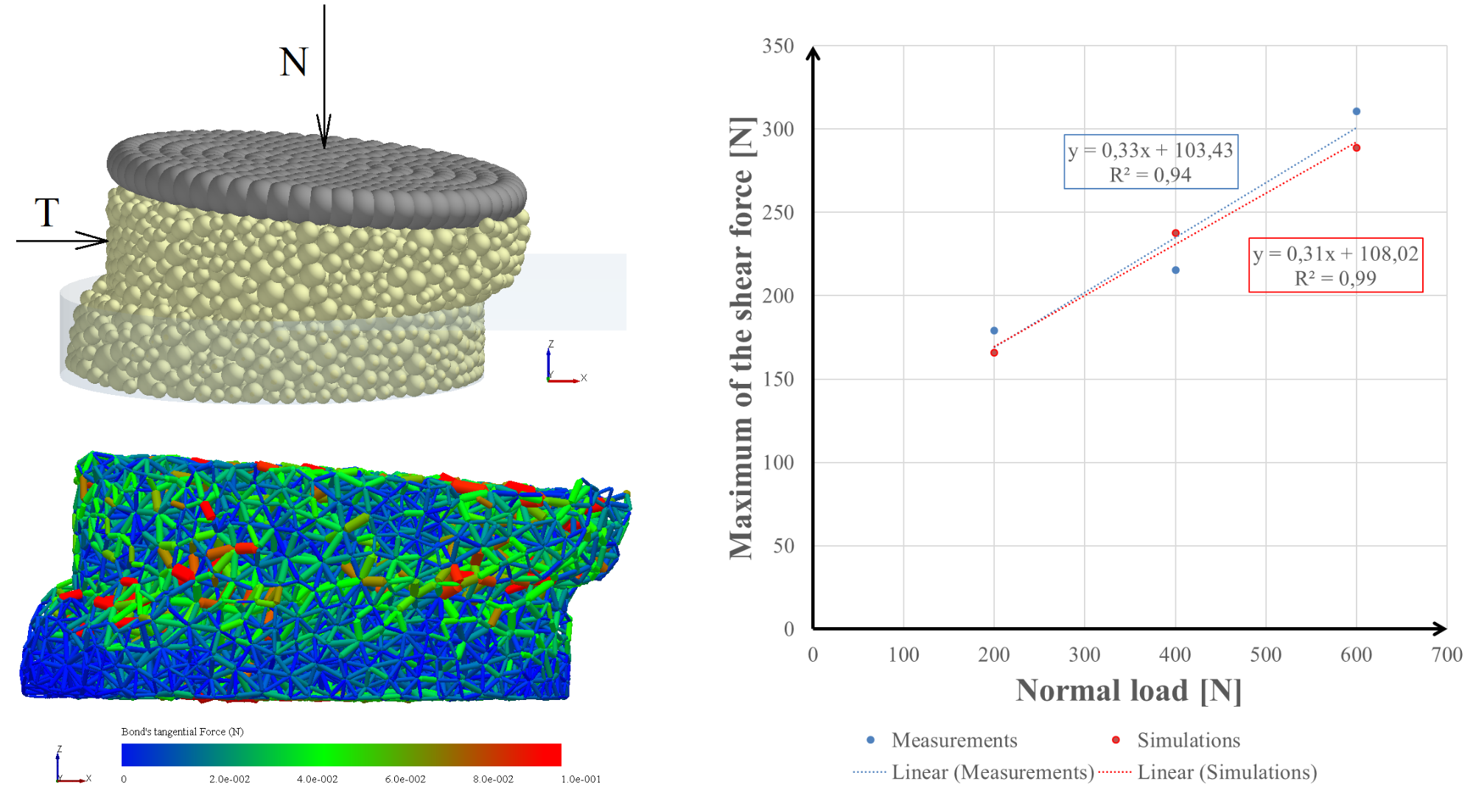
Figure 3. The results of numerical direct shear tests.

In addition the sinkage of the rigid wheel under vertical load [K7; K8; K9] and the rolling of the wheel was investigated [K10]. The wheel was modeled by two different ways, first as a wall-element and then as a discrete element. Both ways resulted similar results which are in good agreement with the theoretical sinkage values from the Bekker-formulae (see Figure 4.).

Figure 4. The sinkage of the rigid wheel under vertical load.

Currently, the investigation of the model’s boundary for rigid wheels rolling on deformable soil is in progress. The settings of the simulations (namely geometry, vertical load, the velocity and the slip of the wheel) all agree with the settings of the soil-bin laboratory test to be conducted this summer. Therefore, the simulation can be validated based on these results. A screenshot from these simulations can be seen in Figure 5.

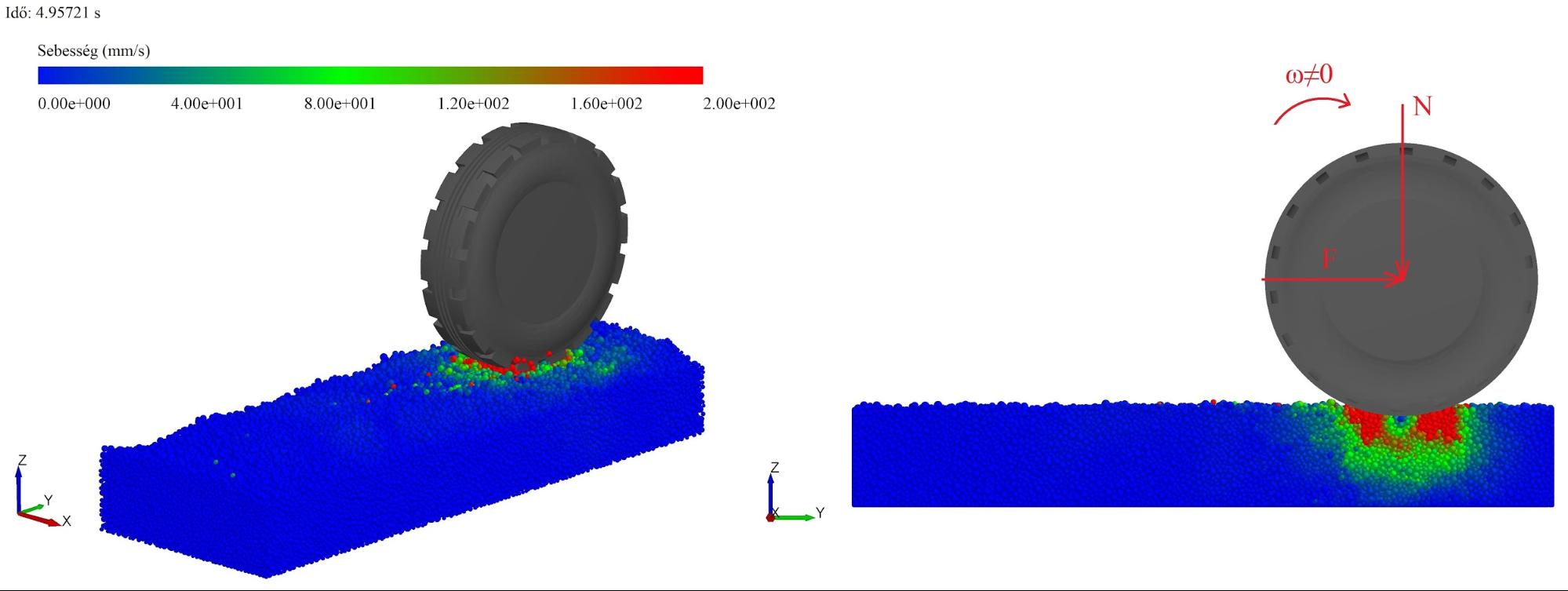
Figure 5. Non-driven wheel-soil interaction, the displacement of soil particles.

Expected impacts and further research

The modelling method to simulate the rolling of the wheel on deformable soil can be validated by comparing the results of the laboratory tests and the calculations. In my thesis I will deal with the investigations of the effect of model boundary and I will propose the setting of the contact properties so that the correct results in soil deformation and a soil model with correct resistance on the wheel can be obtained.

Publications, references, links

Own publications

[K1] Rádics J. P., Kotrocz K., Modok K., Gyatyel Gy.: ”Intelligens kompakt tárcsás borona fejlesztése.” (in Hungarian) GÉP XXVII., 2011/11. III. pp. 4-8.
[K2] Vidovics B., Rádics J. P., Jóri J. I., Kotrocz K., Lőrincz L.: “Mechanization challenge of harvesting arboreal energy plants.” (in Hungarian) Synergy & Technical Development: International Conference in Agricultural Engineering II. Gödöllő, Hungary, 9-15 October, 2011.
[K3] Kotrocz K., Kerényi Gy.: “Mezőgazdasági talajok szimulációja diszkrét elemes módszer segítségével.” (in Hungarian) GÉP XXVIII., 2012/12, pp. 65-68.
[K4] Földesi B., Rádics J. P., Kotrocz K., Tamás K., Jóri J. I.: „Diszkrét elemes anyagmodell paramétereinek meghatározása növényolajprés folyamatainak szimulációjához.” (in Hungarian) GÉP XXVIII., 2012/12, pp. 41-44.
[K5] Urbán M., Kotrocz K., Kerényi Gy.: “Investigation of the soil-tool interaction by SPH (Smooth Particle Hydrodynamics) based simulation.” International Conference of Agricultural Engineering, CIGR – AGENG. Valencia, Spain, 2012. 8–12 June, 2012
[K6] Kotrocz K., Tamás K., Kerényi Gy.: “Discrete element method (DEM) modelling of cohesive soil-tool interaction.” Scientific Journal of Agricultural Engineering, Year XXXVIII, No.1, pp. 49-59, 2013.

[K7] Kotrocz K., Kerényi Gy.: “Investigation of soil rigid wheel contact under three different circumstances using discrete element method.” Mechanical Engineering Letters Volume 10, pp. 215-222, 2013.

Synergy & Technical Development: III. International Conference of CIGR Hungarian National Committee and Szent István University, Gödöllő, Hungary, 13–19 October, 2013
[K8] Kotrocz K., Kerényi Gy.: “A talaj mechanikai jellemzőinek meghatározása talaj kerék kapcsolat szimulációjához DEM segítségével.” (in Hungarian) OGÉT XXI., Arad, Romania, pp. 201 204, 2013

[K9] Kotrocz K., Kerényi Gy.: “Modeling of the soil-rigid wheel interaction using discrete element method.” Scientific Journal of Agricultural Engineering, Year XXXIX, No.3, pp. 1-11, 2014.

[K10] Kotrocz K., Kerényi Gy.: “Merev kerék deformálódó talajon történő mozgásának modellezése diszkrét elemes módszer segítségével.” (in Hungarian) OGÉT XXII., Nagyszeben, Romania, pp. 194-197, 2014.

[K11] Kovács Á., Kotrocz K., Kerényi Gy.: “The adaptability of discrete element method (DEM) in agricultural machine design.” Hungarian Agricultural Engineering (27) pp. 14–19, 2015.
[K12] Kotrocz K., Mouazen A. M., Kerényi Gy.: “Numerical simulation of soil cone penetrometer interaction using discrete element method. Computers and Electronics in Agriculture” 125:(C) pp. 63–73, 2016.

[K13] Kotrocz K., Kerényi Gy.: Numerical discrete element simulation of soil direct shear test. The 31st Conference of the European Council for Modelling and Simulation Budapest, Hungary, 23–26 May, 2017

 

References.

[1] Chen, Y., Munkholm, L. J., Nyord, T.: “A discrete element model for soil sweep interaction in three different soils.” Soil & Tillage Research, 126, 34–41, 2013.
[2] Cundall, P. A. and Strack, O. D. L.: “Discrete numerical model for granular assemblies.” Geotechnique, 29(1), 47-65, 1979.

[3] Hertz, H.: "On the contact of elastic solids." J. reine und angewandte Mathematik 92, 156–171, 1882.

[4] Knuth, M. A.; Johnson, J. B.; Hopkins, M. A.; Sullivan, R. J. and Moore, J. M.: “Discrete element modeling of a Mars Exploration Rover wheel in granular material.” Journal of Terramechanics, 49, 27–36, 2012.

[5] McKyes, E.: “Soil Cutting and Tillage.” Elsevier, New York, USA, 1985.
[6] Mindlin, R. D.: "Compliance of elastic bodies in contact." Journal of Applied Mechanics 16, 259-268, 1949.

[7] Mindlin, R. D. and Deresiewicz H.: "Elastic spheres in contact under varying oblique forces." ASME, September, 327-344, 1953.

[8] Nakashima, H.; Fujii, H.; Oida, A.; Momozu, M.; Kanamori, H.; Aoki, S.; Yokoyama, T.; Shimizu, H.; Miyasaka, J. and Ohdoi, K.: “Discrete element method analysis of single wheel performance for a small lunar rover on sloped terrain.” Journal of Terramechanics, 47, 307–321, 2010.

[9] Potyondy, D. O.; Cundall, P. A.: “A bonded-particle model for rock”. International Journal of Rock Mechanics & Mining Sciences, 41, 1329–1364, 2004.
[10] Shmulevich, I., Asaf, Z., Rubinstein, D.: "Interaction between soil and a wide cutting blade using the discrete element method.” Soil & Tillage Research, 97, 37–50, 2007.
[11] Sitkei, Gy.: „A mezőgazdasági gépek talajmechanikai problémái.” (in Hungarian) Akadémiai Kiadó, Budapest, 1967.

[12] Tamás, K., Jóri, J. I., Mouazen, A. M.: “Modelling soil-sweep interaction with discrete element method.” Soil & Tillage Research, 134, 223–231, 2013.