|
|
BMe Kutatói pályázat |
|
Vásárhelyi Pál Építőmérnöki és Földtudományok Doktori Iskola
BME ÉPK, Tartószerkezetek Mechanikája Tanszék
Témavezető: Dr. Bojtár Imre
Értágulatok kialakulásának és felhasadásának mechanikája
A kutatási téma néhány soros bemutatása
Kutatásom témája az emberi érhálózat kóros tágulatainak (aneurizmák) biomechanikai vizsgálata. Az elváltozások fő előfordulási helyei az agyi érhálózat elágazási pontjai és a szívből kiinduló főverőér hasi része. Kezelésük kockázatos, esetleges felhasadásuk pedig a nyugati társadalom egyik leggyakoribb halálozási okai közé tartozik. A modern képalkotó eljárások és a gyakori szűrővizsgálatok megteremtették a lehetőségét, hogy ezt a populáció jelentős hányadában jelen lévő és egyébként tünetmentes elváltozást akár egy mellkasröntgen vagy ultrahang vizsgálat során is a kritikusnál korábbi fázisban észrevegyük, azonban mind kialakulásuk, mind a hirtelen bekövetkező megrepedésük okai ismeretlenek, így a klinikai gyakorlat a kezelést illető döntések során csak statisztikai adatokra támaszkodhat. Az általam kidolgozott eljárás megteremti a lehetőségét többek között a betegre szabott, gyors és beavatkozásmentes felhasadási kockázat elemzésre, segítve a műtéti rangsor felállítását és a kezelés módjának biomechanikailag megalapozott megválasztását.
A kutatóhely rövid bemutatása
Kutatásaimat az Építőmérnöki Kar egyik legaktívabb, nemzetközi szintű kutatási munkát végző részlegén, a Tartószerkezetek Mechanikája Tanszékén folytatom. Itt több futó OTKA keretében a mechanikai alapkutatások, a szerkezeti optimalizálás és az innovatív szakmai fejlesztések mellett jelentős szerepet kap a biomechanika problémákra irányuló, kísérletekkel és numerikus szimulációkkal alátámasztott megoldások kidolgozása gyakorló orvosokkal szorosan együttműködve. Esetemben ez a Semmelweis Egyetem Klinikai Kísérleti Kutató- és Humán Élettani Intézetét, a Biofizikai és Sugárbiológiai Intézetét, a Városmajori Szív és Érsebészeti Klinikát és a University of Texas San Antonio Vascular Biomechanics and Biofluids Laboratory-ját jelenti. Témavezetőm, Bojtár Imre a magyar biomechanikai kutatások szervező úttörője, a Biomechanikai Kooperációs Kutatóközpont alapító igazgatója.
A kutatás történetének, tágabb kontextusának bemutatása
Az értágulatok felhasadása lokális probléma, és összetett biomechanikai tényezők okozzák. Tisztán mechanikai megközelítésben akkor következik be, ha a véráram terhelő hatása által a falban kialakuló igénybevételek meghaladják annak teherbírási határértékét.
Az elv legegyszerűbb következménye a klinikum ökölszabályának kvalitatív igazolása a görbült membránokra érvényes Laplace-törvénnyel, mely szerint a hasi tágulat [H1] átmérőjének növekedtével nő a felhasadás kockázata. 5,5 cm az a tapasztalati határ [H2, H3], ami felett már a felhasadás statisztikai veszélye nagyobb, mint a sebészeti beavatkozás kockázata [H4].
Valós esetekben viszont az ennél kisebb tágulatok is rupturálnak [H5], vagyis a komplex peremfeltételek, a geometria, az időben változó viselkedés és a lokálisan jelentős eltéréseket mutató anyagtulajdonságok következtében nem juthatunk ilyen egyszerűen megfogalmazott, analitikusan levezethető megállapításokhoz, ezért a mérnöki gyakorlat numerikus szimulációs technikái felé fordult a tudományterület, melynek mai állása szerint a szilárd és a folyadék fázis kölcsönös egymásra hatását figyelembe vevő végeselemes (FE) eljárást és véges térfogatok módszerét (FVM) kapcsoló FSI technikával kereskedelmi szoftverekkel elvi lehetőség adódik a falfeszültségek páciens-specifikus meghatározására [H6, H7].
Az eljárás azonban túlzottan szakértelem-, erőforrás- és időigényes a gyakorlatba való átültetéshez. Mindezek mellett használata erős kritikával illethető, mivel a biztonság kárára figyelmen kívül hagyja a tágulat megfigyelt ridegedése és merevebbé válása következtében fellépő tönkremeneteli kritériumbeli csökkenést, illetve a feszültségkoncentráló hatást. Mindezek fő oka - annak ellenére, hogy rendelkezésünkre áll egy adekvát, mikroszerkezeti alapon meghatározott anyagmodell [H8] - az élő szervezetben fennálló (in-vivo) anyagi paraméterek térbeli eloszlása ismeretének hiánya.
A kutatás célja, a megválaszolandó kérdések.
Célom egy olyan a gyakorlatban is alkalmazható, az orvoslásban már használatban lévő eszközöket felhasználó döntéssegítő módszer kifejlesztése és szoftveres implementációja, amely kijavítja a fent említett hiányosságokat.
Ennek fő modulja egy a végeselemes módszer új paradigmáján (IGA [H9]) alapuló gyors optimalizációs eljárás, amely során a mért alakváltozás- és tehermező közt kapcsolatot teremtő inhomogén anyagmodell beteg-specifikus paramétereinek lokális meghatározását végezzük el in-vivo, mely elengedhetetlen a valós feszültségeloszlás előállításához.
A módszert az adott páciens egészséges érszakaszaira is alkalmazva az időben hosszan elnyúló roncsolódás mértékét szintén egyénileg kalibráljuk és mérjük, mellyel in-vitro preparátumokon végzett mérések alapján az egyénre szabott tönkremeneteli feltétel is megadható, ezzel egy új, roncsolódási fokon alapuló felhasadási kritériumot is felállítottunk.
A módszer validálását nyílt sebészeti beavatkozáson átesett betegekből az operáció során kimetszett mintákon végezzük el. A mechanikai makrojellemzőket biaxiális húzókísérletekkel; a fal fő alkotóinak, a kollagénnek és az elasztinnak az elrendeződéséből adódó mikrostruktúrát pedig multifoton mikroszkópos felvételek és szövettani metszetek segítségével határozzuk meg. A téma interdiszciplinaritása megköveteli a tudományágak közti szoros együttműködést, a gyakorlati cél pedig a praktikummal való folytonos konzultációt, így munkánkban jelentős szerepet töltenek be a kutatóhely bemutatása során említett intézetek.
Módszerek
A kutatási folyamat az 1. ábrán látható öt fő részre bontható:
-
az alakváltozás-mezőt meghatározó,
-
a tehermezőt automatikusan szimuláló, és
-
az anyagi paraméterek optimalizációját végző algoritmus kifejlesztésére,
-
a kísérleti validációra, és
-
a roncsolódási fok meghatározására.
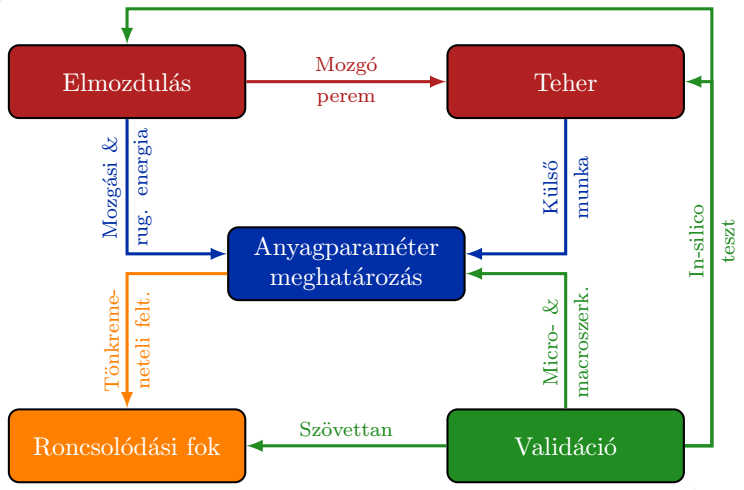
1. ábra: A kutatási folyamat lépéseinek folyamatábrája.
Alakváltozás-mező
Az Érsebészeti Klinikán elérhető, EKG-kapuzott CTA készítésére alkalmas Philips Brilliance iCT 256 berendezéssel az állandósult szívciklusok különböző diszkrét pillanataiban készítünk felvételeket a hasüregről, amelyben a megfestett véráram még elfogadható sugárdózis mellett is jó felbontású képet ad az áramlási térről (lumen), melynek pontjaival megadott alakját így időben követni tudjuk egy aktív kontúr alapú algoritmus segítségével. Ez szolgál bemenő adatként az alábbiakban részletezendő eljárásunkhoz [S1].
A felvételek mérési hibája a voxel méretével közelíthető, amely a felület mozgásához képest nem hanyagolható el. Ezek kiküszöbölésére térbeli és időbeli simítást alkalmaztam, majd a felületet térben és időben is analitikus függvénnyel adtam meg egy új és robusztus illesztőeljárással [S3].
A merevtest-szerű mozgások kiszűrése után a felületi pontok elmozdulásait határoztam meg. Az elve FSI szimulációk során tett megfigyeléseken alapszik, nevezetesen a felület függvényszerű megadása után azok pontjait időben megfelelően sűrítve a pillanatnyi normális irányban mozdítom el, majd a periodicitást biztosítandó, a pálya záródási hibáját lineárisan szétosztva korrigálom az elmozdulásokat.
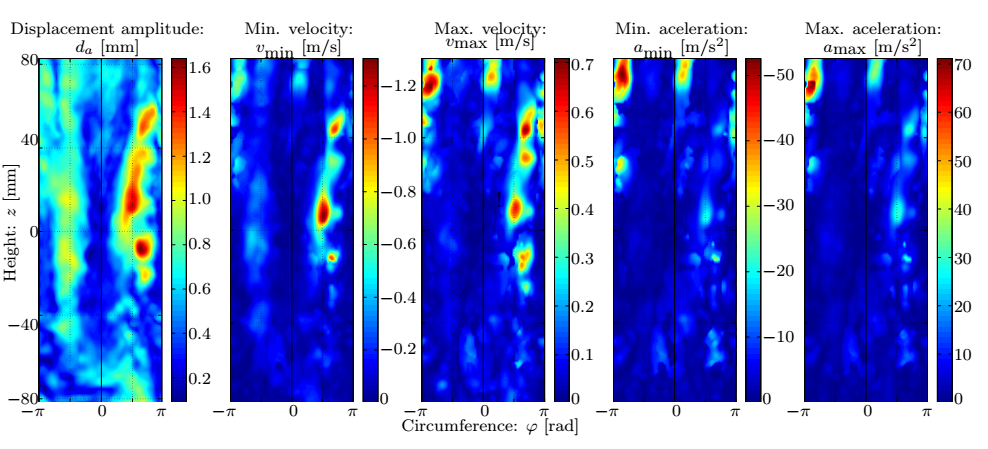
2. ábra: A referenciafelület kinematikai változóinak jellemző értékei [S2].
Az alakváltozások és alakváltozás-sebességek meghatározásához a héjelmélet és a végeselemes módszer eszköztárát alkalmaztam a Kirchhoff-Love-féle elmélet általánosításával, elvetve a referenciafelületre merőleges szálak összenyomhatatlanságának feltételezését.
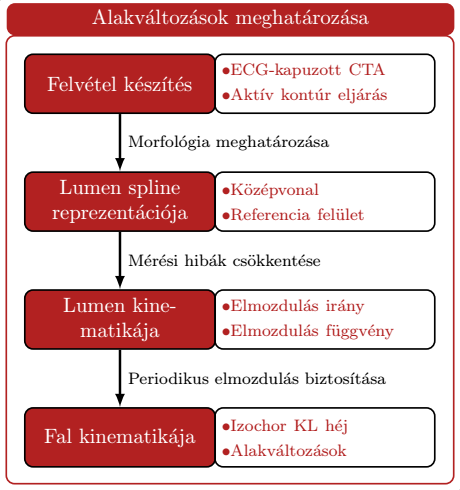
3. ábra: Az alakváltozás-mező meghatározásának lépései.
Tehermező
A folyadékáramlás szimulációjához bemenő adatként a végtagon vagy ritkább esetben szondával mért sebesség-idő és nyomás-idő függvény szükséges, mely egy egy-dimenziós modell segítségével a vizsgált érszakaszra transzformálható [H10]. Az időfüggő sebességprofil kialakulásához a belépő keresztmetszet előtt megfelelő hosszú fiktív csőszakasz szolgál. A követő érszakaszok viselkedését pedig a kilépő keresztmetszethez rögzített csőszakasz negatív tömeg és impulzusforrása modellezi. A legfontosabb újításunkkal és a fal mozgásainak ismeretével pedig a számításigényes kapcsolt FSI szimuláció elkerülhető, és a falra átadódó terhek gyorsan számíthatók.
Anyagi paraméterek
A diszkretizált mozgásegyenletek differenciális alakjában egyedül a merevségi mátrix függ az ismeretlen, de konstansnak feltételezett anyagi paraméterektől. A csillapítási mátrixot jelenleg elhagytam, a későbbiekben viszont Rayleigh-csillapítással tervezem figyelembe venni, amely paramétereit a szívciklus jól meghatározott frekvenciáján, valós mintákon végzett ciklikus mérésekből adódó energiadisszipációból kielégítően közelíthető. Az optimalizáció az elmozdulásokból számított és a szimulációból adódó csomóponti tehervektor különbségének normáját minimalizálja Levenberg-Marquardt algoritmus alapján az anyagi paraméterekre tett megfelelő megkötések mellett. Az eljárás rendkívül gyors, ugyanis a fenti megfogalmazás mellett nincs szükség a merevségi mátrix invertálására, és a végeselemes módszer előnyeit kihasználva a paramétertérben tett lépésirány számítási ideje is lecsökkenthető a függvény kiértékelését megközelítő értékre, így nem okoz problémát az 105 nagyságrendű ismeretlenszám sem.
Validáció
A kutatás befejező szakaszában az operáció során kivett mintákon egy órán belül elvégzett biaxiális húzóvizsgálatokkal, majd a későbbi szövettani és multifoton mikroszkópos felvételekkel validáljuk a modell által kapott eredményeket.
Eddigi eredmények
Az eljárás fenti öt alappilléréből az alakváltozás-mező számítása és az optimalizációs algoritmus elkészült [S1], a validációs folyamatot szilikon mintákon elvégeztük [S3], és a valós mintákhoz szükséges előkészületek is megtörténtek, a szükséges eszközök és körülmények rendelkezésünkre állnak. Jelenleg folyamatban van a részeredmények publikálása és az áramlástani modell automatizálása is.
In-vivo alakváltozás mérés
Jelenleg képesek vagyunk az alakváltozások automatizált, in-vivo meghatározására. Ehhez a 4. ábrán részletezett paraméter-tanulmányok során meghatároztam a simítófüggvény paramétereit: a két-dimenziós harmadfokú B-spline foltjainak méretét és az időbeli Fourier-transzformáció után a frekvenciatérben végrehajtott zajszűrés amplitúdó kritériumát, analitikus leírását adva ezzel az áramlási tér határfelületének.
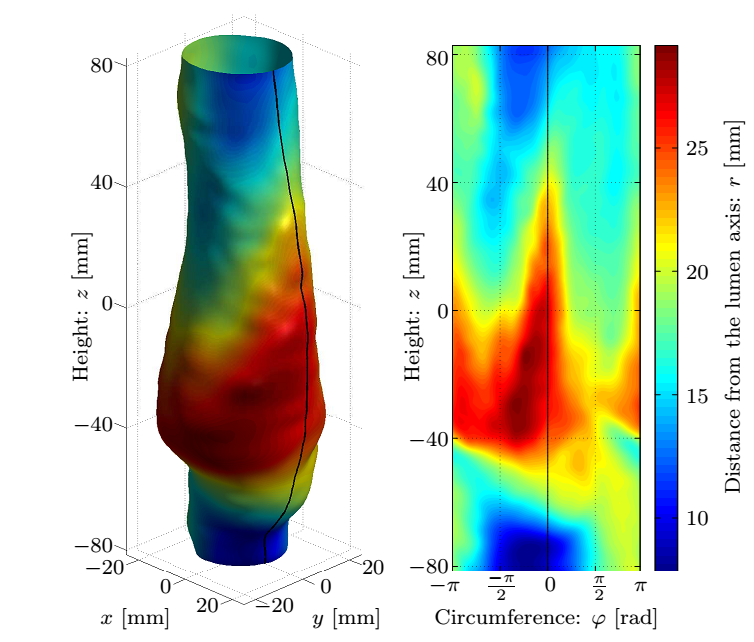
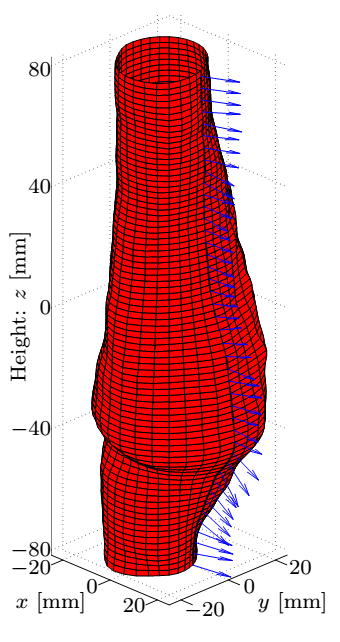
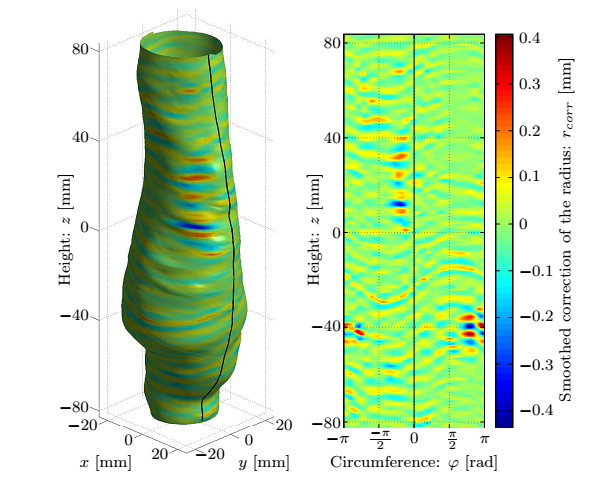
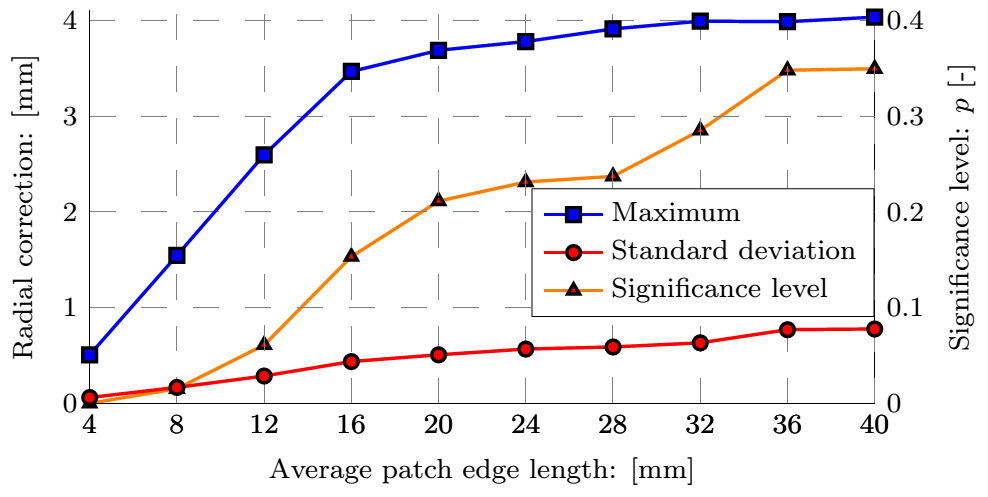
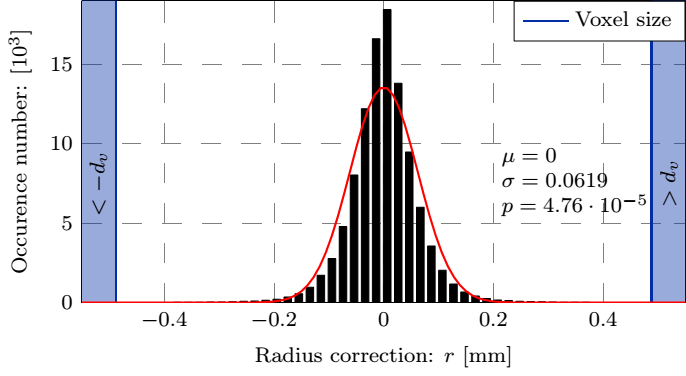
4. ábra: A felső sorban az aneurizma geometriája, a simított felület és a normálisok szemléltetése valamint a mért koordináták távolsága az illesztett felülettől. Az alsó sorban a B-spline foltok méretének függvényében a korrekció maximális és átlagos értéke, valamint a hiba eloszlása.
Numerikus szimulációkkal ellenőrzött hipotézisünk alapján lehetővé válik a felületi pontok elmozdulásának követése, melyhez az időbeli sűrítés szükséges mértékét a pont pályájának záródási hibája alapján az 5. ábrán látható paraméter-tanulmány segítségével meghatároztuk a kézi beavatkozás elkerülése céljából.
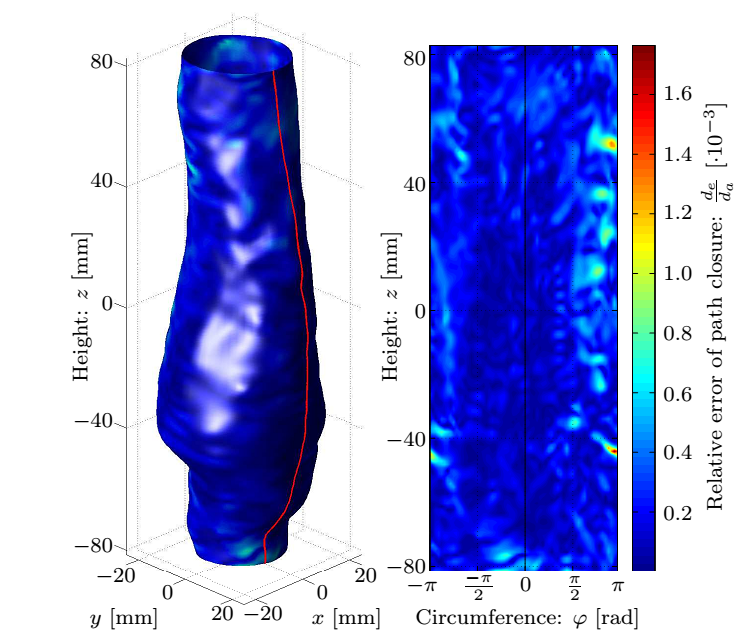
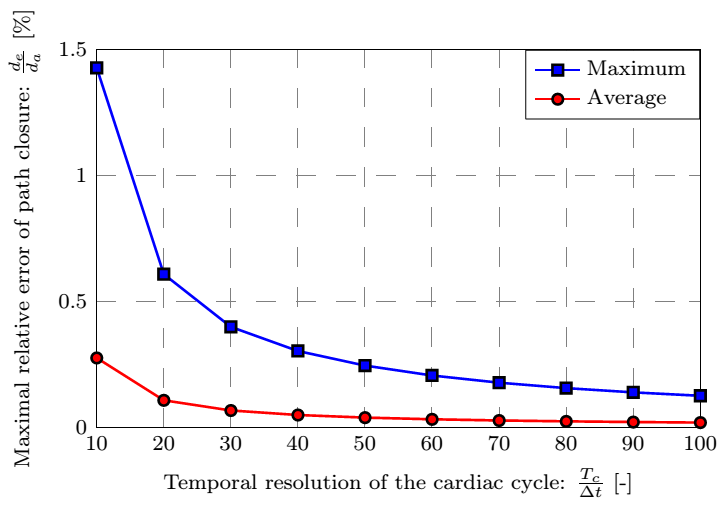
5. ábra: A záródási hiba eloszlása a felületen, valamint annak maximális és átlagos mértéke az időbeli felosztás függvényében.
Az alakváltozások meghatározásához a Kirchhoff-Love-héjelem általánosításával képesek vagyunk figyelembe venni a geometriai és anyagi nemlineáris hatásait.
Eredményül nemcsak az alakváltozások, hanem azok időbeli deriváltjait is meg tudjuk határozni. A 6. ábrán látható, hogy a kerületirányú nyúlások és a referenciasíkra merőleges alakváltozás komponensek dominálnak (10%), és –ahogy azt vártuk – az ábrák közepén lévő tágulatoknál az anyagi merevség növekedésének hipotézisével összhangban ezek egy nagyságrenddel kisebbek, a tágulat határain pedig felveszik maximumaikat. A tengelyirányú megnyúlás a nagy, tengelyirányú görbülettel rendelkező helyeken, míg a síkbeli szögtorzulás az elváltozás szélein domináns.
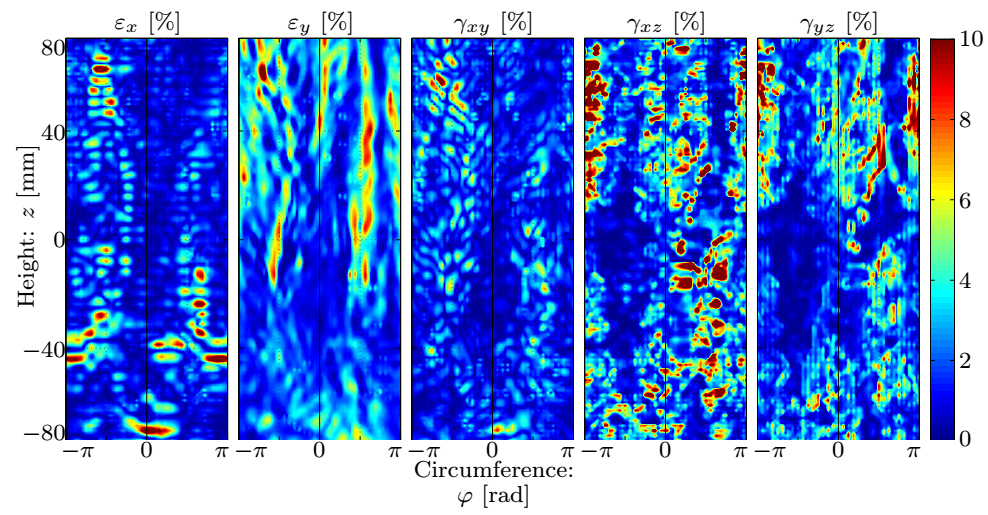
6. ábra: Az alakváltozás-komponensek amplitúdóinak eloszlása.
Anyagi paraméterek indirekt meghatározása
Létrehoztam egy általános módszert, ami rendkívül gyorsan képes végeselemes modellek anyagi paramétereinek beállítására elmozdulási és teher adatok mérése után. Az eljárás fő előnye a célfüggvénygradiens számításának gyorsasága.
Validáció
Az eljárás megfelelőségét és a valóságot jól közelítő voltát már szilikon mintákon elvégeztük, valamint mind a 7. ábrán látható mikroszinten, mind a 8. ábrán bemutatott makroszkopikus, jelenleg is folyó vizsgálatokkal igazolni szeretnénk a kutatás végső fázisában.
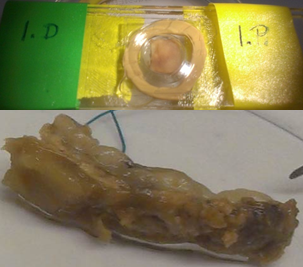
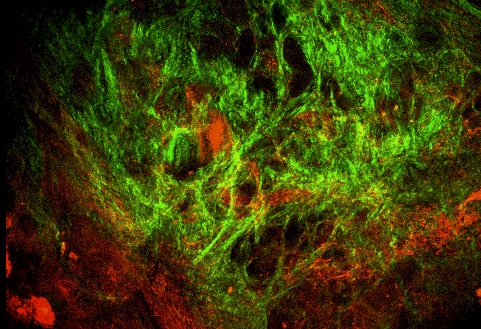
7. ábra: A tágulat falából vett minta és a multifoton mikroszkóp felvétel a kollagén és elasztin rendszerről.


8. ábra: A biaxiális húzókísérlethez használt berendezés és tesztje.
Várható impakt, további kutatás
PhD-kutatásom eredményeképp egy validált, a klinikumban is egyszerűen alkalmazható orvosi döntést segítő szoftver létrehozása várható, amely segítségével a jelenlegi gyakorlatban elterjedtnél megalapozottabb becslés adható az aneurizmák felhasadási kockázatát illetően, ezáltal kiszűrhetővé válnak a kisebb átmérőjű, de ruptúrára hajlamos értágulatok. A részeredmények felhasználását illetően az alakváltozások, de elsősorban a fal anyaga mechanikai paramétereinek és az egyénre szabott roncsolódási fok in-vivo meghatározása a már meglévő módszerek továbbfejlesztéséhez is jelentősen hozzájárul, valamint a kialakulási folyamat mélyebb megértése is lehetővé válik általuk.
Saját publikációk, hivatkozások, linkgyűjtemény
Kapcsolódó saját publikációk listája
S1 Nagy, R., Csobay-Novák, C., Lovas, A., Sótonyi, P., & Bojtár, I., Non-invasive in vivo time-dependent strain measurement method in human abdominal aortic aneurysms: Towards a novel approach to rupture risk estimation. Journal of biomechanics, 48(10), 1876–1886. (2015)
S2 Nagy R., Csobay-Novák Cs., Lovas A., Sótonyi P., Bojtár I.; Towards indirect in-vivo measurement of material properties of aortic aneurysms: Determining the displacement field. In: Oñate E., Oliver J. and Huerta A. (Eds.) 11th World Congress on Computational Mechanics (WCCM XI), Barcelona, 0214.
S3 Robust, C1 continuous surface reconstruction of arbitrary branching pipeline topology, Computers and Structures, (submitted 2016)
S4 Nagy R., Bojtár I.; Improving the clinical decision strategy of aortic aneurysm threatment: in vivo material property identification, 12th International Symposium on Computer Methods in Biomechanics and Biomedical Engineering, Amsterdam, 2014.
S5 Attila Lovas, Róbert Nagy, Elek Csobo, Brigitta Szilagyi, Csaba Csobay-Novák, Péter Sótonyi, Numerical reconstruction of pulsatile blood flow 4D computer tomography data
Computers and Mathematics with Applications, 16 p. (2016)
S6 Nagy Róbert, Bojtár Imre, Numerical Assessment of Geometric and Load Parameters Associated with Intracranial Aneurysm Formation, Oeriodica Polytechnica-Civil Engineering 59:(2) pp. 225–231. (2015)
Hivatkozások listája
H1 Sakalihasan N., Limet R., Defawe O.D.; Abdominal aortic aneurysm, The Lancet, 365, pp.1577–89, 2005. U.K. Small Aneurysm Trial Participants; Final 12-year follow-up of Surgery versus Surveillance in the UK Small Aneurysm Trial, British Journal of Surgery; 94: 702–708, 2007.
H2 D.E. Szilagyi, R.F. Smith, F.J. DeRusso, J.P. Elliott, F.W. Sherrin, Contribution of abdominal aortic aneurysmectomy to prolongation of life,Annals of Surgery, 164(4):678–99, 1966.
H3 D.E. Szilagyi, J.P. Elliott, R.F. Smith, Clinical fate of the patient with asymptomatic abdominal aortic aneurysm and unfit for surgical treatment, Archives of Surgery, 104(4):600–606, 1972.
H4 J.T. Powell, Final 12-year follow-up of Surgery versus Surveillance in the UK Small Aneurysm Trial,British Journal of Surgery, 94(6):702–708, 2007.
H5 D.C. Brewstera, J.L. Cronenwett, J.W. Hallett Jr., K.W. Johnston, W.C. Krupski, J.S. Matsumura}, Guidelines for the treatment of abdominal aortic aneurysms: Report of a subcommittee of the Joint Council of the American Association for Vascular Surgery and Society for Vascular Surgery, Journal of Vascular Surgery, 37(5):1106–1117, 2003.
H6 Raghavan M.L., Kratzberg J., Castro de Tolosa E.M., Hanaoka M.M., Walker P., da Silva E.S.; "Regional distribution of wall thickness and failure properties of human abdominal aortic aneurysm". Journal of Biomechanics 39 (16): 3010–6. 2006. doi:10.1016/j.jbiomech.2005.10.021. PMID 16337949.
H7 Fillinger M.F., Raghavan M.L., Marra S.P., Cronenwett J.L., Kennedy F.E.; "In vivo analysis of mechanical wall stress and abdominal aortic aneurysm rupture risk". Journal of Vascular Surgery 36 (3): 589–97. 2002. doi:10.1067/mva.2002.125478. PMID 12218986.
H8 Holzapfel G.A., Gasser T.A., Ogden R.W.; A new constitutive framework for arterial wall mechanics and a comparative study of material models, J. Elasticity, Vol. 61, pp. 1–48, 2000.
H9 Hughes, T. J., Cottrell, J. A., & Bazilevs, Y. (2005). Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement.Computer methods in applied mechanics and engineering, 194(39), 4135–4195.
H10 Bárdossy G., Halász G.; Modeling blood flow in the arterial system. Periodica Polytechnica 55, 49–55. 2011
