|
|
BMe Research Grant |
|
Pál Vásárhelyi Doctoral School of Civil Engineering and Earth Sciences
BME Department of Structural Mechanics
Supervisor: Dr. Bojtár Imre
Mechanics of the Development and Rupture of Aneurysms
Introducing the research area
The topic of my research is the biomechanical analysis of peccant, localized and irreversible dilations (aneurysms) of the human arterial system. The main occurrences are at the bifurcation tips of the cerebral arterial system and the abdominal part of the main aorta descending from the heart. On the one hand, ensuing rupture of these lesions is extremely hazardous, with lethal outcomes in the overwhelming majority of the cases, while the elective repair by open surgery or endovascular stent grafting still remains a high risk procedure on the other. Since the advent of modern imaging technologies and regular screening tests, these otherwise asymptomatic aortic deformations are often discovered at an early stage. Yet, the reasons of both the development and the abrupt rupture is unknown, hence, regarding the management process, the clinical practice has only statistical data to rely on. My algorithm is capable of patient-specific, quick and non invasive rupture risk assessment enabling the selection of management procedure and aiding the installation of operation hierarchy as well on strong biomechanical considerations.
Brief introduction of the research place
I pursue my research at the Department of Structural Mechanics, where beyond basic mechanical research, structural optimization and innovative engineering developments together with various up-to-date problems arising in the interdisciplinary field of biomechanics are also dealt with, in close cooperation with practicing medical doctors. My supervisor, Prof. Imre Bojtár is a pioneer in the Hungarian biomechanical society and discipline and was the founding director of the Biomechanical Cooperative Research Center.
History and context of the research
The rupture of an aneurysms is caused by complex, local biomechanical stimuli. From a pure mechanical point of view, failure occurs, when the blood flow induced stress state of the wall reaches beyond the ultimate strength of the tissue. The simplest consequence of this principle is the qualitative verification by the Young-Laplace equation of the well observed rule of the thumb: the risk of rupture increases with the dilated diameter [H1]. 5.5 cm is the statistical limit [H2, H3], where the possibility of rupture exceeds the risk of the operation [H4].
In real cases, smaller aneurysms can also fail [H5], thus, due to the complex geometry, material model, boundary conditions, dynamic behavior and the inhomogeneous material parameters such lucid and general conclusions are impossible to make. Therefore, researchers of the discipline turned towards the numerical tools of engineering. Commercial softwares provide the possibility of patient-specific stress determination by handling the liquid blood and the solid wall phases separately and solving the respective differential equations via finite volume (FV) and finite element (FE) simulations in a fully coupled fluid-structure interaction (FSI) algorithm [H6, H7].
The procedure requires competent expertise and demanding resources hindering its launch to everyday use. Furthermore, being irrespective of the observed decrease in the failure criterion and stress concentration resulting from the significant rigidity increase and the local stiffening in the bulge region, its usage is strongly criticized. The main obstacle behind these flaws is the lack of knowledge on the actual spatial distribution of the material parameters in the living tissue (in vivo), although an adequate hyper-elastic material model [H8] determined on a micro-structural basis is at our disposal to feed them in.
Aims of the research
Within my PhD research, I am working on the development and computational implementation of a simple and quick decision algorithm amending the above stated flaws being readily applicable in clinical practice. The backbone of this method is a quick optimization algorithm based on the inverse application of the novel paradigm of FE algorithms (IGA, [H9]), through which the patient-specific inhomogeneous parameters of the material model connecting the measured strain and load fields are determined in-vivo, which is indispensable for the calculation of the real stress distribution.
Applying the method to the healthy parts of the aorta in the same patient, the tailor-made measurement and calibration of the degree of degradation becomes possible allowing the deduction of the changes in the failure criterion based on measurements of in vitro dissections. Furthermore, we establish a new rupture criterion based on the degree of degradation.
We validate the methodology by samples dissected during the operation of patients undergoing open surgery by determining the macroscopic mechanical properties via biaxial tensile tests and the micro-structure arising from the orientation of the main wall constituents via multiphoton microscopy and histological methods. The interdisciplinarity of the topic demands the close collaboration of the disciplines while the application oriented goal requires the constant feedback from the practice, therefore the Heart and Vascular Research Center, the Institute of Human Physiology and Clinical Experimental Research
and the Department of Biophysics and Radiation Biology at Semmelweis University; the Vascular Biomechanics and Biofluids Laboratory at University of Texas San Antonio, and the Department of Hydrodynamic Systems and the Department of Geometry at BME also play an essential role in the project.
Methods
The research project comprises five distinct parts as seen in Fig. 1:
- development of the algorithms for the determination of strain field,
- the automatic load field generation,
- the material parameter identification through optimization,
- the experimental validation, and
- the determination of the degree of material degradation.
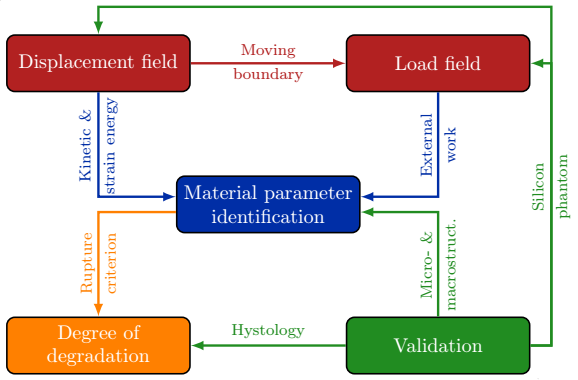
Figure 1: Flowchart of the research process
Strain field
An ECG-Gated CTA capable Philips Brilliance iCT 256 device available at the Cardiovascular Research Center is used to scan the abdomen with slice thickness of 1 mm and transverse voxel size of 0.4883 mm. The reconstruction is performed at 10 discrete time steps of the stabilized R-R intervals with an active contour algorithm. This way we are able to follow in time the flow domain shape (lumen) given by its points, which serves as our input data [S1].
The measurement error is approximated by the transverse voxel size and is not negligible compared to the displacement amplitude. I compensate for this shortcoming by the smoothing of the surface in both space and time yielding an analytic description [S3].
Having subtracted the rigid body motions, I determined the displacements of surface points. The underlying principle is based on FSI simulation observations, notably after sufficiently increasing the temporal resolution of the surface definition exploiting the functional relation, the displacement direction of the points is assumed to align with the local normal of the reference surface, and finally ensuring the periodicity, the closure error of the path is linearly distributed along it.
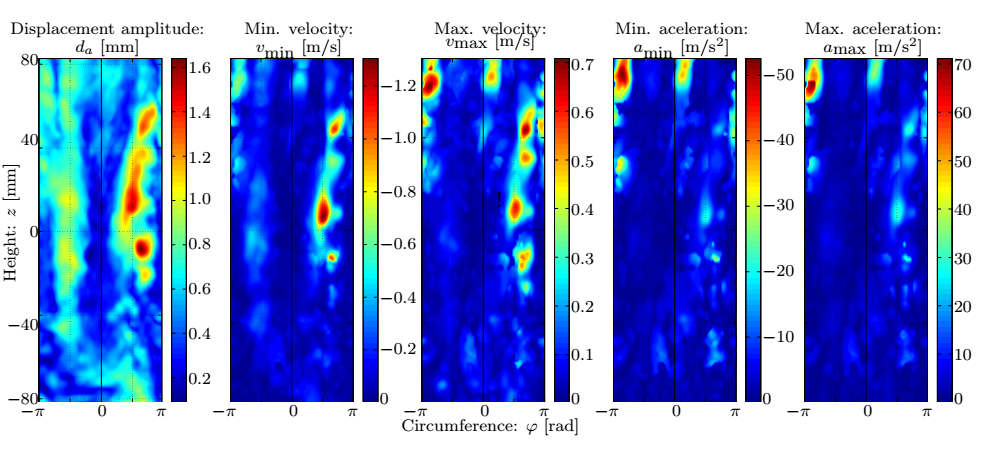
Figure 2: The kinematic variables of the reference surface [S2].
For determining the strain and strain-rate field I utilized the toolbox of the shell theory and the finite element method by an extended version of the Kirchhoff-Love theory, rejecting the assumption of undeformable fibres perpendicular to the reference surface.
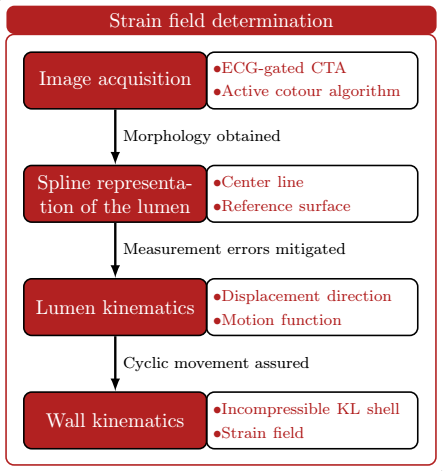
Figure 3: Steps of strain field determination.
Load field
The input data for the fluid simulation is the measured pressure profile, which is transformed to the desired arterial section by a 1D model [H10]. A tube is attached to the inlet cross-section to develop the time dependent velocity profile. Analogously, the following arterial sections are taken into account by a negative impulse and mass source attached to the outlet cross-section. By the knowledge of the wall motion I evade the time consuming FSI simulation and the loads acting on the wall yield from a simple transient CFD calculation.
Material parameters
In the discretized version of the equations of motions only the stiffness matrix depends on the unknown constant material parameters. The damping matrix is neglected at the moment, but in the future I will apply a Rayleigh damping, the parameters of which are to be determined from the energy dissipation of samples excited at the well defined frequency of the heartbeat. The Levenberg-Marquardt optimization algorithm minimizes the norm of the difference of the load vector calculated from the displacement field and that from the fluid simulations with proper constraints postulated on the material parameters. The process is remarkably fast partly because there is no need for inverting the stiffness matrix, and partly because exploiting the peculiarities of the FE method, the calculation time of the step direction in the parameter field is reduced to the order of magnitude of a simple function evaluation, consequently the abundance of unknowns (~105) causes no difficulties.
Validation
At the final stage of the research biaxial tensile tests are carried out on the specimens in less than an hour after the operation, then histological and multiphoton microscopic analyses are performed to validate the model.
Results
From the above presented five cornerstones of the method I have completed the displacement field calculation [S1] and the optimization algorithm. The validation using silicon phantoms and the preparation of the experimental methodology are also done, the necessary equipment and circumstances are now available. The publication of the midterm results is in process alongside with the automatization of the fluid model.
In-vivo strain measurement
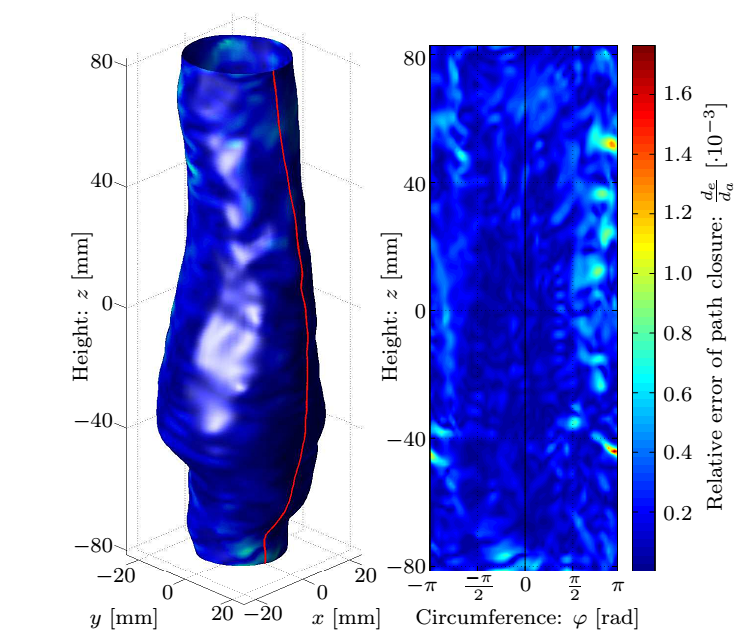
Currently we are able to determine the in vivo strains automatically, for which the following smoothing parameters were concluded during the parameter studies presented in Fig. 4: the patch size of the 2D bicubic B-spline and the amplitude criterion of the noise filter applied in the frequency domain after Fourier transformation, finally providing an analytic description of the lumen.
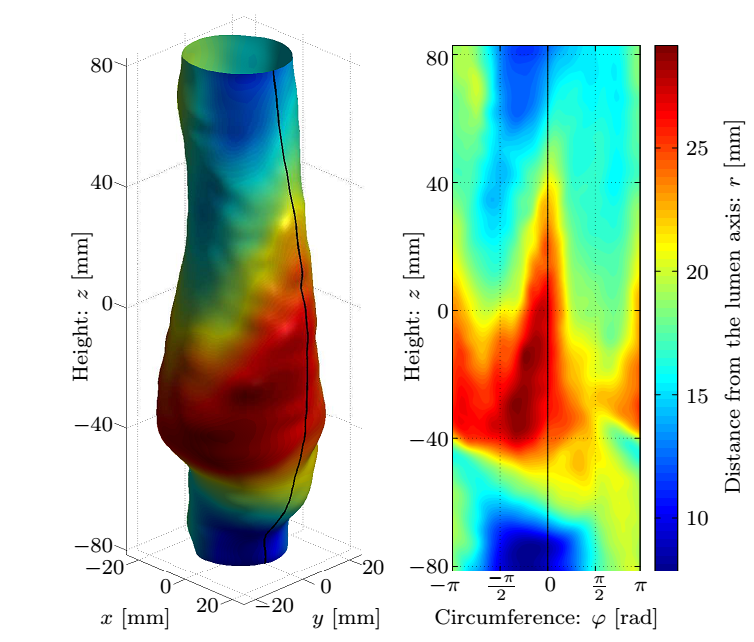
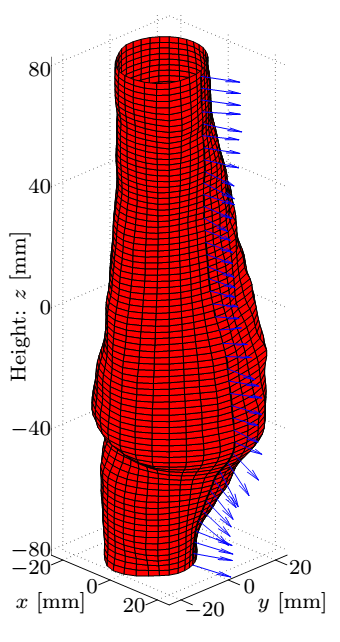

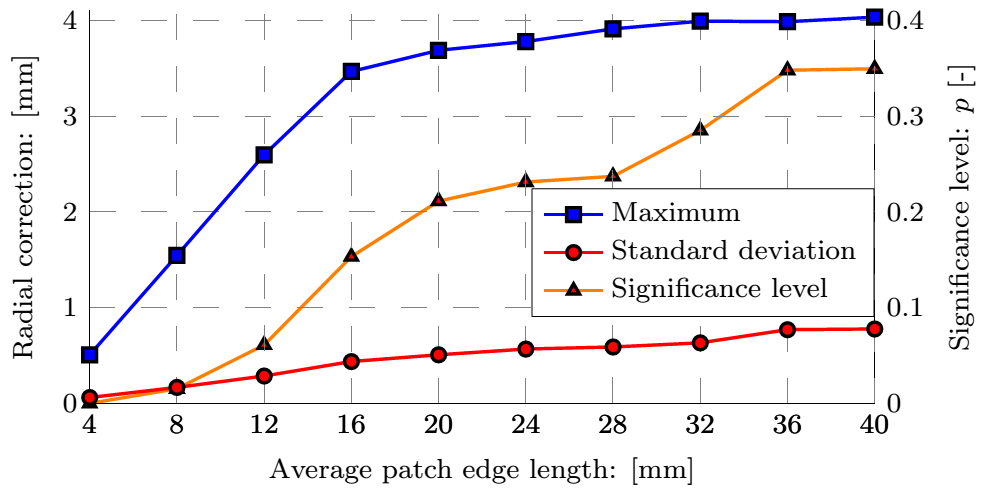
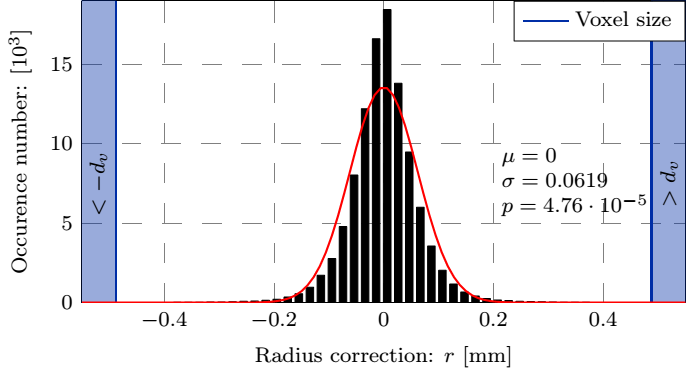
Figure 4: Top row: Geometry of the dilatation, the smoothed surface and the corresponding normals, and the distance of measured coordinates from the fitted surface. Bottom row: The maximal and average values of the correction as a function of the patch size and the distribution of the error.
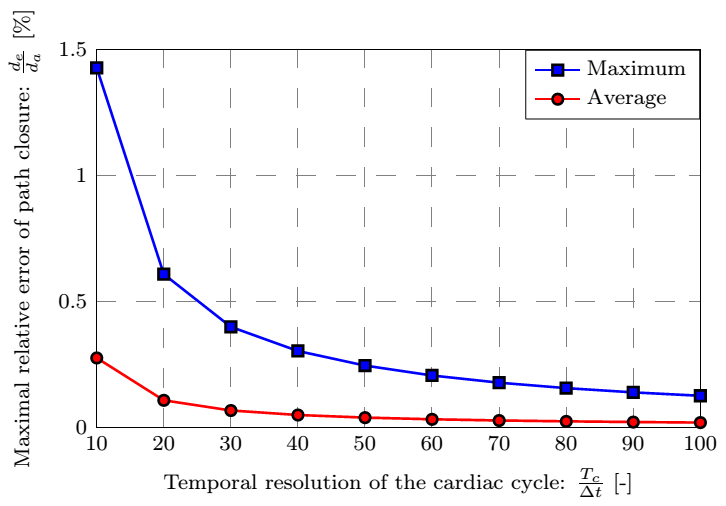
Based on our numerically tested hypothesis the surface points become possible to be followed, for which the necessary rate of temporal resolution is determined by a parameter study shown in Fig. 5 to avoid manual intervention.
|
|
|
Figure 5: Distribution of the closure error and its maximal and average values as a function of the temporal resolution.
Generalizing the Kirchhoff-Love shell element, we can account for the material and geometric nonlinear effects.
The results include not only the strains but their time derivatives as well. Fig. 6 shows that the circumferential and the transverse shear components dominate (10%), and in accordance with our expectations regarding the stiffening of the material at the dilated part, the strains in the center of the picture are an order of magnitude smaller reaching their maximum at the edges of the bulge region along with the in-plane shear component. The axial strain increases at locations with high axial curvatures.
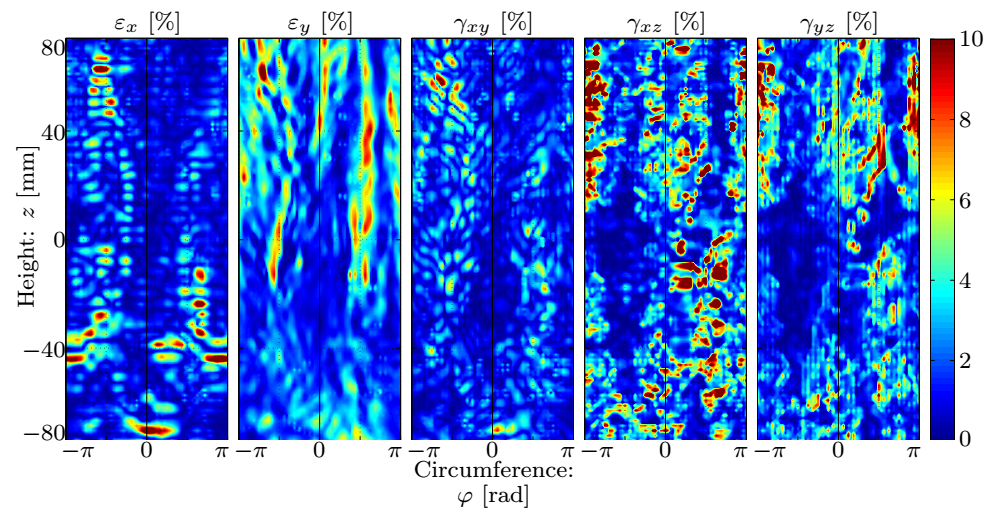
Figure 6: Distribution of the strain component amplitudes.
Indirect material parameter identification
I established a general methodology capable of identifying the material parameters of FE models having the measured displacement and load data at our disposal. The main advantage of the process is the fast computation of the gradient of the goal function.
Validation
At the final stage of the research we are going to validate the adequacy of the model both on micro- (Fig. 7) and macroscale (Fig. 8).
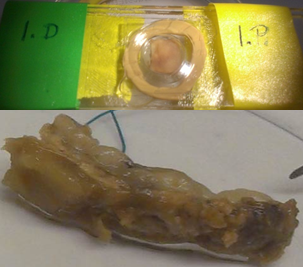

Figure 7: The sample taken from the aneurysm wall and the multiphoton microscopy image showing the collagen and elastin system.


Figure 8: The assembly for the biaxial tensile experiment and the test of the device.
Expected impact and further research
As a result of my PhD research, we expect a simple, quick and validated algorithm assisting the decision on aneurysm management in clinical practice providing novel, more relevant and well-established assessment on the rupture risk. In this way we can filter out to operate the small but rupture-prone dilatations. Regarding the usage of the midterm results, the in vivo determination of displacements but especially the material properties of the wall and patient specific calibrated degree of degradation improve significantly the state of the art and contribute to the deeper understanding of the pathogenic process.
Publications, references, links
Related own publications
S1 Nagy, R., Csobay-Novák, C., Lovas, A., Sótonyi, P., & Bojtár, I., Non-invasive in vivo time-dependent strain measurement method in human abdominal aortic aneurysms: Towards a novel approach to rupture risk estimation. Journal of biomechanics, 48(10), 1876–1886. (2015)
S2 Nagy R., Csobay-Novák Cs., Lovas A., Sótonyi P., Bojtár I.; Towards indirect in-vivo measurement of material properties of aortic aneurysms: Determining the displacement field. In: Oñate E., Oliver J. and Huerta A. (Eds.) 11th World Congress on Computational Mechanics (WCCM XI), Barcelona, 0214.
S3 Robust, C1 continuous surface reconstruction of arbitrary branching pipeline topology, Computers and Structures, (submitted 2016)
S4 Nagy R., Bojtár I.; Improving the clinical decision strategy of aortic aneurysm treatment: in vivo material property identification, 12th International Symposium on Computer Methods in Biomechanics and Biomedical Engineering, Amsterdam, 2014.
S5 Attila Lovas, Róbert Nagy, Elek Csobo, Brigitta Szilagyi, Csaba Csobay-Novák, Péter Sótonyi, Numerical reconstruction of pulsatile blood flow 4D computer tomography data
Computers and Mathematics with Applications, 16 p. (2016)
S6 Nagy Róbert, Bojtár Imre, Numerical Assessment of Geometric and Load Parameters Associated with Intracranial Aneurysm Formation, Periodica Polytechnica-Civil Engineering 59:(2) pp. 225–231. (2015)
Reference list
H1 Sakalihasan N., Limet R., Defawe O.D.; Abdominal aortic aneurysm, The Lancet, 365, pp.1577–89, 2005. U.K. Small Aneurysm Trial Participants; Final 12-year follow-up of Surgery versus Surveillance in the UK Small Aneurysm Trial, British Journal of Surgery; 94: 702–708, 2007.
H2 D.E. Szilagyi, R.F. Smith, F.J. DeRusso, J.P. Elliott, F.W. Sherrin, Contribution of abdominal aortic aneurysmectomy to prolongation of life,Annals of Surgery, 164(4):678–99, 1966.
H3 D.E. Szilagyi, J.P. Elliott, R.F. Smith, Clinical fate of the patient with asymptomatic abdominal aortic aneurysm and unfit for surgical treatment, Archives of Surgery, 104(4):600–606, 1972.
H4 J.T. Powell, Final 12-year follow-up of Surgery versus Surveillance in the UK Small Aneurysm Trial,British Journal of Surgery, 94(6):702–708, 2007.
H5 D.C. Brewstera, J.L. Cronenwett, J.W. Hallett Jr., K.W. Johnston, W.C. Krupski, J.S. Matsumura}, Guidelines for the treatment of abdominal aortic aneurysms: Report of a subcommittee of the Joint Council of the American Association for Vascular Surgery and Society for Vascular Surgery, Journal of Vascular Surgery, 37(5):1106–1117, 2003.
H6 Raghavan M.L., Kratzberg J., Castro de Tolosa E.M., Hanaoka M.M., Walker P., da Silva E.S.; "Regional distribution of wall thickness and failure properties of human abdominal aortic aneurysm". Journal of Biomechanics 39 (16): 3010–6. 2006. doi:10.1016/j.jbiomech.2005.10.021. PMID 16337949.
H7 Fillinger M.F., Raghavan M.L., Marra S.P., Cronenwett J.L., Kennedy F.E.; "In vivo analysis of mechanical wall stress and abdominal aortic aneurysm rupture risk". Journal of Vascular Surgery 36 (3): 589–97. 2002. doi:10.1067/mva.2002.125478. PMID 12218986.
H8 Holzapfel G.A., Gasser T.A., Ogden R.W.; A new constitutive framework for arterial wall mechanics and a comparative study of material models, J. Elasticity, Vol. 61, pp. 1–48, 2000.
H9 Hughes, T. J., Cottrell, J. A., & Bazilevs, Y. (2005). Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Computer methods in applied mechanics and engineering, 194(39), 4135–4195.
H10 Bárdossy G., Halász G.; Modeling blood flow in the arterial system. Periodica Polytechnica 55, 49–55. 2011