|
|
BMe Kutatói pályázat |
|
BME Informatikai Tudományok Doktori iskola
BME VIK, Távközlési és Médiainformatikai tanszék
Témavezető: Dr. Pap Zoltán
Inkrementális tesztgeneráló algoritmusok
A kutatási téma néhány soros bemutatása
Egy új szoftver vagy hardver termék fejlesztésénél a körültekintő tesztelés elengedhetetlen.
Kutatásom során olyan új algoritmusok kifejlesztésével foglalkozom, amelyek képesek egy formális modellel megadott rendszer tesztkészletének karbantartására az abban végbemenő változtatások során. A javasolt eljárások a változtatás előtti rendszer adatainak felhasználásával lényegesen hatékonyabban képesek az új, változtatott rendszerre tesztkészletet készíteni, mint az eddigi eljárások.
A kutatóhely rövid bemutatása
Kutatásomat a Budapesti Műszaki és Gazdaságtudományi Egyetem Távközlési és Médiainformatikai Tanszékének a Nagysebességű hálózatok laboratóriumának (HSNLab) támogatásával végzem. A tanszék és a kutatólaboratórium az egyetem Hálózati Rendszerek és Szolgáltatások Tanszékével, az ELTE Kommunikációs Hálózatok Laboratóriumával (CNL), valamint az ipari partner Ericsson-nal szoros kapcsolatokat ápol.
A kutatás történetének, tágabb kontextusának bemutatása
Mind a hardver-, mind a szoftverfejlesztés során a termékek ellenőrzése, megfelelőségének vizsgálata a minőségbiztosítás egy fontos állomása. A nagy, komplex rendszerek folyamatosan fejlődnek, hogy megfeleljenek az időközben felmerülő új követelményeknek. Minden egyes fejlesztési lépésben – ahol a rendszer specifikációjának változtatása mellett előállítunk egy új, annak megfelelő implementációt is – a tesztelésnek is változnia kell. A tesztelés kézi módosítgatása esetleges, ezért automatikus tesztgeneráló eljárások alkalmazása szükséges.
Habár az automatikus tesztgenerálás témaköre a szakirodalom által jól feldolgozott terület [1][2][3], a publikált eljárások zöme mégsem kezeli hatékonyan a specifikációban végbemenő változtatásokat.
A legtöbb tesztgeneráló algoritmus ún. batch algoritmus, amelynek kimenete – a rendszerre adott f(y) tesztkészlet – csupán az aktuális bemenettől – az y rendszerleírástól – függ (1. ábra). Egy ilyen algoritmus teljesen az alapokról építi újra a tesztkészletet (f(y’)), még abban az esetben is, ha a rendszer specifikációjában csak minimális változtatások történtek. Nem nehéz belátni, hogy ez a megközelítés kisebb változtatások esetén rendkívül erőforráspazarló.
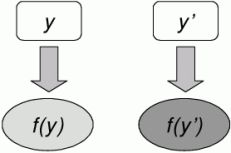
1. ábra: Batch algoritmus
A probléma hatékony kezelése új, úgynevezett inkrementális algoritmusokkal oldható meg. Az inkrementális tesztgeneráló algoritmusok (2. ábra) bemenete egyaránt tartalmazza a a változtatás előtti rendszerleírást (y), az azon végrehajtott változtatást (dy), valamint a rendszer előző verziójához tartozó tesztkészletet (f(y)). Kimenete – a batch algoritmussal megegyező módon – az új rendszerre (y’) adott tesztkészlet (f(y’)). Azáltal, hogy az inkrementális algoritmus felhasználja a rendszer egy előző változatához készített kimenetét, képes lehet az új, megváltozott rendszerre sokkal hatékonyabb megoldást adni.
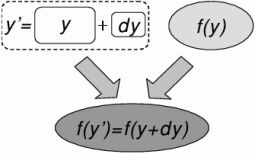
2. ábra: Inkrementális algoritmus
A kutatás célja, a megválaszolandó kérdések
A kutatás célja olyan inkrementális tesztgeneráló algoritmusok kifejlesztése volt, amelyek futási ideje nem a rendszer méretétől, hanem a rendszerben végbemenő változtatások hatásának méretétől függ, miközben olyan kimenetet adnak, amelyek formája és hibafelderítő képessége megegyezik a batch algoritmusok által nyújtottakéval. Az inkrementális tesztgeneráló eljárások által hatékony megoldást lehetne adni folyamatosan változó rendszerek tesztelésére és teszt generálására.
Az algoritmus formális leírásán és implementálásán kívül analitikus komplexitás-elemzések is szükségesek voltak annak vizsgálatára, hogy az algoritmusok futási ideje hogyan függ a változtatások hatásának méretétől és hogyan viszonyul a batch algoritmusok futási idejéhez.
További cél volt olyan széles körű szimulációk végzése, amelyek megmutatják, hogy az algoritmus futási ideje milyen mértékben függ az egyes bemeneti paraméterektől, vagyis az egyes változtatások típusa, száma, valamint a specifikáció egyes paraméterei (állapotok száma, lehetséges bemenetek és kimenetek száma) milyen hatással vannak a változtatásban érintett terület méretére, valamint az algoritmus futási idejére mind önmagában véve, mind pedig a többi batch algoritmussal összevetve.
Fontos megemlíteni, hogy a kutatás kezdetekor csupán egyetlen (véges automatán alapuló) inkrementális tesztgenerálással foglalkozó írás létezett [4], ez azonban csak néhány ritkán előforduló triviális esetet kezelt, ráadásul mivel futási ideje nem a változtatás hatásának méretétől, hanem a rendszerspecifikáció méretétől függött, nem is tekinthető igazi inkrementális eljárásnak [C1].
Módszerek
Az egyik széles körben alkalmazott automatikus tesztelési módszer az úgynevezett véges automata alapú fekete doboz konformancia-tesztelés (3. ábra). Ebben az esetben mind az implementációt, mind a specifikációt egy véges automatával, vagy más néven állapotgéppel modellezzük; az implementáció automatáját egy ismeretlen belső működésű fekete doboznak feleltetjük meg, míg a specifikáció automatáját egy ismert belső működésű fehér doboz reprezentálja. A tesztelés során mindkét automatának adunk bemeneti tesztszekvenciákat, majd az erre adott kimeneti válaszok összevetésével megvizsgáljuk, hogy az implementáció állapotgépe megfelel-e a specifikáció állapotgépének (3. ábra).
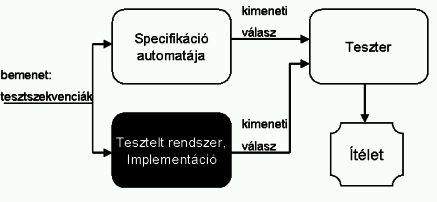
3. ábra: Véges automata alapú konformancia-tesztelés
Több eljárás született a véges automata alapú fekete doboz konformancia-tesztelés megvalósítására, amelyek különböző méretű és felépítésű tesztkészlettel és hibafelderítő képességgel rendelkeznek.
Az egyik ilyen eljárás a TT-metódus (Transition Tour method, vagy Állapotátmeneti Séta módszer) [5], amely erősen összefüggő, determinisztikus véges automaták számára készít tesztkészletet. Ez a tesztkészlet egyetlen tesztszekvenciából áll, amely a bemenetként megadott specifikáció összes állapotát és állapotátmenetét végigjárja és minimális hosszúságú [6]. A TT-metódus egy, már korábban megoldott matematikai probléma, az úgynevezett Irányított Kínai Postás Probléma [7] algoritmusát használja a tesztszekvencia elkészítéséhez.
Egy másik ismert véges automata alapú konformanciateszt-készítő eljáráscsoport a W/Wp/HIS-metódus hármas [8][9][10][11]. Ezek bizonyos, a specifikáció automatájára vonatkozó feltételek teljesülése esetén (a specifikáció véges automatája legyen erősen összefüggő, determinisztikus, minimál és megbízható reset üzenettel rendelkezzen) garantálják az automatában felléphető összes kimeneti és következő állapot hiba megtalálását. A tesztkészlet – ellentétben az előbb ismertetett TT-metódussal – strukturált felépítésű: egy állapotok elérésére és egy állapotok ellenőrzésére szolgáló részt tartalmaz. A három eljárásból a Wp [9] és HIS [10][11] metódus a leghatékonyabb, e között a kettő között csupán a végső tesztet érintő formai eltérések vannak (a HIS-metódus kimenete szigorúbb szabályozású, ezért áttekinthetőbb).
Eddigi eredmények
Kutatásom során kifejlesztettem két különböző inkrementális tesztgeneráló eljárást, amelyek az előző fejezetben ismertetett batch algoritmusok, a TT és HIS metódus szerkezetén alapulnak; ezek tesztkészletét tartják karban a rendszert érintő változások függvényében. A két különböző eljárás más és más megkötéseket alkalmaz a specifikáció állapotgépére vonatkozóan, más hibalefedettséget biztosít eltérő tesztkészlet felépítés és hossz mellett, így skálázhatósági lehetőséget teremt a tesztmérnök számára.
A HIS-metódus tesztkészletét karbantartó eljárásom biztosítja minden következő állapot és kimenet hiba megtalálását abban az esetben, ha a specifikáció véges automatája kielégít bizonyos feltételeket (az automata teljesen specifikált, determinisztikus, megbízható reset üzenettel rendelkezik és minimál). Az eljárás két részből áll, amelyek együtt elkészítik a rendszer teljes tesztelésére szolgáló tesztkészletet, de akár külön-külön is használhatóak különféle tesztelési részfeladatok (állapotelérés és állapotellenőrzés) vagy a rendszert leíró állapotgép bizonyos feltételeinek (automata erősen összefüggő vagy minimál-e) ellenőrzésére.
A TT-metódus tesztkészletét karbantartó eljárásom kevesebb megkötést alkalmaz a specifikáció állapotgépére vonatkozóan, több fajta változtatást enged meg a rendszert leíró modellen és a HIS-metódusénál jóval kisebb tesztkészletet generál. Jóllehet az állapotgép összes állapotát és állapotátmenetét lefedi, csak a kimeneti hibák megtalálását garantálja, tehát a HIS-metódus tesztkészletére írt eljárásnál kisebb hibafelderítő képességgel rendelkezik.
Az elkészült eljárásokat konferencia- és folyóiratcikkekben formálisan is leírtam [C1][J2], továbbá meg is valósítottam őket. Az inkrementális algoritmusok hatékonyságát mind analitikusan [C1][J2], mind kiterjedt szimulációk segítségével igazoltam [C6][J2]. Az analitikus komplexitás számolások rámutattak, hogy az algoritmusok hatékonysága kizárólag a változtatás hatásának méretétől függ, a rendszerspecifikáció méretétől nem. Legrosszabb esetben – amikor a változtatás hatása az egész rendszerre kiterjed – eljárásom komplexitása megegyezik a batch algoritmusokéval. Tipikus esetekben azonban a változtatás csak a rendszer kis részét érinti, ekkor algoritmusaim hatékonysága akár több nagyságrenddel is jobb lehet, mint a felváltani szándékozott, hagyományos batch algoritmusoké. Hogy ez a nyereség gyakorlatban milyen nagy lehet, azt részletes, több paraméter érték alapos vizsgálatára kiterjedő szimulációkkal vizsgáltam meg. Az eredmények rámutattak arra, hogy még kiterjedt változtatások esetén is több nagyságrenddel gyorsabbak a kifejlesztett inkrementális algoritmusok, mint a hagyományos, batch algoritmusok, továbbá a rendszerek méretével az inkrementális algoritmusok hatékonysága tovább nő a hagyományos batch eljárásokhoz képest.
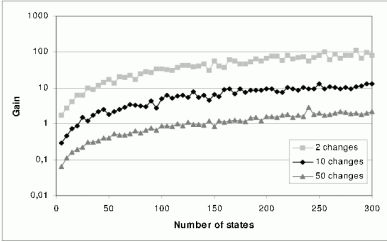
4. ábra: Az inkrementális HIS első felének nyeresége a hagyományos batch HIS-metódussal szemben
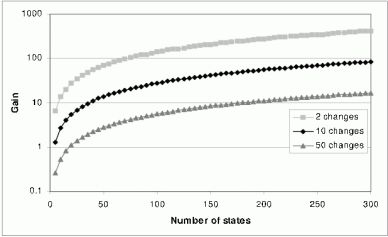
5. ábra: Az inkrementális HIS második felének nyeresége a hagyományos batch HIS-metódussal szemben
A 4. ábra az inkrementális HIS első felének, míg az 5. ábra az inkrementális HIS második felének hatékonyságát mutatja a hagyományos HIS-metódussal szemben 2, 10 és 50 állapotátmenet végállapot megváltoztatása esetén az automata állapotszámának függvényében (állapotátmenetek száma 5 db/állapot, tehát például 10 állapot esetén összesen 50).
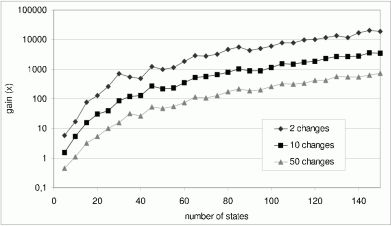
6. ábra: Az inkrementális TT algoritmus nyeresége a hagyományos batch TT-metódussal szemben
A 6. ábra az inkrementális TT algoritmus hatékonyságát mutatja a hagyományos TT-metódussal szemben 2, 10 és 50 állapotátmenet változása esetén az automata állapotszámának függvényében (kimenő állapotátmenetek száma átlagosan 5 db/állapot, tehát például 10 állapot esetén összesen 50).
Várható impakt, további kutatás
Az inkrementális HIS algoritmust bemutató első cikkre [C1] több független hivatkozás született a témában elismert, nemzetközi szaktekintélyektől releváns konferencia- és folyóirat-kiadványban, valamint egy PhD munkában [R1]-[R5].
A második inkrementális eljárást, az inkrementális TT algoritmust ismertető folyóiratcikkünk [J2] ebben az évben jelent meg, a későbbiekben erre is várhatóak szakmai hivatkozások.
A doktori iskola kezdetekor eredetileg kitűzött célokat sikerült teljesíteni. További lehetséges kutatási terület az eljárás kiterjesztése más modellekre, például Kiterjesztett Véges Automatára vagy egyéb, nem véges automata rendszerekre. Szintén érdekes feladat az eljárás integrálása valós tesztrendszerekbe és az ott tapasztalt gyakorlati észrevételek visszacsatolása az algoritmusok még hatékonyabbá tételére, vagy kiegészítése más, esetleg szükséges tulajdonságokkal. Egy ilyen gyakorlati alkalmazási terület lehet automatikus szoftvertesztelés megvalósítása folyamatosan változó rendszerekben.
Saját publikációk, hivatkozások, linkgyűjtemény
Kapcsolódó saját publikációk listája.
[J1] G. Kovács, G. Á. Németh, Z. Pap, and M. Subramaniam: Deriving compact test
suites for telecommunication software using distance metrics. In Journal of Communications Software and Systems, Volume: 5 Number: 2
[J2] G. Á. Németh and Z. Pap: Incremental Maintenance of Transition Tour. In Fundamenta Informaticae, Volume: 129 Number: 3
[B1] G. Á. Németh: Protocol Operation. In Advanced Communication Protocol Technologies: Solutions, Methods and Applications. Hershey; New York: IGI Global, Information Science Reference, 2011. pp. 20–37.
[B2] G. Kovács, G. Á. Németh and Z. Pap: Convergence of fix and mobile networks. In Advanced Communication Protocol Technologies: Solutions, Methods and Applications. Hershey; New York: IGI Global, Information Science Reference, 2011. pp. 226–246. Lecture
[C1] Z. Pap, M. Subramaniam, G. Kovács and G. Á. Németh: A Bounded Incremental Test Generation Algorithm for Finite State Machines. In Proc., Testcom/Fates 2007, Tallinn, Estonia, June 2007.
[C2] G. Kovács, G. Á. Németh, Mahadevan Subramaniam and Zoltán Pap: Optimal String Edit Distance Based Test Suite Reduction for SDL Specifications. In Proc., SDL 2009, Bochum, Germany, September 2009.
[C3] G. Adamis, A. Wu-Hen-Chang, G. Á. Németh, L. Erős, G. Kovács: Data Flow Testing in TTCN-3 with a Relational Database Schema. In Proc., SDL 2013, Montreal, Canada, June 2013.
[C4] G. Kovács, G. Á. Németh, Z. Pap, and M. Subramaniam: Deriving compact test suites for telecommunication software using distance metrics. In Proc., SoftCOM 2008, Split-Dubrovnik, Croatia, September 2008.
[C5] G. Németh and G. Á. Németh: A Generic Model for Advanced Networks Handling Imprecise Information. In Proc., SoftCOM 2009, Hvar, Croatia, September 2009.
[C6] G. Á. Németh, Z. Pap and G. Kovács: The Incremental Maintenance of a Checking Sequence. In Proc., AACS’13, Budapest, Hungary, June 2013.
[C7] G. Á. Németh and Z. Pap: Inkrementális tesztgenerálás. In Tavaszi Szél 2012,
Győr, Hungary, 2012.
Hivatkozások listája.
[1] M. Broy, B. Jonsson, J.-P. Katoen, M. Leucker and A. Pretschner (Eds.), Model-Based Testing of Reactive Systems (Springer-Verlag, New York, 2005).
[2] R. Dorofeeva, K. El-Fakih, S. Maag, A. R. Cavalli, N. Yevtushenko, Fsm-based conformance testing methods: A survey annotated with experimental evaluation, Information and Software Technology 52(12) (2010): 1286–1297.
[3] D. Lee and M. Yannakakis. Principles and Methods of Testing Finite State Machines – A Survey. Proceedings of the IEEE, 84(8):1090–1123, 1996.
[4] Rita Dorofeeva, Khaled El-Fakih, Stephane Maag, Ana R. Cavalli, and Nina Yevtushenko. FSM-based conformance testing methods: A survey annotated with experimental evaluation. Information and Software Technology, 52(12):1286– 1297.
[5] S. Naito, M. Tsunoyama. Fault detection for sequential machines by transition-tours. in Proceedings of the 11th IEEE Fault-Tolerant Computing Conference (1981): 238–243.
[6] Mark Utting, Bruno Legeard. Practical Model-Based Testing: A Tools Approach. Morgan Kaufmann Publishers Inc., San Francisco, CA, USA, 2007.
[7] Jack Edmonds and Ellis L. Johnson. Matching, Euler tours and the Chinese postman. Mathematical Programming (1973) 5(1): 88–124.
[8] T. Chow. Testing software design modeled by finite-state machines. IEEE Transactions on Software Engineering, 4(3):178–187, May 1978.
[9] S. Fujiwara, G. v. Bochmann, F. Khendec, M. Amalou, and A. Ghedamsi. Test selection based on finite state model. IEEE Transactions on Software Engineering, 17(6):591–603, 1991.
[10] A. Petrenko, N. Yevtushenko, A. Lebedev, and A. Das. Nondeterministic State Machines in Protocol Conformance Testing. In Proceedings of the IFIP TC6/WG6.1 Sixth International Workshop on Protocol Test systems VI, pages 363–378, 1994.
[11] M. Yannakakis and D. Lee. Testing finite state machines: fault detection. In Selected papers of the 23rd annual ACM symposium on Theory of computing, pages 209–227, 1995.
Független hivatkozások listája.
[R1] A. Simão and A. Petrenko: Fault coverage-driven incremental test generation. In
Computer Journal Volume 53, Issue 9, November 2010, pp. 1508–1522
[R2] A. Simão and A. Petrenko: Incremental Test Generation Guided by Fault Coverage:
Technical Report. http://www.crim.ca/Publications/ 2009/ documents/ plein_texte/
ASD_SimA_al_0903-01.pdf . ISBN-13 : 978-2-89522-116-6. ISBN-10 : 2-89522-116-
2. 2009.
[R3] E. Uzuncaova, S. Khurshid, and D. Batory: Incremental Test Generation for
Software Product Lines. In IEEE Transactions on Software Engineering, Volume 36,
Number 3, May/June 2010, pp. 309–322
[R4] E. Uzuncaova: Efficient Specification-based Testing Using Incremental Techniques.
Dissertation. http:// hdl.handle.net/ 2152/ 18266 . 2008.
[R5] H. Luo: On Distributed Multi-Point Concurrent Test System and Its Implementation.
In Social Informatics and Telecommunications Engineering 4: 125–129 (2009)
