Doctoral School of Informatics 

BME, Department of Telecommunications and Media Informatics

Supervisor: Zoltán Pap PhD

Incremental Test Generation Algorithms 

Introducing the research area

When developing a new hardware or software, it is inevitable to test the new product very carefully. My research focuses on developing new algorithms which can maintain the test suite of a system described with a formal model in response to changes. The proposed methods utilize the test suite of the previous version of the system and are therefore, more efficient in creating the new test suite than the traditional solutions.

Brief introduction of research place

My research is supported by the Department of Telecommunications and Media Informatics and the High Speed Networks Laboratory (HSNLab) of the Budapest University of Technology and Economics. Both institutions are in close cooperation with the Department of Networked Systems and Services of BME, the Communication Networks Laboratory  (CNL) of the Eötvös Loránd University and with the industrial partner Ericsson.

History and context of the research

Testing plays a very important role in software and hardware development. Large, complex systems continuously evolve to incorporate new features and new requirements. In each evolution step it may also be necessary to modify the testing infrastructure. Manual modification is an ad hoc process that should be avoided, and automatic specification-based test generation methods should be applied instead.

Although automatic test generation methods have been extensively studied in the last few decades [1][2][3], very little effort has been focused on dynamic scenarios involving changing system specifications.

The big majority of test generation algorithms assume rigid, unchanging specifications, they are the so called batch algorithms. A batch test generation algorithm is an algorithm that computes the required output f(y) (the test suite) on some input y (the specification of the system) without assuming any previous results. If an input specification y has been changed into y’, it generates the new output f(y’) (the test suite) from scratch, no matter how small the change has been – see Figure 1. This approach is therefore very inefficient in case of small changes.

 

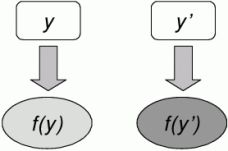
Figure 1: Batch algorithm

 

An incremental algorithm, however, assumes that the same problem has already been solved on a slightly different input. An incremental test generation algorithm uses the previous specification input y, along with the changes dy applied on specification y and the previous test suite f(y) to generate the new test suite f(y’) = f(y + dy) – see Figure 2. This approach may result in significantly faster test generation under most iterative development scenarios.

 

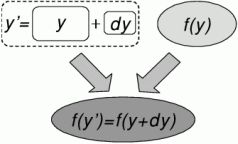
Figure 2: Incremental algorithm

The research goal, open questions

The goal of the research was to develop incremental test generation algorithms which produce test suites with structure and fault detection capability similar to those of batch algorithms. The complexity of these algorithms would only depend on the extent of changes, rather than on the size of specification, thus they would provide an efficient solution for test generation for and testing of continuously evolving systems.

Beside the formal description and implementation of the incremental test generation algorithms, analytical complexity calculations are also essential to investigate how their running time depend on the extent of changes and how they perform compared to the batch test generation algorithms.

Another goal was to create extensive simulations in order to investigate how the running time of the incremental test generation algorithms depend on different input parameters (like different numbers and types of changes, number of states, number of input and output symbols in the specification machine). The following output parameters were taken into consideration: the size of the area affected by changes in respect to the test suite, the gain from incremental algorithms compared to batch methods.

It is important to emphasize, that at the beginning of the research, only one article had dealt with the problem of incremental test generation [4]. This work, however, is not a true incremental algorithm in the sense that it uses traditional batch algorithms to generate test cases for the updated specification, thus its complexity depends on the size of the specification and not on the extent of changes [C1].

Methods

A widely used automatic testing method is the Finite State Machine (FSM) model based conformance testing. The structure of FSM model-based conformance testing is shown in Figure 3. The specification machine M can be considered a white-box with a known internal structure. The developed system Impl is considered a black-box with an unknown internal structure: we can only observe its output responses upon given inputs. Then a test suite is applied to the System Under Test (SUT) Impl and the tester checks whether the observed output sequences of Impl are equivalent to the expected results derived from machine M. This type of testing problem is called conformance testing. The aim of conformance testing is to decide whether the implementation machine Impl correctly implements or conforms to the specification machine M.

 

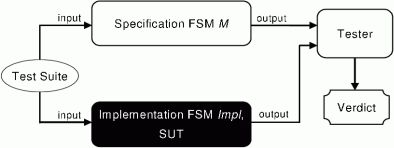
 Figure 3: Finite State Machine model based conformance testing 

 

Many algorithms have been introduced to solve the FSM model based black-box conformance testing, each one with different size of test suite and fault coverage capability.

One such solution is the Transition Tour (TT) method [5], which generates a test suite for strongly connected deterministic FSMs. The test suite generated by the TT-method contains a single test sequence that traverses all transitions and states of the FSM and has a minimal length [6]. The problem of generating a TT test sequence of a specification FSM is based on the Chinese Postman Problem [7] in graph theory where the objective is to find a minimum cost walk that covers each edge of the given graph G at least once and return to the start node.

Another well known solution is the W/Wp/HIS-method triple [8][9][10][11]. These methods guarantee that all output and next state faults will be found if some well defined assumptions about the specification machine hold (strongly connected deterministic reduced specification FSM with reliable reset capability). The test suite of the W/Wp/HIS-method triple – in contrast to the TT-method – is structured: it contains different phases.

The first – state identification – part checks for each state of the specification whether it exists in the implementation as well. The second – transition testing – part checks all remaining transitions of the implementation by observing if the output and the next state conforms to the specification. In the research, the HIS-method [10][11] was put into focus being the most general approach of the three.

Results

I have proposed two incremental test generation algorithms which are based on the traditional batch TT and HIS methods. Incremental algorithms maintain the test cases of these methods to create the test suite efficiently for the changed specification. The various assumptions about specification machines and differences in test cases (size of the entire test suite vs. fault coverage) provide good scalability to the test engineer.

The incremental HIS method guarantees that all output and next state faults will be found if some well specified assumptions about the specification machine hold (strongly connected deterministic reduced specification FSM with reliable reset capability). The method contains two parts which can be used together or independently based on the testing purpose. The two parts together generate a complete test suite. The first part generates test cases to provide state reachability (this part can also be used to check whether the strongly connectedness holds after changes) and the second part generates test cases for state identification (this part can be also used to check whether the machine is reduced).

The incremental TT-method requires much less assumptions about the specification FSM and can handle much more types of changes. Another benefit of the incremental TT-method is that it generates a much smaller test suite than the incremental-HIS does. The test sequence of the incremental TT-method provides 100% transition and 100% state coverage, although it only guarantees to find output faults, thus it has less fault coverage, than incremental-HIS has.

The incremental algorithms have been described formally in conference and journal papers [C1][J2], and they have been also implemented. The efficiency of the proposed algorithms has been compared to the traditional HIS and TT method both via analytical complexity calculations and comprehensive empirical analyses [C1][C6][J2]. Complexity calculations show that the complexity of the algorithm depends only on the extent of changes, rather than the size of the specification itself. In the worst case situation – when the changes affect the entire system – the complexity of incremental algorithms is the same as that of the batch algorithms. In most iterative development scenarios, however, the changes affect only a small portion of the system. In these cases the incremental algorithms generate the test cases for the updated system much more efficiently than the traditional batch algorithms. To investigate the gain of the incremental algorithms compared to their batch counterparts I performed extensive simulations. The simulations indicate that incremental test generation algorithms are much more efficient even in case of extensive changes. The investigations also show that the gain of incremental algorithms compared to batch algorithms are increasing if the size of specification is growing.

 

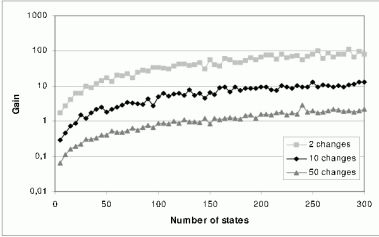
Figure 4: The gain of the first part of the incremental HIS algorithm compared to the corresponding part of the batch HIS-method

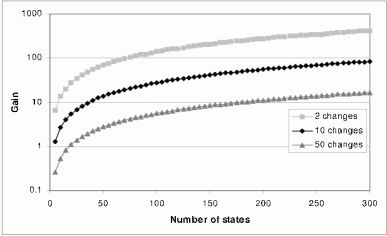
Figure 5: The gain of the second part of the incremental HIS algorithm compared to the corresponding part of the batch HIS-method

 

Figures 4 and 5 show the gain of the first and the second part of the proposed incremental HIS algorithm compared to the corresponding part of the batch HIS-method, respectively, as a function of number of states in the specification in case of 2, 10 and 50 changes (the number of state transitions in the simulation is 5 instances/state).

 

Figure 6: The gain of incremental TT algorithm compared to the corresponding part of the batch TT-method

 

Figure 6 shows the gain of the proposed incremental TT algorithm compared to the batch TT-method as a function of the number of states in the specification FSM (average number of state transitions in the simulation is 5 instances/state).

Expected impact and further research

The article covering the incremental HIS algorithm [C1] has been independently cited by international experts in relevant conference proceedings, journals and a dissertation [R1]-[R5].

An article covering the TT algorithm [J2] has been published this year, where citations are yet to be expected.

The goals set at the beginning of the doctoral studies have been achieved.

A possible future investigation is to extend the proposed algorithms to other problems and models. For instance, the algorithms could be modified to deal with extended finite state machines. The incremental-TT algorithm can be also extended to other, non finite state machine-based models. Another interesting future task would be to integrate the incremental test generation algorithms into real test frameworks and to use the feedback of this work to refine the proposed algorithms based on actual needs further. Such an application could be an automatic software testing during development phases.

Own publications, references, links

Related own publications 

[J1] G. Kovács, G. Á. Németh, Z. Pap, and M. Subramaniam: Deriving compact test

suites for telecommunication software using distance metrics. In Journal of Communications Software and Systems, Volume: 5 Number: 2

[J2] G. Á. Németh and Z. Pap: Incremental Maintenance of Transition Tour. In Fundamenta Informaticae, Volume: 129 Number: 3

[B1] G. Á. Németh: Protocol Operation. In Advanced Communication Protocol Technologies: Solutions, Methods and Applications. Hershey; New York: IGI Global, Information Science Reference, 2011. pp. 20–37.

[B2] G. Kovács, G. Á. Németh and Z. Pap: Convergence of fix and mobile networks. In Advanced Communication Protocol Technologies: Solutions, Methods and Applications. Hershey; New York: IGI Global, Information Science Reference, 2011. pp. 226–246. Lecture

[C1] Z. Pap, M. Subramaniam, G. Kovács and G. Á. Németh: A Bounded Incremental Test Generation Algorithm for Finite State Machines. In Proc., Testcom/Fates 2007, Tallinn, Estonia, June 2007.

[C2] G. Kovács, G. Á. Németh, Mahadevan Subramaniam and Zoltán Pap: Optimal String Edit Distance Based Test Suite Reduction for SDL Specifications. In Proc., SDL 2009, Bochum, Germany, September 2009.

[C3] G. Adamis, A. Wu-Hen-Chang, G. Á. Németh, L. Erős, G. Kovács: Data Flow Testing in TTCN-3 with a Relational Database Schema. In Proc., SDL 2013, Montreal, Canada, June 2013.

[C4] G. Kovács, G. Á. Németh, Z. Pap, and M. Subramaniam: Deriving compact test suites for telecommunication software using distance metrics. In Proc., SoftCOM 2008, Split-Dubrovnik, Croatia, September 2008.

[C5] G. Németh and G. Á. Németh: A Generic Model for Advanced Networks Handling Imprecise Information. In Proc., SoftCOM 2009, Hvar, Croatia, September 2009.

[C6] G. Á. Németh, Z. Pap and G. Kovács: The Incremental Maintenance of a Checking Sequence. In Proc., AACS’13, Budapest, Hungary, June 2013.

[C7] G. Á. Németh and Z. Pap: Inkrementális tesztgenerálás (in Hungarian). In Tavaszi Szél 2012,

Győr, Hungary, 2012.

 

Publication list

 

References

[1] M. Broy, B. Jonsson, J.-P. Katoen, M. Leucker and A. Pretschner (Eds.), Model-Based Testing of Reactive Systems (Springer-Verlag, New York, 2005).

[2] R. Dorofeeva, K. El-Fakih, S. Maag, A. R. Cavalli, N. Yevtushenko, Fsm-based conformance testing methods: A survey annotated with experimental evaluation, Information and Software Technology 52(12) (2010): 1286–1297.

[3] D. Lee and M. Yannakakis. Principles and Methods of Testing Finite State Machines – A Survey. Proceedings of the IEEE, 84(8):1090–1123, 1996.

[4] Rita Dorofeeva, Khaled El-Fakih, Stephane Maag, Ana R. Cavalli, and Nina Yevtushenko. FSM-based conformance testing methods: A survey annotated with experimental evaluation. Information and Software Technology, 52(12):1286– 1297.

[5] S. Naito, M. Tsunoyama. Fault detection for sequential machines by transition-tours. in Proceedings of the 11th IEEE Fault-Tolerant Computing Conference (1981): 238–243.

[6] Mark Utting, Bruno Legeard. Practical Model-Based Testing: A Tools Approach. Morgan Kaufmann Publishers Inc., San Francisco, CA, USA, 2007.

[7] Jack Edmonds and Ellis L. Johnson. Matching, Euler tours and the Chinese postman. Mathematical Programming (1973) 5(1): 88–124.

[8] T. Chow. Testing software design modelled by finite-state machines. IEEE Transactions on Software Engineering, 4(3):178–187, May 1978.

[9] S. Fujiwara, G. v. Bochmann, F. Khendec, M. Amalou, and A. Ghedamsi. Test selection based on finite state model. IEEE Transactions on Software Engineering, 17(6):591–603, 1991.

[10] A. Petrenko, N. Yevtushenko, A. Lebedev, and A. Das. Nondeterministic State Machines in Protocol Conformance Testing. In Proceedings of the IFIP TC6/WG6.1 Sixth International Workshop on Protocol Test systems VI, pages 363–378, 1994.

[11] M. Yannakakis and D. Lee. Testing finite state machines: fault detection. In Selected papers of the 23rd annual ACM symposium on Theory of computing, pages 209–227, 1995.

 

Independent citations

[R1] A. Simão and A. Petrenko: Fault coverage-driven incremental test generation. In

Computer Journal Volume 53, Issue 9, November 2010, pp. 1508–1522

[R2] A. Simão and A. Petrenko: Incremental Test Generation Guided by Fault Coverage:

Technical Report. http://www.crim.ca/Publications/ 2009/ documents/ plein_texte/

ASD_SimA_al_0903-01.pdf . ISBN-13 : 978-2-89522-116-6. ISBN-10 : 2-89522-116-

2. 2009.

[R3] E. Uzuncaova, S. Khurshid, and D. Batory: Incremental Test Generation for

Software Product Lines. In IEEE Transactions on Software Engineering, Volume 36,

Number 3, May/June 2010, pp. 309–322

[R4] E. Uzuncaova: Efficient Specification-based Testing Using Incremental Techniques.

Dissertation. http:// hdl.handle.net/ 2152/ 18266 . 2008.

[R5] H. Luo: On Distributed Multi-Point Concurrent Test System and Its Implementation.

In Social Informatics and Telecommunications Engineering 4: 125–129 (2009)