 |
BMe Kutatói pályázat |

|
BME Informatikai Tudományok Doktori Iskola
BME VIK, Híradástechnikai
Tanszék (HIT)
Témavezető: Dr. Imre Sándor
Klasszikus
és kvantum-információ kódolása extrém zajos
környezetben
Kidolgoztam
egy kvantum-csatornakódolási eljárást, amellyel extrém zajos, kiindulási
állapotban információtovábbításra alkalmatlan kvantumcsatornákon keresztül is
megvalósítható az információátvitel. A módszer segítségével a kvantumcsatornák
kapacitás-visszaállíthatósága az eddigi kódolási módszerek esetében fennálló
kötöttségek és speciális peremfeltételek nélkül is
megvalósítható.
A kutatóhely
rövid bemutatása
A BME
Híradástechnikai Tanszék 1991-ben alakult. A tanszék oktatási és kutatási
feladatai szorosan kapcsolódnak a híradástechnika módszereihez és a hírközlő
rendszerek tervezéséhez, az elektronikához és a számítástechnikához. A tanszék
aktív szerepet vállal a Kar alap, mester és doktori szintű képzésében mind a
villamosmérnöki, mind pedig a műszaki informatika szakon.
A kutatás
történetének, tágabb kontextusának bemutatása
A Moore-törvény alapján, 2020-ra várhatóan egy bit információt egy atom tárol
majd, így már néhány éven belül elérkezhet a kvantuminformatika világa. A
kvantumszámítógép működése a kvantumelméletre épül, és alkalmas arra, hogy
minden mai modern, feltörhetetlennek vélt kódot másodpercek alatt feltörjön. A
kvantumszámítógépek napjainkban ugyan még nem állnak rendelkezésre, ellenük
azonban csak a kvantumcsatornákon keresztüli kommunikáció nyújthat abszolút
védelmet. A jövőbeni védelmi módszerek kidolgozása szempontjából így már ma
alapvető fontosságú a kvantumcsatornákon keresztüli kommunikáció lehetőségeinek
pontos megismerése. Kutatásaink célja a jövő kvantum-kommunikációs hálózataiban
rejlő lehetőségek feltérképezése és alkalmazhatóságának vizsgálata.
A kutatási munka keretén belül vizsgáltuk a zajos kvantumcsatornák kapacitás
visszaállíthatóságának kérdését, a nagy-hatótávolságú, biztonságos
kvantum-kommunikáció gyakorlati implementálhatóságát.
Kutatás
eredményeink jelentősége
A
szuperaktiválás segítségével, egyenként zéró kapacitással rendelkező
kvantumcsatornák együttesen akár teljesen hibamentes információátvitelre is
használhatók. A kutatómunka keretében kidolgoztunk egy forradalmian új
kvantum-kódolási eljárást, amellyel a szuperaktiválással egyenértékű eredmények
érhetőek el. A módszerünk előnye, hogy a kvantumcsatornák kapacitás-visszaállíthatósága a szuperaktiválás jelenségének eléréséhez szükséges
kötöttségek és speciális peremfeltételek nélkül is megvalósítható. A módszerünk
- összehasonlítva a hagyományos szuperaktiválással - nagyságrendekkel hatékonyabb
megoldást nyújt a kvantumcsatornák kapacitásának visszaállítására és
erősítésére. A kidolgozott eljárásunk neve poláraktiválás.
A
poláraktiválás egy speciális kódolási eljárásra, az ún. polár-kódolásra épül. A
poláraktiválás segítségével a szuperaktiválással azonos eredmények érhetőek el –
kiindulási állapotban extrém zajos, információátvitelre alkalmatlan
kvantumcsatornák használhatóak értékes információ átvitelére. A módszer
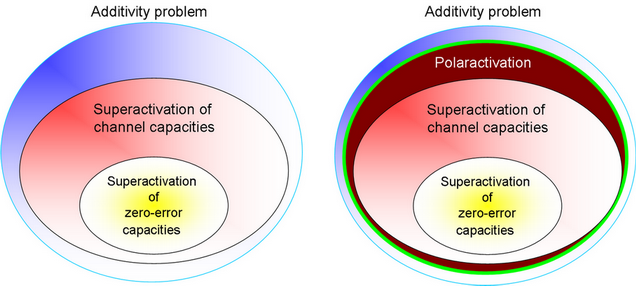
általánosabb megoldást jelent a szuperaktiválásnál (1. ábra).
Mind
a szuperaktiválás, mind pedig a poláraktiválás alapját az ún.
„additivitási-tétel” sérülése jelenti: két kvantumcsatorna kombinálásával, és
azok együttes használatával több információ továbbítható, mint a két független
csatornán átküldött információmennyiség összege. A szuperaktiválás és
poláraktiválás az additivitási tétel extrém sérülése: a kombinált
csatornamodellben található csatornák önmagukban nem képesek
információátvitelre; - a kombinált struktúra kapacitása azonban mégis pozitívvá
tehető.
A
szuperaktiválásban rejlő lehetőségek forradalmiak. A kutatási munkánkban kiemelt
fontosságot kapott a szuperaktiválási lehetőségek kutatása, feltérképezése és
alkalmazhatósági lehetőségeinek vizsgálata a jövő telekommunikációs
hálózataiban, - elsődlegesen kiemelve az optikai-alapú, valamint vezeték nélküli
kvantum-kommunikációs hálózatokat. A szuperaktiválás jelensége ugyanakkor számos
peremfeltételhez kötött.

A kutatás célja
Célunk a
szuperaktiválás jelenségénél fennálló peremfeltételek és kötöttségek
eliminálása: definiáltuk a
poláraktiválás fogalmát, valamint bizonyítottuk annak matematikai hátterét és
igazoltuk annak információelméleti helyességét.
A kutatómunka
keretén belül kidolgoztunk egy forradalmian új kvantum-kódolási eljárást,
amellyel a szuperaktiválással egyenértékű eredmények érhetőek el. A módszerünk
előnye, hogy a kvantumcsatornák kapacitás-visszaállíthatósága a szuperaktiválás
jelenségének eléréséhez szükséges kötöttségek és speciális peremfeltételek
nélkül is megvalósítható. Módszerünk - összehasonlítva a hagyományos
szuperaktiválással -
nagyságrendekkel hatékonyabb megoldást nyújt a kvantumcsatornák
kapacitásának visszaállítására és erősítésére (3. ábra).
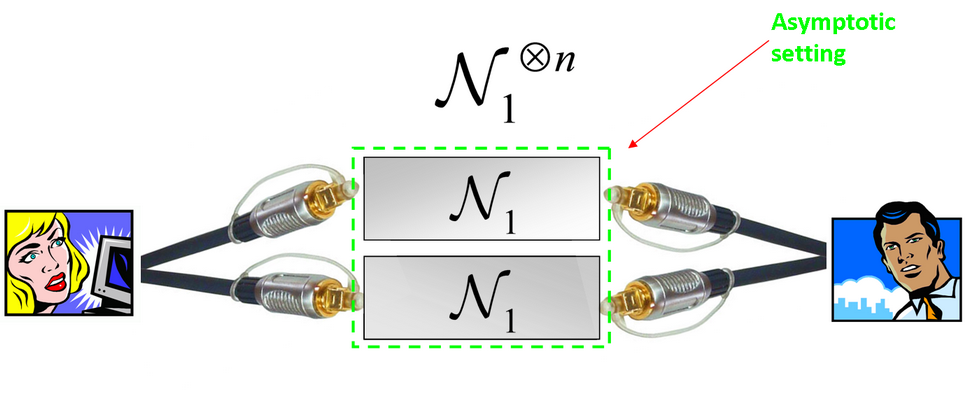
Kvantumcsatornák
poláraktiválása
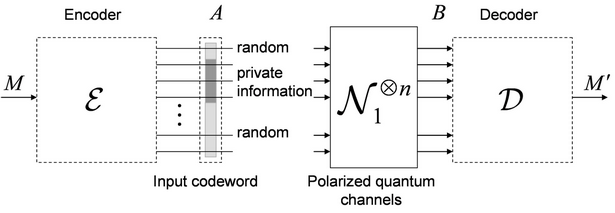
A poláraktiválás
segítségével tetszőleges, zéró kommunikációs
kapacitással rendelkező kvantumcsatornák használhatók információátvitelre, a
módszer pedig – a gyakorlati megvalósítás szempontjából releváns - optikai
kvantumcsatorna-modellek esetében is alkalmazható. A módszer a
csatornapolarizáció jelenségére épül: az alkalmazott csatornakódolási módszernek
köszönhetően a bemeneti kódszó bitjeit két különböző csatornatípus továbbítja.
Az egyik halmazban a közel teljesen zajmentes csatornák találhatók, míg a másik
halmaz elemei az információátvitelre alkalmatlan kvantumcsatornák (4. ábra).
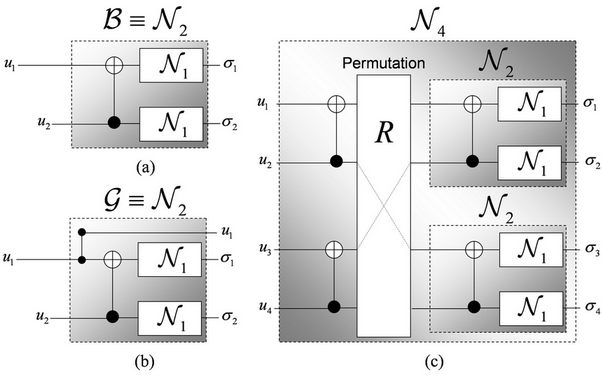
A munka keretében kidolgoztuk a poláraktiválás jelenségének eléréséhez szükséges matematikai
hátteret, igazoltuk annak információelméleti helyességét, valamint bizonyítottuk
a kidolgozott módszerünk hatékonyságát és alkalmazhatóságát. A módszert
kiterjesztettem a klasszikus privát kapacitás poláraktiválására, amely eredmény
szuperaktiválás segítségével nem érhető el (5. ábra).
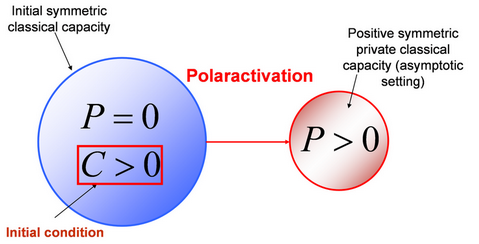
Eredmények
Megadtuk a
poláraktiválás eléréséhez szükséges csatornakódolási eljárást is, valamint
javaslatot tettünk annak alkalmazhatóságára a jövő telekommunikációs
rendszereiben.
A kutatásaimban
mind a klasszikus, mind pedig a kvantum információátvitel poláraktiválási
lehetőségeit elemeztem, kiemelve a kvantumcsatornák hibamentes, klasszikus- és
kvantum-kapacitásának vizsgálatát.
A kutatási munka
keretén belül javaslatot tettem a napjainkban ismert kvantum-repeaterek működési
mechanizmusának, illetve azok strukturális felépítésének módosításaira, amely
módosításnak köszönhetően nagyságrendekkel hatékonyabb kommunikáció valósítható
meg a jövő kvantum-kommunikációs hálózataiban.
A jövő
telekommunikációs rendszereinek szempontjából kiemelt fontosságú a privát
információtartalom átküldésének lehetősége. Megmutattam, hogy a kvantumcsatornák
privát kapacitása is poláraktiválható (6. ábra), amely eredmény mind a
kvantum-kriptográfia alapú, mind pedig a kvantum-telekommunikációs hálózatokban
felhasználható.
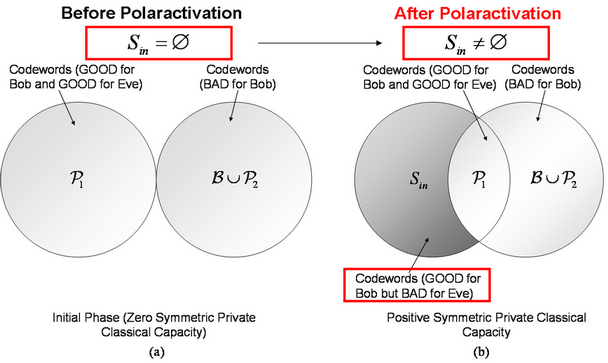
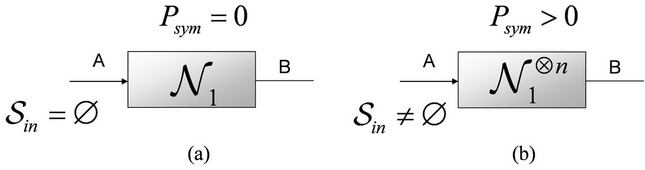
6. ábra. (a): A kvantumcsatornák
poláraktiválása előtt a csatornák nem képesek privát információ átvitelére. (b):
A poláraktiválást követően a csatornák képesek a privát kommunikáció átvitelére
is, amelyet a bemeneti kódszóhalmaz átrendeződése reprezentál
(b).
Meghatároztam a
privát kapacitás poláraktiválásához szükséges feltételrendszert, valamint a
bemeneti kódszavak tulajdonságait. Több különböző kódszó halmazt definiáltam,
valamint meghatároztam az elérthető poláraktivált csatornakapacitást a
konstruált kódszavak jellemzőinek függvényében. A Bhattacharya paraméter a
kvantumcsatorna zaját jellemzi: 0 egy zajmentes csatorna esetén, 1 maximális zaj
esetén.
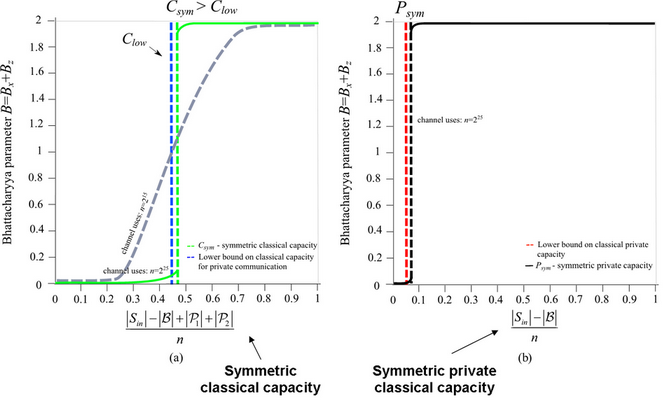
7.
ábra. (a): A
csatornapolarizáció következtében kialakuló halmazok csatornaindexeinek aránya a
kvantumcsatorna poláraktivált kapacitásával egyenlő. (b): Meghatároztam a privát
kapacitás poláraktiválásához szükséges alsó kapacitáskorlátot. A kritikus alsó
korlát elérését követően a poláraktivált csatornákon keresztül privát
kommunikáció valósítható meg.
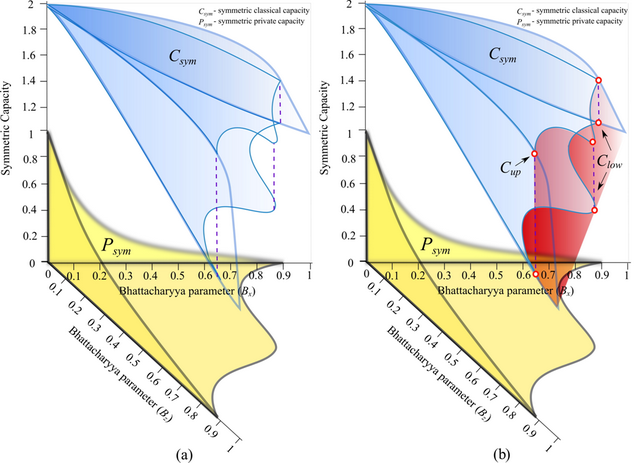
8. ábra. (a): A poláraktiválás előtt a csatorna nem képes privát információ átvitelére. (Jelölések: sárga tartomány: privát kapacitás, kék tartomány: pozitív klasszikus kapacitás és pozitív privát kapacitás, vörös tartomány: pozitív klasszikus kapacitás és zéró privát kapacitás. A csatorna kiindulási állapotban vörös tartománnyal jellemezhető.). (b): A poláraktiválás hatására a csatorna privát kapacitása pozitív lesz, így a kezdetben zéró privát kapacitással rendelkező csatorna is alkalmassá tehető privát információ átvitelére (a poláraktiválás hatására a kék tartományba átlépve, pozitív privát kapacitás realizálható).
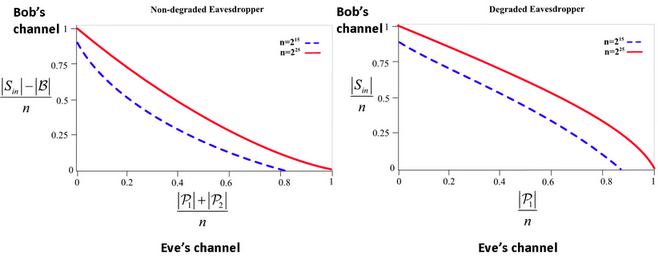
9. ábra. (a): A poláraktiválás különböző tulajdonságú kvantumcsatornákra is kiterjeszthető. A lehallgató kvantumcsatornának minőségétől függően megkülönböztethetjük a nem-degradált (a lehallgató csatornája jó minőségű), (b): illetve degradált (a lehallgató csatornája rossz minőségű) kvantumcsatornákat.
Poláraktiválás
hatékonysága
A poláraktiválás
hatékonyságát a kódolási metódusban alkalmazott polár kódszavak garantálják. Az
adott kvantumcsatorna n használatát
feltételezve, a módszer komplexitása
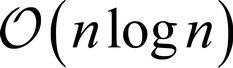
Összefoglalás
A poláraktiválás
számos előnnyel rendelkezik a hagyományos szuperaktiváláshoz képest.
Amíg a szuperaktiválás jelensége számos kiinduló feltételhez és peremfeltétekhez
kötött, addig a poláraktiválás tetszőleges kvantumcsatornára alkalmazható.
Klasszikus kommunikáció zéró-kapacitású
kvantumcsatornákon keresztül
A
kvantumcsatornák kapacitás-visszaállításának kérdését kiterjesztettük a
kvantumcsatornák klasszikus
kapacitására, amely jelentős elméleti
áttörést jelent a kvantumcsatornákon keresztüli információátvitel valódi
információelméleti háttérének megismerése szempontjából.
Kidolgoztuk a
zéró-kapacitású kvantumcsatornákon keresztüli klasszikus információátvitel
megvalósításához szükséges elméleti modellt és igazoltuk annak
információelméleti helyességét.
Felfedezésünk
jelentősége
A szuperaktiválás
jelenségét a kvantumcsatornák kvantum-kapacitásra igazolták. A klasszikus kapacitás szuperaktiválása
lehetetlennek bizonyult. A kutatási munka keretén belül beláttuk, hogy a
szuperaktiválási jelensége a klasszikus információátvitelre is kiterjeszthető,
amely jelentős matematikai és információelméleti következményeket von maga után.
A bevezetett módszerünk neve „kvázi-szuperaktiválás”, ugyanis a
szuperaktiválással egyenértékű eredményeket, a hagyományos értelemben vett
szuperaktiválástól eltérő megoldások segítségével értük el.
A csatornamodell
elemei a következő ábrán láthatóak. Az első csatorna tetszőleges,
zéró-kapacitású kvantumcsatorna lehet. A második csatorna az ún. „cloning”-csatorna, amely a stimulált
emisszió fizikai folyamatát modellezi (12. ábra).
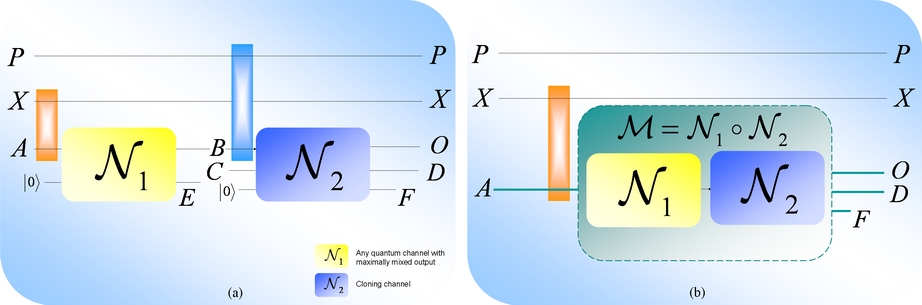
Az M csatorna klasszikus kapacitása zéró,
ugyanis a csatorna O kimenete és
Alice X regisztere között minden
klasszikus korreláció megszűnik. A pozitív klasszikus kapacitás elérésének
feltétele az X bemeneti regiszter és
a csatorna kimenet közötti klasszikus korreláció visszaállítása. Amíg egyetlen
M csatorna esetében a klasszikus
korreláció visszaállítására nincs mód, két M csatorna, valamint egy speciális
kiegészítő összefonódott állapot használatával visszaállítható az X regiszter és a csatornakimenetek közti
korreláció (13. ábra). A hagyományos értelemben vett szuperaktiválással ezen
eredmény nem érhető el, ugyanis két, egyenként zéró klasszikus kapacitással
rendelkező kvantumcsatorna nem szuperaktiválható – amely matematikailag is
belátható a Choi-Jamiolkowski tételek
segítségével.
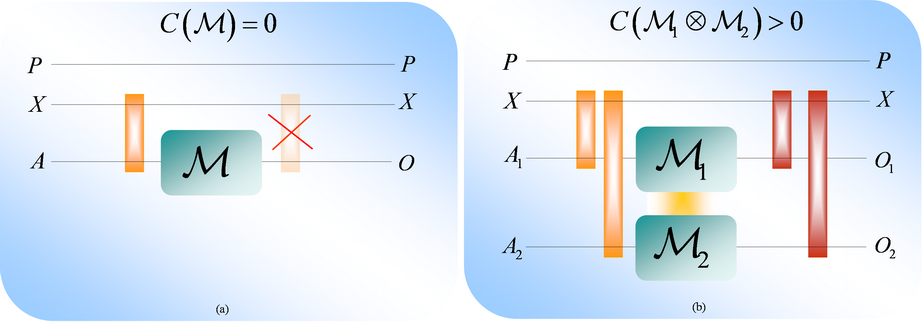
13. ábra. (a): Az M kvantumcsatorna klasszikus kapacitása zéró: a csatorna megsemmisít minden klasszikus korrelációt az X bemeneti regiszter valamint az O csatorna kimenet között. (b): két csatorna együttes alkalmazásával, valamint megfelelő mennyiségű összefonódottságot tartalmazó kiegészítő bemenet esetén klasszikus korreláció állítható elő a kombinált csatornastruktúra kimenetei, valamint az X bemeneti regiszter között.
A
„kvázi-szuperaktiválás” segítségével klasszikus kommunikáció is megvalósítható egyenként zéró klasszikus kapacitással rendelkező csatornák esetén. A két,
egyenként zéró-kapacitással rendelkező csatorna együttes alkalmazásával pozitív
kapacitás érhető el. A bemeneti X
regiszter és a kombinált csatornastruktúra kimenetei között klasszikus
korreláció jelenik meg, amely a pozitív klasszikus kapacitás feltétele. A
nem-zérus klasszikus kapacitás azonban csak a két csatorna együttes
használatával, valamint egy speciális kiegészítő bemenet használatával érhető
el. A kiegészítő bemenet teljesen független a kvantumcsatornák tényleges
bemenetétől (14. ábra).
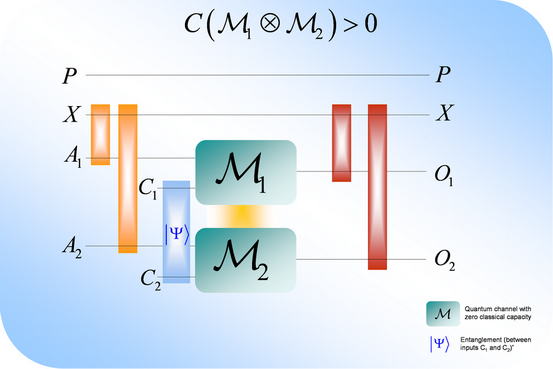
14. ábra. A kvázi-szuperaktiválás jelenségének összefoglalása. A kombinált csatornastruktúra kimenetei és a klasszikus X regiszter közötti klasszikus korreláció megteremtése csak egy speciálisan megválasztott, összefonódott kiegészítő állapot segítségével lehetséges. A kiegészítő bemeneti állapotban kódolt speciális mértékű összefonódottság aktiválja a két, információátvitelre önmagában teljességgel alkalmatlan kvantumcsatornát. A kiegészítő bemeneti állapot teljesen független a csatornabemenetektől valamint az X klasszikus regisztertől, azonban az állapotból értékes információ nyerhető ki.
A jelenség
előidézésének előfeltétele a kiegészítő bemenet megfelelő megválasztása.
Bebizonyítottam, hogy az X regiszter
és a csatornakimenetek közti klasszikus korreláció csak és kizárólag
összefonódott kiegészítő bemenetek alkalmazásával valósítható meg, ugyanakkor
ezen összefonódottság nem lehet maximális. A kiegészítő bemenetben kódolt
összefonódottság mértéke csak egy jól specifikált tartományon belül mozoghat. Az
összefonódottság mértéke egyúttal a visszaállítható klasszikus korreláció
mértékét is meghatározza (15. ábra).
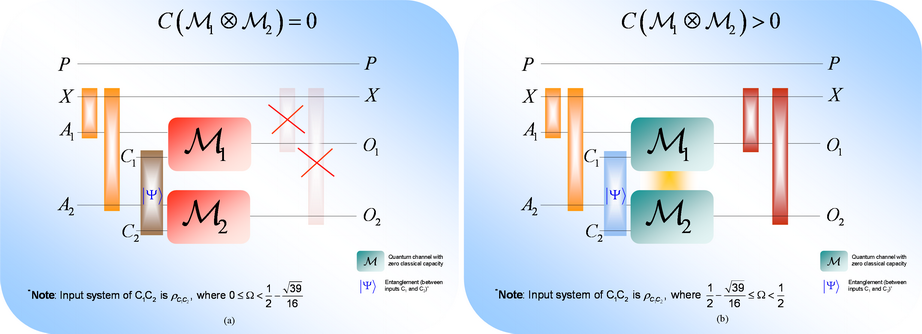
15. ábra. (a): Amennyiben a kiegészítő bemenetben kódolt összefonódottság mértéke egy speciális tartományon kívül található, a két csatorna nem képes aktiválni egymást, a kombinált struktúra kapacitása pedig triviálisan zéró. (b) Speciálisan megválasztott összefonódottság esetén a két csatorna aktiválja egymást. A kiegészítő állapotban kódolt összefonódottság felhasználható a csatornakimenetek és az X regiszter közötti klasszikus korreláció visszaállítására. A kiegészítő bemenet független mind az X regisztertől, mind pedig az A bemeneti rendszertől.
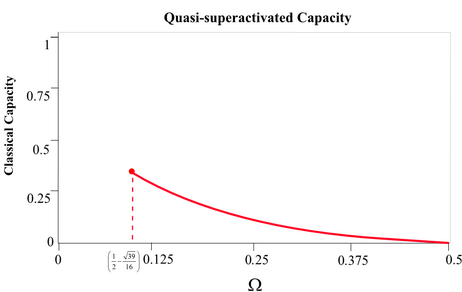
Megállapítottam,
hogy a zéró kapacitású kvantumcsatornákat tartalmazó
csatornastruktúra kimenetei, valamint az X bemeneti regiszter között
visszaállított klasszikus korreláció alapján, a csatornastruktúra klasszikus
kapacitása a következőképpen fejezhető ki (16. ábra). (Omega - a kiegészítő
bemeneti állapotban kódolt összefonódottság mértéke, 0,5 esetén
maximális).
Fejlett
kvantum-hibajavítás vezeték nélküli és satellite kvantumcsatornákhoz
A poláraktiválás és a kvázi-szuperaktiválás mellett kidolgoztam egy hatékony, minimális redundanciára épülő kvantum-hibajavító protokollt. A protokoll nagy hatékonysággal alkalmazható vezeték nélküli, valamint satellite-alapú rendszerek esetén. A kifejlesztett hibajavító metódus - szemben az eddigiekben alkalmazott kvantum-hibajavító algoritmusokkal – ismeretlen kvantumállapotokban kódolja a kvantumcsatorna ismeretlen zaj transzformációját. A kvantumállapotok a hibajavítási folyamatban egy inverz transzformációt követően felhasználhatók az ismeretlen kvantumállapotokon bekövetkezett – szintén ismeretlen – hiba javítására. Az ismeretlen d kvantumállapot javítására a szintén ismeretlen teta kvantumállapotokkal kerül sor, amely állapotok a kvantumcsatorna ismeretlen zaj-transzformációját kódolják (17. ábra).
Az eredmény
jelentősége
A
hibajavítás tetszőleges méretű kvantum-kódszóra kiterjeszthető – az aktuális
kvantumcsatorna fizikai paramétereinek függvényében. Az általam kidolgozott módszer
teljességgel szakít a hagyományos kvantum-hibajavítási módszerek esetén
alkalmazott eljárásokkal. A módszer hatékonysága nagyságrendekkel meghaladja a
jelenlegi metódusok hatékonyságát. Kidolgoztam a módszer információelméleti és
matematikai bizonyítását, ugyanakkor a tényleges potenciál kihasználásához,
valamint a fizikai megvalósítások jellemzőinek feltérképezéséhez laboratóriumi
tesztelések szükségesek a későbbiekben.
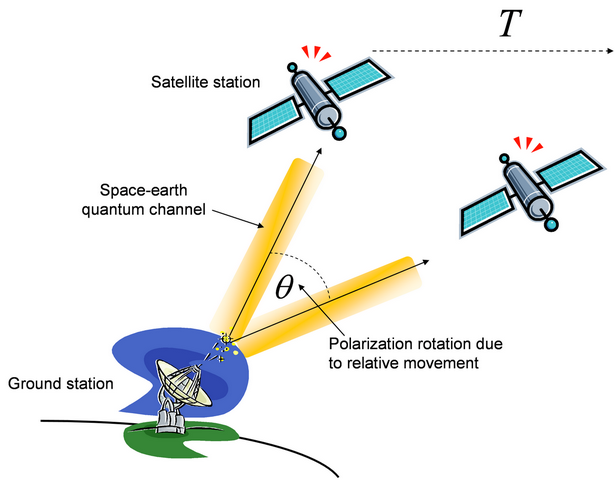
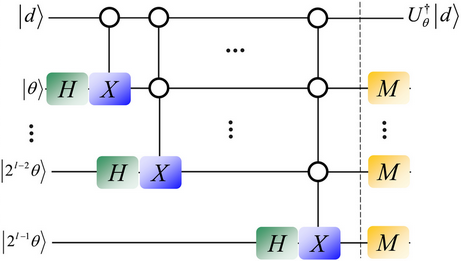
A kifejlesztett
kvantum-hibajavító módszerem az első NASA kvantum-konferencián (First NASA
Quantum Future Technologies Conference, NASA Ames Research Center, Moffett Field,
California, USA.), valamint egy szakmai konferencián is bemutattam (Second International Conference on Quantum
Error Correction (QEC11), Dec. 2011, University of Southern California, Los
Angeles, USA).
Összefoglaló
A
kvantumcsatornák kapacitásának visszaállítása - klasszikus kommunikációs
rendszerekben nem megvalósítható, tisztán kvantummechanikai jelenségekre épül -
új távlatokat nyitva a jövő telekommunikációs hálózatainak kommunikációjában. A
szuperaktiválás segítségével, egyenként zéró kapacitással rendelkező
kvantumcsatornák együttesen, akár teljesen hibamentes információátvitelre is
használhatók. A poláraktiválásban rejlő lehetőségek
forradalmiak.
A kutatási
munkámban emellett kiemelt fontosságot kapott a szuperaktiválási lehetőségek
kutatása, feltérképezése és alkalmazhatósági lehetőségeinek vizsgálata a jövő
telekommunikációs hálózataiban - elsődlegesen az optikai-alapú,
valamint vezeték nélküli kvantum-kommunikációs hálózatokat tanulmányozva. A kidolgozott
csatornakódolási eljárások segítségével átléphetőek a jelenleg ismert hibajavító
algoritmusok korlátai. A kidolgozott hibajavító algoritmus nagy hatékonysággal
alkalmazható szabadtéri, illetve üvegszálas optikai kvantumcsatornák esetében,
valamint a kvantum-repeaterek közti kommunikációban.
Köszönetnyilvánítás
A
kutatási eredményeket a TAMOP-4.2.1/B-09/1/KMR-2010-0002, 4.2.2.B-10/1--2010-0009, valamint a COST Action MP1006
támogatta.
Hivatkozások
E.
Arikan. Channel polarization: A method for constructing capacity achieving codes
for symmetric binary-input memoryless channels. IEEE Transactions on Information
Theory, 55(7):3051–3073, July 2009.
arXiv:0807.3917.
H.
Mahdavifar and A. Vardy. Achieving the Secrecy Capacity
of Wiretap Channels Using Polar Codes. arXiv:1001.0210v2 [cs.IT], April 2010.
M.
M. Wilde and S. Guha. Polar codes for classical-quantum channels.
arXiv:1109.2591v1 [quant-ph], September 2011.
K. Bradler, An infinite
sequence of additive channels: the classical capacity of cloning channels. IEEE
Trans. Info. Theory, vol. 57, no. 8, arXiv:0903.1638,
(2011)
K.
Bradler, P. Hayden, D. Touchette, and
M. M. Wilde, Trade-off capacities of the
quantum Hadamard channels, Journal of Mathematical Physics 51, 072201,
arXiv:1001.1732v2, (2010).
A.
Holevo, “The capacity of the quantum channel with general signal states”, IEEE
Trans. Info. Theory 44, 269 - 273 (1998).
B.
Schumacher and M. Westmoreland, “Sending classical information via noisy quantum
channels,” Phys. Rev. A, vol. 56, no. 1, pp. 131–138,
(1997).
S.
Lloyd, “Capacity of the noisy quantum channel,” Phys. Rev. A, vol. 55, pp.
1613–1622, (1997)
P.
Shor, “The quantum channel capacity and coherent information.” lecture notes,
MSRI Workshop on Quantum Computation, Available online at
http://www.msri.org/publications/ln/msri/2002/quantumcrypto/shor/1/.
(2002).
I.
Devetak, “The private classical capacity and quantum capacity of a quantum
channel,” IEEE Trans. Inf. Theory, vol. 51, pp. 44–55, quant-ph/0304127,
(2005).
G.
Smith, J. Yard, Quantum Communication with Zero-capacity Channels. Science 321,
1812-1815 (2008)
G.
Smith, J. A. Smolin and J. Yard, Gaussian bosonic synergy: quantum communication
via realistic channels of zero quantum capacity, arXiv:1102.4580v1, (2011).
R. Duan, Superactivation of zero-error capacity of noisy quantum
channels.arXiv:0906.2527, (2009)
T. S. Cubitt, G. Smith,
Super-Duper-Activation of Quantum Zero-Error Capacities, arXiv:0912.2737v1.
(2010).
T.
Cubitt, D. Leung, W. Matthews and A. Winter, Improving
Zero-Error Classical Communication with Entanglement, Phys. Rev. Lett. 104,
230503 (2010), arXiv:0911.5300 [quant-ph]
T. Cubitt, J. X. Chen, and A.
Harrow, Superactivation of the Asymptotic Zero-Error Classical Capacity of a
Quantum Channel, arXiv: 0906.2547. (2009)
F.G.S.L. Brandao, J. Oppenheim and S. Strelchuk, "When does
noise increase the quantum capacity?", arXiv:1107.4385v1 [quant-ph]
(2011)
M.
Christandl, A. Winter, Uncertainty, Monogamy, and
Locking of Quantum Correlations, IEEE Trans Inf Theory, vol 51, no 9, pp 3159-3165 (2005).,
arXiv:quant-ph/0501090.
Eredmények
Konferenciák
Az eredmények
külföldi konferenciákon kerültek bemutatásra, többek között::
- Massachusetts
Institute of Technology (MIT), (Cambridge, USA)
- Stanford
University (USA)
- First NASA
Quantum Future Technologies Conference (NASA Ames Research Center, Moffett
Field, California, USA.)
- University of
Tokyo (Tokyo, Japan)
- University of
Southern California (Los Angeles, USA)
- University of
Oxford, (United Kingdom)
- University of
Montreal (Canada)
- University of
Cambridge (Cambridge, UK),
- University of
Harvard (Cambridge, USA),
- University of
Berkeley (California, USA),
- Princeton
University (New Jersey, USA),
- University of
Arizona (Arizona, USA);
- University of
Ottawa (Canada)
- University of
Queensland (Australia),
- University of
Southampton (UK),
- National
Institute of Informatics, Tokyo (Japan),
- Nanyang
Technological University, (Singapore).
A szakmai konferenciacikkekkel 2009-ben Future Computing „Best Paper Award” díjat, valamint 2010-ben a Harvard Egyetem (Cambridge, USA) szakmai díját sikerült elnyernem. 2009-ben a Hírközlési és Informatikai Tudományos Egyesület „Pollák-Virág” díját, 2010-ben a Csibi Sándor Ösztöndíjat, valamint az Arizonai Egyetem díját sikerült elnyernem. Kutatási eredményeimmel 2011-ben a Stanford Egyetem, a Dél-Kaliforniai Egyetem, valamint a QIP 2012 (Quantum Information Processing) konferencia díját, míg 2012-ben az APS (American Physical Society, California, USA), valamint az OSA (The Optical Society of America, Rochester, New York, USA) díját nyertem el.
Publikációk
A kutatási eredmények nemzetközi szakmai folyóiratokban kerültek publikálásra (pl. IEEE, Elsevier, Springer, Wiley.)
Proceedings
of the IEEE (Special Centennial Celebration Issue)
Két cikk publikálása a Proceedings of the IEEE folyóirat 100 éves jubileumi különszámában.
100th Year
Anniversary Celebration Volume of the Proceedings
of the IEEE (Special
Centennial Celebration Issue: Reviewing the Past, the Present, and the
Future of Electrical Engineering Technology and the
Profession)
Sandor
Imre, Laszlo Gyongyosi: Introduction to Quantum-assisted and Quantum-based
Solutions, with Lajos Hanzo, Harald Haas, Dominic O’Brien and Markus Rupp, in "Prolog to
the Section on Wireless Communications Technology", Proceedings of the IEEE,
Volume: 100, Issue: Special Centennial Issue, ISSN: 0018-9219. (Impact Factor:
5.151, IEEE Highest), 2012.
Sandor
Imre, Laszlo Gyongyosi: Quantum-assisted and Quantum-based Solutions in Wireless
Systems, with Lajos Hanzo, Harald Haas, Dominic O’Brien and Markus Rupp, in: "Wireless
Myths, Realities and Futures: From 3G/4G to Optical and Quantum Wireless",
Proceedings of the IEEE, Volume: 100, Issue: Special Centennial Issue, ISSN:
0018-9219. (Impact Factor: 5.151, IEEE Highest), 2012.
Könyv
Sandor Imre and
Laszlo Gyongyosi:
Advanced
Quantum Communications - An Engineering Approach
Publisher:
Wiley-IEEE
Press (New Jersey,
USA), John Wiley & Sons, Inc., The Institute of
Electrical and Electronics Engineers.
Book
Details: Hardcover: 524
pages, ISBN-10: 1118002369, ISBN-13: 978-11180023, Sept.
2012.
Oktatás:
·
Kvantum
infokommunikáció és alkalmazásai (BME-VIHIAV13), Híradástechnikai Tanszék, BME,
www.mcl.hu/quantum
·
Kvantum-informatika
és kommunikáció (BME-VIHIAV06), Híradástechnikai Tanszék, BME,
www.mcl.hu/quantum
arXiv
ArXiv
publikációs lista
C.V.
Gyöngyösi
László 2008-ban szerzett kitüntetéses diplomát a BME Villamosmérnöki és
Informatikai Kar műszaki informatika szakán. Jelenleg doktorjelölt a BME
Villamosmérnöki és Informatikai Kar Híradástechnikai Tanszékén. Főbb kutatási
területei a kvantuminformatika, kvantum-kommunikációs protokollok, valamint a
kvantumkriptográfia.


