 |
BMe Research Grant |

|
BME Doctoral School of Informatics
Department of Telecommunications
Supervisor: Prof. Dr. Imre Sandor
Classical and Quantum Communications with Extremely Noisy Quantum
Channels
I developed a channel coding technique to transmit classical and
quantum information over extremely noisy, initially completely useless quantum
channels. I worked out the mathematical background and proved it's correctness in information
theoretic terms. The method can be used to transmit private information
over insecure channels and for perfect classical or quantum communication with very
noisy quantum channels.
Brief Introduction of Research Place
The Department of Telecommunications of Budapest University of
Technology and Economics in Hungary represents a solid ground of teaching,
researching and developing of Information and Communication Technologies for
more than 60 years. The Department covers primary fields such as Acoustics,
Cryptography, Computing (both classical and quantum), Multimedia, Networking and
Signal processing.
Research Background
In the first decade of the 21st century, many revolutionary
properties of quantum channels were discovered. At the dawn of this millennium
new problems have arisen with many open questions, which have opened the door to
many new promising results such as superactivation of quantum channels. The
superactivation of zero-capacity quantum channels makes possible to use
zero-capacity quantum channels for communication.
Besides the relevance of superactivation, its effectiveness is
strongly limited by the preliminary conditions (such as the channel maps of the
joint structure, or the initial capacities of the channels). Our goal was to
eliminate these drawbacks. We introduced an improved method - called
polaractivation.
The difference of superactivation and our new phenomenon – called
polaractivation –
is summarized in Fig. 1. The set of polaractive quantum channels
involves the set of superactive channels. Our polaractivation provides a more general framework without any preliminary
conditions on the channels or on the initial capacities of the quantum channels
involved in the joint structure.
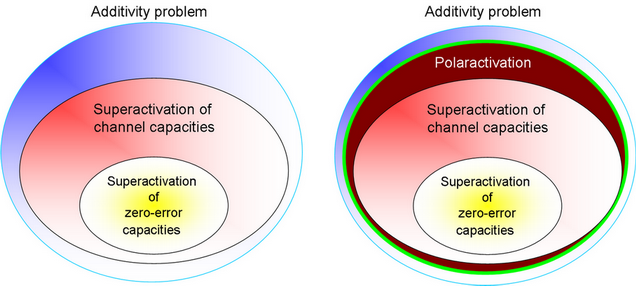
Fig. 1. The problem of superactivation and polaractivation of zero-error
capacity of quantum channels as a sub domain of larger problem sets.
Superactivation (Fig. 2) is limited by several preliminary conditions
on the properties of the quantum channels and on the maps of the channels
involved in the joint channel structure.

Fig. 2. The quantum channels have zero capacities individually, but jointly
they define a structure which can be used to transmit information. [G. Smith, J. Yard, Quantum
Communication with Zero-capacity Channels. Science 321, 1812-1815 (2008)]
Our Solution
I introduced a new phenomenon called polaractivation. Polaractivation
is based on quantum polar encoding and the results are equal to the
superactivation effect – positive capacity can be achieved with zero-capacity
quantum channels. However, polaractivation has many advantages over the
superactivation: it is limited neither by any preliminary conditions on the
quantum channel nor on the maps of other channels involved in the joint channel
structure. We also prove that the polaractivation works for arbitrary quantum
channels. We also derived a lower bound on the symmetric classical capacity,
which is required for the polaractivation of private classical
capacity. Furthermore, we demonstrated that it works for the zero-error
classical and quantum communication.
Polaractivation is based on quantum polar coding and the result is similar to the
superactivation effect – positive capacity can be achieved with zero-capacity
quantum channels. It requires only the multiple uses of the same quantum channel
and our special channel coding scheme.
Fig. 3. Polaractivation has many advantages over superactivation: it is
limited neither by any preliminary conditions on the quantum channel nor on the
maps of other channels involved in the joint channel structure. Furthermore, it requires only the multiple
uses of the same quantum channel.
Polaractivation of Zero-Capacity Quantum
Channels
Polar codes belong to the group of error-correcting codes. They introduce no redundancy, only
operate on codewords of n qubit of
length. They can be used to achieve the symmetric capacity of classical discrete
memoryless channels (DMCs).
The basic idea behind the construction of polar codes is channel selection
called polarization: assuming n
identical DMCs we can create two sets by means of an
encoder. “Good” channels are nearly noiseless while “bad” channels have nearly
zero capacity (Fig. 4). Furthermore, for large enough n, the fraction of good channels
approaches the symmetric capacity of the original DMC.
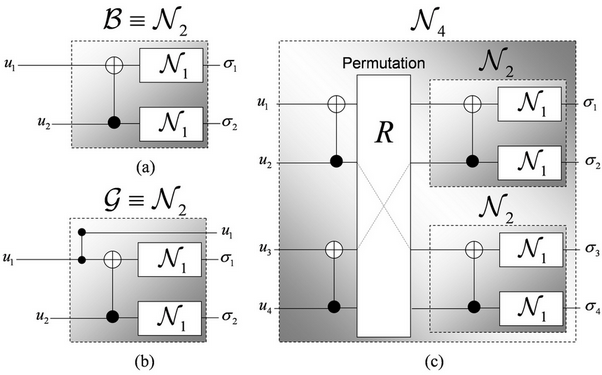
Fig. 4. (a): The ‘bad’ channel: input is not known by Bob. (b): The ‘good’
channel: input is also known on Bob’s side. (c): The recursive channel
construction from two lower-level channels. R is the permutation
operator.
The polaractivation of any symmetric channel capacities of arbitrary
quantum channels requires only the proposed polar encoding scheme and the
multiple uses of the same quantum channel. The positive private capacity will be
obtained after the multiple uses of the quantum channel. An important difference
between superactivation and our polaractivation scheme: while the
superactivation of private classical capacity is not possible, the polaractivation is possible (Fig. 5).
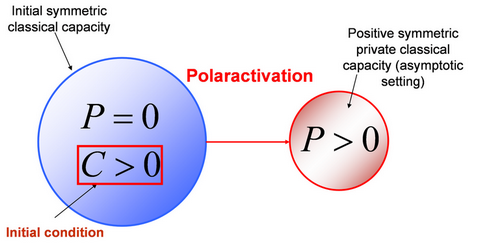
Fig. 5. While the superactivation of private classical capacity is not
possible, the polaractivation is possible.
Results on the polaractivation of quantum channels
As summarized in Fig. 6, the polaractivation will result in the
non-empty set of input polar codewords, and the channel will be able to transmit
classical information privately.
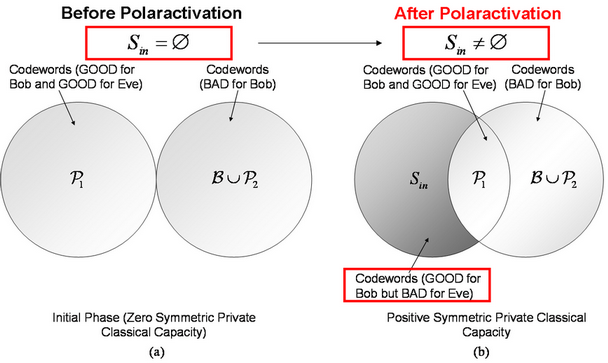
Fig. 6. (a): The brief summarization of the
proposed polaractivation scheme. In the initial phase, input channels cannot
transmit classical information privately. (b): The polaractivation of symmetric
private classical capacity makes it possible to construct codewords capable of
transmitting private classical information between Alice and
Bob.
The polaractivation of symmetric private classical capacity depends
on the amount of available symmetric classical capacity, which can be achieved
by the proposed polar coding technique. The Bhattacharya parameters represent
the noise of the channel: 0 for an idealistic channel, 1 for a completely noisy
channel.
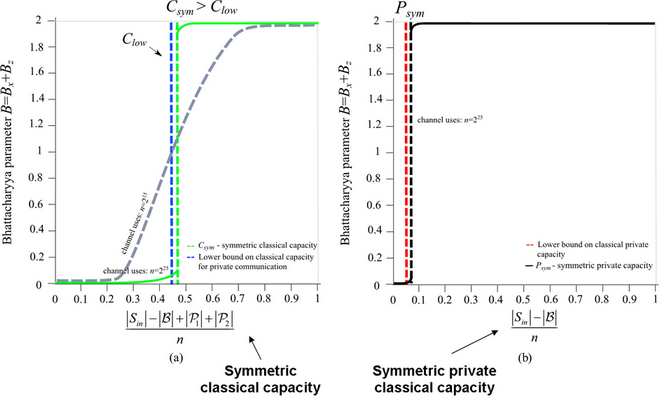
Fig. 7 (a): The ratio of the Bhattacharya parameters of “good” and “bad” channels as the function of the achievable symmetric classical capacity expressed by the codewords of Alice and Bob. As the set converges to the critical lower bound, the symmetric private classical capacity will becomes positive, otherwise positive private capacity is not possible. (b): The ratio of the Bhattacharya parameters of “good” and “bad” channels as the function of the achievable symmetric private classical capacity expressed by the private codewords of Alice and Bob. For high enough number n of channel uses, the critical lower bound on the private classical capacity can be exceeded, as depicted by the black dashed line.
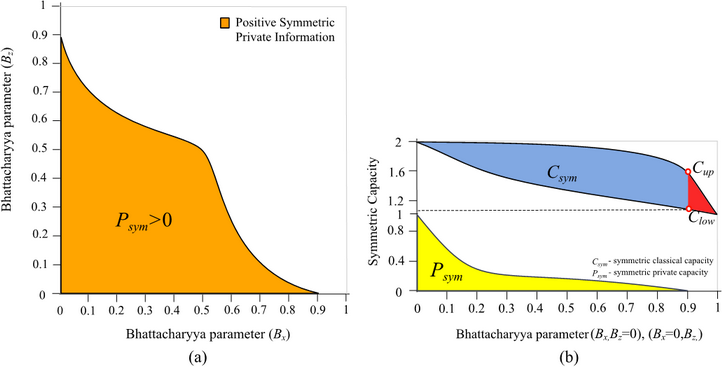
Fig. 8. (a): The Bhattacharya parameters of the
individual amplitude and phase-errors. The private classical capacity will be
greater than zero only in this domain. (b): The achievable symmetric classical
capacity and symmetric private classical capacity as the function of
Bhattacharya parameters. Individually, the channels are so noisy that they are
in the red area; thus they cannot transmit any private classical information.
With the help of quantum polar coding, the initial error probabilities are
re-transformed, and the symmetric classical capacity will be above the critical
lower bound, which makes possible to transmit private classical
information.
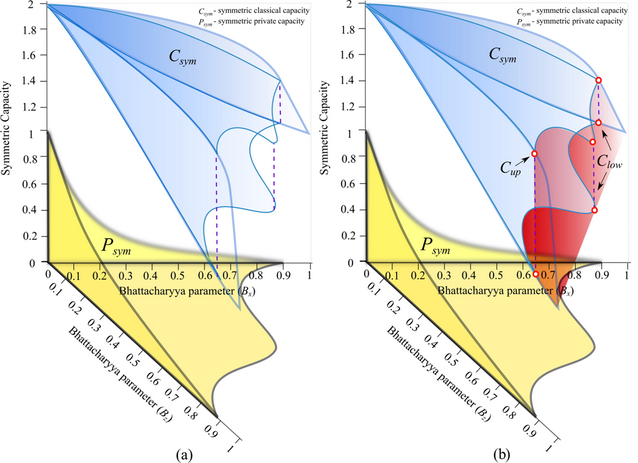
Fig. 9. (a): The achievable symmetric classical capacity (blue) and symmetric private classical capacity (yellow) as the functions of the Bhattacharya parameters of the amplitude and phase transmissions of the noisy quantum channel. (b): The private communication is possible if and only if the polar codes can ensure the symmetric classical capacity above the critical lower bound. In the red area, the channels are so noisy that private communication is not possible. Initially, the input channels are in this area, however, with the help of polar coding, error-probabilities are re-transformed, and the critical lower bound on the symmetric classical capacity can be exceeded, which makes private communication possible.
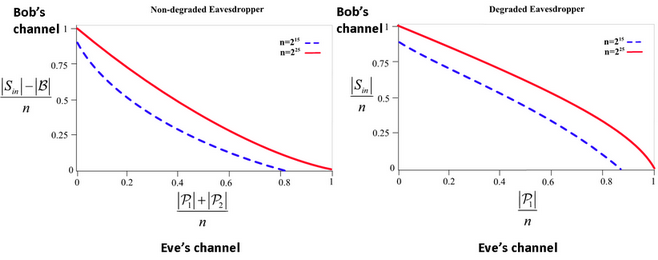
Fig. 10. The achievable private classical communication rate expressed as
Bob’s valuable codewords in the function of Eve’s valuable codewords for a
non-degraded eavesdropper (a) and for a degraded eavesdropper
(b).
Efficiency of polaractivation
Polaractivation is very efficient. Assuming n uses of the noisy quantum channel, the
complexity of the proposed scheme is
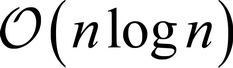
After the channels are being polarized, the
polaractivation of arbitrary quantum channels results in a non-empty set of
polar codewords which set achieves the symmetric capacity of the quantum channel
(Fig. 11).
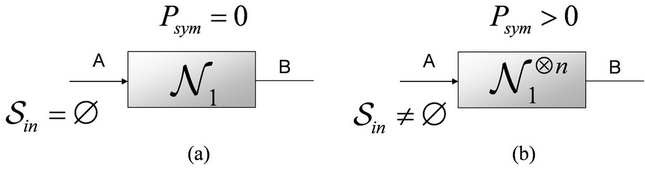
Fig. 11. While the set of polar codewords which can transmit information is
empty in the initial phase (a), by the proposed polaractivator scheme this set can be transformed into a
non-empty set (b).

Fig. 12. The valuable information is being transmitted by a quantum polar
codeword over the polarized channel structure.
Quasi-superactivation of classical capacity of zero-capacity quantum
channels
One of the most surprising recent results in quantum Shannon theory
is the superactivation of the quantum capacity of a quantum channel. This
phenomenon has its roots in the extreme violation of additivity of channel
capacity and enables to reliably transmit quantum information over zero-capacity
quantum channels. In this work, we demonstrate a similar effect for the classical
capacity of a quantum channel which previously was thought to be impossible. We
show that a nonzero classical capacity can be achieved for all zero-capacity
quantum channels and it only requires the assistance of an elementary
photon-atom interaction process – the stimulated emission.
Importance of our discovery
Sending classical information over a channel combination in which
each channel has zero classical capacity seemed to be impossible. The transmission of classical information over
zero-capacity quantum channels seemed to be the biggest problem of all, and
it also had its roots in Hastings’ counterexample. As was found in 2009, the Holevo
information is non-additive in general; on the other hand, this result did not
give an answer to the general case of the classical capacity, and also left open
many new questions. It was found that in some very special cases quantum
information can be transmitted in a similar scenario, however, the most general
issue – the transmission of classical information over such a structure – could not be solved.
The phenomenon we propose in this work is called quasi-superactivation. The result is
similar to the superactivation effect – positive capacity can be achieved with
noisy quantum channels that were initially completely useless for communication.
An important difference is that quasi-superactivation is limited neither by any
preliminary conditions on the initial private capacity of the channel nor on the
maps of other channels involved in the joint channel structure.
Quasi-superactivation only requires the addition of quantum entanglement and the use of stimulated emission; then arbitrary zero-capacity quantum channels can be used for classical communication (Fig. 13). We show that classical information can also be transmitted over the combination of zero-capacity quantum channels using quasi-superactivation and it only requires the most natural process that occurs during stimulated emission. Another important difference is that contrary to the superactivation of classical capacity of quantum channels – which is theoretically impossible, here we prove that – quasi-superactivation is possible.
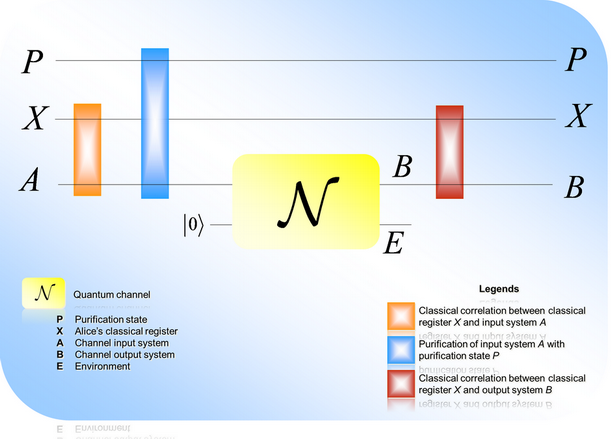
Fig. 13. Alice’s classical register is denoted by
X, the input system is A while P is the purification state. The
environment of the channel is denoted by E, the output of the channel is B. The quantum channel has positive
classical capacity if and only if the channel output system B will be correlated with Alice’s
classical register X.
In Fig. 14, we show our channel construction. The first channel can
be any zero-capacity quantum channel that produces a maximum possible mixed output
state (The channel output is completely uncorrelated with the input, i.e., the
classical capacity of the channel is zero, since the channel destroys every
classical correlation.). The second channel in the channel construction is the
so-called cloning quantum channel,
which channel model describes a natural process that occurs during stimulated emission.
The cloning channel describes the effect of optical amplification as
a result of the fundamental interaction of an atom with an impinging photon. The
effect is known as stimulated emission and occurs, for instance, in erbium-doped
optical fibers. Furthermore, it was also found that the qudit Unruh channel has deep connection with the cloning
channels.
As follows, the stimulated emission has deep relevance in the
quasi-superactivation of the classical capacity of quantum channels. The process
that occurs during the stimulated emission is described and modeled by the
cloning quantum channel.
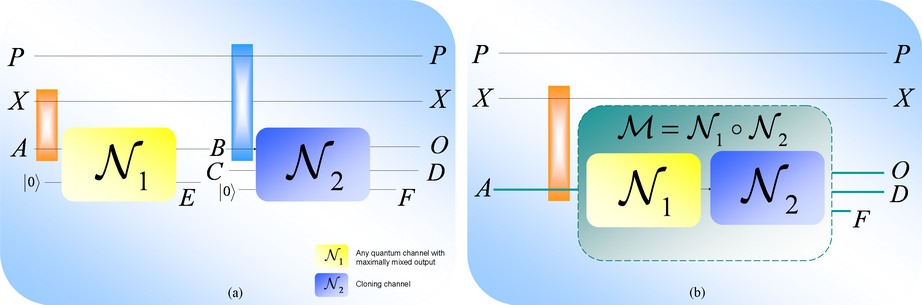
Fig. 14. (a): The first quantum channel can be any quantum channel that
produces a maximally mixed output state. The second channel is the cloning
channel. Alice’s classical register is denoted by X, the channel input is A, while P is the purification state (it describes the connection
with the environment). In the sending process Alice correlates her quantum
system A with her classical register X (orange-shaded rectangle). The first channel destroys every classical
correlation between register X and channel output B. The input of
the second channel is the output B of
the first channel. The purification of system B is denoted by the
blue-shaded rectangle. The environment of the first channel is depicted by E. The output of the channel is
O, while D is the cloned output and F is the environment. (The environments
of the channels are initialized in the pure input
system.)
As we have found, while individually quantum channel M cannot used to transmit any classical
information (Fig. 15(a)), but something strange occurs if we use
two of these zero-capacity channels jointly where each channel is
constructed from a zero-capacity quantum channel and a cloning quantum channel
(Fig. 15(b)).
As we have found, two zero-capacity quantum channels in a joint
structure can activate each other, and the joint classical capacity will be
positive, while the individual classical capacities are zero.
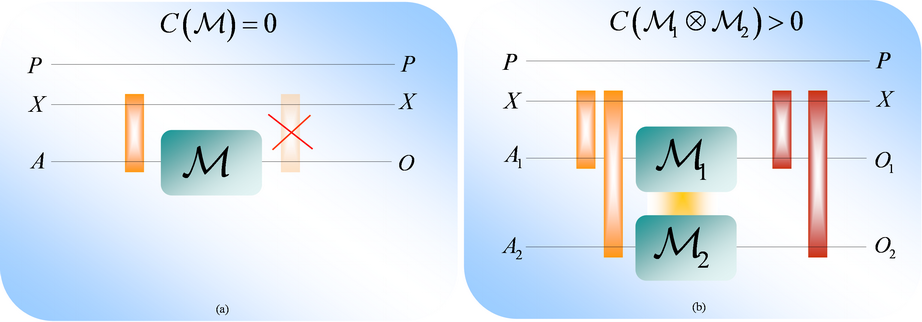
Fig. 15. (a): Individually quantum channel M cannot transmit any classical
information. The channel destroys every classical correlation between Alice’s
classical register X and channel output O.
(b): For the combination of the two zero-capacity quantum channels with zero classical capacities, the joint classical capacity will be positive. Any correlation between classical register X and output systems will occur that result in positive classical capacity.
Fig. 16 helps explain what is happening in the background and how the
quasi-superactivation of classical capacity works.
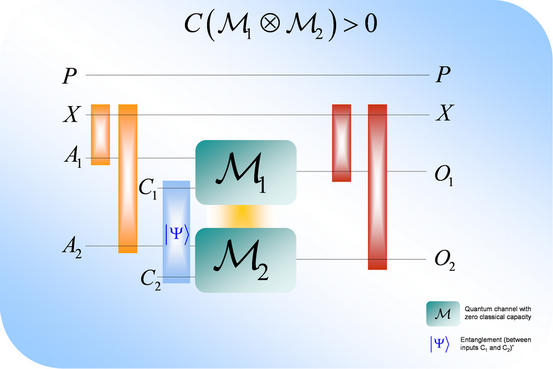
Fig. 16. The detailed view of joint channel construction helps reveal the
effect. Individually, neither M1, nor M2 can transmit any classical
information. On the other hand, if we use entangled auxiliary input and the amount of
entanglement in the input qubits is chosen from a very limited domain, then the two
channels can activate each other and classical information can be transmitted.
Using input states with this special amount of entanglement, the outputs of the
joint channel construction will be correlated with each other and some
correlation will also occur with the classical register X. However,
individually every classical correlation will vanish,
jointly some correlation can be produced at the channel output which leads to
positive classical capacity.
The requirements
for the amount of entanglement in the input system for the quasi-superactivation
are also summarized in Fig. 17.
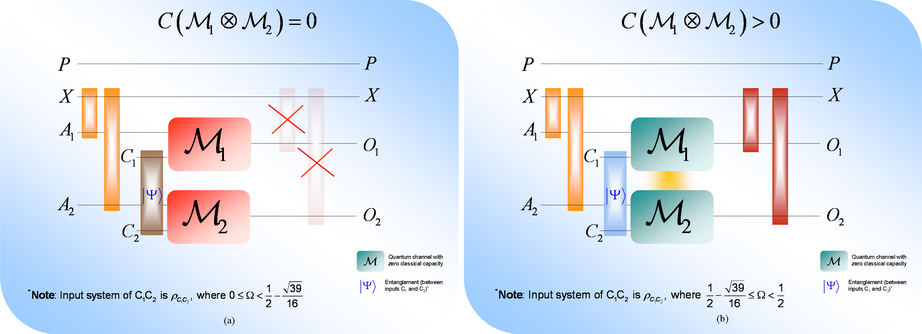
Fig. 17. (a): If the amount of
entanglement in the auxiliary input system of the joint channel is chosen
inappropriately, then the channel construction cannot be used to transmit any
classical information, and the quasi-superactivation effect will not occur. In
this case, any classical correlation between register X and channel outputs will completely
vanish.
(b): The classical capacity of the joint channel structure will be positive if and only if the amount of entanglement in the auxiliary input system is chosen from a very tight domain by Alice. In this case, classical correlation between register X and outputs will occur on the channel output.
As we have found, the level of quasi-superactivation depends on the
amount of entanglement in the inputs of the joint structure and the classical
capacity can be greater than zero only in a well-specified strict domain (Fig.
18).
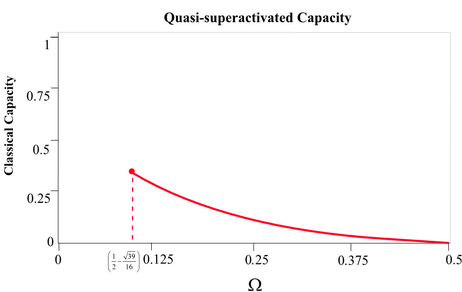
Fig. 18. The level of quasi-superactivated classical capacity of the joint
structure depends on the amount of entanglement in the EPR input that was fed by
Alice to the inputs of the joint channel structure.
Pilot Quantum-Error Correction
In space-earth quantum communications, the relative motion of the
ground station and the satellite causes a rotation in the polarization of the
quantum states. Current approaches to the compensation for these types of
polarization errors require high computational costs and extra physical apparatuses. Our newly developed lightweight quantum error-correction scheme fixes
the polarization errors without redundant encoding, which is critical in
space-earth quantum communication systems. The proposed solution can be
implemented in practice without any extra hardware or software costs, providing
an easily implemented on-the-fly polarization compensation scheme for future
space-earth quantum communications.
The proposed error correction scheme is based on the usage of pilot
states. The pilot states are ordinary known quantum states, sent by Alice to the
quantum channel. However, Alice does not place any data in these states - these
states will merely be used for error correction. The pilot states will store the
unknown map of the quantum channel. These pilot states – using a simple Hadamard
and Controlled-NOT (CNOT) gates – can be used to correct an arbitrarily high
number of data quantum states sent through the quantum channel. However, all of
these states are unknown, Bob is able to construct these states using our simple
quantum circuit. The angle of the polarization rotation is stored in the pilot
quantum state without making process tomography on the channel. The simplicity
of the proposed error-correction quantum circuits allows easy
implementation in practice.
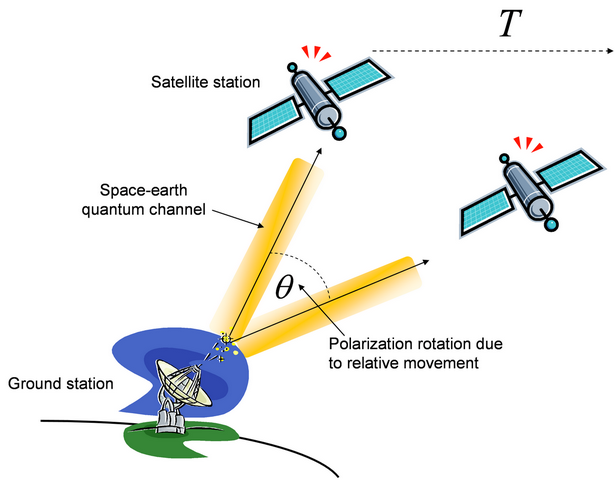

Fig. 19. (a): The relative motion of the ground and satellite stations causes
a rotation in the polarization of the qubits. (b): The correction of an
arbitrary unknown state (d) can be
achieved by the unknown pilot states (theta) and elementary quantum
gates (CNOT, Hadamard).
My proposed pilot channel coding scheme was presented at the First
NASA Quantum Future Technologies Conference (NASA Ames Research Center, Moffett
Field, California, USA.), and at the Second International Conference on Quantum
Error Correction (QEC11), Dec. 2011, University of Southern California, Los
Angeles, USA).
Research Summary
In this work, I introduced the term polaractivation. The result of
polaractivation is similar to the superactivation effect, but without the necessary
preconditions on the quantum channels or on the joint structure. The
polar coding is a revolutionary channel coding technique, which makes it
possible to achieve the symmetric capacity of a noisy communication channel by
the restructuring of the initial error probabilities. In the case of a quantum
system, the problem is more complicated, since the error characteristic of a
quantum communication channel significantly differs from the characteristic of
quantum communication channels.
I introduced the term quasi-superactivation. We proved that by
adding quantum entanglement to zero-capacity quantum channels, classical
information transmission is possible. The quasi-superactivation is similar to
the superactivation effect, thus positive capacity can be achieved with noisy
quantum channels that were initially completely useless for classical
communication. However, an important difference is that quasi-superactivation is
limited neither by any preliminary conditions of the originally introduced
superactivation effect nor on the maps of other channels involved in the joint
channel structure. As we have proved, additionally to the existence of zero-capacity
quantum channels with positive quantum capacity, finding
zero-capacity quantum channels with individually zero classical capacities,
which if employed in a joint channel construction can transmit classical
information is also possible.
We hope that our results help reveal the strange and mysterious world
of quantum information, and also characterize and exploit the hidden possibilities
in information transmission over quantum channels in future communication systems
and networks. The proposed scheme uses only very simple elements,
which allows for a very effective implementation and verification in
practice.
Acknowledgments
The results discussed above are supported by the grant
TAMOP-4.2.1/B-09/1/KMR-2010-0002, 4.2.2.B-10/1--2010-0009 and COST Action
MP1006.
References
E.
Arikan. Channel polarization: A method for constructing capacity achieving codes
for symmetric binary-input memoryless channels. IEEE Transactions on Information
Theory, 55(7):3051–3073, July 2009.
arXiv:0807.3917.
H.
Mahdavifar and A. Vardy. Achieving the Secrecy Capacity
of Wiretap Channels Using Polar Codes. arXiv:1001.0210v2 [cs.IT], April 2010.
M.
M. Wilde and S. Guha. Polar codes for classical-quantum channels.
arXiv:1109.2591v1 [quant-ph], September 2011.
K. Bradler, An infinite
sequence of additive channels: the classical capacity of cloning channels. IEEE
Trans. Info. Theory, vol. 57, no. 8, arXiv:0903.1638,
(2011)
K.
Bradler, P. Hayden, D. Touchette, and
M. M. Wilde, Trade-off capacities of the
quantum Hadamard channels, Journal of Mathematical Physics 51, 072201,
arXiv:1001.1732v2, (2010).
A.
Holevo, “The capacity of the quantum channel with general signal states”, IEEE
Trans. Info. Theory 44, 269 - 273 (1998).
B.
Schumacher and M. Westmoreland, “Sending classical information via noisy quantum
channels,” Phys. Rev. A, vol. 56, no. 1, pp. 131–138,
(1997).
S.
Lloyd, “Capacity of the noisy quantum channel,” Phys. Rev. A, vol. 55, pp.
1613–1622, (1997)
P.
Shor, “The quantum channel capacity and coherent information.” lecture notes,
MSRI Workshop on Quantum Computation, Available online at
http://www.msri.org/publications/ln/msri/2002/quantumcrypto/shor/1/.
(2002).
I.
Devetak, “The private classical capacity and quantum capacity of a quantum
channel,” IEEE Trans. Inf. Theory, vol. 51, pp. 44–55, quant-ph/0304127,
(2005).
G.
Smith, J. Yard, Quantum Communication with Zero-capacity Channels. Science 321,
1812-1815 (2008)
G.
Smith, J. A. Smolin and J. Yard, Gaussian bosonic synergy: quantum communication
via realistic channels of zero quantum capacity, arXiv:1102.4580v1, (2011).
R. Duan, Superactivation of zero-error capacity of noisy quantum
channels.arXiv:0906.2527, (2009)
T. S. Cubitt, G. Smith,
Super-Duper-Activation of Quantum Zero-Error Capacities, arXiv:0912.2737v1.
(2010).
T.
Cubitt, D. Leung, W. Matthews and A. Winter, Improving
Zero-Error Classical Communication with Entanglement, Phys. Rev. Lett. 104,
230503 (2010), arXiv:0911.5300 [quant-ph]
T. Cubitt, J. X. Chen, and A.
Harrow, Superactivation of the Asymptotic Zero-Error Classical Capacity of a
Quantum Channel, arXiv: 0906.2547. (2009)
F.G.S.L. Brandao, J. Oppenheim and S. Strelchuk, "When does
noise increase the quantum capacity?", arXiv:1107.4385v1 [quant-ph]
(2011)
M.
Christandl, A. Winter, Uncertainty, Monogamy, and
Locking of Quantum Correlations, IEEE Trans Inf Theory, vol 51, no 9, pp 3159-3165 (2005).,
arXiv:quant-ph/0501090.
Results
Conference Publications
The results have been published at conferences on quantum
information:
- Massachusetts
Institute of Technology (MIT), (Cambridge, USA)
- Stanford
University (USA)
- First NASA
Quantum Future Technologies Conference (NASA Ames Research Center, Moffett
Field, California, USA.)
- University of
Tokyo (Tokyo, Japan)
- University of
Southern California (Los Angeles, USA)
- University of
Oxford, (United Kingdom)
- University of
Montreal (Canada)
- University of
Cambridge (Cambridge, UK),
- University of
Harvard (Cambridge, USA),
- University of
Berkeley (California, USA),
- Princeton
University (New Jersey, USA),
- University of
Arizona (Arizona, USA);
- University of
Ottawa (Canada)
- University of
Queensland (Australia),
- University of
Southampton (UK),
- National
Institute of Informatics, Tokyo (Japan),
- Nanyang
Technological University, (Singapore).
Publications
The results on additivity and superactivation analysis of quantum channels have been published in many journals (published by IEEE, Elsevier, Springer, Wiley, etc.)
Proceedings
of the IEEE (Special Centennial Celebration Issue)
Two articles have been published in the Special Centennial Celebration Issue of the Proceedings of the IEEE.
100th Year
Anniversary Celebration Volume of the Proceedings
of the IEEE (Special
Centennial Celebration Issue: Reviewing the Past, the Present, and the
Future of Electrical Engineering Technology and the
Profession)
Sandor
Imre, Laszlo Gyongyosi: Introduction to Quantum-assisted and Quantum-based
Solutions, with Lajos Hanzo, Harald Haas, Dominic O’Brien and Markus Rupp, in "Prolog to
the Section on Wireless Communications Technology", Proceedings of the IEEE,
Volume: 100, Issue: Special Centennial Issue, ISSN: 0018-9219. (Impact Factor:
5.151, IEEE Highest), 2012.
Sandor
Imre, Laszlo Gyongyosi: Quantum-assisted and Quantum-based Solutions in Wireless
Systems, with Lajos Hanzo, Harald Haas, Dominic O’Brien and Markus Rupp, in: "Wireless
Myths, Realities and Futures: From 3G/4G to Optical and Quantum Wireless",
Proceedings of the IEEE, Volume: 100, Issue: Special Centennial Issue, ISSN:
0018-9219. (Impact Factor: 5.151, IEEE Highest), 2012.
Book
Sandor Imre and
Laszlo Gyongyosi:
Advanced
Quantum Communications - An Engineering Approach
Publisher:
Wiley-IEEE
Press (New Jersey,
USA), John Wiley & Sons, Inc., The Institute of
Electrical and Electronics Engineers.
Book
Details: Hardcover: 524
pages, ISBN-10: 1118002369, ISBN-13: 978-11180023, Sept.
2012.
Teaching activity and Conference Organizing
Quantum Computing and Communications (BME-VIHIAV06), Department of Telecommunications, BUTE
arXiv
My papers on the
arXiv
Short C.V.
Laszlo Gyongyosi received the M.Sc. degree in Computer Science with
Honors from the Budapest University of Technology and Economics (BUTE) in 2008.
He is a Ph.D. Candidate at the Department of Telecommunications, BUTE. His
research interests are in Quantum Channel Capacities, Quantum Computation and
Communication, Quantum Cryptography and Quantum Information Theory. Currently,
he is completing a book on advanced quantum communications, and he teaches
courses in Quantum Computation. In 2009, he received Future Computing Best Paper
Award on quantum information, in 2010, he was awarded
the Best Paper Prize of University of Harvard, USA. In 2010, he obtained a Ph.D.
Grant Award from University of Arizona, USA. In 2011, he received the PhD
Candidate Scholarship at the Budapest University of Technology and Economics,
the Ph.D. Grant Award of Stanford University, USA, the award of University of
Southern California, USA, and the Ph.D. Grant Award of Quantum Information
Processing 2012 (QIP2012), University of Montreal, Canada. In 2012 he received
the PhD Grant Award of APS DAMOP 2012 from the Division of Atomic, Molecular,
and Optical Physics of the American Physical Society (APS), California, USA,
2012.


