Pal Csonka Doctoral School 

BME Építészmérnöki Kar, Department of Morphology and Geometric Modeling Morphodynamics

Supervisor: Dr. SIPOS András

Fracture pattern of inflated elastic brittle rings

Introducing the research area

Many examples of arches, vaults, or cupolas having undergone partial fracture, yet still standing can be observed around us. In masonry domes, the load-bearing mechanism of the structure transforms its self-weight into tensile hoop stresses. Due to the limited tensile capacity of the material, topology change through fracture is necessary to relax these stresses and reach a static equilibrium configuration. As cracking is an irreversible process, the observable pattern carries information about the history of a structure. Understanding and characterizing the pattern formation is an indispensable step toward analyzing real structures based on their visible cracking pattern.

Brief introduction of the research place

I conduct my research on the premises of the Department of Morphology and Geometric Modeling under the supervision of Dr. András A. Sipos. In addition to research, we teach mathematics and geometry-related classes for architecture students.

History and context of the research

Brittle domes are known to exhibit a typical cracking pattern of almost-equidistant cracks expanding upwards along meridians of the cupola till some height determined by the geometry [3] (Fig. 1). The cracked dome stability problem became famous in the 18th century following the work of G. Poleni on St Peter’s Basilica in Rome [1]. Splitting the fragmented dome into pairs of lunes he assumed to behave like arches, the mathematician leveraged Hooke’s hanging chain theorem to prove that the cracked dome is stable (Fig. 1). If the static stability question is settled, the emergence of the pattern is not. In particular, the order of appearance of the cracks is still unrevealed. Recently, the anchorage of fracture in a variational framework offered new possibilities to describe and analyze the pattern appearance process [5,6].

 

Figure 1. (Left) Geometric characteristics and cracking pattern in the dome of the Pantheon in Rome as per [6]. (Right) Poleni’s sketch with a section of the cupola of St Peter’s and the associated weighted hanging chain in [1]. The reflection of the hanging chain fits in the thickness of the dome, proving the arches' stability as per Hooke’s theorem.

 

In the variational formulation of fracture, the observed macro-phenomenon is described by a competition between a bulk energy containing contributions from the elastic energy and the work of external forces, and a fracture energy associated with the creation of new material surfaces [2,4]. Since the elastic response and the topology of a solid are intimately linked, the problem is in general fully coupled. In addition, the appearance of new cracks needs to be consistent with the empirical observations of the strength of materials [9]. Overall, the determination of the nucleation of new cracks from a defect-free part of a solid is particularly delicate [7], as the pattern stems from the requirement of energy minimization under the constraint that material strength is reached.

The research goals, open questions

The primary aim of my research is the accurate prediction of the cracking pattern of a brittle hemispheric dome, and the identification of its main drivers in the context of a quasi-static load increase. To this end, I seek answers to the following questions:

1. What are the main geometrical and material parameters characterizing the observed pattern?
2. What is the interplay between topological changes of the structure due to cracking and elastic response in its pristine part?
3. How do existing cracks affect further crack formation?
4. How do the dome support features affect the pattern?
5. Can the fracturing dome be accurately represented by a dimension-reduced model, while retaining the pattern features?

Methods

Dimension reduction

Both experiments and finite element simulations show that cracks in a brittle dome appear almost instantaneously, along meridians, and up to a precise height. Noticing that cracks nucleate and expand from the bottom part of the dome, and exploiting axisymmetry, we model the cracking initiation in an equivalent planar ring. This ring is not a constraining ring, nor is it a part of the dome, but a model associated with the lower part of the dome. It consists of a collection of fragments whose extremities’ positions are given by cracks. The problem of the evolution of the ring cracking pattern is formulated in a variational framework.

 

    

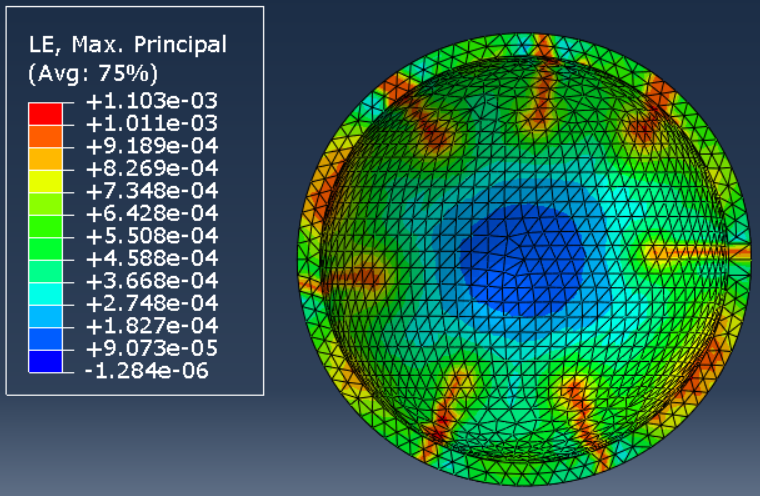
Figure 2. (Left) Principal strain in a dome simulated with finite elements. The red bands are cracks. (Right) Model of the 3D structure with 7 cracks in red. Cracks nucleate from the blue zone. We study a mechanical model of a fictitious ring associated with this area.

 

Mechanical behavior modeling and analytical treatment

In the first step, a ring allowed to expand only radially is considered (Fig. 3). Its elastic energy includes contributions from both bending and stretching. A quasi-statically increasing, outward-pointing inflating pressure mimics the bulging-out of the dome bottom part caused by its load-bearing mechanism, and the radial displacement is obstacled by spring accounting for the constraining effects of both the dome cap and its supports. As hoop-stress relapse from fracture is impossible, an additional relaxation parameter penalizes the elastic part of the energy on fragment breaking. Assuming non-interacting crack faces, a sequence of systems of boundary value problems is solved. The pattern formation can be studied from the comparison of the variation of the global energy against test cracks in individual fragments.

           

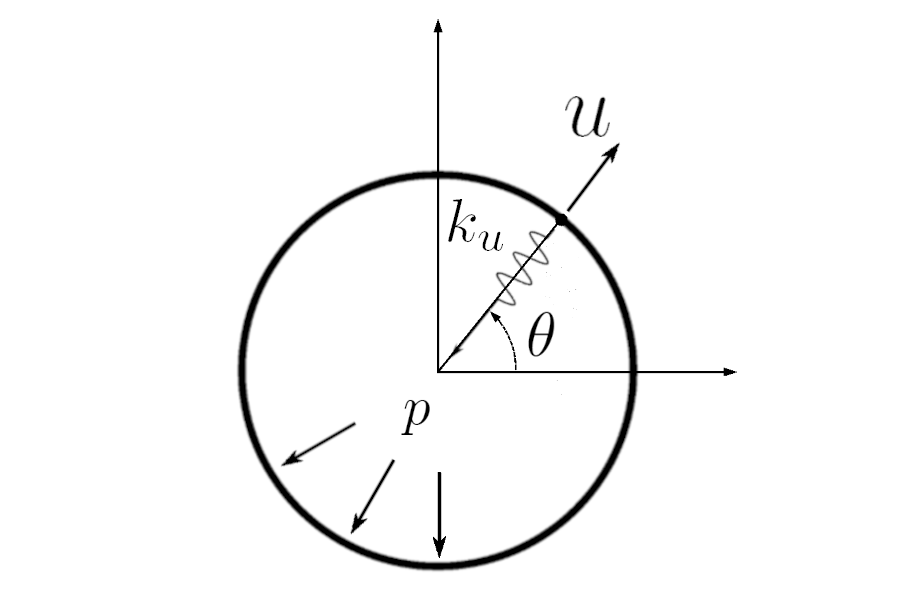
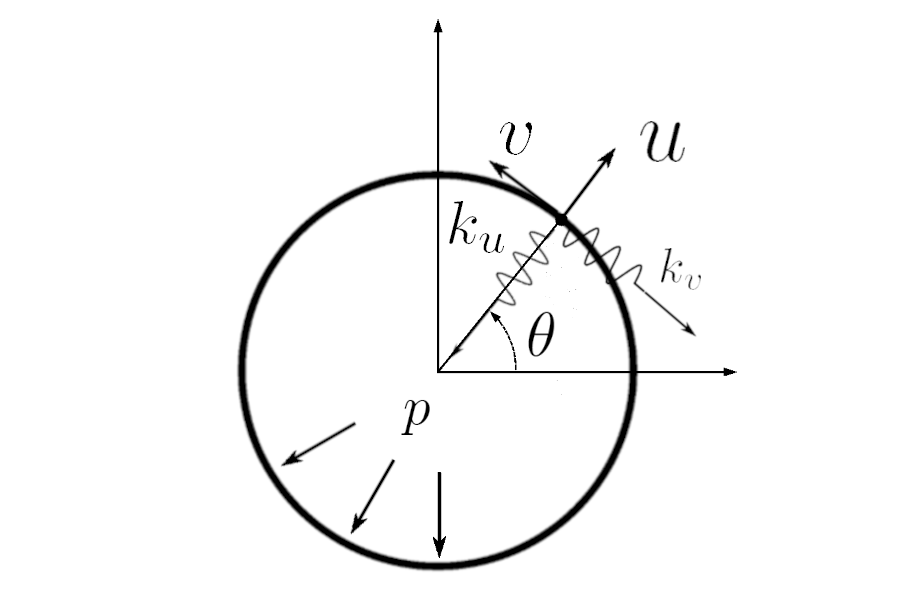
Figure 3. Mechanical models of the planar ring associated with the dome. (Left) Model 1 allows only radial displacement (u). (Right) Model 2 allows tangential displacement (v). Associated constraining springs (k_u, k_v) and internal pressure (p) are shown.

 

Numerical simulations

The model is extended to include radial and tangential displacements (Fig. 3), making it more physical but requiring numerical treatment. An analysis of the sensitivity of the produced pattern to the various parameters of the model is performed. In addition, the effect of support stiffness features on the pattern formation process is investigated.

 

Parameters estimation

Finally, as we did not rigorously derive our dimension-reduced model from a 3D continuum formulation, we propose to match the models. We naturally assign the dome cracking pattern to that of a ring by looking only at the pattern trace on the dome mid-surface equator. Parameter fitting, in turn, can be reduced to the minimization of the Hausdorff distance between two collections of singleton.

Results

    Bending is a key driver of pattern formation

By examining the cracking of a single fragment with model 1, we find that its own length is a critical parameter determining the position of the occurrence of further cracks from energy minimization. For small fragments, only the midpoint is an allowed crack position, while for longer fragments, two symmetrical cracking positions coexist (Fig. 4). In the relative cracking position-fragment length phase plane, the energy minima are analytically proven to undergo a supercritical pitchfork bifurcation that vanishes if bending is not considered. The critical fragment length at which the bifurcation occurs depends on the material parameters. This underlines the key role of the bending in driving pattern formation in the fragment.

 

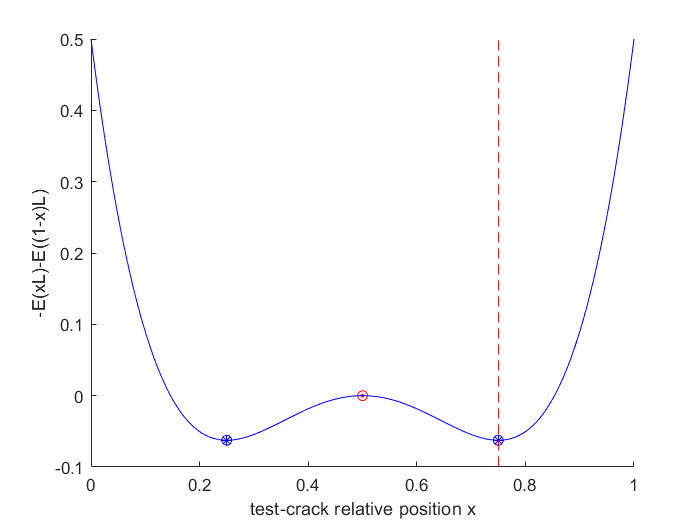
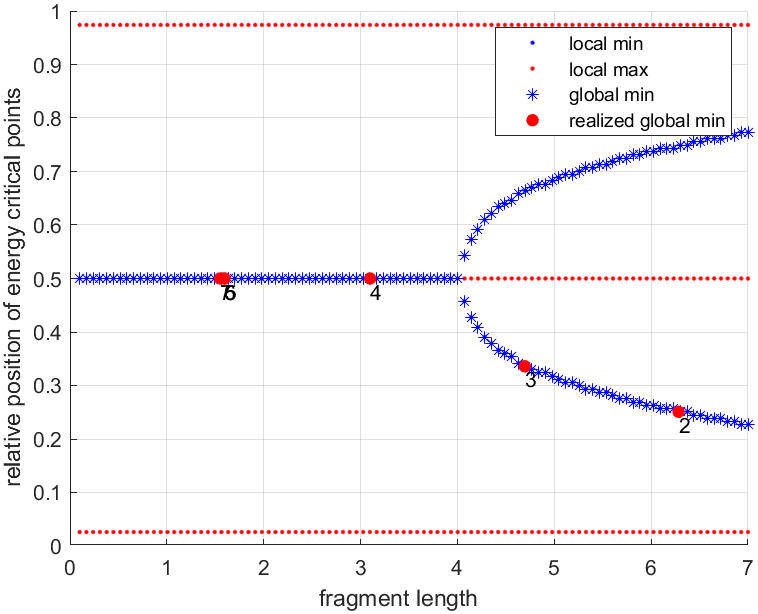
Figure 4. (Left) Dimensionless energy change against relative fragmentation position at a given fragment length. (Right) Phase plane representation of the energy landscape with visible bifurcation. Realized, discrete events are red dots. In both pictures, the global minima are shown with blue asterisks.

 

Topology evolution drives elastic response bifurcations

The pattern formation is driven by the collective behavior of a finite number of fragments, whose individual lengths vary in a discrete manner – as only a fragment of positive length can be created from fracture. The realizations of cracking events in the phase plane are discrete events, and the process proceeds in jumps. As fragmentation continues, the size of the largest fragment ultimately decreases, and the bifurcation length is exceeded. The minimum position jumps from the nontrivial branches of the bifurcation diagram back to the trivial branch. At the observable level, the pattern formation changes. When the global minimum belongs to the nontrivial branches, almost equally spaced cracks are produced, whereas cracks halve existing fragments when the minimum is on the trivial branch (Fig. 5).

 

Parameters governing the crack spacing

In the case of model 2, we first investigate the case of a rotation-invariant functional (e.g., the pressure, spring stiffnesses, and material parameters are constant). The numerical sensitivity analysis reveals that a rich bifurcation landscape drives the pattern formation. The key parameters deciding the position of the new cracks are the ratio of the radial to tangential springs and the length of the fragment undergoing fracture. Regardless, the pattern evolution at the observable level consists of alternates between two regimes, producing either regularly disposed cracks or halving the existing fragments.

 

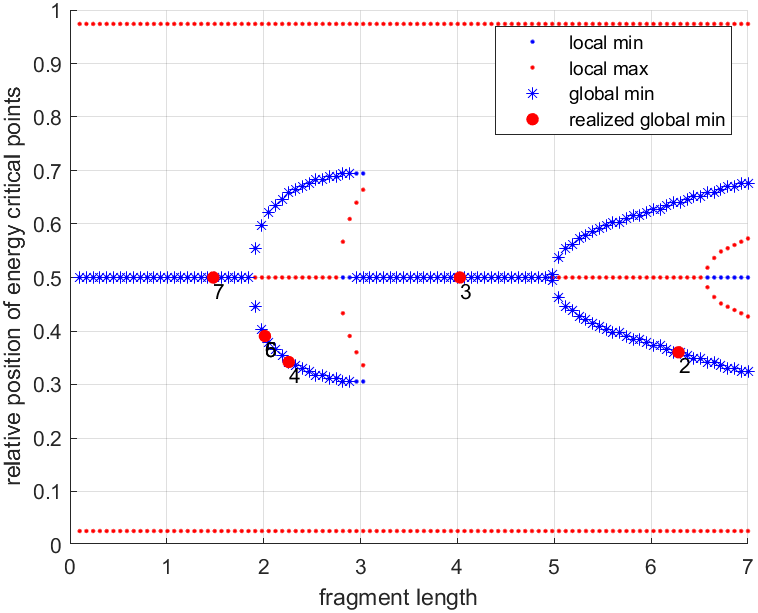
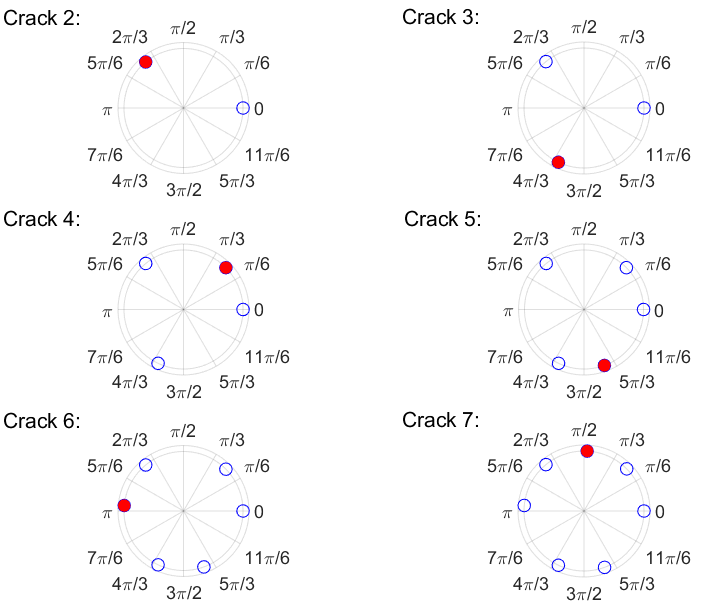
Figure 5. Evolution of the pattern in the phase plane and observed pattern with model 2. Realized events are labeled in the phase plane by their crack number. The discrete evolution jumps over the bifurcation points. Note that cracking events 4, 5, and 6 belong to the same nontrivial branch and produce similar fragments.

 

The pattern is robust against small-amplitude support perturbation

Finally, we show numerically the robustness of the pattern against spring stiffness variations. Low amplitude perturbations of the support stiffness do not fundamentally alter the resulting pattern, whereas strong perturbations trigger the formation of cracks in clusters around points of maximal stiffness.

Expected impact and further research

Our results complement the existing literature on the static equilibrium of masonry domes and provide a way to predict and control the produced pattern [P2]. Analyzing the differences between the computed and actual patterns offers new possibilities for analyzing existing structures [P1]. In addition, the insights gained about the interaction between elastic response and formed pattern is a valuable addition [P3]. Further research is expected to transfer the results to a two-dimensional plane setup, where the control of the formed pattern finds industrial applications.

 

Publications, references, links

List of corresponding own publications.

 

[P1] Michel, S., Sipos, A. A. (2022). On the cracking patterns of brittle rings with elastic radial support under hydrostatic pressure. Meccanica, 57(7), 1639–1656.

 

[P2] Michel, S., Sipos, A.A. (2022). A numerical study of the cracking pattern of reinforced concrete rings under hydrostatic pressure, Proceedings of the 14th fib International PhD Symposium in Civil Engineering, 361–367.

 

[P3] Michel, S., Sipos, A. A. (2023). Fragmentation of inflated elastic brittle rings: Emergence of the quasi-equidistant spacing of cracks. Journal of the Mechanics and Physics of Solids, 179, 105372.

 

[P4] Michel, S. (2024) Part-through cracks computation in an Euler–Bernoulli beam model. Acta Mech, 235, 1165–1174.

 

Table of links.

 

MTMT profile

Dept. Morphology and Geometric Modeling

Pictures of domes

 

List of references.

 

[1] Poleni, G., Poleni, J. (1748). Memorie Istoriche Della Gran Cvpola Del Tempio Vaticano, E De'Danni Di Essa, E De'Ristoramenti Loro, Divise in Libri Cinqve. Nella Stamperia del seminario.

 

[2] Griffith, A. A. (1921). VI. The phenomena of rupture and flow in solids. Philosophical Transactions of the Royal Society of London. Series A, containing papers of a mathematical or physical character, 221(582-593), 163–198.

 

[3] Heyman, J., Poleni, G. (1988). Poleni's problem. Proceedings of the Institution of Civil Engineers, 84(4), 737–759.

 

[4] Bourdin, B., Francfort, G. A., Marigo, J. J. (2008). The variational approach to fracture.

Journal of Elasticity, 91, 5–148.

 

[5] Lancioni, G., Royer-Carfagni, G. (2009). The variational approach to fracture mechanics. A practical application to the French Panthéon in Paris. Journal of Elasticity, 95, 1–30.

 

[6] Masi, F., Stefanou, I., Vannucci, P. (2018). On the origin of the cracks in the dome of the Pantheon in Rome. Engineering Failure Analysis, 92, 587–596.

 

[7] Tanné, E., Li, T., Bourdin, B., Marigo, J. J., & Maurini, C. (2018). Crack nucleation in variational phase-field models of brittle fracture. Journal of the Mechanics and Physics of Solids, 110, 80–99.

 

[8] Grillanda, N., Chiozzi, A., Milani, G., & Tralli, A. (2019). Collapse behavior of masonry domes under seismic loads: an adaptive NURBS kinematic limit analysis approach. Engineering Structures, 200, 109517.

 

[9] Kumar, A., Bourdin, B., Francfort, G. A., & Lopez-Pamies, O. (2020). Revisiting nucleation in the phase-field approach to brittle fracture. Journal of the Mechanics and Physics of Solids, 142, 104027.

 

 

 

.