|
|
BMe Research Grant |
|
George A. Olah Doctoral School of Chemistry and Chemical Technology
BME VBK, Department of Physical Chemistry and Materials Science, Laboratory of Plastics and Rubber Technology
Supervisor: Dr. KÁLLAY-MENYHÁRD Alfréd
Prediction of tensile modulus of semicrystalline polymers based on a single calorimetric curve
Introducing the research area
The optimization of mechanical properties of semicrystalline polymeric materials has been of crucial importance in the past decades since the targeted modifications of the crystalline structure are accompanied by proportional changes in properties [1]. Several micromechanical models have been developed to demonstrate and predict the mechanical behavior of semicrystalline polymers [2-5]. Most of the models require complex and time-consuming calculations and constants which are not known for most of the polymers. Another main disadvantage of some of these approaches is that they are not valid in the entire crystallinity range. In my research, I employ a recently developed simple empirical model which tackles these aforementioned issues. The required parameters for the model equation can be easily obtained from a single melting curve [6]. The primary focus of my current study is to apply this model to a wider range of polymers and predict their mechanical behavior accurately.
Brief introduction of the research place
I have been conducting my doctoral research under the supervision of Dr. Alfréd Kállay-Menyhárd at the Department of Physical Chemistry and Materials Science, specifically at the Laboratory of Plastics and Rubber Technology. Our Laboratory has long-term experience in the materials science field and all the necessary equipment is available for the research. The main focus of my research is to investigate structure-property correlations in semicrystalline polymers with the guidance of my supervisor Dr. Menyhárd who actively contributes to this field.
History and context of the research
In a pioneering study, an empirical model equation was reported by Pukánszky et al. that links the stiffness of polypropylene with crystallization characteristics: enthalpy and peak temperature of crystallization [7]. The major advantage of this simple empirical approach was that it considered crystallinity proportional to the enthalpy and lamella thickness proportional to crystallization temperature as independent variables. This empirical method makes the approximate estimation of tensile modulus possible based on a simple calorimetric curve and shows that the principal structural parameters that influence the stiffness are crystallinity and lamella thickness. Despite its reasonably good accuracy, the empirical correlation provided by that study is applicable only in a limited crystallinity range, furthermore, the lamellar thickness parameter is time-consuming to determine [8].
Based on the results of Pukánszky et al., we developed an empirical model, which links the crystalline structure directly to the modulus in the entire crystallinity range. The model equation represents an S-type logistic function curve:

where, Ea and Ec are the tensile moduli for completely amorphous and perfectly crystalline polymers, respectively. X is the crystallinity, Tav is the average melting temperature, Tm0 is the equilibrium melting temperature, and α, β, γ are iterative empirical constants.
The most significant advantage of our model is that all the necessary information for the prediction of modulus can be gathered from a simple calorimetric measurement and the equation is valid in the entire crystallinity range. In our preceding studies, the model has been applied to numerous polymers such as iPP, PA, PLA, and PET. The iterative constants have been generated for these materials and consequently, tensile modulus values have been predicted. The obtained results showed good agreement with the experimentally determined values.
The research goals, open questions
The central aim of the research is to investigate the relationship between the structure and mechanical properties of semicrystalline polymers through the utilization of thermal analysis methods and the study of crystallization kinetics. Predictive models, like the one we developed, are important because if we have insights about how alterations in structure impact properties, it is possible to optimize processing conditions or additive formulations accordingly to enhance material performance and durability. Another significance of such models is that they can be beneficial to tailor materials with targeted properties without the need for extensive experimentation, thereby reducing the time and cost of the development process.
Regarding the functionality of our model, some of the open questions have been already addressed and examined. For instance, in a previous study, I investigated whether the use of different equipment, namely, a differential scanning calorimeter (DSC), affects the predicted results. The outcome was that for this model, power-compensated DSCs are more dependable than heat-flux ones. (see Fig. 1)
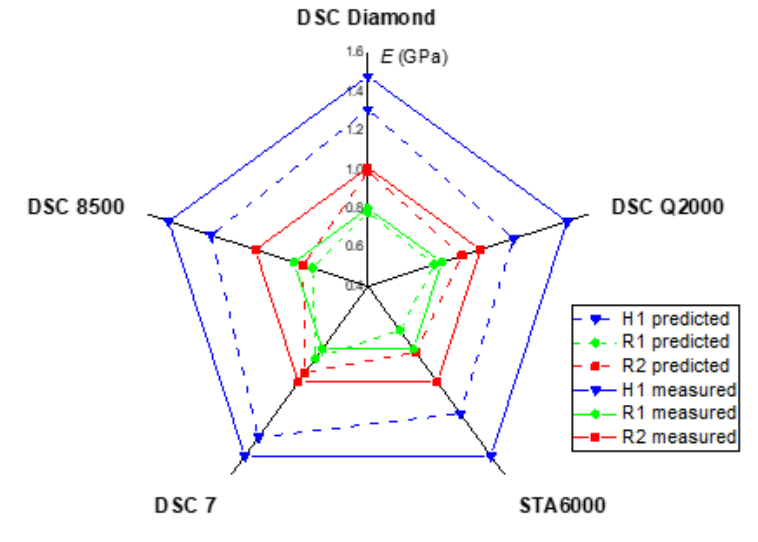
Fig.1 Visual representation of instrument dependency of the modulus estimations.
Another important condition is that the implemented instruments should be well-calibrated to obtain better estimates. One intriguing open question is that if the same protocol and procedures are followed by different researchers in different laboratories by using different equipment, will the results be the same or at least very similar? To have this question answered my main goal is to apply this empirical approach to various semicrystalline polymers and publish the results to promote the model so that it garners the attention of fellow researchers and is put into application by them as well. In the published papers, the detailed description of the entire procedure is described to make this approach reproducible and widely accessible to a wider audience. Moreover, it is worth mentioning that another challenge or open question is that there exists some ambiguity concerning the predictions at high crystallinity regions, which stems from the absence of experimental data points.
Methods
Standard dumbbell-shaped test specimens (ISO 527- 1:2019) were produced by using a DEMAG IntElect 560/330-100 type electronic injection molding machine. ISO 527 bars are preferred to repress the influence of the oriented skin, as within this type of specimen, mechanical characteristics are governed mostly by the core structure.
For the calorimetric measurements, small samples were taken by cutting from the core part of the dumbbell specimens. Hermetically sealed aluminum crucibles were utilized as sample holders and the mass of the cut pieces was 3–5 mg.
Melting and crystallization characteristics are analyzed by differential scanning calorimetry, typically by Perkin Elmer Diamond DSC apparatus. As a purge gas, a high-purity N2 atmosphere (20 mL min-1) is applied. The calorimeter has been calibrated by high-purity gallium, indium, and lead standard reference materials. Tensile modulus values are experimentally evaluated by employing an Instron 5566 type tensile testing machine (Instron, Germany) based on ISO 527-1:2019 standards. The gauge length is 115 mm, and the crosshead speed is 0.5 mm/min. Modulus values are measured below the 0.3% deformation range.
To predict the modulus, there are two important values to be evaluated first in the model equation given above. These quantities can be evaluated solely based on a single calorimetric measurement. One of these parameters is crystallinity (X). Once the melting curve is generated, the corresponding crystallinity value can be obtained by the ratio of the experimentally obtained enthalpy of fusion to the equilibrium enthalpy of fusion. The other parameter to be determined is average melting temperature (Tav) and it can be calculated directly from the melting curve by using the equation below:
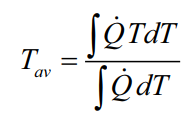
As it seems from the equation, the average melting point can be evaluated in two simple steps: The recorded heat flow curve is multiplied by temperature, and the area under the resulting curve is calculated. Then the obtained value is divided by the area under the simple heat flow curve. Additionally, iterative constants (α, β, γ) that are representative of the crystalline structure in the model equation, are estimated by fitting the model equation to tensile modulus – crystallinity data pairs in the entire crystallinity range. After obtaining the crystallinity and average melting temperature values from a single melting curve, along with the evaluated iterative constants, we can readily input these values into the model equation to estimate the modulus of the tested material. To finalize, the predicted values are always verified (validated) by using other grades of the same material that have different crystalline structures.
Results
So far, after applying this prediction model to several semicrystalline polymers (iPP, PLA, PET, PE), it can be confidently stated that a reasonably good agreement has been found between experimental and predicted modulus values. Comparison of predicted and experimentally measured modulus values are demonstrated in Fig. 2.
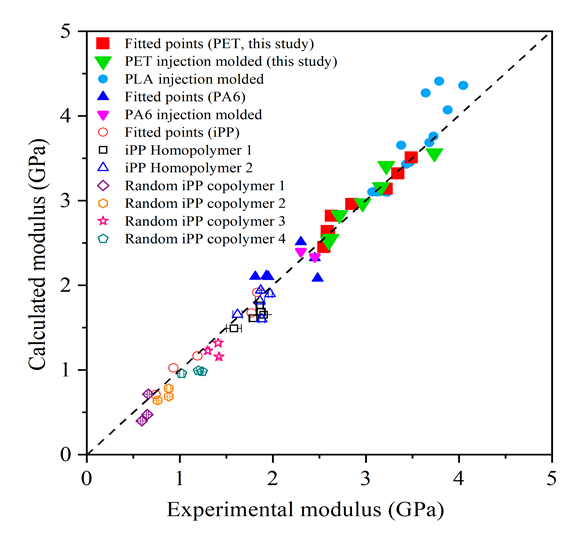
Fig. 2 Comparison of predicted and experimentally measured modulus.
I have conducted a robustness study for the model by using different DSC instruments and by applying two different versions of our model equation; one was an exponential function, and another was a logistic (sigmoidal) function. It was concluded that our logistic function not only gives good estimations but also makes the prediction of moduli in higher crystallinity ranges possible and always describes the expected sigmoid-type correlation, as shown in Fig. 3.
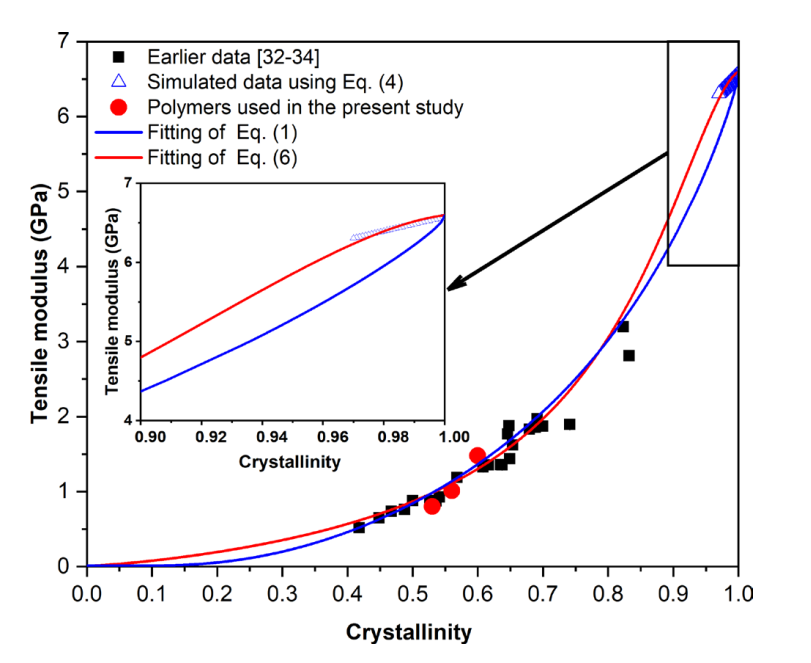
Fig. 3 Tensile modulus (E) as a function of crystallinity (X).
In my most recent study (which was published in a Q1 journal), I applied the model to PET, a polymer that undergoes cold crystallization. During the heating scan of PET in calorimetric analysis a cold crystallization peak emerges, originating from the crystallization of the amorphous regions. The cold crystallization process hinders the precise assessment of the calorimetric curves, as it is not possible to evaluate crystallinity from the enthalpy of fusion. The aim was to eliminate the cold crystallization and be able to proceed to estimate the modulus consequently. In this case, the average melting temperature value cannot be evaluated because cold crystallization alters the crystalline structure of the specimen and consequently its melting characteristics too. Thus, to evade this issue, melting curves were generated by applying higher heating rates which led to the elimination of cold crystallization (Illustrated in Fig. 4).
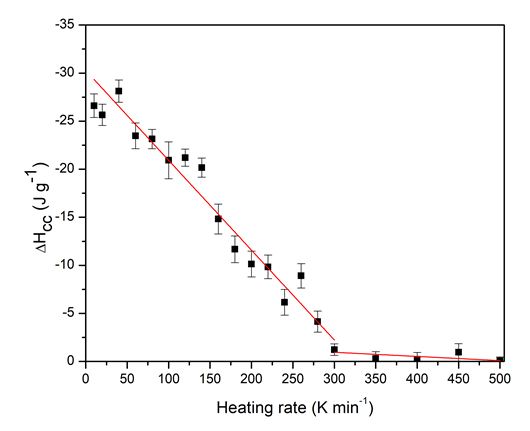
Fig. 4 ΔHcc as a function of heating rate.
Also, the influence of increasing the heating rate on cold crystallization behavior was examined. The results indicated that the prediction of tensile modulus is possible in polymers, which tend to cold crystallize similarly to other semicrystalline polymers.
Expected impact and further research
The enhancement of stiffness (tensile modulus) is a crucial issue in industrial practice. For instance, polypropylene grades have stiffness in the range of 1.5–2.5 GPa, which is much smaller than the calculated 6.6 GPa. Recently, the desired limit value to be exceeded is 3 GPa. Using our simple equation, the crystalline structure necessary to fulfill this need can be predicted, if we simulate the modulus using fixed crystallinity or lamella thickness data. The fundamental importance of the model is that it can have a remarkably positive effect on tailoring properties, improvement of material performance as well as the limitations of a material’s potential. My further research in this field will focus on expanding the scope of the empirical model to investigate more polymers and have more insights into their reliability and potential. As of now, I am working with polyamides where I am examining how the moisture content of the material (humidity) affects the tensile modulus predictions. Furthermore, another main objective is to compile a comprehensive review of our model by summarizing all the findings and results of various polymer studies to provide a thorough overview of its effectiveness.
Publications, references, links
List of corresponding own publications:
[AZ 1] A. Zarbali, B. Pinke, A. Menyhárd, Robustness study of a tensile modulus prediction model for semicrystalline polymers, Period. Polytech. Chem. Eng. 67 (2023) 232–241. https://doi.org/10.3311/PPch.20991.
[AZ 2] A. Zarbali, I. Djaffar, A. Menyhárd, Prediction of tensile modulus based on parameters of crystalline structure in polyethylene terephthalate with cold crystallization ability, Heliyon. 10 (2024). https://doi.org/10.1016/j.heliyon.2024.e26122.
[AZ 3] A. Zarbali, Y. Yosser, A. Menyhárd, Estimation of tensile modulus of polyethylene based on single calorimetric curves (manuscript ready)
Table of links:
Differential Scanning Calorimetry
List of references:
[1] E.P. Moore, Polypropylene Handbook: Polymerization, Characterization, Properties, Processing Applications, Hanser/Gardner Publications, Cincinnati OH, 1996
[2] V. A. Sedighiamiri, T.B. Erp, van, G.W.M. Peters, L.E. Govaert, J.A.W. Dommelen, Micromechanical Modeling of the Elastic Properties of Semicrystalline Polymers: A Three-Phase Approach, J. Polym. Sci. Part B Polym. Phys. 48 (2010) 2173–2184
[3] D.R. Breese, G. Beaucage, A review of modeling approaches for oriented semi-crystalline polymers, Curr. Opin. Solid State Mater. Sci. 8 (2004) 439–448
[4] T.D. Horn, D. Heidrich, H. Wulf, M. Gehde, J. Ihlemann, Multiscale simulation of semicrystalline polymers to predict mechanical properties, Polymers (Basel). 13 (2021) 1–16
[5] O. Gueguen, S. Ahzi, S. Belouettar, A. Makradi, Comparison of micromechanical models for the prediction of the effective elastic properties of semicrystalline polymers: Application to polyethylene, Polym. Sci. - Ser. A. 50 (2008) 523–532
[6] A. Menyhárd, P. Suba, Z. László, H.M. Fekete, O. Mester, Z. Horváth, G. Vörös, J. Varga, J. Móczó, Direct correlation between modulus and the crystalline structure in isotactic polypropylene, Express Polym. Lett. 9 (2015) 308–320
[7] B. Pukánszky, I. Mudra, P. Staniek, Relation of Crystalline Structure and Mechanical Properties of Nucleated Polypropylene, J. Vinyl Addit. Technol. 3 (1997) 53–57
[8] J. Molnár, A. Hertner-Horváth, A. Menyhárd, Prediction of tensile modulus from calorimetric melting curves of polylactic acid with pronounced cold crystallization ability, Polym. Test. 95 (2021)
