Fizikai Tudományok Doktori Iskola 

TTK, Fizika Tanszék

Témavezető: Dr. Halbritter András

Memrisztorok kísérleti vizsgálata és neuromorfikus alkalmazásai

A kutatási téma néhány soros bemutatása

Kutatásom fókuszában nanométeres méretskálájú rezisztív kapcsolómemóriák fejlesztése és fizikai folyamatainak tanulmányozása áll. További célom ezen eszközök felhasználásával neuromorfikus jelfeldolgozó hálózatok létrehozása.

A kutatóhely rövid bemutatása

A rezisztív kapcsolómemóriák fejlesztéséhez szükséges mind az Energiatudományi Kutatóközpontban található Műszaki Fizikai és Anyagtudományi Intézet Nanoérzékelők Laboratóriumának nanofabrikációs eszközparkja, mind a BME Fizika Tanszékén az Atomi- és Molekuláris Elektronika Kutatócsoport egyedi tervezésű mérőrendszerei. Az egyetemi kutatólaboratóriumban található héliumcseppfolyósító rendszernek köszönhetően lehetőség nyílik alacsony hőmérsékletű szupravezető spektroszkópiás vizsgálatokra is.

A kutatás történetének, tágabb kontextusának bemutatása

A rezisztív kapcsolómemóriák – más néven memrisztorok – általánosan olyan fém-szigetelő-fém nanostruktúrák, amelyek vezetőképességét az eszköz elektródáira kapcsolt elektromos jelekkel változtatni lehet, információt tárolva a memrisztor vezetőképességében [1]. A rezisztív kapcsolás során egy nanométeres – bizonyos esetekben akár atomi [S1] – méretskálájú vezető csatorna (filamentum) alakul ki az eszköz aktív tartományában, amelyhez számtalan fizikai mechanizmus hozzájárulhat a memrisztor anyagstruktúrájától függően [2]. Néhány lehetséges kapcsolási jelenséget mutat az 1. ábra. A rezisztív kapcsolás nem illékony változatainak feszültség- és időfüggő dinamikáját kihasználva többszintű (analóg) programozás is megvalósítható (1.a ábra) [S1,S3-S5,T1]. Ezen rezisztív kapcsolómemóriák ígéretes platformot szolgáltatnak például mesterséges neurális hálózatok nagyméretű szinaptikus súly-mátrixainak hardverszintű kódolására [3-4]. Másfajta memrisztorok illékony memóriával rendelkeznek (1.b ábra) [S2], és alkalmazhatóak neurális jelgenerálási feladatokra mesterséges neuronként vagy oszcillátorként [5]. Hasznosítva a különféle memrisztorok kapcsolásdinamikai tulajdonságait, hardverszinten működő jelfelismerési és -feldolgozási feladatok megvalósíthatóak mindössze néhány eszköz felhasználásával [T2-T3]. A memrisztorok ellenállással együtt hangolható zajkarakterisztikájának [S6] köszönhetően kiválóan alkalmasak lehetnek probabilisztikus elvű számítási algoritmusok hardveres megvalósítására [6,T4]. A számítási és hosszútávú memóriafunkciók egyesítésével, túllépve a Neumann-architektúrák korlátait, a rezisztív kapcsolómemóriák a jövő egyik legperspektivikusabb fejlődési irányát jelentik az új információs technológiák területén [7].

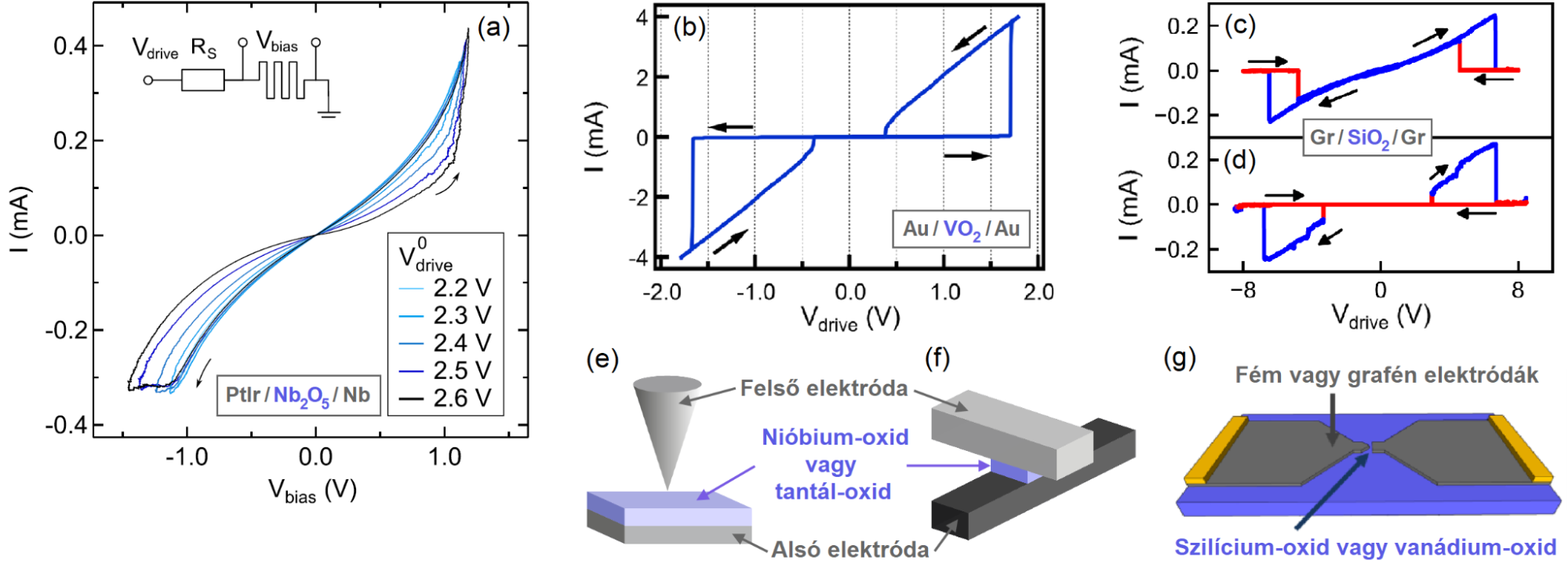
1. ábra: Különböző memrisztorok (a–d) áram-feszültség karakterisztikái és (e–g) tipikus struktúrájának rajzai. [S1-S4]

A kutatás célja, a megválaszolandó kérdések

Kutatómunkám egyik fő célja különféle rezisztív kapcsolómemóriák fizikai folyamatainak feltárása és modellezése (kvantumtranszport-tulajdonságok és sztochaszticitás), másrészt fontos törekvés olyan on-chip eszközök fejlesztése is, amelyek alkalmasak lehetnek komplex jelek feldolgozására, hasznosítva az eszközök belső fizikai működését.

Az aktív tartomány mérete és skálázhatósága technológiai szempontból kritikus tulajdonságok, viszont a kialakuló nanofilamentumok egyedi szerkezetének feltárása, in-situ, roncsolásmentes kísérleti vizsgálata nehéz feladat. Elektronmikroszkópiás módszerekkel lehetséges a filamentumok leképezése [8,9], ám egy vertikális struktúrájú memrisztor (1.f-e ábra) működésének vizsgálata ezekkel az eljárásokkal korlátozott. Kutatásom során ezért egy szupravezető spektroszkópiás módszert ültettem át Nb₂O₅- és Ta₂O₅-alapú memrisztorok vizsgálatára, amelyet korábban széles körben alkalmaztak atomi vezetékek kvantumtranszport-tulajdonságainak feltérképezésére [10].

A memrisztorok működése eredendően sztochasztikus természetű, ami megjelenik az eszközök több mérhető fizikai jellemzőjén keresztül. Ilyen például a ciklikus mérések során tapasztalt ellenállás-állapotok és kapcsolási idők variabilitása. Utóbbi mennyiségek korrelációi és a kapcsolási idők fluktuációjának eloszlása értékes információkkal szolgál a mögöttes mechanizmusról. Célom feltárni ezen mennyiségek vizsgálatán keresztül SiO₂-alapú rezisztív kapcsolómemóriák működésének részleteit, különös tekintettel a nukleációs elmélet [11] alkalmazhatóságára.

Módszerek

Mintakészítés

Kutatómunkám kezdetén főként pontkontaktusok vizsgálatával foglalkoztam, amelyeket STM (scanning tunneling microscope) elrendezésben hoztam létre egy tű segítségével egy rezisztív kapcsoló vékonyréteg (Nb₂O₅ vagy Ta₂O₅) felületén (1.e ábra). Ezen technika előnye, hogy egyszerű az újabb kontaktusok létrehozása a tű ismételt felemelésével és kontaktálásával egy másik lokáción. Ezekhez a kísérletekhez a rezisztív kapcsoló vékonyrétegeket a készen kapott hordozó fémrétegek felületén anódos oxidációval hoztam létre [S1,S5-S6]. Az STM pontkontaktus technika egyik hátránya, hogy egy-egy kontaktus rövid életű, mindössze az STM rendszer ~10 perces időskáláján stabil. Másik limitáció, hogy ezek a pontkontaktusminták nem integrálhatóak. Ezért fontos célunk volt olyan on-chip memrisztorok fejlesztése, amelyek skálázhatóság szempontjából megfelelnek a technológiai elvárásoknak. Ilyen on-chip memrisztorok elektronsugár-litográfiás módszerrel történő előállításában és a gyártási módszerek optimalizálásában részt vettem az utóbbi évek folyamán [S2-S3,S6]. Az elektronsugár-litográfia és a vékonyréteg-leválasztás technikáit az EK MFA Nanoérzékelők Laboratóriumában sajátítottam el Dr. Pósa László segítségével.

 

Szupravezető spektroszkópia

Egy atomi vezeték vezetőképességét kifejezhetjük a Landauer-formulával, , ahol _i az elektrontranszport valószínűsége az i. csatornában, M a vezetési csatornák száma és G₀ = 2e²/h a vezetőképesség kvantuma. A transzmissziós sajátértékek kísérleti úton történő meghatározására egy különleges módszer a szupravezető subgap spektroszkópia, amelynek lényege a szupravezető energiarés-tartományában mért áram-feszültség karakterisztikák illesztése [12]. Ezzel a módszerrel demonstráltam, hogy Nb₂O₅ memrisztorokban kialakulhatnak mindössze egyetlen atom átmérőjű filamentumok [S1]. Olyan átmenetifém-kontaktusok esetén, amelyek már 2 – 3 atomból állnak, 10 – 15 vezetési csatorna a realisztikus, a sok vegyértékelektron jelenléte miatt [10]. Ezek a diffúzív nanovezetékek jól modellezhetőek randommátrix-elméleti számításokból származó univerzális transzmisszió-eloszlással [13]. Yu. V. Nazarov munkája alapján egy kiterjedt hibahely jelenléte hatással van a transzmisszió-eloszlásra, ami pontosan modellezhető az  = R_vezeték/R_hibahely paraméter függvényében [14]. Az elmélet alkalmazásával feltárulnak a Ta₂O₅-alapú memrisztorok kvantumtranszport-tulajdonságai [S4].

 

Eddigi eredmények

Szupravezető spektroszkópia Nb₂O₅ és Ta₂O₅ memrisztorokon

A rezisztív kapcsolómemóriákban létrehozható legkisebb aktív tartomány után kutatva, először Nb₂O₅-alapú pontkontaktus-memrisztorokat (2.a ábra) vizsgáltam. A kapcsolási görbe (2.b ábra) állapotaiban megállva, alacsony jelszintű (~10 mV) subgap-karakterisztikák mérésével bebizonyosodott, hogy egyetlen domináns csatorna () alkotja a G₀ körüli ON állapotokat (2.c ábra). Ezen mérések elsőként bizonyították valódi egyatomos vezetési csatornák jelenlétét átmenetifém-oxid memrisztorokban [S1].

 

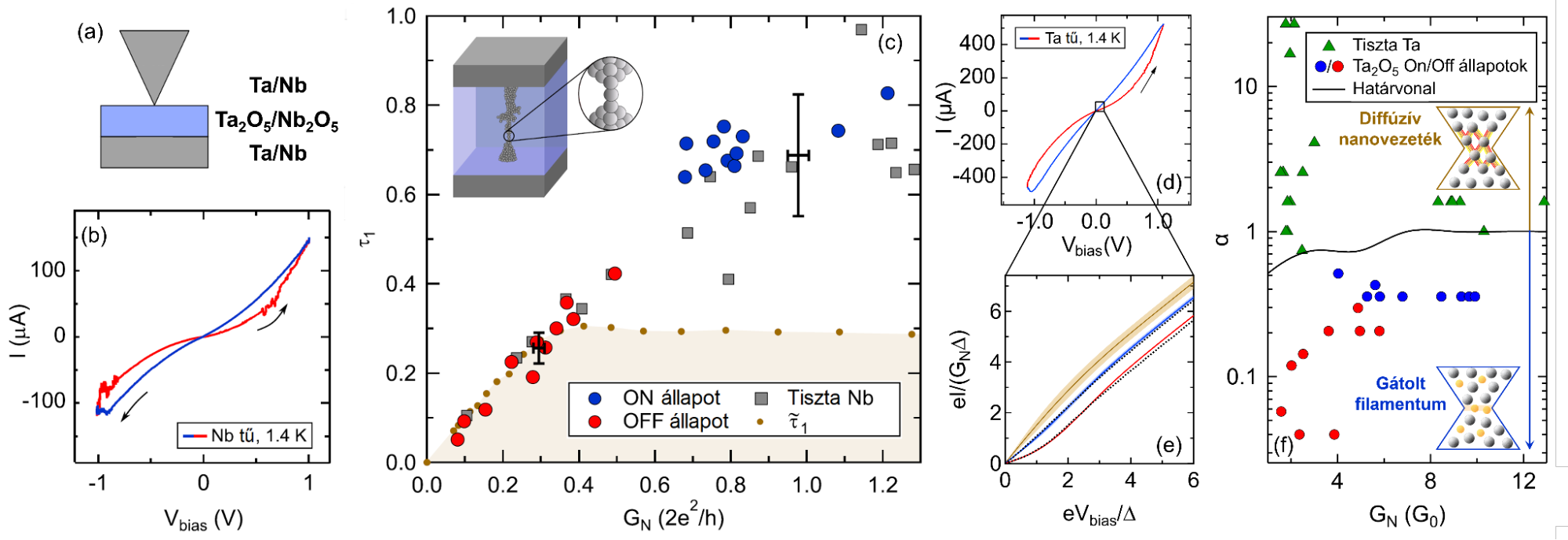
2. ábra: (a) STM pontkontaktus rajza. (b) Rezisztív kapcsolás 1,4 K hőmérsékleten Nb/Nb₂O₅/Nb kontaktuson. (c) Az első vezetési csatorna transzmissziója atomi kontaktust jelez a G₀ környéki ON állapotokban. (d) Rezisztív kapcsolás és (e) subgap karakterisztikák 1,4 K hőmérsékleten Ta/Ta₂O₅/Ta kontaktuson. (f) A kiterjedt hibahely  paramétere a vezetőképesség függvényében;  értékének megfelelő modellek illusztrációja a határvonal két oldalán. [S1,S4]

 

Vizsgálataimat kiterjesztettem nagyobb vezetőképességű tartományban (2–10 G₀) működtetett Ta₂O₅-alapú memrisztorokra (2.d ábra). Itt már szükséges transzmisszió-eloszlásokkal modellezni a kontaktust a subgap-karakterisztikák illesztéséhez (2.e ábra). Az ON/OFF állapotokban (2.e kék/piros görbe) eltéréseket tártam fel a tiszta, diffúzív nanovezeték modelljéhez képest (2.e barna görbe). A memrisztor-állapotokban egy kiterjedt hibahely gátolja a filamentumban a transzportot, ami kivehető az illesztésekből kapott _ON,OFF < 1 tendenciából (2.f ábra) [S4].

 

Sztochasztikus nukleáció SiO₂ memrisztorokban

A SiO₂-alapú nanorésmemrisztorok (3.a–b ábra) [15] bekapcsolási időeloszlásának statisztikai elemzésével feltártam, hogy a bekapcsolás leírható nukleációs folyamatként [S3]. A modell lényege egy ciklusonként véletlenszerűen változó nukleációs energiagát, amelynek korrelációs paramétere 200 kapcsolási ciklus. Az ennél hosszabb sorozatok hisztogramja lognormális (3.d ábra), míg a rövidebb sorozatoké exponenciális (3.e ábra) eloszlást mutat.

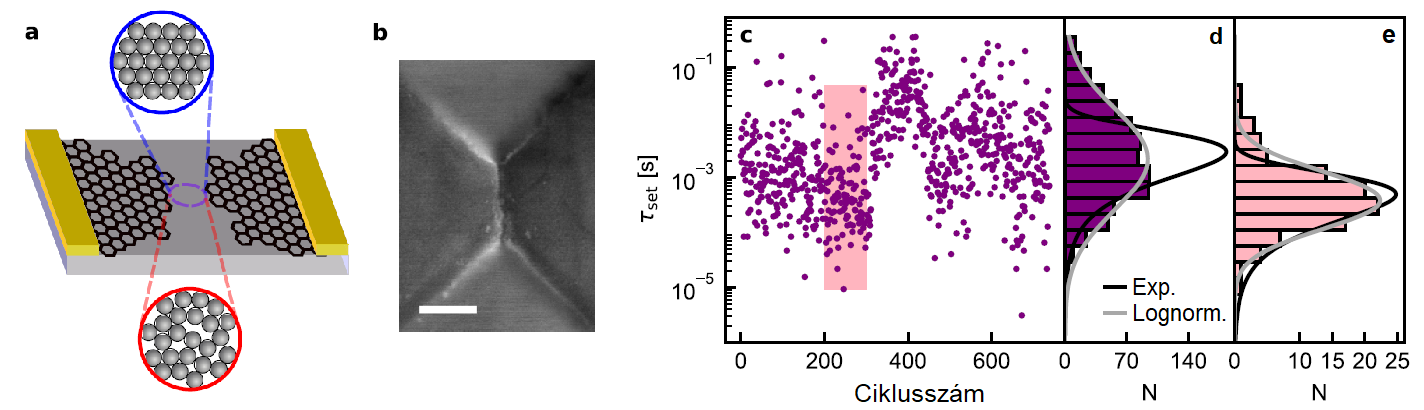
3. ábra: (a) Gr/SiO₂/Gr nanorésminta és az ON/OFF állapotok kristályos/amorf szerkezetének rajza. (b) Pásztázó elektronmikroszkópos felvétel az aktív tartományról, skála: 200 nm. (c) A bekapcsolási idő evolúciója Gr/SiO₂/Gr memrisztorokban. (d) A teljes adatsor, illetve (e) egy korlátozott hosszúságú adatsor hisztogramja. [T1,S3]

 

Memrisztoralapú neuromorfikus áramkörök

Egy kis jelszinten előfeszített Ta₂O₅ memrisztor képes zajos környezetben bizonyos mintázatokat felismerni, ugyanis bemenetén egy rövid tüske csak rövidtávú, viszont egy hosszabb impulzus maradandó ellenállásváltozást okoz. Az áramkört kiegészítve egy általunk készített VO₂ memrisztoralapú oszcillátorral, egy autonóm neurális tüskedetektor/jeladó egység valósítható meg (4.a ábra) [T2,S7]. Ugyanezt az oszcillátor-egységet egy piezoelektromos rezgőnyelv kimenetére kapcsolva (4.b ábra) mesterséges hangérzékelő-egységet létesíthetünk, amely a természetes halláséhoz hasonló karakterisztikákat mutat [T3].

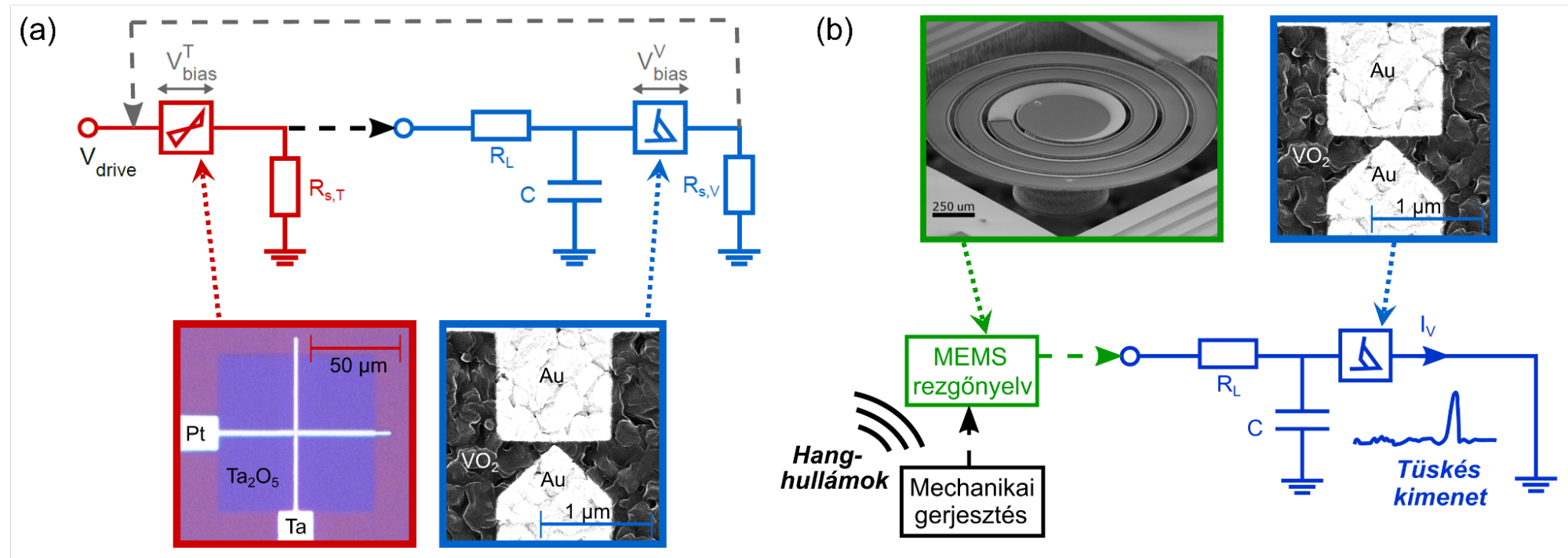
4. ábra: (a) Neurális tüskedetektor/jeladó egység Ta₂O₅ és VO₂ memrisztorokból. [T2,S7] (b) Mesterséges hangérzékelő-egység koncepciója egy piezoelektromos rezgőnyelv [16] és egy VO₂ memrisztor összekapcsolásával. [T3]

Várható impakt, további kutatás

A továbbiakban nagy hangsúlyt kap a memrisztorok kapcsolás-dinamikai tulajdonságainak eszköz-szintű alkalmazása, többek között a [T2] és [T3] munkák alapján készülő publikációk (pl. [S7]) által. Ezen kívül célunk ultragyors (f_osc. > 10 MHz), VO₂-alapú oszcillátorok fejlesztése [17,18]. További cél memrisztorok hangolható zajkarakterisztikáját [S6] hasznosító sztochasztikus optimalizációs eljárások megvalósítása [T4,19].

 

Saját publikációk, hivatkozások, linkgyűjtemény

Kapcsolódó saját publikációk listája.

 

[S1] Tímea Nóra Török, Miklós Csontos, Péter Makk, András Halbritter. Breaking the Quantum PIN Code of Atomic Synapses. Nano Letters 20, 1192–1200 (2020)

 

[S2] László Pósa, Péter Hornung, Tímea Nóra Török, Sebastian Werner Schmid, Sadaf Arjmandabasi, György Molnár, Zsófia Baji, Goran Dražić, András Halbritter, János Volk. Interplay of Thermal and Electronic Effects in the Mott Transition of Nanosized VO₂ Phase Change Memory Devices. ACS Applied Nano Materials 6, 9137–9147 (2023)

 

[S3] Tímea Nóra Török, János Gergő Fehérvári, Gábor Mészáros, László Pósa, András Halbritter. Tunable, Nucleation-Driven Stochasticity in Nanoscale Silicon Oxide Resistive Switching Memory Devices. ACS Applied Nano Materials 5, 6691–6698 (2022)

 

[S4] Tímea Nóra Török, Péter Makk, Zoltán Balogh, Miklós Csontos, András Halbritter. Quantum Transport Properties of Nanosized Ta₂O₅ Resistive Switches: Variable Transmission Atomic Synapses for Neuromorphic Electronics. https://pubs.acs.org/doi/10.1021/acsanm.3c04769 (2023)

 

[S5] Dániel Molnár, Tímea Nóra Török, Botond Sánta, Agnes Gubicza, András Magyarkuti, Roland Hauert, Gábor Kiss, András Halbritter, Miklós Csontos In situ impedance matching in Nb/Nb₂O₅/PtIr memristive nanojunctions for ultra-fast neuromorphic operation. Nanoscale 10, 19290–19296 (2018)

 

[S6] Botond Sánta, Zoltán Balogh, László Pósa, Dávid Krisztián, Tímea Nóra Török, Dániel Molnár, Csaba Sinkó, Roland Hauert, Miklós Csontos, András Halbritter. Noise Tailoring in Memristive Filaments. ACS Applied Materials & Interfaces 13, 7453–7460 (2021)

 

[S7] Dániel Molnár, Tímea Nóra Török, Roland Kövecs, László Pósa, Péter Balázs, Zoltán Balogh, György Molnár, Nadia Jimenez Olalla, Juerg Leuthold, János Volk, Miklós Csontos, András Halbritter. Autonomous neural information processing by a dynamical memristor circuit. Elérhető: https://arxiv.org/abs/2307.13320

 

 

Témavezetői tevékenység.

 

[T1] Fehérvári János Gergő. Nanoméretű fázisváltó memóriák időskáláinak kísérleti vizsgálata. Kari TDK dolgozat (2020)

 

[T2] Kövecs Antal Roland. Neurális dinamikával rendelkező memrisztoralapú detektoráramkör megvalósítása. Kari TDK dolgozat (2022)

 

[T3] Kövecs Antal Roland. Memrisztoralapú jelfeldolgozó egység tervezése cochleáris implantátumokhoz. Szakdolgozat (2023)

 

[T4] Fehérvári János Gergő. Sztochasztikus jelenségek rezisztív kapcsoló memóriákban. Szakdolgozat (2021)

 

 

Linkgyűjtemény.

 

EK MFA Nanoérzékelők Laboratórium

BME Fizika Tanszék

Transzport nanovezetékekben

International Roadmap for Devices and Systems (IRDS™) 2022. évi jelentése

Szabadalmak memrisztor témában

 

 

Hivatkozások listája.

 

[1] M. A. Zidan et al. The future of electronics based on memristive systems. Nature Electronics 1, 22–29 (2018)

 

[2] Z. Wang et al. Resistive switching materials for information processing. Nature Reviews Materials 5, 173–195 (2020)

 

[3] S. Ambrogio et al. Equivalent-accuracy accelerated neural-network training using analogue memory. Nature 558, 60–67 (2018)

 

[4] Q. Xia, J. J. Yang. Memristive crossbar arrays for brain-inspired computing. Nature Materials 18, 309–323 (2019)

 

[5] W. Yi et al. Biological plausibility and stochasticity in scalable VO₂ active memristor neurons Nature Communications 9, 4661 (2018)

 

[6] F. Cai et al. Power-efficient combinatorial optimization using intrinsic noise in memristor Hopfield neural networks. Nature Electronics 3, 409–418 (2020)

 

[7] International Roadmap for Devices and Systems (IRDS™), 2022 Edition: Beyond CMOS and Emerging Materials Integration

 

[8] Y. Yang et al. Observation of conducting filament growth in nanoscale resistive memories. Nature Communications 3, 732 (2012)

 

[9] D.-H. Kwon et al. Atomic structure of conducting nanofilaments in TiO₂ resistive switching memory. Nature Nanotechnology 5, 148–153 (2010)

 

[10] E. Scheer et al. The signature of chemical valence in the electrical conduction through a single atom contact. Nature 394, 154 (1998)

 

[11] V. G. Karpov et al. Field-induced nucleation in phase change memory. Phys. Rev. B 78, 052201 (2008)

 

[12] N. Agrait et al. Quantum properties of atomic-sized conductors. Physics Reports 377, 81 (2003).

 

[13] C. W. J. Beenakker. Random-matrix theory of quantum transport. Reviews of Modern Physics 69, 731–808 (1997)

 

[14] Yu. V. Nazarov. Limits of universality in disordered conductors. Phys. Rev. Lett. 73, 134–137 (1994)

 

[15] L. Pósa et al. Multiple Physical Time Scales and Dead Time Rule in Few-Nanometers Sized Graphene-SiO_x-Graphene Memristors. Nano Letters 17, 11, 6783–6789 (2017)

 

[16] P. Udvardi et al. Spiral-Shaped Piezoelectric MEMS Cantilever Array for Fully Implantable Hearing Systems. Micromachines 8, 311 (2017)

 

[17] Md. Suruz Mian et al. Self-oscillation up to 9 MHz based on voltage triggered switching in VO₂/TiN point contact junctions. Journal of Applied Physics 117, 215305 (2015)

 

[18] B. Zhao et al. Low-Power Microwave Relaxation Oscillators Based on Phase-Change Oxides for Neuromorphic Computing. Physical Review Applied 11, 014020 (2019)

 

[19] Fehérvári János Gergő. Sztochasztikus optimalizáció hangolható zajforrásként működő memrisztorok segítségével. Kari TDK dolgozat (2022)