Pal Csonka Doctoral School 

BME Építészmérnöki Kar, Department of Morphology and Geometric Modeling, ELKH-BME Morphodynamics Research Group

Supervisor: Dr. Domokos Gábor

Space-filling tilings as geometrical models

Introducing the research area

We are surrounded by space-filling patterns every day: just think of the patterns visible on a masonry wall, a map, a beehive, or a cracked rock surface. In my work, I examine these natural and artificial patterns through the lens of discrete geometry. The advantage of the mathematical description is that it reveals general relationships that allow us to infer the past or even the future of such patterns. Currently, I am collaborating with researchers from the University of Pennsylvania to study crack patterns captured on celestial bodies in the Solar System and with researchers from the University of Bern and Shanghai to study molecular patterns observable through scanning tunneling microscope. It is fascinating to see that, although the scales differ greatly, geometric models work effectively in both cases.

The work described in this current proposal was conducted and is being carried out beyond my doctoral research (which focuses on the examination of mechanical equilibria of convex polyhedra).

 

Brief introduction of the research place

I conduct my research as a member of the ELKH-BME Morphodynamics Research Group. The main focus of the group is the mathematical and physical modeling of forms and patterns appearing in nature and artificial environments, with applications in geophysics, planetology, urban planning, and chemistry. Together with several members of the research group, I work at the Department of Morphology and Geometric Modeling, where we teach geometric topics related to architecture.

 

History and context of the research

Space-filling patterns have always appeared in a broad variety of natural phenomena, but even in the man-made environment, there are examples dating back more than twenty thousand years, as we can find such ancient masonry structures [B2]. With the development of transportation, road networks emerged [B4], which drew space-filling planar patterns on maps. The use of discrete elements to create two-dimensional spatial fillings also appears as an artistic tool, and we can cite numerous ancient mosaics as examples [B5]. Walls are one of the oldest structures in architecture [B2] and they take us one dimension higher as their elements - with small gaps - fill the three-dimensional space.

It is not only the space-filling patterns that have been part of human culture for millennia, but their geometric descriptions also date back at least 2500 years. In Plato's notable theory, he identified the five regular (Platonic) solids with the five Elements, and this theory still influences certain areas of scientific thinking.

In the article [B6], Plato's hypothesis regarding the cube in his aforementioned theory was tested in a fascinating experiment: by approximating 556 dolomite fragments with convex polyhedra, the authors obtained average face and vertex numbers of (6.03, 8.01), which approximate the values belonging to the cube (6, 8) remarkably well. Using geometric tools, they also demonstrated that this numerical agreement is not a result of pure chance.

 

The research goals, open questions

The geometry of space-filling patterns raises numerous interesting mathematical questions. For example, we can ask the minimal number of sharp vertices that a two- or three-dimensional space-filling cell must have. Our aim is to develop the mean-field theory of mosaics through the investigation of similar questions. Another objective is to explore the potential applications of this theory.

In various application areas such as geology, chemistry, and urban planning, we can establish geometric models predicting the time evolution of patterns. Our goal is to provide model-based explanations for the current state and temporal evolution of patterns, collaborating with researchers from different scientific fields and utilizing geometric tools.

Among other things, we would like to examine the following questions: Can we infer the past and predict the future of geological crack networks based on the visible current patterns? What can we say about the same issue regarding city map networks? Can we estimate the geometry of molecular patterns based on the structure of the molecule and observed scanning tunneling microscope images? Can the mean-field theory of space-filling patterns be applied in other areas?

 

Methods

 

We model the patterns using so-called normal tilings. These consist of cells that fill the space without gaps, and they can only overlap on edges and vertices (nodes). Normal tilings also satisfy additional conditions [A1]. The number of vertices associated with a single cell is denoted by v, and it is called the combinatorial degree of the cell, while the number of overlapping cells at a node is denoted by n, and it is referred to as the combinatorial degree of the node [B1]. However, these measures are only sensitive to the combinatorial properties of the mosaic and do not tell us anything about the shape of the cells. Therefore, we introduced the nodal corner degree n* and the cell corner degree v* [A1]. These differ from the previous quantities in that they do not consider the 180° angles either between the vertices of a cell or between the sharp angles at the nodes. If a node does not have any 180° angles, it is called regular, otherwise, it is called irregular (Figure 1).

 

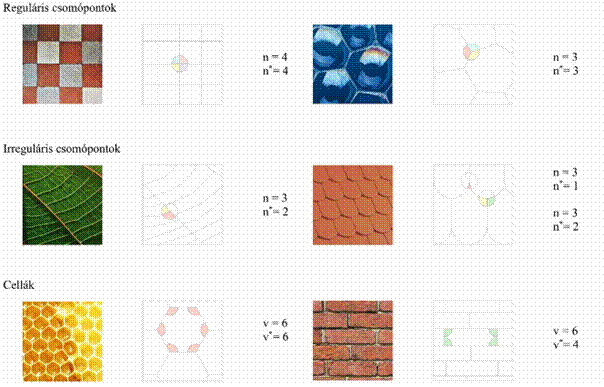
Figure 1. Examples of determining node and cell degrees.

 

The quantities above characterize a mosaic with the averaged values of  and  relative to the entire space (on which the pattern is situated). Based on these quantities, we can position the mosaics on the [] metric symbolic plane (Figure 2).

 

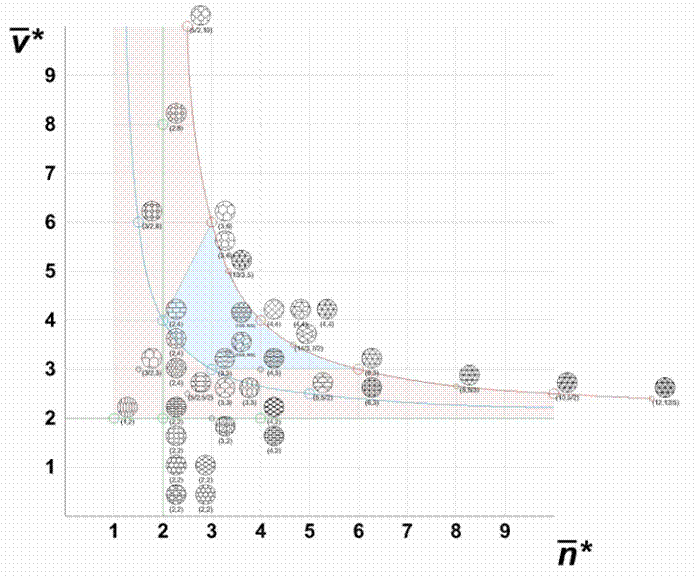
Figure 2. Periodic tilings on the metric symbolic plane.

 

The time evolution of geological fracture patterns was modeled using a discrete sequence of local steps. We can assign changes in the cell and nodal degrees to these experimentally validated geological steps. An example of such a step is the splitting of a cell, which results in the creation of 1 new cell, 2 new nodes, and 1 new edge. By associating probabilities to these steps and examining the mosaic within a circle whose radius approaches infinity, the model (when using a suitable random process for the timing of discrete steps) becomes continuous in time, and the time evolution of the fracture network is characterized by smooth trajectories on the symbolic plane, typically exhibiting attracting limit points which are particularly interesting from a geological perspective.

 

We also applied the mean-field theory of mosaics to monolayer molecular patterns. In this case, we analyzed the different patterns observed at various magnifications and separated them into distinct categories, so-called levels: The lowest level (level 1) is the molecule itself, for which we have geometric and chemical information, while the highest level (level 4) is the image visible through a scanning tunneling microscope, where we identified individual molecules as nodes (Figure 6). Based on the available information from these two situations, we made estimates for the intermediate levels which are neither known from the theoretical end, nor are they visible by any microscope, but are currently one of the hottest areas in material science.

 

Results

 

The previously raised question regarding the minimum number of vertices of a 2-dimensional space-filling cell was answered in [A1]. Based on the proof we provided with my co-authors, the answer is 2, and in three dimensions we showed that the lower bound is 0. To prove the 2-dimensional case, we devised a so-called deregularization algorithm, which transforms patterns by creating irregular vertices as we move further away from their regular state (Figure 3).

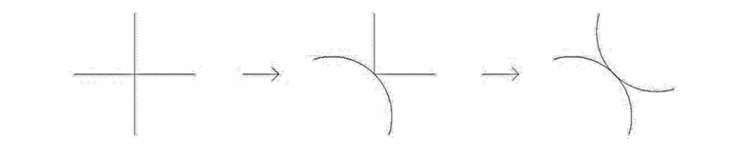
Figure 3. The deregularization algorithm.

 

In [B6], a general model for primary fracture patterns is discussed. Based on this, in [A2], we formulated a discrete evolution model containing two steps. Step R0 represents secondary fractures, while step R1 involves a rearrangement of fractures where "T" nodes transform into "Y" nodes (Figure 4).

 

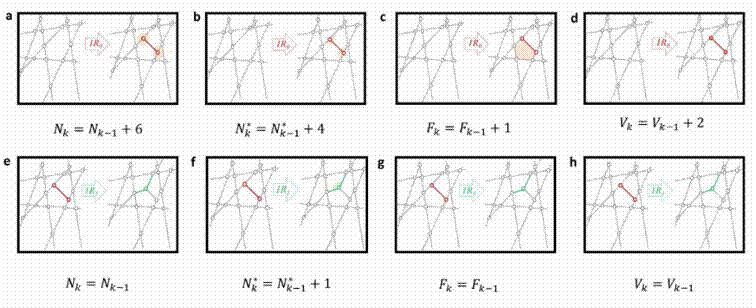
Figure 4. Changes in a mosaic for R0 (a, b, c, d) or R1 (e, f, g, h) steps. N denotes the number of angles, N* denotes the number of angles different from 180°, F denotes the number of faces, and V denotes the number of vertices.

 

Based on the above, the limit point for discrete dynamics can be determined as ,, where p is the probability of step R1, and (1-p) is the probability of step R2. By using the dynamics, trajectories describing the evolution of the mosaic can be plotted on the symbolic plane for any given probability p (Figure 5).

 

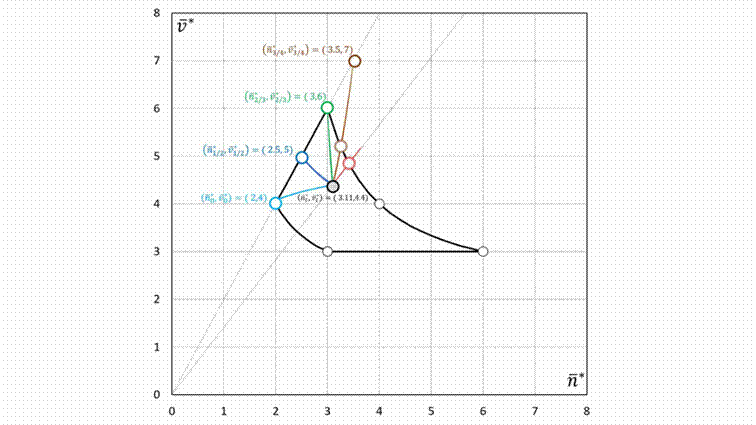
Figure 5. Numerical simulations for various values of p (p = 0, 1/2, 2/3, 3/4, 1). Trajectories with the initial mosaic () = (3.11, 4.4).

 

This model was further developed into a continuous-time model in the manuscript [A4].

 

In [A3] we investigated monolayer supramolecular patterns with hydrogen bonding. Currently, with the available tools (e.g., scanning electron microscope), the precise structure of materials cannot be fully determined with the desired accuracy. Extensive supercomputer calculations are required for this purpose. Using a geometric method, we managed to formulate exact estimations for the range unobservable with a microscope (Figure 6).

 

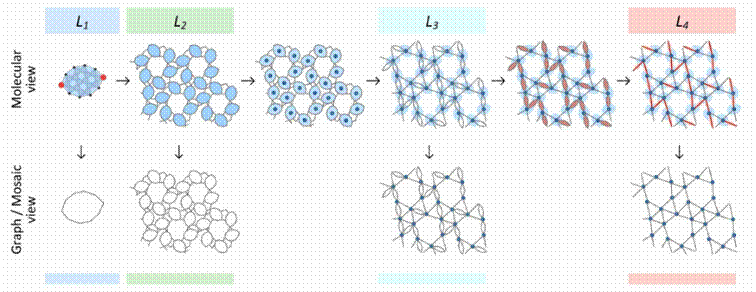
Figure 6. Illustrations of levels (L1, 2, 3, and 4) through the example of molecule 2,7-pyrenedione.

 

Since these molecular mosaics are all regular, they are positioned on the hyperbola . Therefore, it is sufficient to estimate either the nodal or the cell degree. The estimates define regions on the symbolic plane that lie on the hyperbola (Figure 7).

 

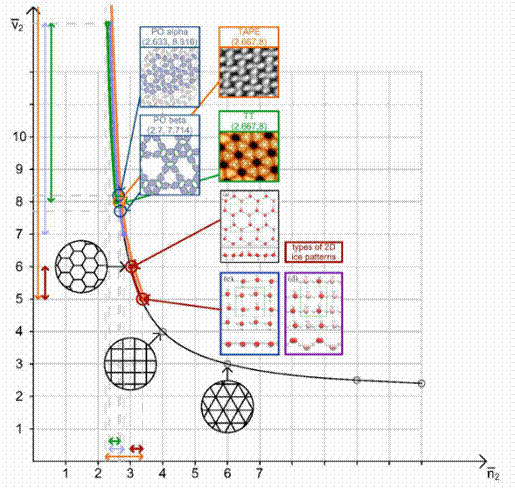
Figure 7. Level 2 patterns on the symbolic plane with their predicted ranges. The patterns of 2-dimensional ice appear at both ends of the determined region.

 

As seen in Figure 7, there are materials whose ranges do not coincide. We refer to these as combinatorially disjoint materials. We also found a molecule that appears with patterns corresponding to both ends of the estimated region. This implies that our estimates are sharp and cannot be improved.

 

Expected impact and further research

 

From a theoretical perspective, the geometric examination of 3-dimensional patterns and the further development of their mean-field theory is an interesting question. It is fascinating how the language of geometry can establish connections between seemingly distant phenomena. My goal is to investigate these areas and expand them. In terms of applications, in the field of geology, we aim to refine the probabilities of steps and create a general model. We can also implement steps into this model of urban development. In the realm of molecular patterns, we have so far developed our model for materials with hydrogen bonding. Our objective is to estimate the geometry of patterns for other potential types of bonds as well.

 

Publications, references, links

List of corresponding own publications:

[A1] G. Domokos, K. Regős, Á. G. Horváth: A two-vertex theorem for normal tilings. Aequantiones Mathematicae, 97, 185–197 (2023). https://doi.org/10.1007/s00010-022-00888-0

[A2] Domokos, G., Regős, K. A discrete time evolution model for fracture networks. Cent Eur J Oper Res (2022). https://doi.org/10.1007/s10100-022-00838-w

[A3] K. Regős, R. Pawlak, X. Wang, E. Meyer, S. Decurtins, G. Domokos, K. S. Novoselov, S. Liu and U. Aschauer, Polygonal tessellations as predictive models of molecular monolayers, 2023, Proceedings of the National Academy of Sciences, e2300049120, 120, 16, https://doi.org/10.1073/pnas.2300049120

[A4] P. Bálint, G. Domokos, K. Regős, An evolution model for polygonal tessellations as models for crack networks and other natural patterns, https://arxiv.org/abs/2301.09503

[A5] Regős Krisztina – Térkitöltő mintázatok geometriai modelljei, thesis, 2022

 

Table of links:

https://www.quantamagazine.org/the-simple-geometry-that-predicts-molecular-mosaics-20230621/

https://forbes.hu/extra/30per30-2023/#/person/22-regos-krisztina

https://docs.google.com/spreadsheets/d/1DW1-SnQ6rKslPjfJQh0h_aKAJwWXlRcFZcrCqi0fi1E/edit?usp=sharing

 

List of references:

[B1] Gábor Domokos, Zsolt Lángi. On Some Average Properties of Convex Mosaics. Experimental Mathematics, 2019, DOI: https://doi.org/10.1080/10586458.2019.1691090

[B2] Kyparissi-Apostolika, N. (1999). The Palaeolithic deposits of Theopetra Cave in Thessaly (Greece). British School at Athens Studies, 3, 232–239. http://www.jstor.org/stable/40960232

[B3] Domokos, G., Lángi, Z. Plato’s Error and a Mean Field Formula for Convex Mosaics. Axiomathes (2019). https://doi.org/10.1007/s10516-019-09455-w

[B4] https://www.sevenchurches.org/wp-content/uploads/2020/04/Roman-Road-System-Mediterranean-LGC-Wilson.pdf

[B5] Müller, V. (1939). The Origin of Mosaic. Journal of the American Oriental Society, 59(2), 247–250. https://doi.org/10.2307/594065

[B6] Gábor Domokos, Douglas J. Jerolmack, Ferenc Kun, and János Török. Plato's cube and the natural geometry of fragmentation. Proceedings of the National Academy of Sciences, 117(31):18178-18185, 2020.

 

 

 

.