Géza Pattantyús-Ábrahám Doctoral School of Mechanical Engineering 

BME GPK, Department of Building Services and Process Engineering

Supervisor: Dr. HÉGELY László

Multi-objective optimisation of batch distillation methods

Introducing the research area

Distillation is a method for separating liquid mixtures into their components based on differences in their volatilities. It is the most frequent separation method in the chemical industry. However, it is a very energy-intensive process. Also, the specific energy demand of the batch distillation (BD) processes is higher than that of continuous distillation. Therefore, reducing the energy demand and computational intensity of optimization of BD plays a crucial role in improving the sustainability of batch chemical processes.

Brief introduction of the research place

My research takes place at the Department of Building Services and Process Engineering of the Faculty of Mechanical Engineering in the framework of Géza Pattantyús-Ábrahám Doctoral School of Mechanical Engineering Sciences. I work on optimization problems which include analyzing data, writing manuscripts, and collaborating with colleagues. Additionally, for our R&D projects, we utilize the Stokes Laboratory, where we conduct experiments and tests.

History and context of the research

 

Optimization can increase the profitability of BD processes and reduce their energy demand and environmental impact. For the optimization of BD processes, Mujtaba (2004) distinguished three optimization problems: maximum distillate, minimum time, and maximum profit. Minimizing the time also decreases the energy demand. Other objective functions (OF) include the energy demand of the process (Furlonge et al., 1999) or the processing capacity (Nemeth et al., 2020) of the process, as well as environmental indicators such as CO₂ emissions (Wang et al., 2020), global warming and acidification potential (Zhao et al., 2021). Since BD is a dynamic process, a dynamic optimization problem needs to be solved. Adopting the commonly used feasible path approach, the objective function is evaluated by repeatedly solving the model of the process at different points in the space of optimization variables. However, simulation of the process is time-consuming. When a flow-sheet simulator is applied, the optimization is most frequently performed by an external tool using an evolutionary (usually a genetic) algorithm (e.g., Pommier et al., 2008). Genetic algorithms are also commonly applied for multi-objective optimization (Parhi et al., 2020). These methods require a large number of evaluations of the OF, which makes the optimization computationally intensive. Hegely and Lang (2016) maximize the profit of a conventional BD and a batch extractive distillation process by applying a genetic algorithm (GA). Both processes recover methanol from an azeotropic waste solvent mixture containing acetone, tetrahydrofuran (THF), water, and toluene. The production campaign consisted of the regeneration of six batches with off-cuts recycled to the next batch.

To achieve faster optimization compared to evolutionary algorithms, but without losing the ability to find a global optimum, a new surrogate model-based optimization (SMBO) method is proposed here.

The research goals, open questions

 

The research aims to address the energy-intensive nature and computational intensity of the optimization of batch distillation (BD) processes in the chemical industry. The primary goal is to reduce the energy demand and enhance the sustainability of batch chemical processes through optimization techniques.

The proposed method builds upon the work of Hegely and Lang (2016) who optimized the batch distillation treatment of a five-component azeotropic waste solvent mixture using a genetic algorithm (GA). They focused on the optimization of a methanol recovery process by using a genetic algorithm. However, since GA requires a large number of simulations, it is computationally intensive.

To overcome this computational burden, a surrogate model-based method was introduced. Simulations were conducted using a flow-sheet simulator on specific points generated by Latin hypercube sampling in the optimization variable space. From the resulting simulation data, algebraic surrogate models were developed using the ALAMO machine-learning technique. These surrogate models described the objective function (profit of a single batch) and the constraints (purity of the main cut and composition of the second fore-cut).

By utilizing these surrogate models, the optimization problem becomes considerably easier to solve. The research aims to streamline the optimization process, reduce the computational intensity, and improve the efficiency of batch distillation processes. Ultimately, the goal is to achieve optimal operating conditions that maximize the profit from a single batch - while meeting product purity requirements and composition constraints.

 

Methods

The objective function (OF) is the profit from a single batch. It is composed of the price of methanol in the main cut, the costs of incineration of the Fore-cut 1, and of steam consumption during the process (Hegely and Lang, 2016).

The following inequality constraints apply to the optimization problem:

Constraint 1 guarantees the required purity of the product. Constraints 2 and 3 are necessary to prevent organic pollutants C and E from accumulating in Fore-cut 2 so that they can be recycled to the next batch.

First, a large number of test points are generated in the space of the optimization variables using Latin hypercube sampling (LHS). At each point, a simulation is performed by using ChemCad, the results of which are the values of dependent variables needed to calculate OF and the left-hand side of the constraints. In the space of the optimization variables, 500 points are generated using LHS. Within the intervals selected by LHS, the values of the optimization variables are randomly generated. Then, a simulation is performed at each point. The batch distillation process is modeled in ChemCad Version 7.1. Performing the calculations on the original range yields few points with acceptable purity.

Surrogate models are fitted by ALAMO to the simulation results necessary to calculate OF and the left-hand sides of Constraints 2 and 3.

ALAMO fits algebraic models by optimizing a selected criterion describing the goodness of the fit. The models are generated as combinations of previously chosen basis functions, not necessarily used in the final model. Optimization is performed with SQP by using Maple.

Results

The surrogate models accurately described the simulation results (Figure 1). As shown in Figure 1, the surrogate model (surface) was able to predict the mass of Fore-cut 1 (dots) with good accuracy. As R1 increases, mfc₁ decreases at low Cr₁ values but increases slightly at higher Cr1 values. As Cr₁ increases, mfc₁ decreases because Step 1 stops earlier. The profit obtained by the surrogate model-based optimization was 5% higher than the one obtained by Hegely and Lang (2016) by using GA, while the number of simulations decreased from 3000 to 1000.

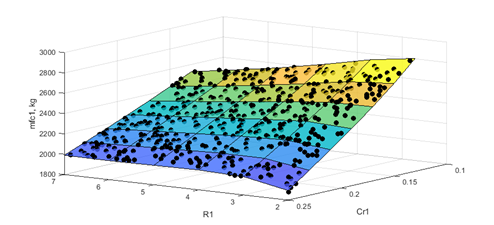
Figure 1: Mass of Fore-cut 1 calculated by simulation (dots) and by the surrogate model fitted (surface).

 

 

Expected impact and further research

 

Although a dynamic optimization problem must be solved first, the method has the advantage that economic data only occur in the profit function; therefore, only the surrogate optimization problem has to be re-solved if cost parameters change. This highlights another advantage of SMBO: in contrast to conventional optimization methods (such as GA), where the process has to be re-optimized if economic data change (Mujtaba and Macchietto, 1993), with SMBO, only the surrogate optimization problem has to be re-solved without any further simulation, provided the surrogate models are chosen appropriately, i.e. they do not contain economic data. This work is among a handful of papers where surrogate models are used for the optimization of batch distillation processes and the first one where they are used for more than two optimization variables. This method can further be applied to other distillation processes where the dynamic optimization problem needs to be solved.

By refining the iterative sampling step, further reduction in the number of simulations can be achieved.

 

Publications, references, links

Journal publications

1. László Hégely, Marton Tamas Szucs, Ömer Faruk Karaman, Peter Lang: Surrogate Model-Based Optimisation of a Batch Distillation Process, Chemical Engineering Research and Design, 192, 456–467, 2023, https://doi.org/10.1016/j.cherd.2023.02.043
2.  László Hégely, Ömer Faruk Karaman, Peter Lang: Improving the Sustainability of Acetone Recovery, Chemical Engineering Transactions, 2023.

Conference publications

1.      László Hégely, Marton Tamas Szucs, Ömer Faruk Karaman, Peter Lang: Optimisation of a Batch Distillation Process by Applying Surrogate Models, 12th International Conference on Distillation& Absorption. Paper: 1242, 2022.

2.   László Hégely, Ömer Faruk Karaman, Peter Lang: Optimisation of Pressure-Swing Distillation of a Maximum-Azeotropic Mixture with the Feed Composition between the Azeotropes, 25th Conference on Process Integration, Modelling and Optimisation for Energy Saving and Pollution Reduction. PRES22.0188, 2022.

 

List of references

1. L. Hegely and P. Lang, Journal of Cleaner Production, 136, 99–110 (2016)

2. Mujtaba, I.M., 2004. Batch distillation: design and operation. Imperial College Press, London, UK.

3. Nemeth, B., Lang, P., Hegely, L., 2020. Optimization of solvent recovery in two batch distillation columns of different sizes, J. Clean. Prod. 275, 122746. https://doi.org/10.1016/j.jclepro.2020.122746.

4. Parhi, S.S., Rangaiah, G.P., Jana, A.K., 2020. Mixed-integer dynamic optimization of conventional and vapor recompressed batch distillation for economic and environmental objectives. Chem. Eng. Res. and Des. 154, 70–85. https://doi.org/10.1016/j.cherd.2019.12.006.

5. Pommier, S., Massebeuf, S., Kotai, B., Lang, P., Olivier, B., Floquet, P., Gerbaud, V., 2008. Heterogeneous batch distillation processes: Real system optimization, Chem. Eng. Process. 47, 408–419. https://doi.org/10.1016/j.cep.2007.01.022.

6. Wang, Y., Yang, X., Zhao, J., Liu, X., Yao, D., Cui, P., Wang, L., Zhu, Z., Li, X., Xu, D., 2020. Design and comprehensive analysis of a novel pressure-swing batch distillation process for the separation of a binary azeotrope with various boiling behaviors. Sep. Purif. Technol. 251, 117329. https://doi.org/10.1016/j.seppur.2020.117329.

7. Zhao, J., Shen, Y., Li, C., Zhao, F., Li, X., Zhu, Z., Wang, Y., Cui, P., Gao, J., 2021a. Sequential two-column batch distillation processes for separation of ternary mixture containing three binary minimum boiling point homoazeotropes. Sep. Purif. Technol. 270, 118826. https://doi.org/10.1016/j.seppur.2021.118826.